立足基础 关注能力 引导教学*
——浅谈2018年南京中考数学试题
2018-08-31庞彦福
☉江 南 大 学 附 属 实 验 中 学 庞彦福
☉江苏省无锡市东绛实验学校(中学部) 陈秋晓
☉山 东 省 肥 城 市 龙 山 中 学 李洪涛
一、试卷的整体情况分析
数学教育教学的目的是使学生掌握必要的数学知识,体悟数学学习过程中的基本思想方法,提升数学能力,增长数学智慧.中考是检测学生几年来在数学学习中获得的知识、能力与智慧,以及学生对数学的理解力、运用力及学习力的有效手段.2018年南京数学中考试题遵循《关于全面深化课程改革,落实立德树人根本任务的意见》的基本要求,体现《义务教育数学课程标准(2011年版)》(以下简称《标准》)的基本理念,充分考查了学生的基础知识和基本技能,注重对学生的数学思想方法、创新意识与实践能力的考查.将数学能力的考查落实在学生层面上体现了“算”与“证”的本质.当然试卷上的“算”并不是死算,而需要有“运”的过程、“计”的方法;“证”是推理,是寻道,是发现.全卷采取多题把关、多题压轴,而且把关的大题切入点适宜,信度、效度、梯度合理,制高点具有挑战性,设问角度新,思辨空间灵动且丰富,能激发学生的好奇心和探究欲,学生的解答过程能够体现出不同层次的数学品质、素养和习惯,具有很好的效度和区分度.同时试题在坚守近几年的命题风格基础上,进行了适度的发展与创新,对知识和能力实现了宽视野、多角度、多层次考查,既考查了初中毕业生学习数学、认识数学的整体理解力,也考查了学生对所掌握基本知识的运用力、思维力,同时又兼顾了高中阶段选拔需要的可持续发展力.在“数与代数”“空间与图形”“统计与概率”等板块设置合理,而且能够将“综合与实践”内容有机融入其中,把“四基”作为命题的重点,从知识技能、数学思考、问题解决、情感态度四个维度进行考查.不像有的试题命制风格是前半部分“送分”后半部分“送命”!整份试卷立意求新,层次分明,亮点纷呈,考查知识覆盖面广,是一份质量较高的考查数学能力的试卷.

表1 试卷考查的知识点分布
二、典型试题赏析
1.低起点,易上手,立足基础
初中阶段数学中的核心知识点是形成数学能力的重要载体和抓手.对学生数学学习的考核与评价首先体现在基础知识、基本技能、基本思想方法和基本活动经验四个方面,注重知识的直接应用.试卷中基础题占的比重较大,约为总量的70%.即使是后面的大题对大部分学生来说还是比较容易上手的.
例1 (第26题)如图1,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F.⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.

图1
赏析:观察图形,对于第(1)问,学生容易上手,先根据“圆内接四边形对角互补”得∠FGD+∠FCD=180°,又由∠FGD+∠AGF=180°,得出∠FCD=∠AGF.再利用“同角的余角相等”得到∠FDC=∠FAG.根据“两角对应相等的两个三角形相似”证得△AFG∽△DFC显得自然合理.尽管是次压轴题,该问绝大多数学生能够拿到分数.第(2)问要求⊙O的半径,如何获得解题思路呢?其实方法较多,现举出两种解题思路.
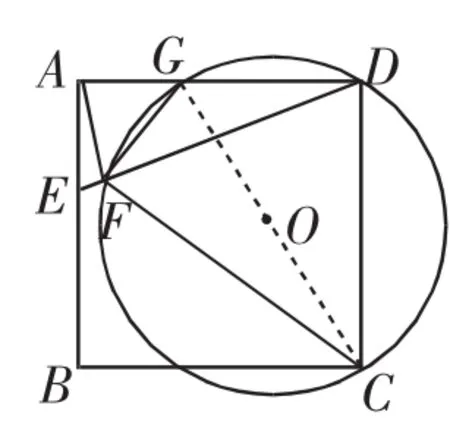
图2
思路二:连接GC,先规避繁琐的运算过程.由“90°的圆周角所对的弦是直径”,可知CG为⊙O的直径,要求半径,只要求出直径CG即可.在Rt△GDC中,已有CD为4,若能出现AG=AE=1,则问题解决.利用(1)△AFG∽△DFC,可得.又易证△AEF∽△DAF(当然也可证明△EDA∽△ADF),则,这样就由AD=DC,得出AG=AE,从而问题得到解决.
解决第(2)问的思路二减少了复杂的运算,但对学生的逻辑推理能力有了更高的要求,这样证明线段相等的思路也是常见的.该题综合考察圆、相似三角形的有关知识.从题目呈现的结构特点看,第(1)问是解决第(2)的基础、“梯子”.有了这样的“梯子”或铺垫就容易拾级而上.
2.高观点,重核心,突出主干
主干知识是中考命题者青睐的对象,在数学的核心知识的交汇处命题,有利于考查学生的数学素养及探究能力,有助于从知识考查走向能力立意.
例2 (第20题)如图3,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.
赏析:识别角的关系、识别特殊平行四边形(菱形),是初中数学的核心知识点,是重要内容.第(1)问,证明两个角相等,结合已知条件中的“∠C=2∠BAD”,可转化至证∠BOD=2∠BAD即可.
如何证明呢?方法是不唯一的.
思路一:题中“OA=OB=OD”属于“定点定长型”,易想到构造圆.点A、B、D是在以点O为圆心、OA为半径的“隐圆”上,如图4.根据“圆周角的度数等于它所对弧上的圆心角度数的一半”即可得到∠BOD=2∠BAD.
思路二:若“心中无圆”,依然容易想到:作AO的延长线OE,如图5.由“三角形的外角等于与它不相邻的两个内角的和”,不难得到∠BOE=2∠BAO,∠DOE=2∠DAO,从而证明出∠BOD=2∠BAD,于是问题得到解决.

图3

图4

图5

图6
第(2)问证明四边形OBCD是菱形.根据菱形的判定定理:四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形.因此,证法1:连接OC,如图6,先证△BOC≌△DOC,得到∠BOC=∠DOC、∠BCO=∠DCO.再根据(1)∠BOD=∠BCD,可得∠BOC=∠DOC=∠BCO=∠DCO.从而得到OB=BC=CD=DO,实现由“四边形”到“菱形”的证明.证法2:若连接OC、BD,由“OB=OD、CB=CD”得OC是BD的垂直平分线,根据“对角线互相垂直的平行四边形是菱形”,从而可以证明.这一过程中,容易忽略是没有先证明出“四边形OBCD是平行四边形”,这是推理过程中不完备的地方.其实,菱形的定义也是识别菱形的方法,“有一组邻边相等的平行四边形叫做菱形”,因此,还可运用证法3:先证四边形OBCD是平行四边形,再找出一组邻边相等.
题目解答方法越多,学生答题时选择的余地就较大,从而就越能考查出学生思维能力、理解能力、思辨能力以及运用数学知识解决问题的能力.
3.识图形,重关联,彰显本质
选拔性考试离不开一定量的难题来实现区分,考试中的所谓难题,目的是将不同层次的学生区分开来.这样的题目在命制和设置的过程中,或是综合性较强,或是运用的知识点较多,或是需要深度的思考与理解.
例3 (第16题)如图7,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′C′D′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为______.

图7

图8
赏析:求圆中的一条弦长,从题目到图形,构图自然、妥帖,为学生所熟悉,考查学生对基本图形的识别和逻辑推理能力.多数学生可能会想到平时学习中常用的解题策略,譬如构造“垂径三角形”.如何构造呢?由条件“相切”自然而然联想到“垂直”,是一种常用的切入方法.连接OE并反向延长交CD′于G,如图8,便可构造出所需要的目标三角形Rt△OGC.由旋转性质可知,CB′=CB=4=EG,由半径OE=OC=CD=,进而求得OG=,再根据勾股定理得出GC=2,然后根据垂径定理求得CF=2CG=4,即为答案.
此题以几何图形的运动——旋转变换为载体,结合矩形、圆和直角三角形,利用几何知识进行推算.作为填空题的压轴题,也是客观题的压轴题,在计算并不复杂的前提下,覆盖知识广泛,较好地考查了学生的综合能力.图形变换的方法,融入数学核心思想方法,突出考查学生的思维过程和数学素养,这种理念与PISA测试的基本思想相吻合.
4.从方程,至函数,厘清推算
方程、函数是刻画现实世界数量关系的有效模型,学习方程、函数,就要会探索简单实例中的数量关系和变化规律,能结合图像对简单实际问题中的函数关系进行分析,用适当的函数表示法(包括图像)刻画简单实际问题中变量之间的关系,结合对函数关系的分析,能对变量的变化情况进行合理讨论,从定性分析到定量刻画.
例4 (第24题)已知二次函数y=2(x-1)(x-m-3)(m为常数).
(1)求证:不论m为何值,该函数的图像与x轴总有公共点;
(2)当m取什么值时,该函数的图像与y轴的交点在x轴的上方?
这个试题立意新颖,构思巧妙,极富创意,蕴含着丰富的数学内涵和思想方法,考查了学生对信息的提取与处理能力、问题的探索与分析能力、模型的建立与选择能力,考查学生对函数本质的理解水平,同时能很好地考查出学生的数学素养和数学基本功.
5.探与思,理中运,孕育过程
《标准》指出:数学课程内容“不仅包括数学的结果,也包括数学结果的形成过程和蕴含的数学思想方法”.数学学习过程是学生在特定的数学目标的指引下,进行数学探究和发现活动的过程.
例5 (第27题)结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图9,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
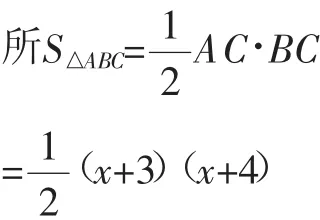


图9
小颖发现“12”恰好就是“3×4”,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若AC·BC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m、n表示△ABC的面积.
赏析:该题考法新颖,贴合学生数学学习的已有经验,考查学生数学学习力,需要学生具有阅读理解能力、迁移能力和创新能力,旨在引导学生主动探究的学习方式,促进学生终生学习能力的发展.第(1)问,特殊问题一般化,不仅能使命题的结构和规律更为清晰,同时又是下面问题的“药引”,肯学习的学生是不难上手的.第(2)问,逆向思考,引导学生合理思辨,探究逆命题的正确性,会学习的学生是能够尝试的.第(3)问,是前两问的升华,既要通过前两问获得猜想结果,又要找出问题的突破口和切入点,善于学习的学生是可以乘胜追击的.通过“问题一般化”“倒过来思考”“条件变式”来完成课题学习.公平合理地考查学生的现场学习能力,引导学生学会解题后的反思,不断积累学习和解题的经验.“授人以鱼,不如授人以渔”,学生在自主学习“方法示范”的基础上,为解题打开思路.解题的过程就是问题转化的过程.
三、教学建议
1.注重基础,凸显数学理解力
学习数学重在理解,理解就必须打好基础.譬如运算往往是许多学生考试中的“关”和“坎”.基础的是基本的、重要的,教与学只有立足基础、夯实基础,才能循序渐进,不断进步与提高.即使是课外拓展与延伸也往往是功在课内,问题在课外,题根在课内.教学中,要特别关注培养和发展学生学习数学的基础知识、基本技能、基本思想、基本活动经验.教学中不能忽略了代数的变形、推算,要夯实运算“童子功”;厘清几何的推证与逻辑关系,要强化推理“命根子”.
2.关注过程,体现数学运用力
让学生体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力.数学思想方法是数学的精髓和灵魂,是学生形成良好认知结构的纽带,是知识转化为能力的桥梁,要在平时的教学中逐步渗透,而且让学生多加体悟,要能够应用到数学学习和问题解决中,在学习中反思,在反思中改进,在学习和应用的过程中不断积累进一步学习的经验.
3.回归本质,彰显数学学习力
学习数学不能单纯依赖记忆与模仿,而需要感悟与思考.注重培养学生的探究能力.重视概念、方法的形成过程,使学生在参与数学活动的过程中理解、巩固、应用和拓展新知,数学素养是一种个人能力,主要体现为“理解数学、运用数学、创新数学”的数学能力.学会用数学的眼光观察现实世界(数学抽象、直观想象)、会用数学的思维思考现实世界(逻辑推理、数学运算)、会用数学的语言表达现实世界(数学建模、数据分析),教学中让学生经历知识的建构过程,突出对数学本质的认识和理解,让学生学会探究,让学生成为善于发现的智慧人.
4.固化知识,提升学生解题力
通过不断思考,让学生在掌握所学知识技能的同时,感悟知识的本质,积累思维和实践的经验.关注学生的合理解题、快速解题.解题教学中要关注学生是怎样获得解题思路的,关注学科本质,注重通性通法.通过解题把握数学本质,体会隐含在其中的数学思想方法,感悟数学的认知结构.解题教学不能以题论题,要培养学生的问题意识,要以知识为载体培养和发展学生数学学习的能力与潜力,以提升学生数学综合素养.
