结构之美 梯度之美 变化之美——2018年重庆市中考数学试题之美赏析

☉重庆市教育科学研究院 张晓斌

☉重庆市永川中学校 唐 芬

《义务教育数学课程标准（2011年版）》（以下简称课程标准）颁布实施后，重庆市于2015年据此全面实施中考内容与形式的改革，现已进入第四年.在课程标准（2011年版）和《2018年重庆市初中毕业学业水平暨普通高中招生考试说明》的引领下，2018年重庆市中考数学试题的命制，继承了2015～2017年的命题指导思想（“求稳，求新”与“四有”：有变化，有广度，有梯度，有厚度），巩固多年的改革成果，很好地实现了“毕业考试”和“高中招生考试”的双重功能.

自2013年以来，重庆市中考试题分A、B两卷，A、B两卷均为同一命题组人员根据课程标准（2011年版）和每年的《考试说明》命题，题型设置、难易度、区分度等均根据同一标准；联招区县使用A卷，非联招区县使用B卷；A卷或B卷系命题时通过抽签决定.据此，本文就A卷试题结构之美、梯度之美、变化之美，以及美之感想进行赏析，以飨读者.

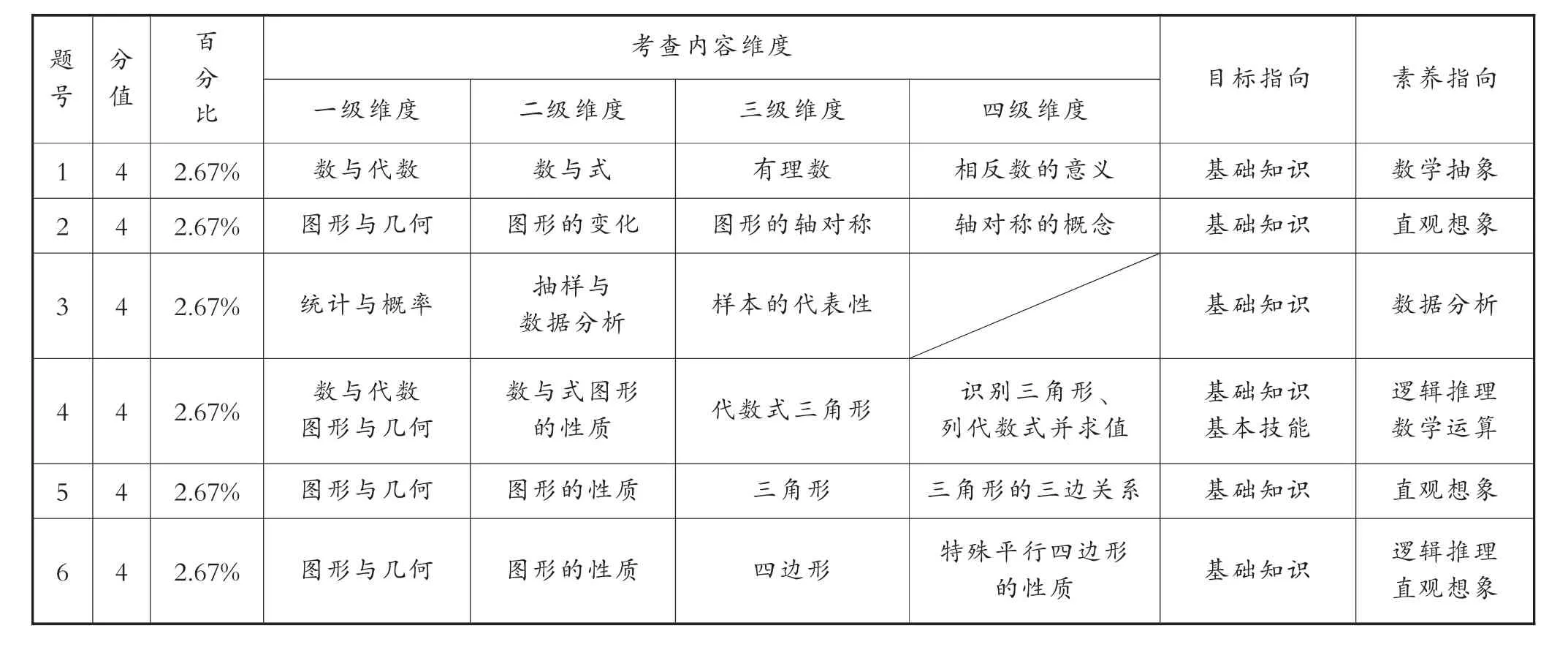
题号考查内容维度目标指向 素养指向一级维度 二级维度 三级维度 四级维度1 4 2.67% 数与代数 数与式 有理数 相反数的意义 基础知识 数学抽象2 4 2.67% 图形与几何 图形的变化 图形的轴对称 轴对称的概念 基础知识 直观想象分值百分比3 4 2.67% 统计与概率 抽样与数据分析 样本的代表性 基础知识 数据分析4 4 2.67% 数与代数图形与几何逻辑推理数学运算5 4 2.67% 图形与几何 图形的性质 三角形 三角形的三边关系 基础知识 直观想象6 4 2.67% 图形与几何 图形的性质 四边形 特殊平行四边形数与式图形的性质 代数式三角形 识别三角形、列代数式并求值基础知识基本技能的性质 基础知识 逻辑推理直观想象

题号考查内容维度目标指向 素养指向一级维度 二级维度 三级维度 四级维度7 4 2.67% 数与代数 数与式 实数 二次根式的运算、估计无理数的大致范围分值百分比数学运算逻辑推理8 4 2.67% 数与代数 数与式 代数式实数 求代数式的值、实数的大小比较基础知识基本技能基础知识基本技能 数学运算9 4 2.67% 图形与几何 图形的性质图形的变化 图形的相似圆 切线、三角形相似的判定和性质 基础知识 逻辑推理直观想象逻辑推理直观想象数学建模11 4 2.67% 数与代数图形与几何10 4 2.67% 图形与几何综合与实践 图形的变化 图形的相似 锐角三角函数、解直角三角形基础知识基本活动经验函数图形的性质 函数四边形 反比例函数、菱形的性质基础知识基本技能数学建模数学运算12 4 2.67% 数与代数 方程与不等式 方程与方程组不等式与不等式组含参数的不等式组、分式方程基础知识基本技能基本思想数学运算逻辑推理13 4 2.67% 数与代数 数与式 实数 绝对值、零指数 基础知识 数学运算14 4 2.67% 图形与几何 图形的性质 四边形圆矩形、扇形的面积 基础知识 数学运算直观想象15 4 2.67% 统计与概率 抽样与数据分析 中位数的概念 基础知识 数据分析16 4 2.67% 图形与几何 图形的变化 图形的轴对称图形的相似轴对称的性质、锐角三角函数基础知识基本活动经验数学建模数学运算17 4 2.67% 数与代数 函数 一次函数 一次函数的综合运用基础知识基本思想基本活动经验逻辑推理数学建模数学建模逻辑推理数学运算19 7 4.67% 图形与几何 图形的性质 点线面角相交线与平行线18 4 2.67% 数与代数 方程与不等式 方程与方程组 一元一次方程、二元一次方程的应用基础知识基本思想基本活动经验角平分线、平行线的性质 基础知识 逻辑推理20 7 4.67% 统计与概率 抽样与数据分析事件的概率条形统计图、扇形统计图、用列表或画树状图求事件的概率基础知识 数据分析21 10 6.67% 数与代数 数与式 整式与分式 整式、分式的加减乘除基础知识基本技能 数学运算22 10 6.67% 数与代数图形与几何函数图形与坐标一次函数坐标与图形运动一次函数的解析式图形的平移基础知识基本思想数学建模数学运算23 10 6.67% 数与代数 方程与不等式 方程与方程组不等式与不等式组24 10 6.67% 图形与几何 图形的性质 三角形四边形一元一次不等式二元一次方程三角形面积、全等平行四边形的性质基础知识基本思想基本活动经验基础知识基本思想数学抽象数学运算数学建模逻辑推理数学运算

题号分值百分比考查内容维度目标指向 素养指向一级维度 二级维度 三级维度 四级维度25 12 8% 数与代数综合与实践26 12 8% 数与代数图形与几何数与式方程与不等式应用意识函数图形的性质图形的变化代数式方程与方程组阅读理解一次函数二次函数三角形四边形图形的轴对称图形的旋转数的整除完全平方数的特征二元一次方程的特解一次函数二次函数三角形菱形图形的翻折和旋转基本思想基本活动经验基础知识基本技能基本思想基本活动经验数学抽象逻辑推理数学运算数学抽象直观想象逻辑推理数学建模数学运算

一、结构之美

2018年的重庆市中考试题依标据本，结构合理，立足基础，覆盖全面.重视对学生“四基”、“四能”和“六素养”的考查，既注重知识的全面性掌握，又凸显重庆考题对有关知识的侧重性青睐.对学生的知识结构、认知结构、素养结构考查系统、全面，试卷的题型结构、难度结构、梯度结构越来越规范统一，淋漓尽致地彰显了数学学科的“结构之美”，具有很好的素养导向性作用，更加明确地指向教师的教、学生的学.

1.考查内容全面，知识结构比例适当，覆盖面广

课程标准一级维度四大板块的课程内容，在本套试卷中都有考查，覆盖率为100%；分值占比合理，数与代数、图形与几何、概率与统计、综合与实践所占分值百分比分别约为47%、38%、10%、5%，与课程内容所占课时比大致相当.

课程标准二级维度八个方面的课程内容，即数与式，方程与不等式，函数，图形的性质，图形的变化，图形与坐标，抽样与数据分析，事件的概率等，在本套试卷中都有考查，覆盖率为100%.

课程标准三级维度的课程内容共37个，除图形的投影、尺规作图、方差、频数没有考查外，其余内容都有涉及，覆盖率达89%.

课程标准四级维度知识点共155个条目，本套试卷涉及其中99个条目中的知识点，覆盖率约64%.

2.考查目标明确，认知结构布局合理，注重学科素养考查

课程标准根据初中学生的认知结构特征，将数学学习的结果目标分为四个层次：了解、理解、掌握、运用；数学学习的过程目标分为三个层次：经历、体验、探索.本套试题对学生认知水平的考查，全面科学，七种认知水平考查分别约占17%、23%、26%、15%、1%、2%、16%，试题的认知水平结构，与课程标准基本一致，对学生四基、四能和核心素养的考核的试题搭配适当，恰到好处.

3.试题形式多样，题型结构平稳优美，搭配合理科学

从全卷看，试题满分150分，考试时间120分钟，共26个试题，客观题约占48%，主观题约占52%.其中，第1～12题是选择题，共48分，约占32%；第13～18题是填空题，共24分，约占16%；第19～26题是解答题，共78分，约占52%.解答题中，题型丰富，有计算题、证明题、作图题、图表信息题、实际应用题、阅读理解题、有“形”无图题等.全卷共22个图形，涉及14个试题，图形与文字相映成趣，相得益彰.

从个体看，多个题目设置多个小问题，几个问题间由易到难，层层递进，前一个问题的答案，可以直接为后一个问题所用，同时为问题的解决提供思考方向和解题思路，体现了试题的结构美.而第26题第（3）问的思维含量较大，解答过程复杂，试卷只要求考生直接写出结果，体现了以生为本的教育理念.

二、梯度之美

整卷试题设置有层次性，难度分布结构适当，坚持低起点、缓坡度，凸显梯度之美.基础题、中档题、较难题之比约为6∶2.5∶1.5.总体难度比2017年有所提高，比2015、2016年略有降低，整卷难度适中，是一套有极好区分度的试卷.

全卷关注到大部分学生的学业水平，注重考查学生的基础知识、基本技能，分值约占60%.其中，单一知识点的试题有第1、2、3、5、6、15题（共计24分），涉及两个知识点的试题有第4、7、8、9、10、13、14、16题（共32分），解答题第19、20、21、22题（共计34分）涉及多个基础的核心知识点，以上题目均系对学生“双基”的考查，大都取之于教材，难度与教材的练习题、习题相当，学生“熟”而不“腻”，可以直接写出答案，或只需简单的计算或者推理即能求解.

本套试卷在注重考查“双基”的同时，还注重对学生基本思想、基本活动经验的考查.第11、12、23、24（1）、25、26（1）题系中档题，约占25%，第17、18、24（2）、26（2）（3）题系较难题，约占15%，对常见的方程、数形结合、分类讨论、函数、换元思想和方法都有涉猎.其中，第10题的综合与实践，第25题的新定义题（阅读理解题），也是对基本活动经验的考查.通过系列具有区分度的试题，很好地实现了中考的选拔和甄别功能.

三、变化之美

纵览全卷，与2015～2017年相比，内容和题型保持相对稳定，保持了2017年已有的变化，如压轴小题第12、17题，几何压轴题第24题，新定义题第25题，其位置、分值、难度都基本不变.在试卷结构比例、个别题目难度系数等方面有所调整，稳中求变，变中求稳，体现“求稳，求新”的命题取向，但2018年中考试题也出现了一些可喜的变化.

第一，最大的变化是试卷总体难度的变化，弥补了2015～2017年试题过难的不足，摒弃2015～2016年试题中过于繁复的计算、过于生涩的文字语言，把17年考题中只涉及一个知识点的容易题数目从10个变为6个，适当增加中档题目的数量，但较难题的数量和分值与2017年相当，是近几年重庆市难度最适中的中考试题，让少数优生有拥抱满分的可能.笔者预测，今年满分人数与去年大致相当，140分以上人数会减少，但要高于2015年和2016年人数，各分数段学生分布会更加合理.

第二，在内容上有两个明显的变化.一是去掉了多年的考点“科学记数法”，增加了“运算程序图”；二是填空题的压轴题第18题，从难度极高的几何计算探究题，变为带有现实背景的应用题.

题1 （中考第8题）按如图1所示的运算程序，能使输出的结果为12的是（ ）.

A.x=3，y=3 B.x=-4，y=-2

C.x=2，y=4 D.x=4，y=2

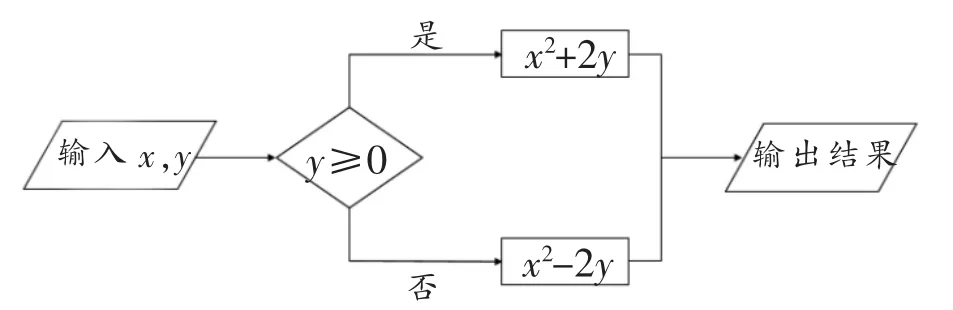
图1

评析：本题考查的知识点为求代数式的值，比较数的大小.根据运算程序，先对输入的y值进行正负判断，再选择对应运算法则进行运算即可.此题尽管简单，但能考查学生的数学运算、逻辑推理能力，具有良好的教学导向作用.

题2 （中考第18题）为实现营养的合理搭配，某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中，甲种粗粮每袋装有3千克A粗粮，1千克B粗粮，1千克C粗粮；乙种粗粮每袋装有1千克A粗粮，2千克B粗粮，2千克C粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中A，B，C三种粗粮的成本价之和.已知A粗粮每千克成本价为6元，甲种粗粮每袋售价为58.5元，利润率为30%，乙种粗粮的利润率为20%.若这两种袋装粗粮的销售利润率达到24%，则该电商销售甲、乙两种袋装粗粮的数量之比是______.

解析：每袋甲种混合粗粮中，A粗粮总成本价为3×6=18元，根据甲的售价、利润率列出等式=30%，可求出甲总成本为45元/袋，则甲中B与C总成本为45-18=27元，故乙中B与C总成本为27×2=54元/袋，乙总成本为54+1×6=60元/袋.设甲销售a袋，乙销售b袋使总利润率为24%，则

评析：本题为商品销售问题，主要考查利润、利润率、成本之间的数量关系，以及不定方程（二元一次方程）的应用，对逻辑推理、数学建模、数学运算素养有较高要求，难度较大.但这与以往第18题大部分考生选择直接放弃相比，本题是学生熟悉的生活背景和数量关系，涉及的知识点是七年级所学，因此学生入手快，起点低，缓坡度.但题目数量多，多达11个，容易导致题意模糊，且运算量较大，这可能会成为大部分考生的拦路虎.因此，这道新题，会比以往的第18题得分率略高，是一道“貌似熟悉，却暗藏玄机”，具有较强区分度，值得推介的好题.

四、美之感想

1.全卷约3000字（不计空格和图表），平均阅读量约为25字/分钟，另有图形22个，这与2015～2017年的中考试题阅读量基本相当，也是重庆考题保持多年的特色.然而全国绝大部分省市中考试题阅读量在20字/分钟以内，相比而言，重庆试题文字、图表阅读信息量偏大，给大部分中等水平的学生，造成了因为文字、图表阅读困难的解题障碍.

的确，对数学核心素养的考查包括在特定情境下应用数学能力的考查，应该考查学生快速阅读、即时提取有效信息、快速判断运用等关键能力，而非做纯粹的数学题.因此，适度的阅读量是需要的，这样才能真正的启迪思维，培养能力，发展素养.但如果过大就会偏离数学学科考查的主旨，毕竟简约美、简洁美是数学的学科特点.

2.重庆今年中考数学试题考查内容、试卷结构、难度系数等都趋于稳定，但极致的稳定会产生“固化”“模式化”倾向.

例如作为选择题的压轴题第12题，近3年都是围绕含字母系数的不等式组、分式方程的解的情况展开，确定待定系数a的值，并求它们的和.

A.10 B.12 C.14 D.16

A.-3 B.-2 C.1 D.2

又如，第17题作为填空题的压轴题之一，近3年均系一次函数图像题，考查的是行程问题中相遇问题或追及问题，横坐标均代表运动时间，纵坐标均代表甲、乙两人（车）之间的距离，结果都是求某种条件下甲距某地的距离.

再如，第23题第（2）小题，是具有重庆“烙印”的含“a%”的应用题.从2016年到2018年，题目背景从2016年的猪肉价格，到2017年的樱桃、枇杷价格，再到2018年的道路硬化、拓宽费用；2016年该题出现“a%”共3次，即猪肉“价格下调a%”、“总销量增加了a%”，“总金额日提高了a%”；2017年该题又出现了3次“m%”，即樱桃“销售量减少了m%”、枇杷“销售量增加了2m%”、枇杷“销售均价减少了m%”；2018年该题甚至出现5次“a%”，即投入经费“增加10a%”，费用“分别增加a%，5a%”，里程数“分别增加5a%，8a%”.虽有题目背景、字母及出现频次变化，但该题考查的核心知识都是一元二次方程，解题思想都是换元，核心素养都是数学建模，求的都是待定字母a（m）的值.

同样具有重庆“烙印”的第25题（阅读理解题），2015年是第23题，新定义“和谐数”，2016年在第24题，新定义“最佳分解”和“吉祥数”，2017年调到第25题，新定义“相异数”，2018年继续保留在第25题，新定义“级数”，这4道题都涉及的内容是新定义“数”、多位整数的表示与整除、完全平方数、求最值等.

我们认为，作为区分度较高的第12、17、23（2）、25题，同一种类型的题目出现1次或者2次是可以的.但近几年多个题目在同一试卷中连续出现3次，甚至4次，考查的基础知识相同，试题形式、分值、难度、位置都基本一致，这种高度的“稳定”，导致试题的难度、信度大大降低，也导致老师和学生步入题海，大量刷题、押题，不利于培养学生的数学思维能力，也不可能发挥好此类题的甄别和选拔功能.

虽美中不足，但瑕不掩瑜.重庆中考数学试题的命制越趋成熟，体现在全面性、选拔性、公平性、创新性等诸多方面，2018年试题更是在结构美、梯度美、变化美等方面得到了充分展现，展示了重庆中考数学命题专家团队的集体智慧.期待未来的重庆中考数学试题能更加关注对数学核心素养、关键能力的考查.