谈“追问”对学生思维发展的作用
2018-08-31江苏省苏州工业园区星湖学校陈书祥
☉江苏省苏州工业园区星湖学校 陈书祥
对某一问题或内容进行一问之后的多次提问能使该问题或内容的本质得到更深刻的挖掘,围绕教学目标设置的一系列问题如果能跟课堂临时生成的问题巧妙穿插和整合,学生在由浅入深、由此及彼的多次提问下必然能产生更多丰富而深刻的体会和感悟.
一、追问能唤醒思维对话的激情
平等、开放、自由、民主的对话往往能给学生带来美感和情趣并激发出思维上的新意与遐想,教师有的放矢的有效追问往往能令这一对话得到拓展与延伸并使其上升到更高的层面.
案例1 3位教师带领学校科技小组的学生去国家森林公园考察并采集标本.当地的甲、乙两家旅行社在定价上是一致的,不过两家旅行社在优惠政策上各有不同.甲旅行社能帮教师免费并给学生八折的优惠,乙旅行社则可以给教师与学生统一七折的优惠.优惠政策虽有不同,但核算下来的经费都是一样的,那么这一科技小组的学生成员有多少呢?
(这是七年级数学下册中要求学生在课前完成的一个实践与探索的练习)
师:哪位同学能将你的解法到黑板前来展示一下呢?
生1:解:设科技小组学生成员x名,甲乙旅行社的定价是“1”,则80%x=70%(x+3),得x=21.
师:对吗?
生:对的!
师:如果科技组要扩招,大家觉得报哪家旅行社更加划算呢?
生2:试算以后发现乙旅行社还是比较划算的.当科技小组增加1人时,甲:80%(21+1)=17.6;乙:70%(3+21+1)=17.5.选乙旅行社来的划算一些.
生3:我也觉得乙旅行社更加划算,我试了20人嘞.
师:大家以为他们的选择对吗?
生:对的!
师:以上两位同学运用试算的方法进行了选择,但是如果人数增加很多,比如增加到200个,会不会有什么不同呢?大家可有其他看法呢?
生4:我没有那样试算,但我的选择是一样的,我觉得增加的都是学生,两家旅行社给学生优惠,一个是8折,一个是7折,必然应该选乙啊.
(学生讶异之余不禁惊叹:“太棒了!”)
师:大家觉得这一说法怎么样?
生:非常有说服力!
师:学生人数应该在什么范围内选择甲旅行社时比较划算呢?其他条件不作改变.
生:少于21人时,还是选择甲比较划算.
师:如果只有2个老师去了,优惠政策不变,情况会有变化吗?
(学生讨论的气氛越来越热烈)
师:大家都来谈谈自己的见解吧!
生5:我列方程算出了实际收费一致时的情况,然后对其余情况进行了讨论.
(这一少见的解法是那么令人觉得突然)
师:这个想法很与众不同啊,到底对不对呢?老师需要大家的帮助啦,你们真棒,敢于挑战传统,或者还有其他想法吗?
生7:有的.设学生x名,单价为“1”.选甲的话,即80%x<70%(x+2),则x<14;如选甲乙一样,则80%x=70%(x+2),x=14;选乙的话,则80%x>70%(x+2),即x>14.
师:大家是不是觉得这一解法很惊奇,这位同学刚刚参加过数学竞赛,其他同学对其中的不等式还没有学过,有兴趣的同学可以在课后继续探究.大家在课后探究中可以关注以下问题:该同学提出的比例式成立吗?大家能否编写出类似的问题?请大家尝试编写与今天例题相似的题目并进行解决.
二、追问能唤醒已有的个体知识
知识不经过个体的认知与加工将很难内化成个体的观点与思考,有效的追问能促进学生在知识的探索中形成独特的经历、探究与体验并将其沉睡的个体知识真正唤醒.
案例2 三角形的概念.
师:老师给大家展示一组图片(图片略),大家是否觉得其中都包含某种平面几何图形呢?
生:三角形.
师:对!
教师投影图1并提问:什么叫三角形?生1:三角形就是三条线段组成的图形.
师:大家可有不同想法?
生2:不对,按照他说的,我画两幅图,大家看看这是不是三角形呢(画出图2、图3)?所以三角形应该是由三条线段首尾依次连接而组成的图形.
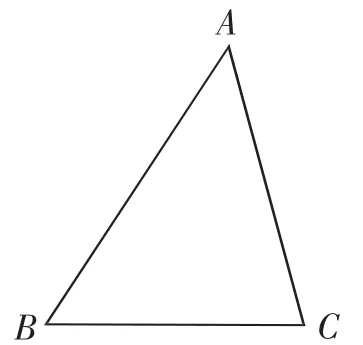
图1
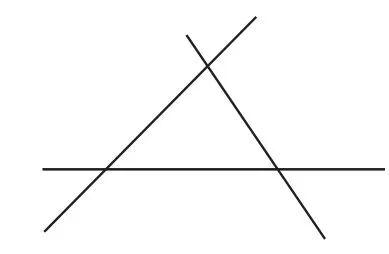
图2

图3
师:大家说对吗?
生3:还是不对,应该再加上“不在同一直线上”这一条件才对,要不然形成的图形有可能只是线段.
该生边说边画出了图4中的线段.
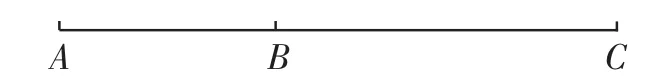
图4
师:太好了!那么大家来讲讲到底什么是三角形呢?
生:三角形就是不在同一直线上的三条线段首尾依次连接而组成的图形.
师:图形中的“角”“垂直”是用“∠”“⊥”这些符号来表示的,大家可知道三角形的表示方法?
生:一个小的三角形图形.
师:大家怎么会知道的呢?
生:“∠”“⊥”这些图形都很形象,我们是受到启发了.
师:很好,同学们不知不觉运用到了类比这一考虑问题的方法,类比一般会从两个或多个事物的相同或相似之处入手并进行其他方面可能存在的相同或相似的推断,它在数学学习中运用得相当广泛.图1中的三条线段可以分别记作线段AB、BC、CA,三个角分别记作∠ABC、∠BAC、∠ACB,大家再运用类比的方法来说说图1中的三角形应该怎样用符号表示吧?
生4:记作“△ABC”.
师:记作“△BAC”“△CAB”可以吗?
(学生陷入讨论中)
生5:不能,∠ABC、∠BAC等表示的都是不同的角,我觉得记作“△BAC”“△CAB”是不对的.
生6:我觉得可以,A、B、C三个顶点在该三角形中的地位应该是一样的,顺序变化不影响它的意义.
师:太好了!由此可见,类比得到的结论也不一定就是完全正确而可靠的,同学们运用类比方法时应仔细斟酌.那么大家认为“△ABC”应该怎么读呢?
生:读作三角形A、B、C.
三、追问能促进思维发展
思维只有在不断挑战与被挑战中才能展现出最大的活力,追问则能将思维的深度和广度不断拓展并有效培养学生思维的深刻性和敏捷性.
案例3 有理数的加法运算法则.
师:足球比赛中将进球与失球分别记作正数与负数,两者之和称为净胜球.红队、蓝队在比赛中分别进4球失2球、进1球失1球,大家觉得两队净胜球数应该怎样计算呢?
生:红队:4+(-2);蓝队:1+(-1).
师:很好,负数出现在了加法中,这就是今天我们要研究的内容.
师:一只蜗牛在数轴的原点:(1)向右爬行5m稍作停留后继续向右爬行了3m;(2)向左爬行5m稍作停留后继续向左爬行了3m;(3)向右爬行5m后又向左爬行了3m;(4)向右爬行3m后又向左爬行了5m;(5)向右爬行5m后又向左爬行了5m;(6)向左爬行5m后又向右爬行了5m;(7)第1分钟向右爬行5m,第2分钟在原地逗留;(8)第1分钟向左爬行5m,第2分钟在原地逗留.大家分别表示一下蜗牛在这八种情况下爬行的结果与运动情况吧.
生1:(1)5+3=8;(2)5+3=8;(3)5-3=2;(4)5-3=2;(5)5-5=0;(6)5-5=0;(7)5+0=5;(8)5+0=5.
生2:这样写有点不妥,虽然结果都是对的,但蜗牛的运动情况未能在算式中表达出来.
师:那怎么办呢?
生3:将蜗牛向右爬行记作正方向,向左则为负,列式如下:(1)(+5)+(+3)=+8;(2)(-5)+(-3)=-8;(3)(+5)+(-3)=+2;(4)(+3)+(-5)=-2;(5)(+5)+(-5)=0;(6)(-5)+(+5)=0;(7)(+5)+0=+5;(8)(-5)+0=-5.
师:大家能用语言文字描述加数的绝对值与和的绝对值之间存在怎样的关系吗?
生4:(1)(2)两式中和与加数的符号相同,因此两者绝对值相等;(3)(4)两式中和与其中一个加数的符号一致,和的绝对值与加数的绝对值的差相等;(5)(6)两式中和的绝对值与加数的绝对值之差相等;(7)(8)两式中和的绝对值分别与非负数加数之和、非正数加数之和的绝对值相等.
师:大家可有更加准确精炼的表达?
生5:看较大加数减较小加数的绝对值.
生6:和的符号和绝对值较大的加数的符号保持一致.
师:接下来我们把这几个式子总结分析一下.
生7:(1)(2)式是同号相加,符号一致,和的绝对值与加数绝对值之和相等;(3)(4)式是异号相加,和的符号和绝对值较大的加数保持一致,和的绝对值与加数的绝对值的差相等;(5)(6)结果是0,两加数互为相反数;(7)(8)式中的加数与零相加仍等于这个数,一共可以分成四类.
师:很好,这就是我们今天要研究的加法运算法则.
课堂教学中的有效追问是教师教学智慧与教学艺术的体现,教师在实际教学中应适时捕捉学生反馈并进行高质量的追问,开启学生智慧的同时演绎课堂教学的精彩.H
