“伪函数”考题的命题商榷与教学应对
——由一道中考题说起
2018-08-31江苏省苏州市觅渡中学
☉江苏省苏州市觅渡中学 庄 严
2018年中考试卷陆续出来,我们对一些地区的中考试题进行了演算、研习,发现了很多精彩的好题(呈现简洁,方法多样,易进难出,有数学味,很好的教学导向),然而还有一些地区仍然延续着一些不好的命题方向,比如在不少期刊上被批判的伪函数题、伪抛物线题.本文选取一例,解析思路,并根据个人喜好给出一些意见和教学建议,供同行批判研讨.
一、考题及思路突破
考题 (2018年S省D市,第25题)如图1,在平面直角坐标系中,直线y=x-1与抛物线y=-x2+bx+c交于A,B两点,其中A(m,0),B(4,n).该抛物线与y轴交于点C,与x轴交于另一点D.
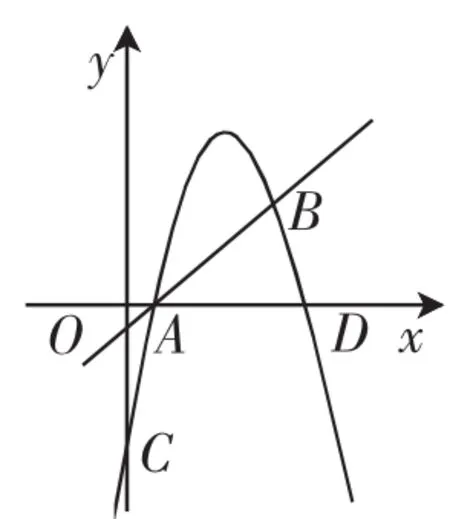
图1
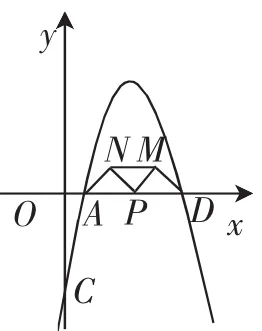
图2
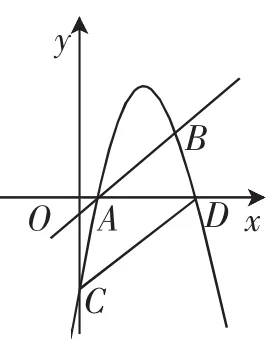
图3
(1)求m,n的值及该抛物线的解析式.
(2)如图2,若点P为线段AD上的一动点(不与A,D重合).分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APN和等腰直角△DPM,连接MN,试确定△MPN面积最大时P点的坐标.
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A,D,Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
思路突破:(1)把A(m,0),B(4,n)代入y=x-1可求出m=1,n=3,再把点A(1,0),B(4,3)坐标代入y=-x2+bx+c中,得方程组所以y=-x2+6x-5.
(2)由上一问已明确的抛物线解析式y=-x2+6x-5,令-x2+6x-5=0,解出x=1或x=5,即D(5,0),结合上一问已有的点A(1,0),接下来的问题就与抛物线无关了,删减无关线条,如图4,只保留△APN与△DPM,均为等腰直角三角形,AD=5-1=4.
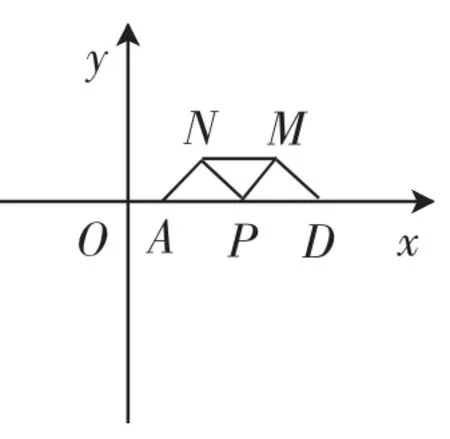
图4
(3)这个小问仍然与抛物线无关,删除抛物线对问题的干扰,构造图5进行分析.
先分析出∠BAD=∠ADC=45°,接下来只要分两种情况讨论:
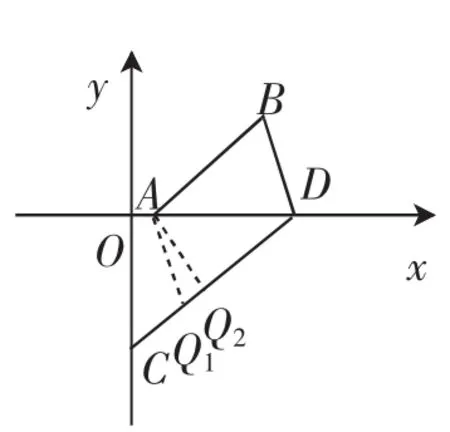
图5
解后反思:从我们给出的思路突破来看,在第(1)问求出抛物线解析式之后,抛物线就退出后续问题的探究,反而成为干扰问题研究的无关线条,是一道伪函数图像问题.以下就针对伪函数问题给出进一步的命题商榷与教学建议.
二、命题商榷与教学建议
第一,地区命题组使命光荣、责任重大,要关注命题研究最新进展
当前我国中考命题多以地级市为命题单位,地市教育局具体组织命题工作,然而由于中考保密的安全责任第一的原则,各地中考命题组成员多以临时抽调为主,缺少系统、专业的命题培训.临时组成的命题组成员(特别是命题组长)如果善于钻研,在命题研究领域有自主钻研,则还能端正命题心态,在理解数学、理解教学、理解学生的基础上主持开展好命题工作;如果眼光有限,对初中数学的理解没有达到深刻理解的高度,则容易随波逐流,抱着稳字当前的心态,以“维稳压倒一切”的指导思想,不求有功,但求无过,八股化学习模仿本地区前几年的考查题型、考查重点.这样下来,如果本地区历来喜好考查所谓的伪函数综合题,则往往又会出现在新一年的中考试卷中,想来这类考题的“生成”大致如此.就近五年来的命题研究进展来看,很多有识之士已对伪函数问题进行过批判和商榷,全国各地几百套的中考试卷中,这类问题也越来越少.像上文中的一道压轴题仍然出现这类伪函数考题现象,实在让人遗憾.
第二,广大备考师生要注意关注地区命题风格,有针对性的备考
中考命题不只承担了评价、区分与选拔功能,更重要的是还有对地区教学引领的重要功能.像上文这样设计这类中考压轴题、把关题,必然导向着地区新一届毕业班的周练、月考、期中期末考、中考模考.“人在屋檐下,不得不低头.”广大备考师生就需要认真研究和关注地区命题风格与命题特点,而不是到全国其他地区盲目选题.像本地区近五年来从没有在最后大题的位置安排所谓“新定义考题”(比如北京卷),就不宜在复习过程中大量选择这类问题进行训练,即使遇到新定义考题,也要有的放矢地进行取舍.毕竟毕业年级师生的精力有限.在这个意义上说,命题对教学导向、对地区师生复习与教学的用力点都起着十分重要的引导作用.
第三,对伪函数问题教学时要引导学生排除干扰,善于“目标解析”
对于伪函数问题的教学是一个现实问题,因为不止是中考试卷的现实引导,各种教辅资料上更是题海战术,大量的伪函数问题出现在教辅资料中,而且不少自媒体公众号也对这类考题“不加选择”地传播,乐此不疲.这时教师在教学这类伪坐标系考题时,要善于引导学生排除干扰,学会开展“目标解析”.比如我们在上文思路解析时,帮助学生分离出来的图4、图5,就是一种问题突显、目标解析,让学生想清此问真正的求解目标、求解方向是什么?方向不明,切勿乱动.很多学生在面对这类较难题出错或浪费时间的根源就是问题还没真正读懂,连解题的目标没有想清,方向走偏,对如惜时如金的考场解题来说,方向不明,不如不做.
三、基于“三个理解”提升中考命题质量
贺信淳老师曾在文3中表达了对初中数学教学现状之惑,既有对伪坐标系的批判(比如这种考题本质上平面直角坐标系搭台、平面几何唱戏),又对这类现象进行了剖析,值得我们倾听和改进.我们认为,破解这种命题现象的关键在于落实章建跃博士提出的“三个理解”.以下就是关于“三个理解”在命题中的一些具体解读:
因为对数学理解得不够深刻,就容易编造出这类伪函数问题.比如,数学中引出平面直角坐标系主要是为了研究函数图像服务,而不是为了研究平面几何中的一些模型或平几中的奇异性质.想清楚这些,如果想考查相似三角形的分类讨论,就可以在平几的基础图形上进行探究,而不必与无甚关联的函数图像进行联系,因为函数的本质是研究图像与性质(特别是增减性).
再有,因为对学生理解(学情理解)得不够深刻,有些命题人员根据自己对某一道习题的钻研成果不经过充分论证就放置在考卷的关键位置,这是值得商榷的,有些习题钻研的心得、性质、成果,并不一定适合直接放在考卷上进行考查,因为考生整场考试要做的题很多,绝大多数考生是没有足够时间来挑战、思考这类超难题的.
还有,如果命题人员能深刻“理解教学”,有些试题就不宜放在中考试卷中,比如解答题中有些“直接写出答案”的设问,就是一种不当设问,既是与解答题题型的要求矛盾,更多的是命题组也想“偷懒”,不给出参考答案和详细过程.另外,如果命题人员认真思考伪函数题对教学的不良导向,也许在命题时就会慎之又慎了吧.
