构建变量关系 理解“函数”特征

☉山东省临沂沂堂中学 赵晓光

开学之初学校安排各年级各学科都要做一次学科打磨课的教研活动.作为一名数学青年教师代表自然责无旁贷地领旨挂帅，作了一节关于《一次函数》的教研课.课后我多次观看当时的课堂场景，与听课教师进行交流，希望自己能够快速成长起来，成为课堂教学的佼佼者.我深知数学课堂活动，是师生之间、学生之间交往互动与共同发展的过程.需要以学情出发，创设一个激发学生自主学习的质疑情境，在唤醒欲望的过程中存疑、解疑、释疑.本次教研课我推陈出新，一改以往给学生大量的探究题，并要求学生快速释疑的低效做法，而选择新方式来讲课.为此，我将创设的探究用PPT形式一一展示出来，并采用自主思考和小组交流等多种活动来存疑、解疑、释疑.在学生的探究活动中做好引导和疏通，答疑和点拨.

一、课堂案例实录

用电子白板展示：

探究1：去超市买桶装方便面，单价为4元/桶，所要购买的数量为t桶，所用总费用为f元.

（1）填写相关表格.

t/桶 1 2 3 … n f/元 …

（2）试用含t的式子表示f.

师：哪位同学愿意在电子白板上填写这个表格？

（生甲举手，被允许后上台填写表格中的数据）

师：你怎么算出来的？

生甲：总费用=价格×桶数.

师：如何用含t的代数式表示f呢？

生甲：f=4t（学生板书出来）.

师：（示意学生回到自己座位上）请同学观察上面等式哪些量在变，哪些量没有变？

生：总费用f、数量t在变，单价没变.

师：总费用随数量的变化而变化.

用电子白板展示：

探究2：学生食堂每份饭的售价12元，如果早餐售出1800份，午餐售出2700份，晚餐售出3090份，三餐食堂收入各多少元？若设一餐售出x份，食堂收入为y元，怎样用含x的式子表示y？

学生开始思考、演算.演算结束.

师：请乙同学来通过投影展示演算结果.

生乙：早餐食堂收入为12×1800=21600元；

午餐食堂收入为12×2700=32400元；

晚餐食堂收入为12×3090=37080元.

式子表示：y=12x.

师：请同学观察上面等式中哪些量在变，哪些量没有变？

生：x、y在变，食堂每份饭的售价12元没变.

师：食堂收入随售出饭的份数的变化而变化.

用电子白板展示：

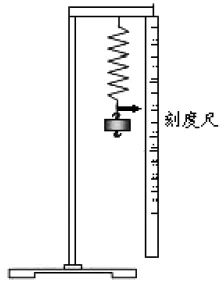
探究3：从物理实验室找来一根50mm的弹簧，再找来一把刻度尺，作一个物理实验（装置如下图），在弹簧的下端挂相同质量的钩码，逐渐增加钩码数量，观察弹簧长度，记录随钩码数量的变化：

钩码数量x/个 0 1 2 3 4弹簧长度L/mm 50

怎样用含钩码数量x（个）的式子表示受力后的弹簧长度L（mm）？

布置任务，让学习小组A三名学生上台演示实验.小组分工：生丙挂钩码、生丁读刻度尺读数、生戊记录填表.

师：戊同学请你来说说填表的情况.

生戊：回答填表情况：

钩码数量x/个 0 1 2 3 4弹簧长度L/mm 50 58 66 74 82

师：请小组根据相关数据分析，用含钩码数量x（个）的式子表示受力后的弹簧长度L（mm），怎么考虑的？

生丙：每增加一个钩码使弹簧伸长8mm，挂了x个钩码，受力后的弹簧长度便伸长8x，弹簧长原长为50mm，所以受力后的弹簧长度L=50+8x.（班级学生鼓掌）

师：回答很好，大家都能分清楚式子中的什么量在变化了吧？

学生：式子中的x、L在变.

用电子白板展示：

探究4：用80cm长的绳子围成长方形，通过改变长方形的长和宽，计算所得到的长方形的面积怎样变化？完成下列数表：

长/cm 35 30 25 20 15 10宽/cm面积/cm2

若长方形的边长为ycm，面积为Scm2，则用含y的式子表示S为_______________.

教学活动过程略去.

在教师的指导下学生根据以上创设的4个探究对其作出的关系式进行归纳：

（1）什么是变量，其主要特征与含义是什么？

（2）常量的特征与含义又是什么？

……

二、课后交流与反思

再次观看自己授课的录像，在备课组教师的交流切磋中深深感悟到了这样的几点不足：

1.在创设探究环境时，很多是自己的一厢情愿，没有抓住学生的实际情况，例如，探究1和2都是以买与卖的材料为载体，雷同的材料不足以拓宽学生视野，备课组成员认为应该更换材料.

2.课堂采用了问题驱动式的讲课方式，形式上对探究学生释疑不拖泥带水，探究本身是否足够深刻，能否唤醒学生的思维？这是课后交流时一些教师提出了的.还有教师提出：学生在课堂上探究、发现、总结规律的过程中，总是让个别或者少数的学生来回答，有些像一言堂.尽管得出变量、常量概念是学生自己总结出来的，很多是学生看书而已，探究是否只成了部分好学生的戏台？

3.还有教师认为：教师作为指导者，培养学生的数学思维能力不能仅仅依靠探究的情景，更多地要注入教师的心血.要让学生学会思考、能够思考，在探究2的问题突破时，给学生不到3分钟的时间，很多学生的表格都没有完成，数值计算也过于“庞大”，应该减小数值的运算量，探究的目的是让学生明确变量和常量，大量的数值运算使得本末倒置.探究3是物理方面的问题，尽管是学生自己动手操作的，而且是合作探究的，但下面的学生只是观望，还有学生纠结在弹簧长度是否可以任意伸长等方面，离开了创设情境的初衷.

4.也有教师认为，课堂用了大量的时间来铺垫变量与常量，是否有些得不偿失.为什么没有对探究进行延伸，比如说加入函数的定义、用方程组的观点解决探究4，等等.还有就是本节课只谈了变量、常量的数值关系，没有涉及单位问题，变量的取值范围问题等.

和众教师30多分钟的交流虽然短暂，但其尖锐、一针见血地指出存在的问题是刻骨铭心的.借助他人的意见或建议，我重新调整了本节内容的解决方法：

1.将探究1留给学生课前作，让导学案前置，起着预热的作用.

2.将探究2换一种背景材料，替换成水池加水或者是高铁行驶之类的背景材料，也让学生在课前完成，课堂上开门见山地提出问题：“在探究1和探究2中，自己在解决问题的过程中，观察到了什么吗？请四位学生上台写出自己的见解.”这样就可以直接得出：①每一个式子中都有两个量可以变化，有不变的数值；②其中一个量改变，另一个量也会随着改变；③当一个量给出一个数值时，另一个量的数值也是一定的，等等.

3.探究3是学生动手实验的，但观望的学生太多，将学生分组，弹簧改为橡皮筋来做实验，让学生全员动手，组与组之间竞争，掀起课堂探究的高潮.尽管各组得出的表格中的数值不同，其最终的表达式也不同，但规律是相同的.再通过小组展示小组实验结果、得出的关系式，让全班学生议一议、评一评强化记忆.

4.在本节课之末，尝试让学生仔细观察生活中的现象编制一道题，从而深化对变量和常量的理解.

三、写在最后

再次讲授打磨后的课的时候显得轻松自然，课堂气氛高涨而和谐.变量与常量是函数的基础，升华为生生不息的运动变化规律中体现出来的重要数学模型——自变量与函数.从变量与常量的角度思考更多的是数学中定量地描述数与形的对应关系.所以，本节课关键所在是构建概念，一个函数初步的概念.在课堂教学中是不能仅仅着眼于具体探究情境的释疑过程，还要不断将具体情境中的相关数学思想抽象化，从整体上认识“函数”的本质.函数是数学的基本思想，需要通过一定材料的载体来体现，学生对数学思想的认识是一个漫长的过程，既需要领悟教材的内容，也需要教师恰如其分的点拨，更需要学生在积极的探究过程中亲身经历和感悟.

总而言之，在教学中需要注重实践，更需要同行们的帮助和交流，通过教研活动可以让教师获得新生、走向成熟.P