深入才能浅出:一类求参数取值范围试题的解析①
2018-08-30李昌成杨军
李昌成 杨军
(1.新疆乌鲁木齐市第八中学 830002;2.新疆师范大学数学科学学院 830054)
1 问题的提出
2017全国高考数学Ⅱ卷文科第21题第(Ⅱ)问(例1)是一道求参数取值范围问题:
例1设函数f(x)=(1-x2)ex.当x≥0时,f(x)≤ax+1,求a的取值范围.
求解例1的方法之一是“分离参数法”,但分离参数后求对应函数的最值时,运算非常复杂(有兴趣的读者可尝试之).而该高考试题所附参考答案的解法,不易理解掌握.同时所见一些解法仍未能体现其源流,故本文以2017全国高考数学Ⅱ卷文科第21题和2016年四川高考数学理科第21题第(Ⅱ)问为例,拟深入分析“当x∈(m,n)时,f(x)≤ax+b恒成立,求a的取值范围”这类试题的本质,并据此给出适于高中生认知水平的初等解法.
2 试题的本质分析
从几何意义看,要使x∈[0,+∞),f(x)≤ax+1成立,只需当x∈[0,+∞)时,射线y=ax+1始终在函数f(x)=(1-x2)ex图象的上方(仅在端点x=0处重合,如图1).进一步发现,直线y=ax+1位于曲线f(x)的切线位置是f(x)≤ax+1成立的极限情形:即若射线y=ax+1(x∈[0,+∞))位于切线位置或其上方时,均有f(x)≤ax+1;若射线y=ax+1(x∈[0,+∞))位于切线位置下方时,f(x)≤ax+1不恒成立(图2).
之所以如此,关键原因是f(x)=(1-x2)ex在x∈[0,+∞)上是凸函数(即曲线是凸的).如若不然,则不能保证“当射线y=ax+1(x∈[0,+∞))位于切线位置或其上方时,均有f(x)≤ax+1”.例如图3中的反例.
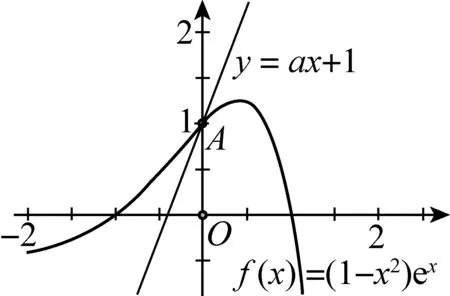
图1
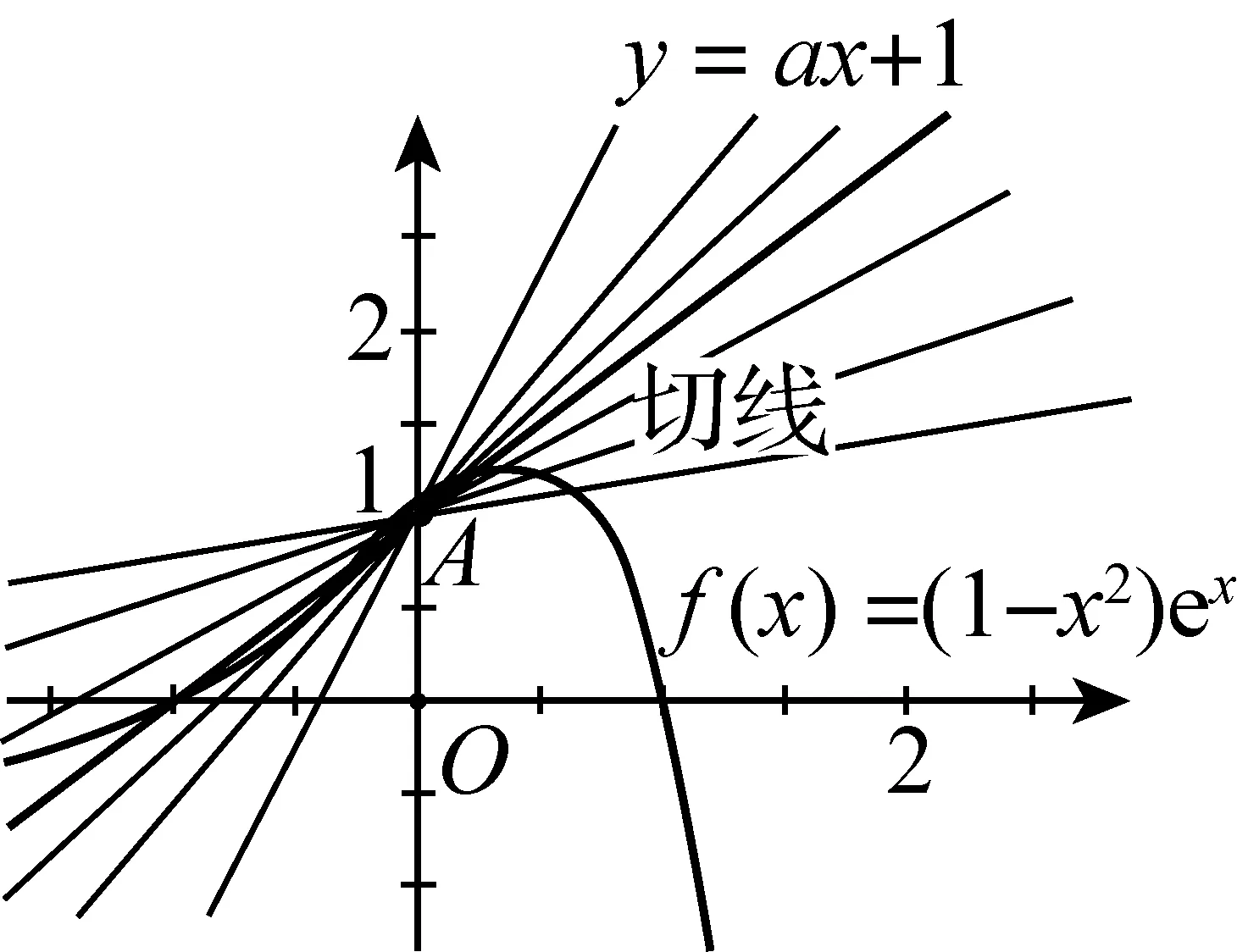
图2
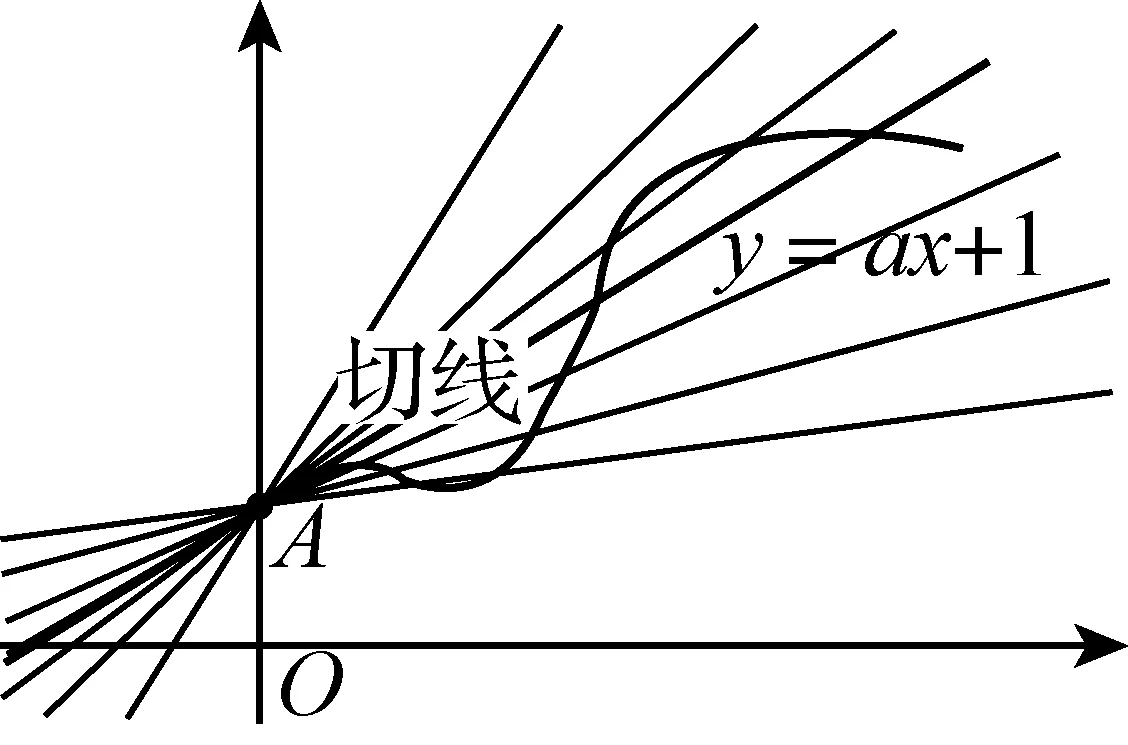
图3
至此,揭示了试题的本质:因为f(x)=(1-x2)ex在x∈[0,+∞)上是凸函数,故条件“x≥0时,f(x)≤ax+1”等价于“射线y=ax+1(x∈[0,+∞))位于曲线f(x)=(1-x2)ex在点x=0处的切线位置或其上方”.
一般地,若函数f(x)在x∈[m,n]上是凸函数,并且函数y=f(x)与y=ax+b在区间[m,n]左(或右)端点处的函数值相等,则“当x∈[m,n]时,f(x)≤ax+b成立”等价于“y=ax+b(x∈[m,n])位于曲线y=f(x)在端点处的切线位置或其上方”(图4).
同理,若函数f(x)在x∈[m,n]上是凹函数,并且函数y=f(x)与y=ax+b在区间[m,n]左(或右)端点处的函数值相等,则“当x∈[m,n]时,f(x)≥ax+b成立”等价于“y=ax+b(x∈[m,n])位于曲线y=f(x)在端点处的切线位置或其下方”(图5).
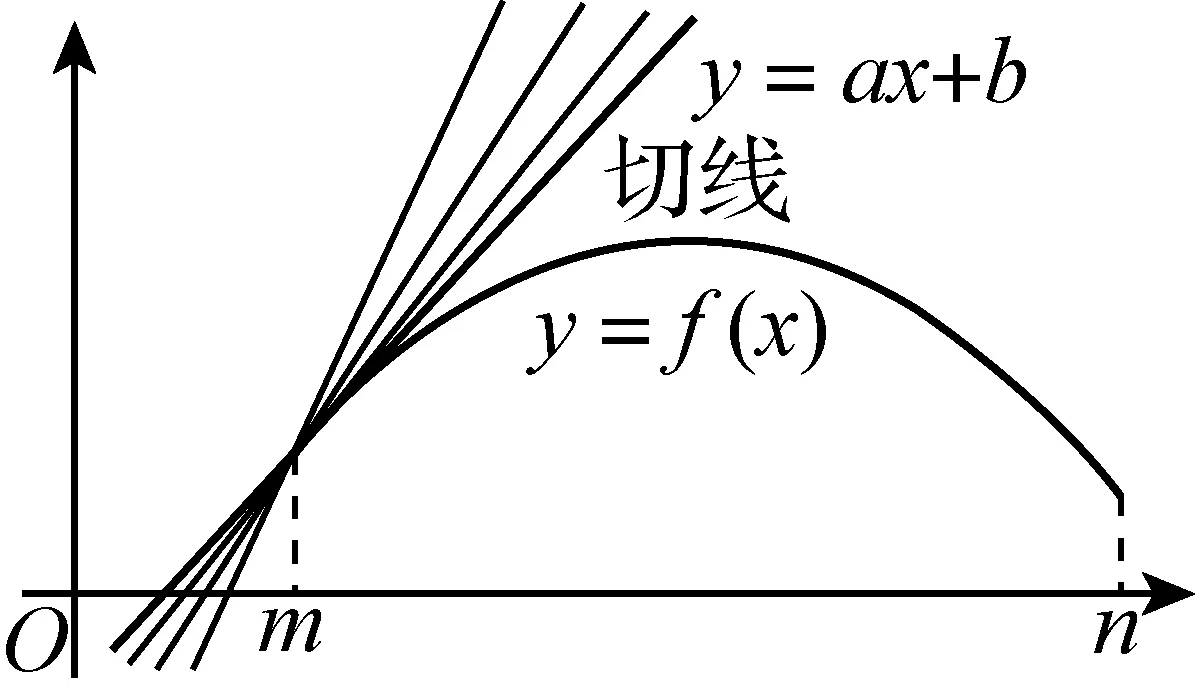
图4
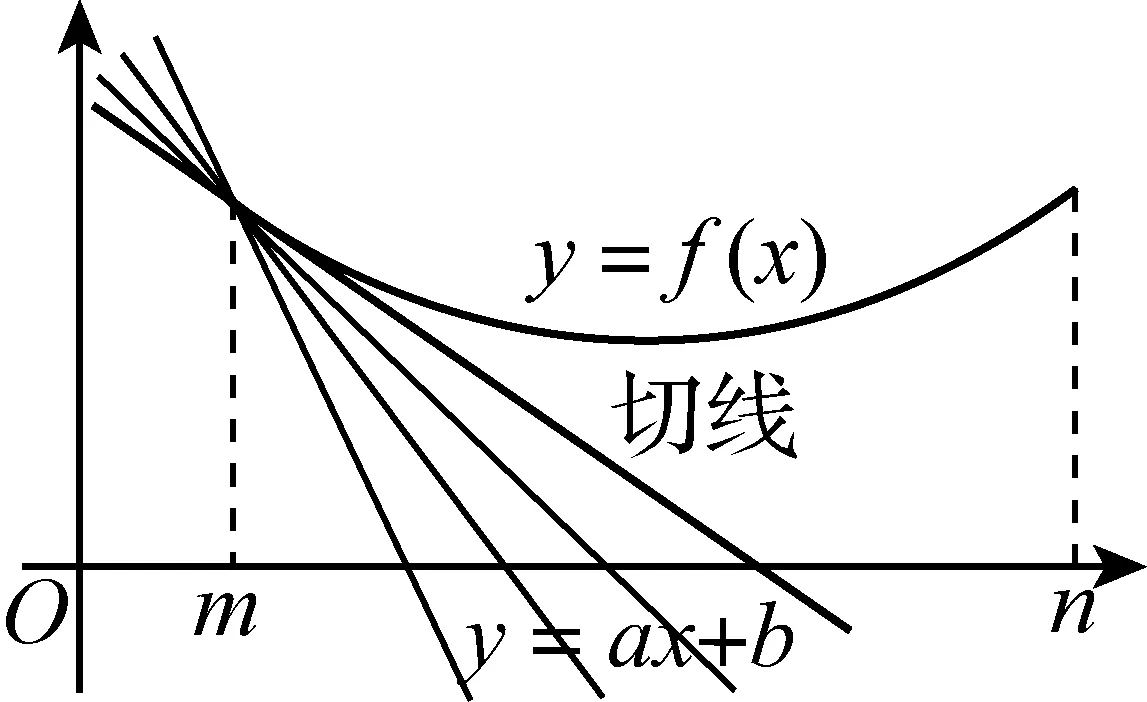
图5
从而,要求参数a的取值范围,只需判断函数y=f(x)在某一区间上的凹凸性,并求出曲线y=f(x)在区间端点处的切线方程,进而根据“y=ax+b(x∈[m,n])位于曲线y=f(x)在端点处的切线位置或其上(下)方”即可求出目标参数的取值范围.从而表明,此类试题是基于函数的凹凸性命制的.
3 基于函数凹凸性的高观点解法
根据以上分析,下面给出例1基于函数凹凸性的高观点解法.其中用到高等数学中判断函数凹凸性的方法如下[2]:
∀x∈I,若二阶导数f″(x)<0,则函数f(x)是区间I上的凸函数;若二阶导数f″(x)>0,则函数f(x)是区间I上的凹函数.
解由f′(x)=(-x2-2x+1)ex知,曲线f(x)在点x=0处的切线方程为y=x+1.
令f″(x)=(-x2-4x-1)ex=0,
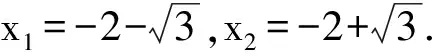
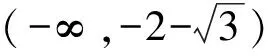
f″(x)<0,此时函数f(x)为凸函数;
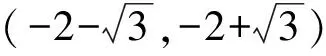
f″(x)>0,此时函数f(x)为凹函数.
故f(x)在x∈[0,+∞)上是凸函数,所以当x∈[0,+∞)时,曲线弧f(x)始终位于其在在点x=0处的切线y=x+1下方(仅在切点处重合).从而当x∈[0,+∞)时,f(x)≤x+1恒成立.从而要使x∈[0,+∞)时,f(x)≤ax+1成立,当且仅当a≥1.
4 适于高中生认知水平的初等解法
上述基于函数凹凸性的高观点解法,揭示了这一类问题的本质,但对高中生而言,因为没有学习函数凹凸性的定义及其判断方法,故仍难以理解.那么,如何基于函数凹凸性的本质找到适合高中生认知水平的初等解法呢?
通过观察图6与图7发现,若函数f(x)在区间[m,n]上为凸(凹)函数.并且曲线f(x)在区间[m,n]左端点处的切线为y=kx+l,则有向线段AB=f(x)-(kx+l)在区间[m,n]上一定是减(增)函数.

图6
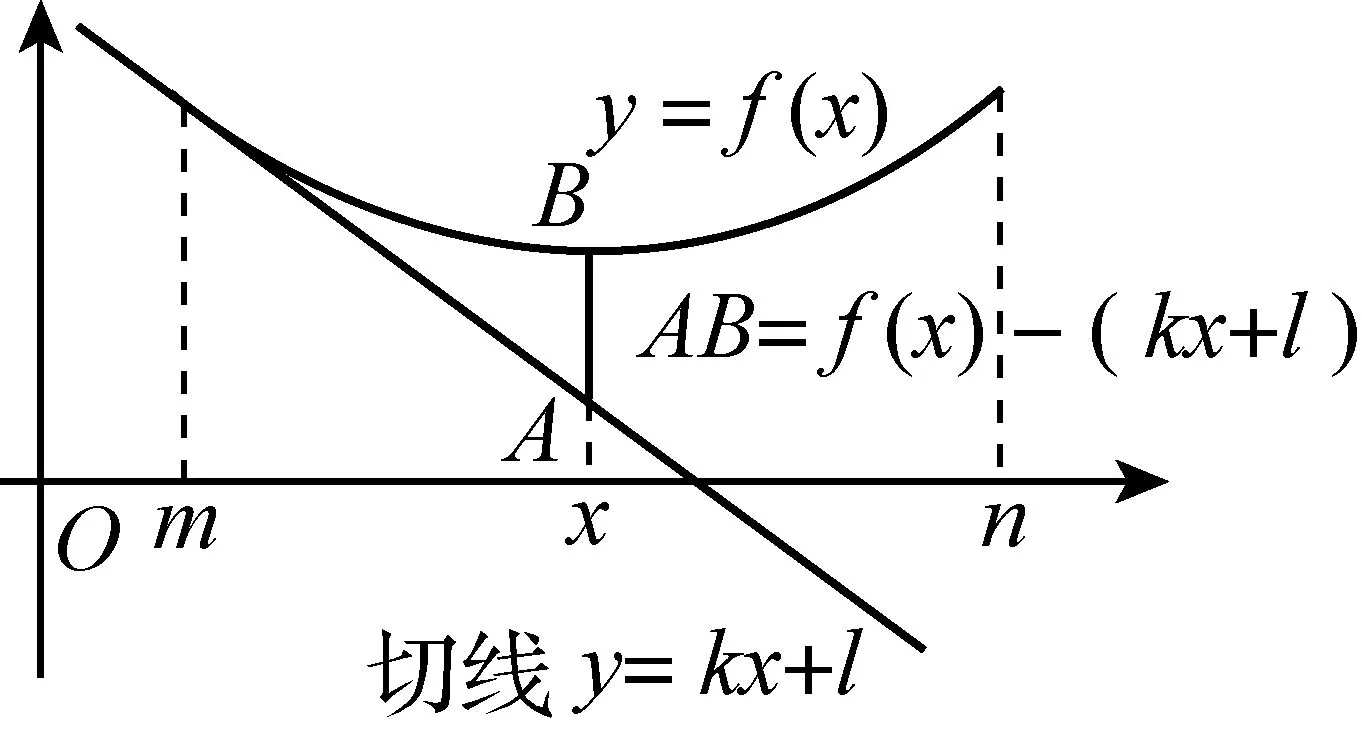
图5
由此得到适于高中生认知水平的初等解法:求出曲线f(x)在区间[m,n]端点处的切线方程y=kx+l,构造函数h(x)=f(x)-(kx+l),进而判断函数h(x)在区间[m,n]上的单调性,从而最终求出参数的取值范围.下面利用上述方法再解例1.
解由f′(x)=(-x2-2x+1)ex知,曲线f(x)在点x=0处的切线方程为y=x+1.
构造函数h(x)=(1-x2)ex-(x+1),
则h′(x)=(-x2-2x+1)ex-1,
h″(x)=(-x2-4x-1)ex.
当x≥0时,显然h″(x)<0,故h′(x)在区间x∈[0,+∞)上是减函数,从而h′(x)≤h′(0).又h′(0)=0,故h′(x)≤0(仅在区间左端点处取等),由此得函数h(x)=(1-x2)ex-(x+1)在区间x∈[0,+∞)上是减函数.
故当x∈[0,+∞)时,h(x)≤h(0)恒成立,即(1-x2)ex≤x+1恒成立.从而要使x∈[0,+∞),f(x)=(1-x2)ex≤ax+1成立,只需x+1≤ax+1,此时a≥1.
下面证明,当a<1时,对x≥0,f(x)≤ax+1不恒成立.
同理,构造函数g(x)=(1-x2)ex-(ax+1),则g′(x)=(-x2-2x+1)ex-a,g″(x)=(-x2-4x-1)ex,显然g″(x)<0,从而g′(x)在区间x∈[0,+∞)上是减函数.
又g′(0)=1-a>0,当x→+∞时,g′(x)→-∞.故必存在充分大的正数m,使得g′(m)<0.由零点存在定理可知,存在唯一的x0∈(0,m),使g′(x0)=0.从而根据g′(x)为减函数可知:当x∈(0,x0)时,g′(x)>g′(x0)=0,即g(x)在区间(0,x0)内是增函数.从而g(x)>g(0),即f(x)>ax+1成立.从而表明,当a<1时,对x≥0,f(x)≤ax+1不恒成立.
综上,可知a的取值范围为[1,+∞).
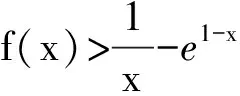
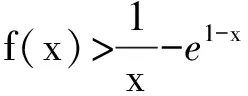
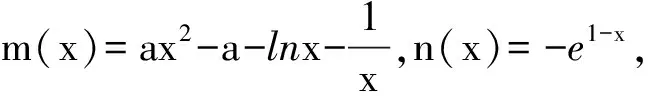
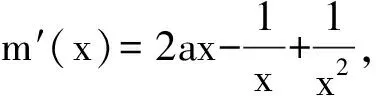
t′(x)=e1-x-2a.
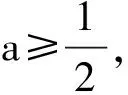
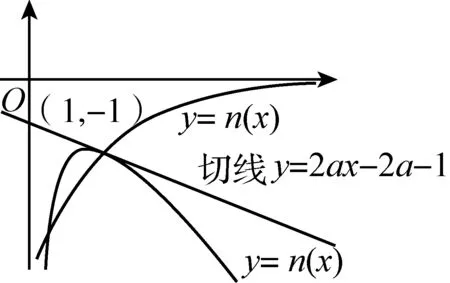
函数s(x)在区间(1,+∞)内是增函数,故s(x)>s(1).又s(1)=0,即s(x)>0,故m(x)>2ax-2a-1对x∈(1,+∞)恒成立(图8).
同理,函数t(x)在区间(1,+∞)内是减函数,故t(x) 图8 图9 (2)∀x∈(1,+∞),若s′(x)<0,t′(x)>0,只需a≤0,此时 函数s(x)在区间(1,+∞)内是减函数,故s(x) 同理,函数t(x)在区间(1,+∞)内是增函数,故t(x)>t(1)=0,即n(x)>2ax-2a-1对x∈(1,+∞)恒成立(图9). 从而,由不等式传递性知m(x) 令t′(x)>0,解得x∈(1,1-ln2a).故函数t(x)在区间(1,1-ln2a)内是增函数,故t(x)>t(1)=0,即n(x)>2ax-2a-1对x∈(1,1-ln2a)恒成立. 本文通过探究形如“当x∈(m,n)时,f(x)≤ax+b恒成立,求a的取值范围”这一类高考试题,揭示出其本质是函数的凹凸性.据此通过构造一类函数,给出了基于高中生认知水平的初等解法,从而表明深入才能浅出,高屋方可建瓴.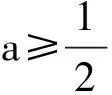

5 结束语
