基于静态台架试验的车体模态贡献量分析

何 理，张立民

（西南交通大学 牵引动力国家重点实验室，成都 610031）

车体作为多自由度的大型振动系统，在线路上运行时，作用于车体的各种激扰力使其产生复杂的振动，且随着车辆运行速度的提高而逐步加剧[1]，严重地影响到列车运行的平稳性与安全性。研究结果表明，速度提高将导致车辆结构发生弹性弯曲振动并引起乘坐舒适性恶化[2]。结构模态作为系统的固有属性，可以较为准确地反映车辆的动态特性[3]。

车辆在静止状态下，通过人为施加激励、测试输入信号与振动响应信号、求解系统振动的频响函数，采用参数识别方法可以识别出系统的特征参数[4]。

一般而言，在既有工作状态下，车体的振动可以用工作变形进行描述，即在特定工况下，对应于特定频率，车体以循环往复的方式表现出各响应自由度之间的相对位移（或相对加速度）的幅值关系[5–7]。应用模态分析技术，研究车体的固有模态以及在不同运行状态下的工作变形，可以真实有效地反应车辆的动态特性。

模态参与因子是各自由度对各阶模态激励有效性的一种度量，模态参与因子较大的模态称为结构的主导模态[8]。在模态参与因子的基础上进一步得到模态贡献量的概念，可以更为直观地描述各阶模态与车体振动能量之间的关系。

1 基于叠加原理的模态贡献量

车体是一个复杂的连续系统，但是在实际工程中为了方便计算，通常将车体简化为多自由度系统[9]。车体运动微分方程可表示为

式中[M]、[C]、[K]分别质量矩阵、阻尼矩阵和刚度矩阵；{f}和{x}分别为系统的激励和响应。

对于系统而言，各阶模态之间相互独立，系统的任意一点响应可以表示为各阶模态振型的线性组合[3]。所以，车体各点响应可表示为[10]

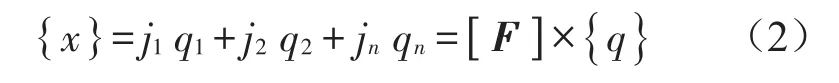
其中[F]为振型矩阵；{q}为各阶振型参与因子组成的向量[11]。

在实际中，车体高阶模态对振动的影响可忽略不计，所以[F]通常不是方阵，则方程{x}=[F]×{q}为超定方程组，可利用最小二乘近似求出{q}。

由式（2）可知，若测得系统的模态振型和响应，便可求出模态参与因子。将模态参与因子归一化，可得

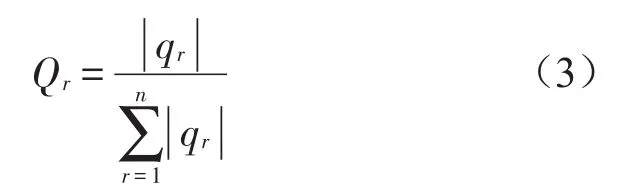
式中Qr为第r阶模态的贡献量，即代表第r阶模态对系统振动能量的贡献比例。

从式（3）可以看出，各阶模态贡献量的和为1，Qr值较大的模态称为主导模态，表明对系统响应的影响最大。

对车体在某一工况下模态贡献量的求解可归纳为：

(1)提取车体各阶模态振型；

(2)提取各测点在某一工况下的响应；

(3)利用式（2）求出各阶模态的振型参与因子；

(4)利用式（3）求出各阶模态贡献量。

2 工程实例分析

2.1 车体模态参数识别

对某地铁车体进行静态台架模态试验，测试其固有频率以及模态振型。由于该车体是钢结构白车体，还未进行总装，所以利用橡胶堆代替空簧约束，将车体坐落在四个橡胶堆上。在车体纵向即垂直于轮轴方向上将车体分为7个截面，分别位于前后端部、一、二位转向架中部、车体中部、1/4定距处和3/4定距处。每个截面布置4个三向加速度传感器，分别位于四个顶点。利用信号发生器产生正弦信号，通过两个激振器对车体输入同步激扰，激励点位于车体前后端部附近的边梁上，激励方向为垂向，两个激励点位于车体同侧。激励采用正弦扫频方式，频率范围为0～50 Hz，扫频速率为0.1 Hz/s，采样频率为1 000 Hz。激励点及测点分布见图1，测试现场见图2所示。

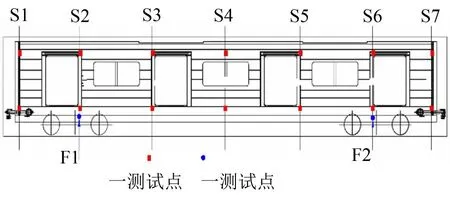
图1 测点和激励点分布

图2 测试现场

基于各个方向的振动互相独立，为了验证该方法的适用性，所以只提取垂向模态参数，针对垂向振动分析其模态贡献问题。对垂向加速度响应数据进行处理后，得到所有测点对F1的综合频响函数，如图3所示。

图3 综合频响函数曲线

进而识别出车体的模态参数。一般来说，总是低阶模态占主导地位[4]，因此只取前12阶模态进行分析。车体模态参数见表1。

2.2 车体模态贡献量计算

计算该地铁车体在不同工况下的模态贡献量。

由于试验采用的是正弦扫频激励，所以用不同的激扰频率来设置工况，如表2所示。

表1 车体模态参数

部分测点的加速度时域信号如图4所示，

截取各个工况下的响应数据后，代入到式（2）中。需要指出的是，由于只提取了前12阶模态振型，所以[F]为28×12矩阵，{q}为12维列向量，而{x}为28维列向量，利用最小二乘近似法求得{q}，然后再根据式（3）计算出各阶模态在不同工况下的贡献量。计算结果如表3、表4所示。

将工况1至工况12各阶模态贡献量绘制成图，如图5所示。

由表2可以看出，在工况1和工况4中，激扰力频率分别为3.1 Hz和12.0 Hz，即为车体的第1阶固有频率和第4阶固有频率，所以车体应该发生以侧滚和1阶菱形为主的振动；由表3可看出，在工况1和工况4中车体侧滚和1阶菱形模态贡献量最大，分别为25.36%和23.51%、27.76%和24.45%，即车体振动能量主要由车体侧滚和1阶菱形贡献，与实际情况吻合。

表2 各工况下激扰力频率

表3 工况1至工况6车体模态贡献量/(%)

表4 工况7至工况12车体模态贡献量/(%)

图4 部分测点加速度时域信号

同时，由图5可以看出，在所有12个工况中，第1、4阶模态的贡献量是所有模态中最多的，其中第1阶模态（侧滚）在每个工况中贡献量最大，基本在25%左右，其次是第4阶模态（1阶菱形），大约在23%左右。所以车体侧滚和1阶菱形在车体振动中占主导地位。

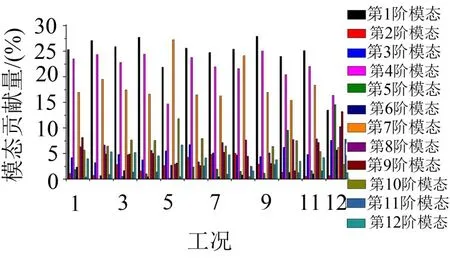
图5 车体模态贡献量

需要指出的是，试验车体受到的是两点、同侧、同相正弦激励，所以车体振动的主要表现形式为侧滚运动和1阶菱形运动，这与上述结论相符合。

3 结语

对某地铁车体进行静态台架试验，提取前12阶模态参数和12个不同激扰频率下车体的响应，分析了车体各阶模态在不同工况下对车体振动的贡献量，现得结果如下：

(1)当激扰力频率分别为3.1 Hz和12.0 Hz时，车体侧滚和1阶菱形模态贡献量最大，分别为25.36%、23.51%和27.76%、24.45%，该计算结果与车体在实际中发生以侧滚和1阶菱形为主的振动相吻合。所以，该方法也可用于计算车辆在线路运行时的模态贡献量，分析出对车体振动影响最大的模态，从而对车体的设计与改进提供可靠依据。

(2)当车体受到两点、同侧、同相正弦激励时，在所有工况中，第1阶模态贡献量都是最大，基本在25%左右，其次是第4阶模态，大约在23%左右，说明车体侧滚和1阶菱形在车体振动中占主导地位。