污染环境中具有Markov切换的随机三种群系统的持久性分析

程铭，谢红梅

（石河子大学理学院数学系，新疆 石河子 832003）

在21世纪，环境问题随着社会的飞速发展而变得日益突出，比如对人类身体产生极大危害的雾霾，因此，对环保部门来说，能够及时采取对策防止环境毒素的超标是相当重要的。许多数学研究工作者也一直在通过建立数学模型的方法量化环境污染对生物种群的作用效果，帮助人们理解环境毒素影响生物种群的作用机制，进而推动了生态毒理动力学的发展。

利用数学模型研究毒素对生物种群生存的影响是20世纪80年代才开辟的一个新领域。Hallam等[1-3]首次提出环境毒素对生物种群生存影响的确定性模型，之后许多学者也相继提出一些确定性模型[4-7]。在现实世界中，种群的生存会不可避免地受到随机干扰的影响。有些干扰是环境中一些较小的扰动，比如湿度、酸碱度、含氧量等细微因素的扰动常用“白噪声”来描述；可是有些干扰会对生物的生长产生较大的影响，比如干旱、地震、洪水等，也有很强的随机性，一旦发生就会引起生物生长的环境迅速由一个状态变为另一个状态，此时可以用“有色噪声”来描述这类扰动。因此，为适应不同的实际情况，讨论污染环境中具有双重噪声扰动的随机模型是非常重要且必要的。

近年来，学者们在随机种群模型方面取得了很好的结果[8-15]，但针对污染环境中具有双重噪声扰动的随机三种群系统的研究还较少，基于此，本文以污染环境中具有Markov切换的随机三种群系统为背景探讨一个极具实际意义的问题，即种群的内禀增长率、生物的体内毒素浓度及系统的双重噪声扰动之间满足何种关系时，能保证种群的数量以大概率位于某一区间内（即使时间充分大）。这一问题的结果将是合理控制环境毒素浓度的理论依据之一。

1 模型

设(Ω,F,{Ft}t∈R+,P)是完备的概率空间，其中{Ft}t∈R+是其滤子并满足通常条件。

定义(B1(t),B2(t),B3(t))是上述完备概率空间上独立的标准布朗运动，则污染环境中种群内禀增长率受白噪声（Bi(t)表示白噪声表示白噪声的强度，i=1,2,3）扰动的随机三种群 Lotka-Volterra模型（SM1）为：

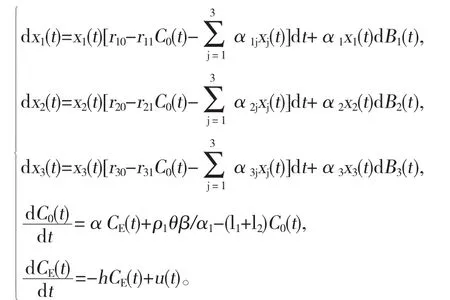
初值条件是C0(0)=CE(0)=0;xi(0)＞0，i=1,2,3。

其中，xi(t),(i=1,2,3)表示时刻t时种群i的数量；C0(t)表示时刻t时生物体内毒素浓度；CE(t)表示t时刻时环境毒素浓度；ri0(ri0＞0)表示毒素不存在时种群i的内禀增长率；ri1(ri1＞0)表示种群i对体内毒物浓度的剂量反应参数；αii(αii＞0)表示种群i的种内作用系数；αii(i≠j)表示种群i与j种群的种间作用系数；参数α1，ρ1(ρ1＜α1)，θ，β，l1和l2都是正常数，α1表示每单位质量的生物体由环境对毒素的吸收率，ρ1表示每单位质量的生物体由食物对毒素的吸收率，θ表示资源中的毒物浓度，β表示单位质量的生物体对食物的摄取率，l1和l2分别表示生物机体对毒物的分解率和排泄率；参数h反应了环境对毒素的清理能力，u(t)表示时刻t时对环境的毒素排放率，且假设u(t)满足 0≤U1≤u(t)≤U2＜∞。

本文在模型（SM1）基础上引入有色噪声。有色噪声可以借助一个在有限状态空间取值的Markov链描述，本文中ξ(t)，t≥0表示完备概率空间(Ω,F,{Ft}t∈R+,P)中一个取值于状态空间S={1,…，k}的右连续Markov链。

本文考虑如下污染环境中具有Markov切换的随机三种群模型（SM2）

且初值条件是C0(0)=CE(0)=0；xi(0)＞0，i=1,2,3，。本文对涉及到的Markov链做以下假设：

假设1Markov链ξ(t)是遍历的，其平稳分布为π=（π1,π2.…πk）且 Markov 链ξ(t)和布朗运动(B1(t),B2(t),B2(t)是独立的。

假设22,3。当种群系统为互惠系统时，

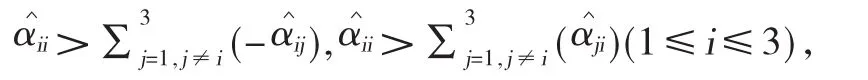
假设3当种群系统为捕食系统时，

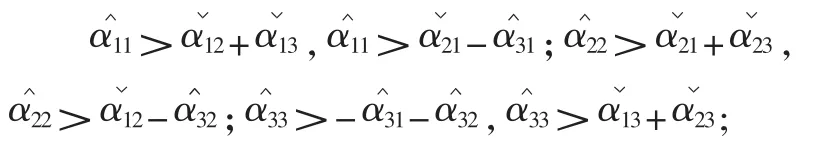
假设 4A(ξ(t))=det(αij(ξ(t)))3×3＞0;(A(ξ(t)))ii＞0;(A(ξ(t)))i＞0，i=1,2,3。其中(A(ξ(t)))ii为A(ξ(t))中元素αii(ξ(t))的代数余子式；(A(ξ(t)))i是将A(ξ(t))的 i列变成而得到的行列式。

假设2和假设3将会在定理1的证明中用到。系统（SM2）虽然是一个五维系统，但由于后2个方程的显式解较易得到，因而实际上只需研究系统的前3个随机微分方程即可，本文称由前3个随机微分方程构成的系统为（SM）。系统（SM）按其生态意义可讨论以下3种情形：

（I）竞争。每一种群的存在对另一种群的增长产生抑制作用。这时

其种间关系可用图1a表示。

（II）互惠。每一种群的存在对另一种群的增长都会起促进作用。这时

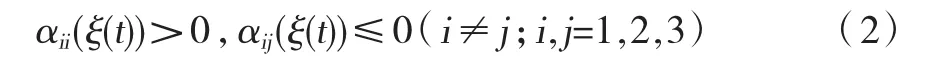
其种间关系可用图1b表示。

（III）捕食。某一种群充当另一种群的食饵，本文探讨的捕食者种群x3(t)除捕食x1(t)与x2(t)外还有其他资源供应（比如虎是食肉性动物，它最喜欢的食物是草食性动物，如鹿、野兔、羚羊和野猪等，而野兔和羚羊之间会相互争夺食物和生存的空间）。这时r30(ξ(t))＞0 且

则x1(t)、x2(t)、x3(t)的种间关系可用图 1c表示。

图1中2条单向箭头表示2个种群之间是竞争关系；一条双向箭头表示两个种群之间是互惠关系；一条单向箭头表示2个种群之间是捕食关系，其中箭头指向捕食者。

图1 种间关系Fig.1 Interspecific relationship

2 引理

在模型（SM2）中，C0(t)和CE(t)皆表示毒素浓度，所以应满足不等式 0≤C0(t)≤1，0≤CE(t)≤1t∈R+，故通过求解模型（SM2）最后2个微分方程可以得到引理 1。

引理 1[14]对模型（SM2），如果 0＜α1+ρ1θβ/α1＜l1+l2，U2≤h，则

0≤C0(t)≤1，0≤CE(t)≤1，

本文假设在模型（SM2）中条件 0＜α1+ρ1θβ/α1＜l1+l2，U2≤h，一直成立。另一方面，在模型（SM）中，xi(t)（i=1,2,3）表示时刻t种群i的数量，故模型（SM）的解过程应该是非负的，这个要求可从引理2体现出来。

引理 2[14-15]系统（SM）对任意的初值(x1(0),x2都存在唯一正解，即(x1(t),x2(t),x3(t))∈

引理3（Chebyshev不等式）[11]令x是Rd-实值随机变量，对于ρ∈(0,+∞)，定义Lp=(Ω;Rd)是Rd-实值随机变量空间，其中E(|x|p)＜+∞，那么

引理4[11]对互惠系统，如果有成立，那么

对于所有的p＞1，都存在一个常数L(p)＞0满足

引理5（随机比较定理）[16]设xi(t)（i=1,2）分别是随机微分方程dxi(t)=fi(xi(t),t)dt+g(xi(t),t)dBt的解，其中f(x,t)∈C([0,∞]×R)，g(x,t)∈C([0,∞]×R)。若还满足

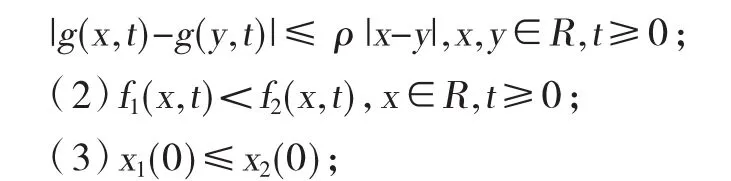
则依概率 1 有x1(t)≤x2(t)，t≥0。

3 种群系统（SM）的随机持久性

随机持久意味着即使时间充分大，种群的数量既不会太大，也不会太小，并且以大概率位于一个区间内。显然，探讨种群系统的随机持久性具有重要的理论和实际意义。本文首先给出系统随机持久的定义。

定义：种群系统（SM）称为是随机持久的，如果对任意给定的ε＞0，存在常数δ＞0，H＞0，使得P*{|x(t)|≥δ}≥1-ε，P*{|x(t)|≤H}≥1-ε成立，其中

定理1在假设1-4成立的条件下，如果有bi＞0，其中

则种群系统（SM）是随机持久的。

证明：将该定理的证明分成以下二步：

（1）首先证明对任意的ε＞0，存在δ＞0，使得P*{|x(t)|≥δ}≥1-ε成立。

令V1(x(t))=1/(x1(t)+x2(t)+x3(t))，则对V1(x(t))使用伊藤公式得

根据定理1的条件，可选取正的常数θ，使得成立，并定义V2(x(t))=(1+V1(x(t)))θ，再对V2(x(t))使用伊藤公式得

取充分小的k满足再定义V3(x(t))=ektV2(x(t))，则根据伊藤公式得到

由下面4个不等式

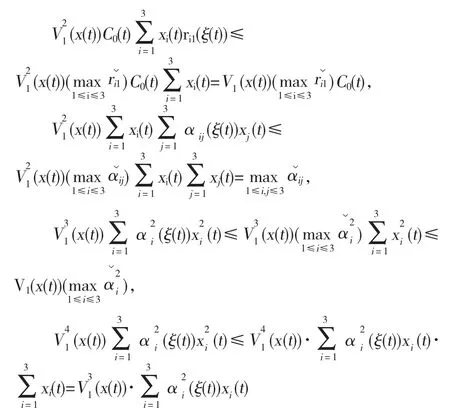
化简可得

故可整理得到

在上式两端积分并取均值得到

再根据V3(x(t))的定义可知

即

对任意的ε＞0，令δ=ε1/θ/M1/θ，由切比雪夫不等式

可得P*{|x(t)|＜δ}≤δθM=ε。这样就证明了P*{|x(t)|≥δ}＞1-ε。

（2）其次证明对ε＞0，存在H＞0，使得P*{|x(t)|≤H}≥1-ε成立。下面针对情形 I、II、III分别讨论种群系统（SM）。

情形I：当种群系统（SM）的种间关系为竞争关系时，对p＞0，令

根据伊藤公式得到

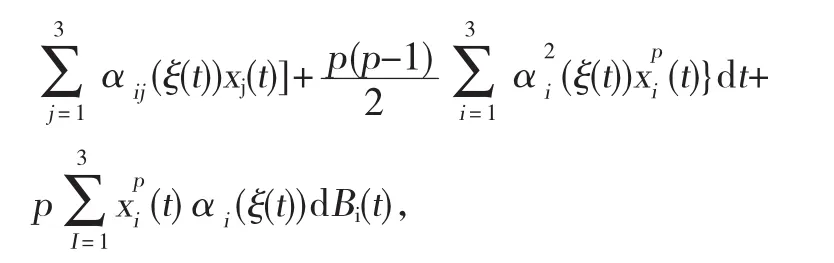
且由情形I得

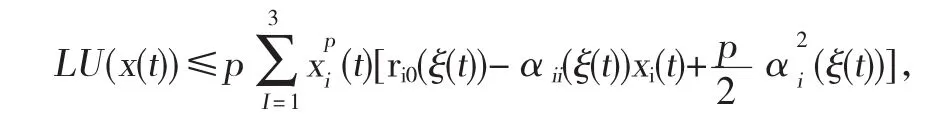
根据此不等式及C Zhu[9]在定理3.1中提到当αii(ξ(t))＞0 且αij(ξ(t))≥0(i,j=1,2… ，n且i≠j）时 有故当时显然有

成立。由切比雪夫不等式得

令H足够大，则证得

（II）当种群系统（SM）的种间关系为互惠关系时，根据假设2及引理4可得

对任意的ε＞0，令H=(3L(2)/ε)1/2，由切比雪夫不等式得

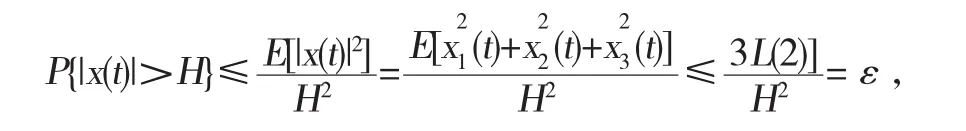
也就是说，P*{|x(t)|＞H}≤ε，即证得

（III）当种群系统（SM）的种间关系为捕食关系时，构造辅助系统（M）如下

其中

显然，辅助系统（M）是一个“互惠系统”。根据随机比较定理知xi(t)≤yi(t)，i=1,2,3，此时的种群系统（SM）满足假设3。那么根据假设3可知，系统（M）的种内、种间作用系数满足假设2，则由定理1证明部分（2）的情形（II）可知，对系统（M）有下式

成立，因此P*{|x(t)|≤H}≥P*{|y(t)|≤H}≥1-ε。

综合以上证明，定理1得证。

4 数值模拟及分析

下面给出数值模拟的例子。

例：设ξ(t)是取值于状态空间S={1,2}的 Markov链，且满足假设 1。令 π=(2/3,1/3)，ri1(ξ(t))=1(i=1,2,3)，则根据种群系统（SM）得到系统（SM3）如下。

下面分别讨论系统（SM3）为竞争、互惠及捕食3种情形的随机持久性。

情形（I）：竞争，令C0(t)=0.51+0.01sint，且种群系统（SM3）中参数在2个状态的取值为：

情形（II）：互惠，令C0(t)=0.62+0.01sint，且种群系统（SM3）参数在2个状态的取值为：

情形（III）：捕食，令C0(t)=0.66+0.01sint，且种群系统（SM3）参数在2个状态的取值为：

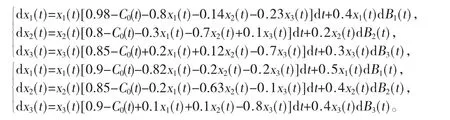
图2 种间关系-竞争

图3 种间关系-互惠

图4 种间关系-捕食

5 讨论与结论

一方面，Mao X[8]、Ouyang M[10]、Liu M[11]研究了随机种群系统的持久性，但并未考虑环境毒素对种群系统的影响；另一方面，靳祯[4]、何继伟[7]、张笑玲[14]研究了污染环境中的种群系统，他们得到的结果多为种群的平均持续生存性与局部灭绝性的充分条件，少有关于种群系统持久性的结果。以此为出发点，针对竞争、互惠、捕食的三种种间关系，本文建立污染环境中具有双重噪声扰动的随机三种群模型，探讨了该种群系统的随机持久性，获得了以下结论：当种群的内禀增长率、生物的体内毒素浓度、及双重噪声扰动之间满足关系