反应扩散方程的分离变量解法
2018-08-30刘怡秀
刘怡秀
(哈尔滨石油学院,黑龙江 哈尔滨 150028)
一、引言
自然界中的很多现象都不可避免地存在着扩散过程,反应扩散方程作为非线性抛物型方程的一类重要模型,被广泛用于描述,解释或者遇见各种自然现象,如来自工程、化学、生物学、医学等众多领域的数学模型均可由反应扩散方程进行描述,因而有着强烈的实际背景。以应用为目的或以其他科学为背景的反应扩散方程的研究,不仅是传统应用数学的一个组成部分,而且也是当代数学研究中的一个重要组成部分,它是数学理论与实际应用之间的重要纽带和桥梁,近年来,对反应扩散方程的研究日益受到重视。分离变量法是求解偏微分方程边值问题的普遍方法之一,其基本思想[1-3]是把多元函数所满足的偏微分方程转化为若干个一元函数的常微分方程,并通过已知的数学知识得到偏微分方程相应的形式解。
二、Dirichlet边界条件定解问题的求解
在本文首先介绍具有Dirichlet边界条件的反应扩散方程形式解。一般地,具有Dirichlet边界条件的反应扩散方程具有如下形式[4]:
(2.1)
其中初始条件:u(x,0)=φ(x),Dirichlet边界条件:u(0,t)=0u(l,t)=0
对式(2.1)利用分离变量法求解其形式解。
令u(x,t)=X(x)T(t)X(x)T(t)≠0,代入方程(2.1)可得:
T′(t)+a2λT(t)=0及X′′(x)+λX(x)=0,并且有X(0)=0,X(l)=0成立。对于方程
X′′(x)+λX(x)=0
(2.2)
在满足X(0)=0,X(l)=0的条件下:当λ≤0时,方程(2.2)只有零解,即X(x)=0。

(2.3)
三、混合边界条件定解问题的求解
对于具有混合边界条件的反应扩散方程,其形式如下:
(3.1)
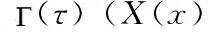
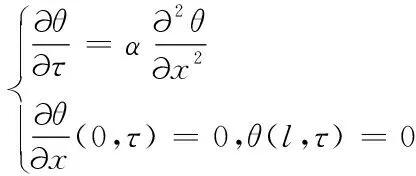
(3.2)
式(3.2)可转化为两个常微分方程:
X′′(x)+β2X(x)=0
(3.3)

(3.4)
微分方程(3.3)的本征值问题为:
X′′(x)+β2X(x)=0,X′(0)=0,X(l)=0
其一般解为X(x)=Acosβx+Bsinβx代入边界条件可得B=0.

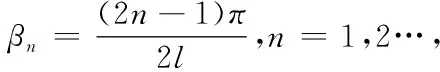
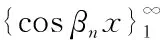
(3.5)
(3.6)
(3.7)
把(3.5)(3.6)(3.7)方程代入(3.1)方程得:
四、结论
分离变量法是求解各种类型的偏微分方程边值问题的普遍方法之一。本文一方面采用分离变量法求解了Dirichlet边界条件的反应扩散方程,另一方面利用该方法求解了具有混合边界条件的反应扩散方程,通过方程的求解为进一步理解分离变量法提供了一定的帮助。
