布谷鸟粒子群混合算法

杨小东，牛俊英，蔡泽凡

（顺德职业技术学院 电子与信息工程学院，广东 佛山 528333）

布谷鸟搜索算法［1-5］（Cuckoo Search Algorithm，CS）是一种启发式算法，灵感来自于布谷鸟寄生哺育幼雏的行为，同时结合鸟类和果蝇的Le'vy fight行为，它由剑桥大学的Xin-She Yang和C.V.Roman工程学院的Suash Deb于2009年共同开发。

粒子群优化算法［6-8］（Particle Swarm Optimiztion，PSO）是模仿鸟群觅食行为的一种群体智能算法，该算法1995年由美国学者 J.Kennedy和R.C.Eberhart提出。PSO算法包括一个速度更新方程和一个位置更新方程，需要调整的参数较少，程序容易实现。

不管是CS还是PSO，得益于它们的简单性和有效性，它们从诞生之日起就引起了广泛关注，并掀起了研究热潮，在诸多领域得到了成功的应用［7-18］。标准的CS全局搜索能力较强，但是其收敛速度较慢；标准PSO算法的前期收敛速度很快，但是全局搜索能力较弱。对于某些复杂问题，这两种算法都存在搜索不到满足精度要求的最优解，其性能需要进一步的改善。结合CS和PSO的优点，引入两种算法的共享机制，形成了布谷鸟粒子群混合算法（Cuckoo Search and Particle Swarm Optimization Mixed Algorithm，CSPSOMA），CSPSOMA大大提升了全局搜索能力和收敛速度。

1 布谷鸟搜索算法

在CS中，存在三个规则［1-3］：规则一：每只布谷鸟1次只生产1颗蛋，并随机选择1个鸟巢存放；规则二：拥有高品质鸟蛋的鸟巢将会被保留至下一代；规则三：可用鸟巢的数量是固定的，而且鸟巢中外来蛋被发现的概率是Pa∈（0，1）。

基于这三个规则，CS包括初始化、搜索、选择和判断四个步骤，各个步骤具体如下：

步骤1：初始化。随机产生N个鸟巢的位置X0=，计算它们的适应度F0，并确定最优的位置。

步骤2：搜索。利用Le'vy fight生成新的位置Xt=，计算新位置的适应度Ft，并确定最优的位置。

Le'vy fight一般采用式（1）所示的随机游走策略。［3］

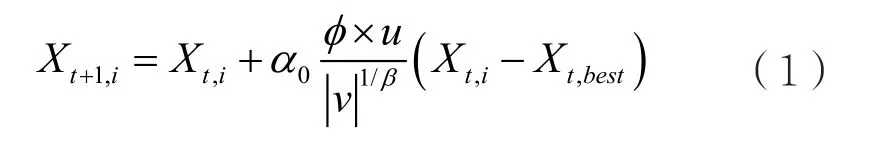
其中，Xt，i表示第 t代第 i个解；Xbest是当前的最优解；α0是步长常数，一般设为α0=0.01；u和v服从标准的正态分布；β为Le'vy fight控制因子，一般β=1.5；Φ用式（2）表示。

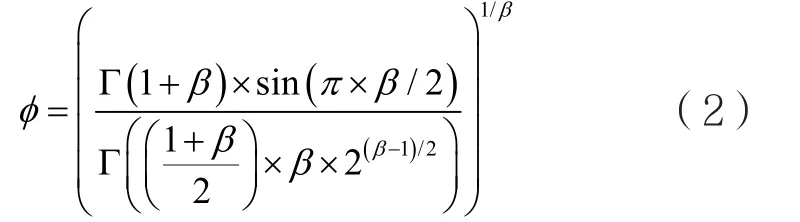
步骤3：选择。按发现概率Pa丢弃差的位置，并采用式（3）产生相同数量的位置代替丢弃的位置。计算所有位置的适应度Ft，并选出最优的位置。

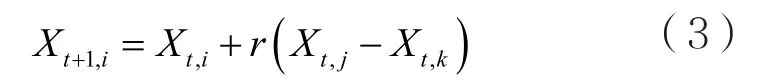
其中，r是缩放因子，在区间（0，1）服从均匀分布，Xt，j和 Xt，k表示第 t代的两个随机解。

步骤4：判断。判断是否达到精度或迭代终止条件，若达到，则终止，否则返回第2步进行迭代更新。

从以上步骤可以看出，CS算法不仅使用了Le'vy fight的搜索方式，还引入了精英保留策略，局部搜索和全局搜索在算法中得到很好的结合。选择步骤增加了位置的多样性，使算法有效的避免陷入局部最优，从而达到全局最优的目的，在迭代次数足够多的情况下，CS能够以1的概率收敛于全局最优解［4］。

2 粒子群优化算法

PSO的基本思想是将每个粒子视为优化问题的一个可行解，粒子的好坏由一个事先设定的适应度函数来确定。每个粒子在可行解空间中运动，并由一个速度变量决定其方向和距离。在每一代进化中，粒子跟踪两个极值：一个是粒子本身迄今为止找到的最优解，另一个是整个群体迄今为止找到的最优解，最终获得问题的全局最优解。

假设粒子群的规模为N，搜索空间为D维，则粒子i在t时刻的状态属性设置如下：

其中1≤d≤D，1≤i≤N。

粒子i在t+1时刻的位置通过式（4）和（5）更新，

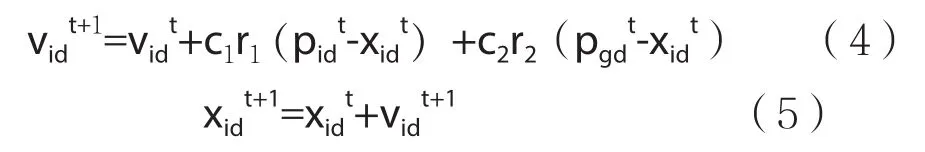
式中，r1、r2为［0，1］区间均匀分布的随机数；c1、c2为学习因子，一般c1=c2=2。

原始PSO算法具有四个步骤：

步骤1：粒子群初始化。设定PSO算法中涉及的各类参数，初始化各个粒子的位置xi和速度vi，计算其适应度Fi；初始化个体自身极值和全局极值。

步骤2：评价粒子群。计算每个粒子的适应度Fi，更新粒子的适应度极值、位置极值Pi，更新全局适应度极值、位置极值Pg。

步骤3：更新粒子群。用式（4）和（5）对每一个粒子的速度和位置进行更新，并对速度的范围进行限制。

步骤4：判断是否满足结束条件。判断是否达到精度或迭代终止条件，若达到，则停止迭代，输出最优解，否则转到步骤2。

3 CS、PSO混合算法CSPSOMA

单一的仿生优化群算法的适应性是有限的，某种算法在解决某个问题时很成功，在处理另外一个问题时则有可能捉襟见肘，而另外一种算法的适应情况可能恰好相反。例如后面在对6个标准测试函数的仿真测试中，CS可以按照规定的精度在限定的迭代次数中搜索到其中5个标准测试函数的最优解，另外1个函数的最优解无法搜索到，而PSO虽然只能以一定的概率搜索到那5个函数的最优解，但是恰好可以概率1搜索到另外1个函数的最优解。另外PSO前期的收敛速度很快，后期则很缓慢，而CS在整个进化周期的收敛速度适中。把PSO和CS进行混合，能够彼此取长补短，提升算法的总体性能。

3.1 CSPSOMA算法流程

在CSPSOMA算法中，CS和PSO有分工也有合作，在单独进化的基础上，每隔一定的代数彼此共享最优个体，从而改善算法的全局搜索能力。CSPSOMA的流程如图1所示，主要包含以下7个步骤：

步骤1：初始化。分别初始化CS和PSO，CS和PSO的族群数和个体的维数相同，目标函数也一致。

步骤2：平行进化。利用CS和PSO分别搜索最优值，两种算法独立的进化，CS和PSO各自保存自己族群的最优个体。

步骤3：选择共享时刻。判断是否到达CS和PSO共享的时刻，这里规定每当算法迭代mg代以后，CS和PSO就进行共享。若到达共享的时刻则进入步骤4，否则跳到步骤5。

步骤4：共享优秀个体。把CS和PSO两者最好的m个个体替换对方最差的m个个体，注意m的值不能超过族群规模的一半，以免发生交换过去的个体又被原封不动的交换回来。随着算法的进化，CS和PSO都可能发生聚集的情况，所以随着算法的进行应该进一步提高族群的多样性，所以m的值宜采取递增的情况，这里采用式（6）进行计算，

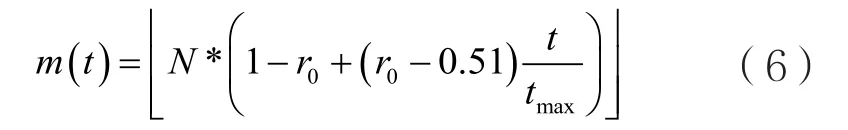
其中，N为族群大小；t为当前迭代数，tmax为最大迭代数；r0为比例控制常数，1≥r0≥0.51；符号表示向下取整数。

另外交换时，需要注意CS和PSO两种算法的不同，在CS中，只需要保存位置和适应度，而在PSO中，除了需要保存位置和适应度以外，还需要保存速度。因此当用CS优秀的个体替换PSO中差的个体时，位置和适应度可以直接替换，但是CS中没有速度信息，我们利用PSO本身最优个体的速度采用混沌模式产生相应的速度序列替换PSO这些较差个体的速度，混沌模式［19-21］采用式（7）的形式。

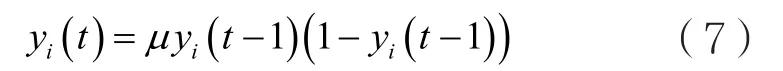
其中，yi（t）是［0，1］中的一个随机数；t是迭代的代数；μ是一个控制参数，一般取4，这时系统将处于一个完全混沌的状态。

步骤5：保存全局最优值。每次进化后，判断CS和PSO两者搜索到的最优值哪一个更优，把其中最优的那一个保存下来。

步骤6：判断算法进程。判断算法是否满足结束条件（达到收敛精度或者最大迭代次数），满足则进入下一步，否则返回步骤2。

步骤7：输出结果。输出最终的最优值结果，算法结束。

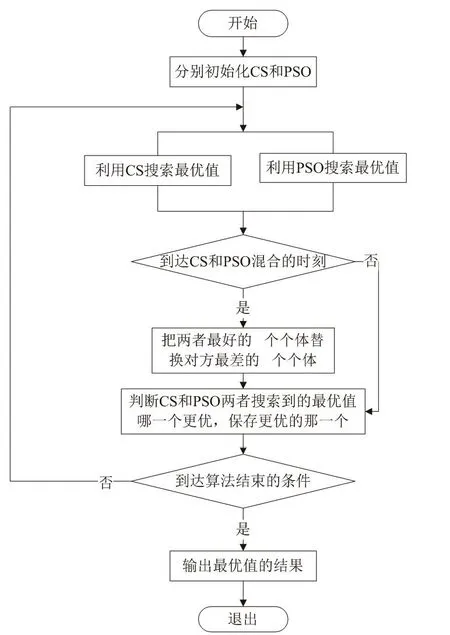
图1 CSPSOMA流程图

3.2 CSPSOMA算法仿真测试

为了验证CSPSOMA算法的有效性而进行仿真测试，仿真测试平台为WIN7+MATLAB R2012b，测试函数采用表1所示的6个标准测试函数，f1～f3为单峰函数，f4～f6为多峰函数。仿真时，族群数n=30，个体维数d=20，各维变量的范围为［-20，20］，函数的收敛精度设为ζ=10-5，最大迭代数设为tmax=2 000，每个仿真单独运行30次。替换代数间隔预设为mg=10，式（6）中的替换比例控制常数预设为r0=0.6，30次测试的结果如表2所示。

由表2可见，函数f3和f5出现了偶尔不能收敛到设定精度的情况，这是始料未及的，可能是由mg和r0这两个参数设置不当引起的，下面以这两个函数作为测试函数，以成功次数和成功时的平均迭代次数作为效果指标，调整mg和r0的值，看看性能是否发生改变。

1）mg的选择。

当r0=0.6固定后，不同的mg对应的特性如表3所示，当mg=100时性能最好，成功率和收敛速度都得到了改善，因此选择mg=100。

2）r0的选择。

当mg=100固定后，不同的r0对应的特性如表4所示，r0=0.6和r0=0.8两者的性能较好，考虑到r0的值越小，两个族群共享的个体数量越多，多样性更好，有利于全局搜索能力，因此选择r0=0.6。

表1 标准测试函数

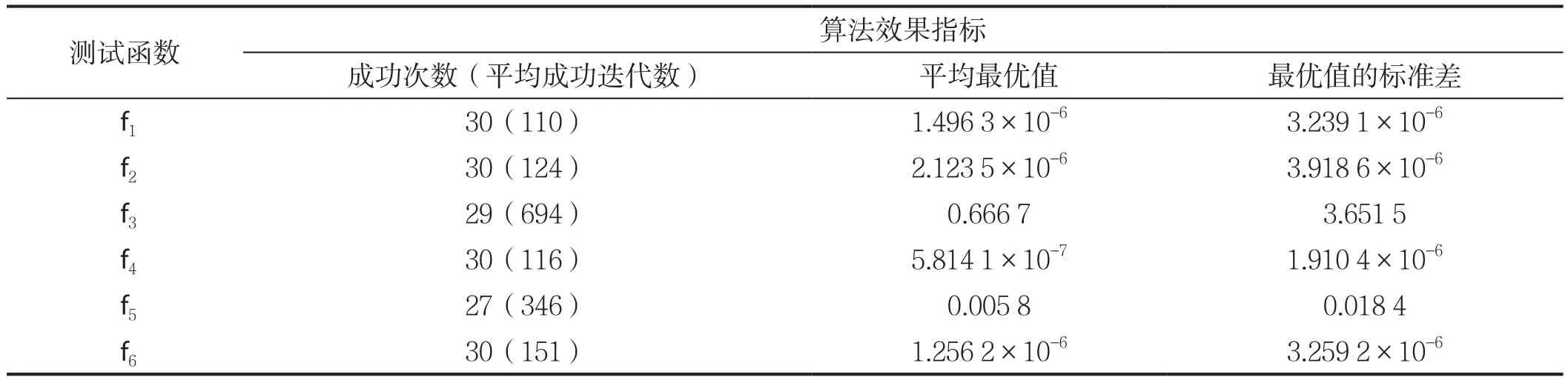
表2 CSPSOMA收敛特性的测试（mg=10，r0=0.6）

表3 mg对收敛特性的影响（r0=0.6）

表4 r0对收敛特性的影响（mg=100）

选定mg=100和r0=0.6后，对另外4个标准测试函数再做一次测试，测试结果如表5所示，对比表5和表2的结果，mg改为100以后，算法在成功率和收敛速度都得到了改善，这种修改是有效的。

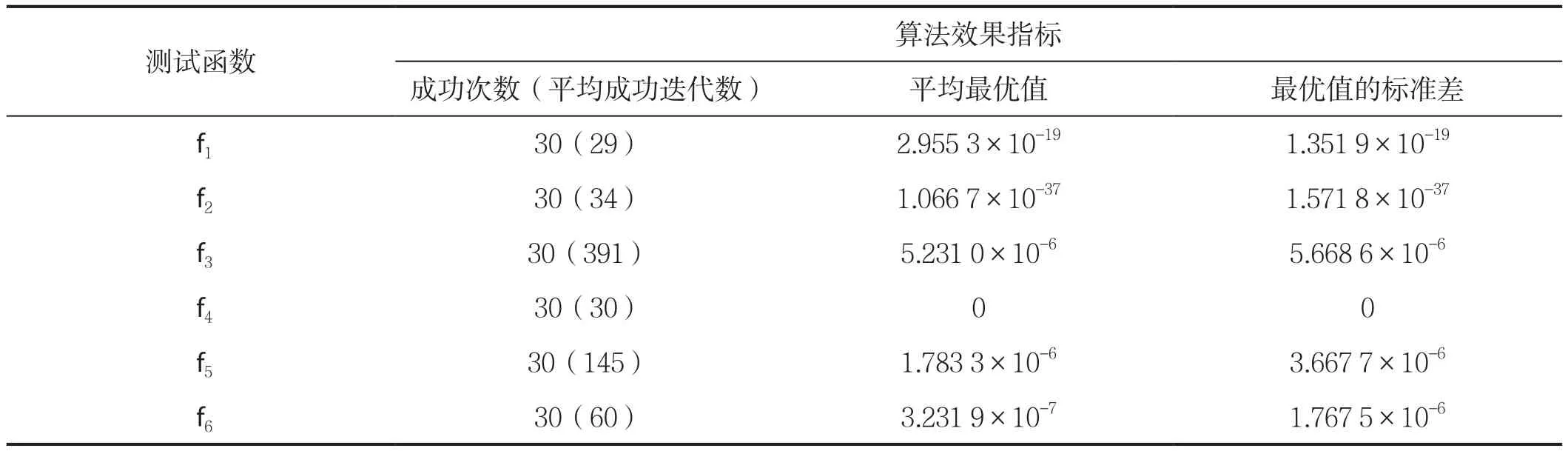
表5 CSPSOMA的收敛特性的测试（mg=10，r0=0.6）

我们再把CSPSOMA、PSO和CS这3种算法的结果放在一起进行比较，结果如表6所示，以成功率和平均成功迭代次数对表6进行汇总，得到表7。

由表7可见，在成功次数（代表了成功率）方面的排序为CSPSOMA＞CS＞PSO，而在平均成功迭代次数（代表了收敛速度）方面的排序为PSO＞CSPSOMA＞CS，虽然PSO的收敛速度最快，但是它牺牲了成功率，而对于优化算法来说，成功率是最重要的，因此从总体性能上来看，这3种算法的排序为 CSPSOMA＞CS＞PSO。

表7是对成功率和成功时的收敛速度来考察的，现在我们再来看看它们的平均性能，以标准测试函数 f3和f6为例，利用PSO、CS和CSPSOMA这4种算法迭代2 000次，重复30次以后取平均值，对应的平均最好适应度曲线如图2和图3所示。

从图2可见，PSO和CSPSOMA这2种算法在开始的几十次迭代中，收敛速度是一样的，但是PSO出现了不能收敛的情况，取平均以后导致整体的性能很差。CS在约400次迭代以前收敛速度最慢，大概400次迭代以后下降速度明显好于PSO，而CSPSOMA则吸取了CS和PSO两者的优点，基本上每个时刻都取到了CS和PSO两者中性能最好的那一个。

图3和图2的情况基本相同。

综合表7、图2和图3的信息，我们可以得到这样的结论：从总体性能上来看，这3种算法的排序为 CSPSOMA＞CS＞PSO。

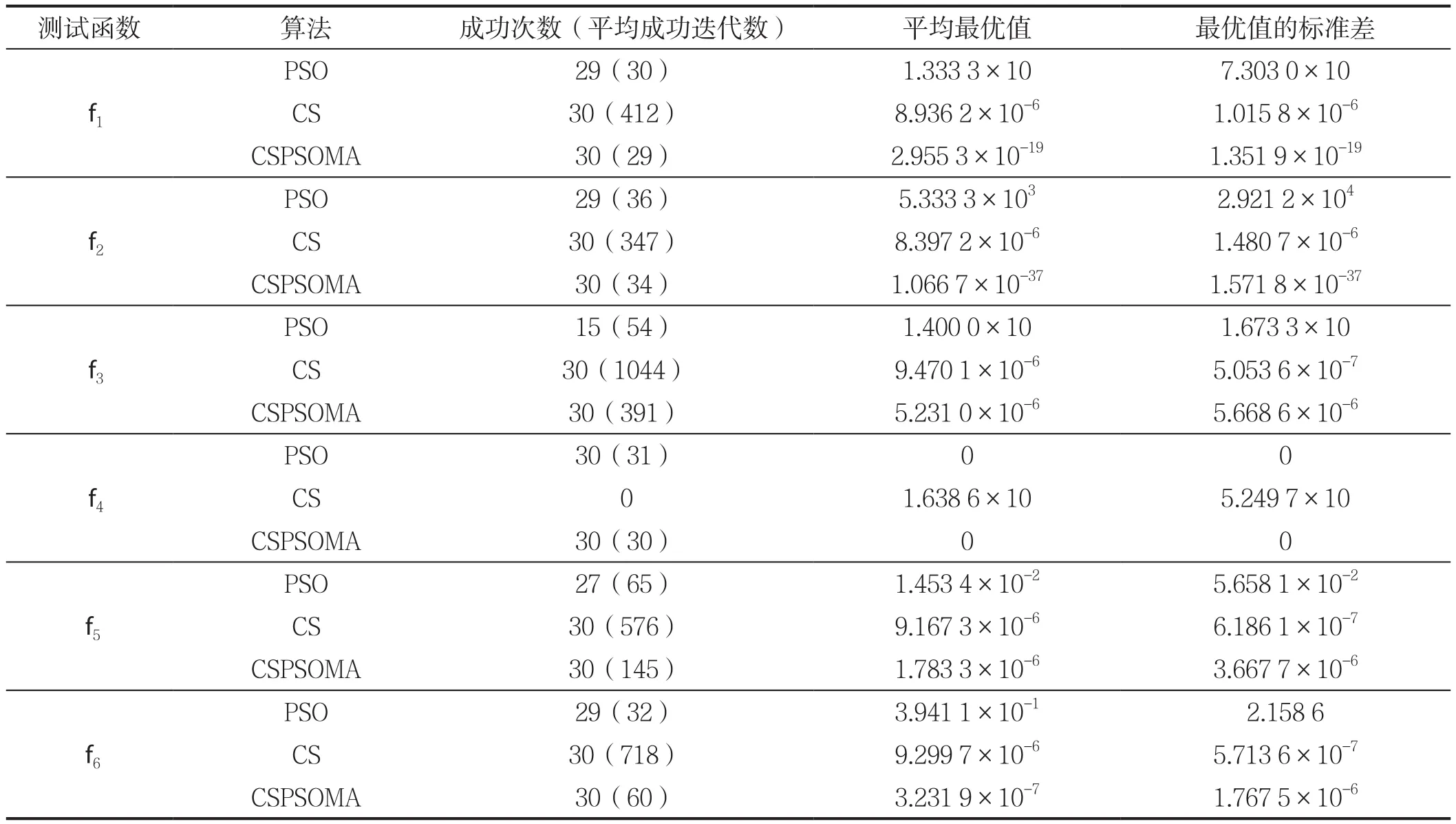
表6 CSPSOMA、CSPSOMA、PSO和CS的仿真对比情况

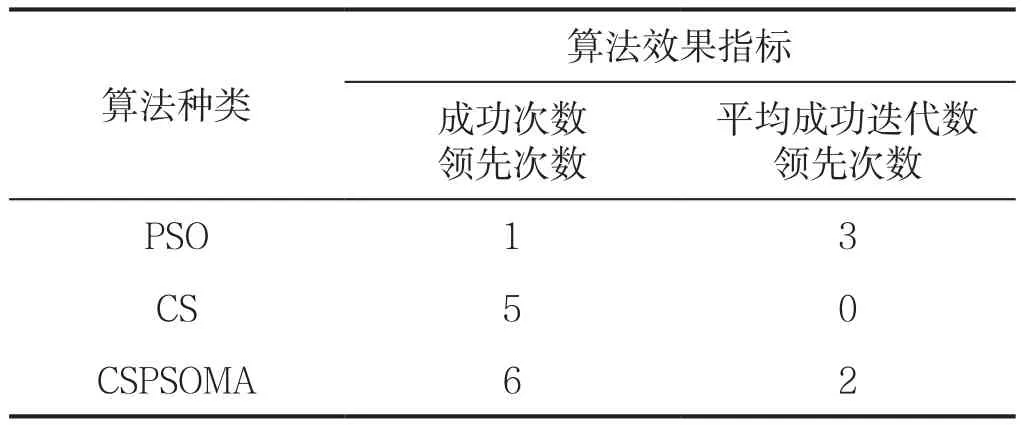
表7 函数f1～ f6的仿真结果汇总表

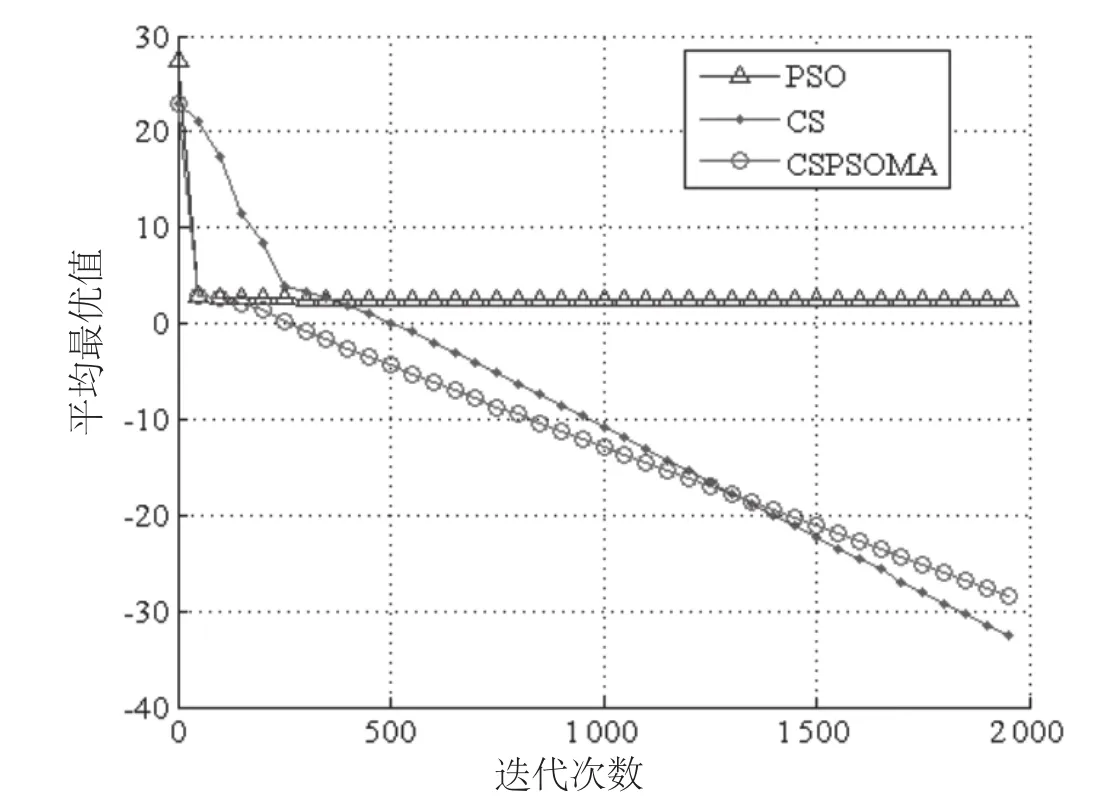
图2 函数f3的平均最优适应度曲线

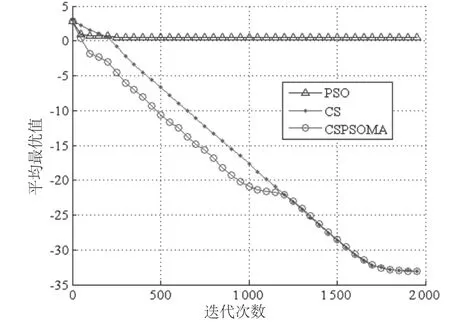
图3 函数f6的平均最优适应度曲线

4 结论

单一的仿生优化群算法无法适应所有的优化问题，不同的优化算法具有各自适合的场合，将两种或以上的仿生算法进行混合，可以做到扬长避短，提升算法的适应性。CSPSOMA结合了CS、PSO两者的优点，六种标准测试函数仿真情况表明，CSPSOMA的性能明显好于PSO和CS，不管是处理简单的单峰函数，还是复杂的多峰函数，CSAPSO的全局搜索能力和收敛速度都更加优越，表现了良好的鲁棒性。