水波与双重不同竖直刚性薄板相互作用的理论研究*

2018-08-29汪利先金春伟

武汉理工大学学报（交通科学与工程版） 2018年4期

汪利先金春伟

(武汉理工大学交通学院武汉 430063)

0 引言

防波堤是海岸与海洋工程中的一种重要的水工建筑物结构，其主要作用是防御波浪入侵，为港口码头等形成掩蔽水域.基于波浪能量集中在水体表层的特点，许多专家学者提出了一种新型结构防波堤，即自由面防波堤.这种防波堤主要包括透空式防波堤和浮式防波堤，其利用上部的挡浪结构衰减外海传来的大部分波浪，而在下部允许水体通过，这样既可以达到较好的掩护效果，又可以保证所掩护区域具有良好的水质条件.同时，其还具有成本低、适用水深范围广，以及对水底地质要求低等优点，因此，关于自由面防波堤的研究工作是海岸工程和海洋工程界的热点课题之一[1-2].

由置于自由液面附近的双重竖直刚性薄板所组成浮式防波堤是一种典型自由面防波堤结构.基于线性波理论，Mciver等[3-6]对波浪与双重相同竖直刚性薄板在无限深水或有限均匀深水中的相互作用的展开了广泛的研究，并计算了这种结构的反射与透射系数等水动力特性.但是，目前国内外对波浪与双重不同竖直刚性薄板相互作用的研究相对较少， Evans等[7]研究由一个穿透水面、另一个浸没水下并向下无限延伸的两个竖直刚性薄板组成的结构与正向波的相互作用问题，并考虑了斜向入射波和有限深水的情况.另外，他们使用的是变分方法结合多项伽辽金逼近法，得到了非常准确的反射系数和透射系数.文献[3]应用匹配特征值函数法定性研究了有限深水中正向波与双重不同穿透水面刚性竖直薄板的相互作用，但是没有考虑薄板吃水、两板间距等因素对反射系数的影响，也没有计算作用在薄板上的波浪力.Roy等[8-9]采用积分方程和单项伽辽金逼近法,研究了三组不同的双重刚性薄板与斜向波在无限深水的相互作用，其中一组穿透水面，一组则是完全浸没并向下有限延伸，还有一组完全浸没并向下无限延伸.

本文利用匹配特征函数展开法求解边值问题，并应用最小二乘法处理混合边界条件，得到了穿透水面的双重不同竖直刚性薄板的波浪绕射问题的解析解，系统地分析了两板吃水比、后板吃水、两板间距等因素对反射系数和水平波浪力的影响规律.研究的结果可为新型防波堤的物理模型试验和工程实践提供参考.

1 边值问题

图1为当前研究问题的理想化示意图.考虑到竖直刚性薄板的厚度远小于入射波长，可将其忽略.在有限均匀水深h的计算水域中，规则波浪从左至右正向入射.直角坐标系的原点O位于左侧竖直薄板与静水面的交点处，X轴水平向右，Z轴垂直向上.前、后两竖直薄板的吃水深度分别为d1，d2，两板之间的间距为b.根据竖直薄板的水平位置，将整个计算流域划分为三个区域：区域1(-∞≤x≤0，-h≤z≤0)，区域2(0≤x≤b，-h≤z≤0)；区域3(b≤x≤+∞，-h≤z≤0).

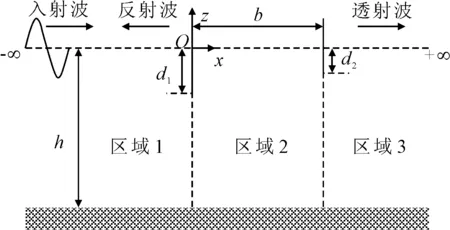
图1 正向波与双重不同竖直刚性薄板的相互作用示意图

1.1 控制方程

基于势流理论，当入射波为圆频率(的线性规则波时，计算区域j中流体运动的速度可以用速度势Φj表示为

Vj(x,z,t)=Φ(x,z,t)=

(1)

式中：Re为对变量取实部；φj为与时间t无关的空间速度势.

将流体视为无粘不可压缩理想流体并假设流体运动无旋，则空间速度势φj应满足拉普拉斯方程

2φj(x,z)=0,j=1,2,3

(2)

1.2 边界条件

空间速度势除了需要满足式(2)的控制方程外，还需要满足以下边界条件，包括：

线性化的自由水面条件：

∂φj/∂z=ω2/gφj,j=1,2,3

(3)

海底边界无穿透条件：

∂φj/∂z=0,j=1,2,3

(4)

无穷远处辐射边界条件：

∂φR/∂x=-ik0φR,x→-∞

(5)

∂φT/∂x=ik0φT,x→+∞

(6)

前、后薄板表面无穿透条件：

∂φj/∂x=0,-d1≤z≤0,x=0,j=1,2

(7)

∂φj/∂x=0,-d2≤z≤0,x=b,j=2,3

(8)

区域1，2分界面上速度及压力连续边界条件：

∂φ1(x=0-,z)/∂x=

∂φ2(x=0+,z)/∂x,-h≤z≤-d1

(9)

φ1(x=0-,z)=

φ2(x=0+,z),-h≤z≤-d1

(10)

区域2、3分界面上速度及压力连续边界条件：

∂φ2(x=b-,z)/∂x=

∂φ3(x=b+,z)/∂x,

-h≤z≤-d2

(11)

φ2(x=b-,z)=φ3(x=b+,z),

-h≤z≤-d2

(12)

式(3)～(12)中：g为重力加速度；k0为入射波波数；φR、φT分别为反射波、入射波空间速度势.

2 解析方法

2.1 特征值函数展开法

三个计算区域中的空间速度势φj可以展开为适当形式特征值函数的叠加.采用分离变量法，满足式(2)及式(3)～(6)的速度势可以写为

φ2=

(13)

φ2(x,z)=

(14)

φ3(x,z)=

(15)

式中：A为入射波波幅；Rn，Tn，An，Bn(n=0,1,2,3,…)为未知的展开系数；kn为波数；Zn为沿水深变化的垂向特征函数：

Z0(k0z)=

(16)

波数kn满足水波运动的线性色散关系：

ω2=gk0tanh (k0h)=

-gkntan(knh)，n=1,2,…

(17)

令α0=-ik0，αn=kn，n=1,2,…，则式(13～15)可以改写为

φ1(x,z)=

(18)

φ2(x,z)=

(19)

(20)

为了求解上式中的未知系数Rn，Tn，An，Bn(n=0,1,2,…)，将式(18)～式(19)代入区域1，2分界处x=0处法向速度连续的边界条件，即式(7)和(9)，可得

R0=1-A0+B0e-α0b,Rn=

-An+Bne-αnb,n=1,2,…

(21)

类似地，将式(19)～式(20)代入区域2，3分界处x=b法向速度连续的边界条件，即式(8)和(11)，可得

Tn=Ane-αnb-Bn,n=0,1,2,…

(22)

由式(21)～(22)可知，只需求解出An，Bn(n=1,2,…)，就可以得到上节中边值问题的完整解析解.

将式(18)、(19)和(21)代入到区域1、2分界处x=0压力连续的边界条件，即式(10)，可得

(23)

将式(18)和(21)代入到前薄板x=0处的无穿透边界条件，即式(7)，可得

0,-d1≤z≤0

(24)

将式(19)、(20)和(22)代入到区域2、3分界处x=b压力连续的边界条件，即式(12)，可得

(25)

将式(19)代入到后薄板x=b处的无穿透边界条件，即式(8)，可得

0,-d2≤z≤0

(26)

2.2 最小二乘法

式(23)～(24)为关于An，Bn(n=0,1,2,…)在区域1、2分界处x=0的对偶级数方程组，分别给出了部分边界上的狄利克雷条件和诺依曼条件.同样地，式(25)～(26)为区域2、3分界处x=b的对偶级数方程组.为了确定这两组未知展开系数，需将分界处上的两个部分边界条件转化为的一个混合边界条件，给出沿水深方向的速度势或速度.

在分界处x=0，令

(27)

为了在沿水深方向-h≤z≤0满足S(z)=0，根据最小二乘法应满足

最小值

(28)

因此可得

(29)

式中：S*(z)为S(z)的共轭.

类似地，在分界处x=b，令

(30)

根据最小二乘法应满足

(31)

将式(29)和(31)中的m，n均截断到N项，联立求解，可以确定展开系数An，Bn(n=0,1,2,3,…,N-1,N)，也就获得了计算区域流场内任意位置的速度势.

2.3 反射系数、透射系数和水平波浪力

反射系数、透射系数分别定义为反射波高、透射波高与入射波高的比值.由图1可知，区域1中包含入射波和反射波成分，其空间速度势表达式(13)中的第一项对应于入射波，第二项对应于反射波，第三项对应于非传播模态波,因此，反射系数可为

CR=|R0

(32)

区域3中仅包含透射波成分，其空间速度势表达式(15)中的第一项对应于传播透射波，第二项对应于非传播模态波，则透射系数为

CT=|T0|

(33)

计算流域内的动水压强可以利用非稳态伯努利方程求得

P(x,z)=iρωφ(x,z)

(34)

将动水压强沿薄板表面积分，可以分别得到作用在单位宽度前、后薄板上的水平波浪力Ff、Fr：

(35)

(36)

3 结果与讨论

首先利用其计算了正向波与双重相同竖直刚性薄板相互作用问题.计算相关的参数选取为：前后薄板的吃水深度相同(d1/d2=1)，无因次后板吃水深度(d2/h)为0.2，无因次两板间距(b/h)为0.6.为了保证计算结果的收敛精度，必须合理的选择式(29)和(31)中的截断项数N.计算试验表明，当N=400时，可以保证本文的计算结果精度为10-2，足以满足工程计算所需，因此，在下文中，无特殊说明时均采用这一截断项数.正向波绕射双重相同薄板的反射系数随入射波频率变化的计算结果见图2.由图2可知，本文的计算结果与文献[5]中的结果吻合较好，证明了本文解析计算方法的正确性.另外，还同时验证了不同入射波频率情况下的波浪能量守恒关系，即反射系数与透射系数应满足CR2+CT2=1，进一步证明了本文解析计算方法的正确性.

d1/d2=1;d2/h=0.2;b/h=0.6.图2 正向波绕射双重相同薄板的反射系数随入射波频率变化的计算结果图

3.1 两板吃水比对水动力的影响

图3为五种不同两板吃水比即d1/d2=0.25，0.5，1，1.5，2所对应的反射系数随入射波频率变化的曲线.计算时固定后板吃水为d2/h=0.3，两板间距为b/h=0.6.由图3可知，反射系数随着入射波频率的增加单调递增至1，即在高频区发生全反射.当两板的吃水相同时(d1/d2=1)，反射系数随入射波频率先减小后增大.本文的解析计算结果表明：在频率为ω2/gh=1.67附近，反射系数存在一个接近0的极小值(0.45%)，而双重不同薄板对应的反射系数曲线则不存在类似的零反射系数的极值点.这表明双重不同薄板与双重相同薄板存在显著的水动力差异.由文献[3]可知，当两板完全相同时，必定在某一频率存在零反射；当两板不同时，对应的反射曲线显著不同，不能满足在同一频率处的反射系数相等的条件，则零反射现象不存在.考虑到本文的计算精度，本文的计算结果与文献[3]中的理论分析相吻合.另外，由图3可知，当前板吃水大于后板吃水时(d1/d2>1)，随着两板吃水差异的增大，低频区的反射系数也随之增大.

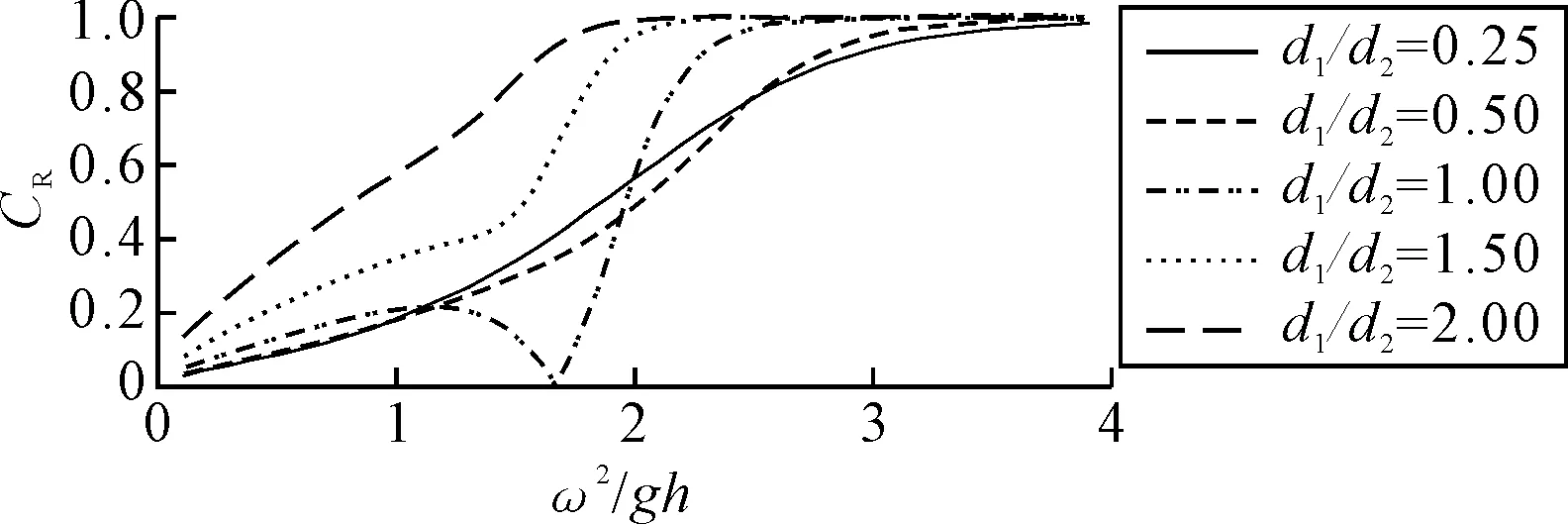
d2/h=0.3;b/h=0.6.图3 不同两板吃水比情况下反射系数随入射波频率的变化图

图4为不同两板吃水比情况下作用在前、后板上的无因次水平波浪力|Ff|/(gAd1、|Fr|/(gAd1随入射波频率的变化曲线.由图4a)可知，前板所受的水平波浪力随入射波频率先增加后减小，存在一个峰值.当两板吃水比不断增大时，水平波浪力峰值对应的频率向低频区移动.当吃水比为d1/d2=0.25时，水平波浪力峰值为0.87，对应的峰值频率为ω2/gh=3.4；当吃水比增大至2时，水平波浪力峰值为1.7，对应的峰值频率减小为1.6.另外，可以发现当双重薄板相同时(d1/d2=1)，作用在前板上的水平波浪力峰值最大，约为双重不同薄板(吃水比d1/d2=2)的1.31倍.因此，布置双重不同薄板能显著减小作用在前板上的波浪载荷.由图4b)可知，作用在后板上的水平波浪力曲线与前板相似，但其峰值对应的频率随两板吃水比的增大逐渐向高频区逐渐移动，这与前板的情况正好相反.当吃水比为0.5时，对应的水平波浪力峰值最大，达到1.56，约为双重相同薄板的1.06倍.当吃水比为2时，对应的水平波浪力峰值约为双重相同薄板的44%.

d2/h=0.3;b/h=0.6.图4 不同两板吃水比情况下水平波浪力随入射波频率的变化图

3.2 后板吃水对水动力的影响

图5为不同后板吃水(d2/h)情况下反射系数随入射波频率变化的曲线.计算时固定两板吃水比为d1/d2=0.5，两板间距为b/h=0.6，后板吃水d2/h从0.1变化到0.5.由图5可知，当薄板吃水较小时(d2/h<0.3)，，反射系数随入射波频率单调递增.当薄板吃水较大时(d2/h>0.3)，反射系数随入射波频率先单调递增，后至临界频率处不再发生明显变化，此时反射系数达到其理论最大值1.后板吃水为d2/h=0.5对应的临界频率为ω2/gh=2.3.另外，当薄板的吃水增加时，反射系数在低频区随之增大.如在入射波频率为ω2/gh=1时，后板吃水为d2/h=0.5的反射系数约为d2/h=0.1的反射系数的21倍.

d2/h=0.3;b/h=0.6.图5 不同后板吃水情况下反射系数随入射波频率的变化

图6为五种不同后板吃水所对应的前、后两板的水平波浪力随入射波频率的变化曲线.与图4相似，在所考虑的频率范围内，除d2/h=0.1外，前、后板的水平波浪力均存在一个峰值.当前、后两板的吃水逐渐增大时，该峰值逐渐增大，并且对应于该峰值的入射波频率朝低频区移动.显然，随着薄板吃水的增大，所受的流体动压强的影响范围显著增大，最终导致水平波浪力的增加.

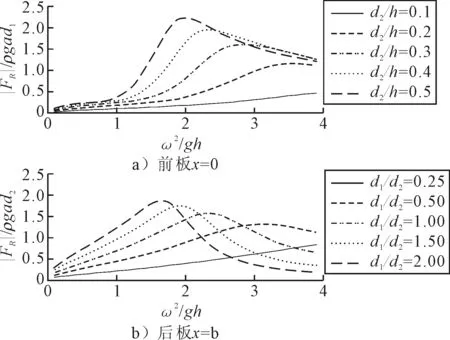
d1/d2=0.5;b/h=0.6.图6 不同后板吃水情况下水平波浪力随入射波频率的变化

3.3 两板间距对水动力的影响

图7为不同板间距(b/h)所对应的反射系数曲线.计算时固定两板吃水比为d1/d2=0.5，后板吃水为d2/h=0.3.可以看出，随着入射波频率的增大，反射系数的总体趋势是逐渐增大.当两板间距大于b/h=0.6时，反射系数波动上升，存在两个极值点.当b/h=1.2时，在入射波频率为ω2/gh=2.8和3.2附近，反射系数分别存在极大值和极小值.当b/h=2.4时，在ω2/gh=2.6和2.9附近分别存在极大值和极小值.

d1/d2=0.5;d2/h=0.3.图7 不同两板间距情况下反射系数随入射波频率的变化

图8为不同两板间距对前、后板水平波浪力的影响关系曲线.两板间距对作用在前后板上的波浪力影响比较复杂.由图8a)可知，当两板间距为b/h=0.15时，前板所受水平波浪力随入射波频率单调递增.当b/h=0.3和0.6时，前板波浪力在所考虑的频率范围内为单峰曲线.当b/h>0.6时，水平波浪力随入射波频率的变化曲线存在两个极大值.由图8b)可知，当b/h<2.4时，作用在后板上的水平波浪力曲线均为单峰曲线.当两板间距增大为b/h=2.4时，水平波浪力ω2/gh=2和3附近均存在极大值.