基于STAR-CCM+的水动力翼 对双体船阻力影响研究*

姚国全 刘 颖 赵应江 邱 鹏

(武汉理工大学交通学院1) 武汉 430063) (国家知识产权局专利局专利审查协作湖北中心2) 武汉 430205)

0 引 言

我国颁布的《“十二五”节能减排综合性工作方案》对于船舶节能减排提供了指导性方向，IMO、船级社、交通运输部对于船舶EEDI和EEOI标准指标的强制执行，为船舶节能减排提供了具体技术指标[1-3].在严格控制排放量的同时，也要开发更加高效、环保的高性能船舶.高速双体船在阻力、操纵、稳性以及使用性能方面具有明显的优势,而近年来复合型双体船受到了越来越多的关注，它不仅结合了多种优良船舶的优点，也为新型船舶的设计提供了更多思路，将水翼应用于双体船便是一种创新设计，国内外对水翼双体船的研究已经取得了一定成果，并将部分成果应用于实船，获得了不错的成绩.

Souto等[4]通过拖曳水池模型试验对片体间距调节来研究间距大小对双体船阻力性能的影响.Broglia等[5]则结合数值仿真和试验的方法进行了双体船兴波干扰影响的研究，其研究结果表明片体间距越短，干扰效应越强，通过数值仿真进行深入分析，得到压力场和速度场更加细致的数据，数值仿真与模型试验的误差小与2.2%，仿真结果有很高的可信度.Kandasamy等[6]研究了一种低兴波高速水翼双体船的优化，其中对水翼的安装位置，角度以及片体间距对远域兴波的影响进行了研究.Bruzzone等[7]通过在艏部片体之间安装中央水动力球体研究其对双体船耐波性的影响.国内关于双体船阻力性能以及片体间的兴波干扰也有一定的研究，李绍波等[8-9]对双体船兴波阻力数值计算和兴波干扰进行了研究.李国安等[10]对近水面水翼影响的船舶兴波进行了时域计算研究.汪礼[11]对近水面水翼对双体船水动力性能进行了初步研究.陈庆任等[12-13]对近自由面三维水翼的水动力进行了数值模拟和试验研究.

本文将采用STAR-CCM+软件进行高速双体船的数值模拟，通过分析数值模拟和模型试验结果，验证STAR-CCM+应用于双体船水动力性能模拟的可行性，并在此基础上尝试探索水动力翼在双体船减阻方面的应用，最后进行模型试验进行验证，得到水动力翼的安装位置和角度对双体船阻力的影响.

1 基于STAR-CCM+的双体船数值仿真

1.1 控制方程及湍流模型

假定流体为不可压缩流体，其连续性方程及动量守恒方程表达式为

连续方程：

(1)

式中：ρ为密度；t为时间；μi为速度矢量u在xi方向的分量.

动量方程(Navier-Stokes 方程)：

(2)

式中：μj为速度矢量u在j方向的速度分量；p为流体微元体上的压力；Si为质量力；μ为黏度.

此次模拟使用VOF两相流模型，对同一连续体内的两种流体(空气和水)进行建模，并采用基于平均雷诺数方程(Reynolds-Averaged Navier-Stokes)求解瞬态的粘性绕流场的数值方法，计算时采用k-ε湍流模型，利用有限体积法对计算区域进行离散，使用隐式不定常进行求解，时间步长为0.02 s，每个时间步长迭代八次[14-15].

1.2 计算模型和仿真过程

本文的计算模型采用一高速双体船模型，缩尺比为8.75，模型主尺度见表1.为建立高精度的船体三维模型，采用CATIA进行建模，建模过程中运用宏命令快速导入型线，并对球鼻艏添加了多条辅助型线，在保证曲面光滑过度的情况下，也尽量提高了模型精度，完成的三维模型图见图1，模型表面光顺，精度较高，符合计算需求.

表1 高速双体船主尺度

图1 高速双体船模型

计算域为36 m×18 m×27 m, 网格划分在STAR-CCM+中进行，划分技巧主要是对流动复杂区域如自由液面处，艏艉以及片体间区域进行适当网格加密，并保证网格间过度均匀.本次仿真采用切割体网格进行网格划分，使用VOF两相流进行仿真，采用6DFHI模拟模型的纵摇和升沉运动，并监测摩擦阻力，兴波阻力，总阻力等多个物理量，对自由液面和船体中部兴波也进行监测.边界条件设置见图2.

图2 边界条件设置

经过多次数值仿真，发现网格密度对结果存在较大影响，网格数较过大不仅会占用过多的计算资源，增加计算成本，还会使计算周期加长，而网格密度过小会使计算结果精度较差，划分合适数量的网格对整个仿真十分重要.本文以设计航速V=2.695 7 m/s为例，对五种不同网格密度进行计算，找到最优的网格划分方式.具体网格和计算的阻力值见表2，由表2可知，在边界层网格为8层，网格数为3×106左右时计算结果趋于稳定.

表2 不同网格数量下的阻力性能比较

1.3 数值仿真与模型试验结果分析

为验证仿真结果的准确性，分别对实船速度V=6,8,10,12,14,15.5和17 kn，对应模型速度分别为V=1.044，1.391，1.739，2.087 0，2.435，2.696和2.957 m/s等七个速度进行了数值仿真，并对相应速度进行了船体模型试验.仿真值和实验值结果见表3.

表3 各速度点仿真值和试验值对比

由表3可知，仿真值与试验结果的变化规律基本一致，二者数值的峰值差距约为3.5%，同时,根据实验现象可以看到船体周围兴波情况也相当一致，片体间的首尾兴波位置也基本相同，航速尾部兴波非常一致，见图3～4.所以使用Star-CCM+对高速双体船进行数值仿真是可行的.

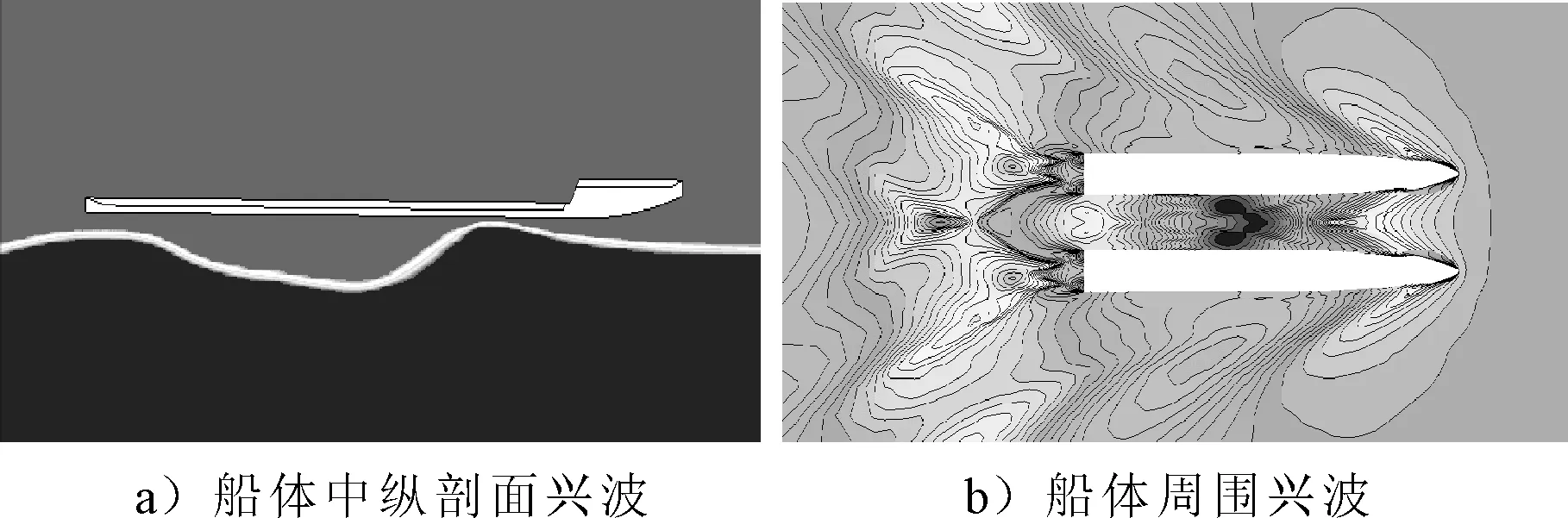
图3 数值仿真图

图4 设计航速数值仿真与模型实验船艉兴波对比

2 带翼型双体船数值仿真

2.1 单水翼数值仿真及结果分析

通过分析未装水翼的双体船进行模型试验和数值仿真结果，可以看出，在设计航速，数值仿真中片体间兴波位置与船模试验非常接近，艏艉兴波位置分别位于FR09和FR50处稍后.为使水翼得到较大升力，本文将水翼安装在波浪上升段，水翼位置安装于FR09与FR50处，水翼高度距基线100 mm.考虑到加工方便，本文采用对称型NACA0015，翼型宽度均为100 mm，翼型长度为200 mm.首先分别进行艏艉单翼型的数值仿真，再进行双翼型的仿真，水翼攻角分别为0°，2.5°，5°，7.5°和10°，数值仿真结果见图5.

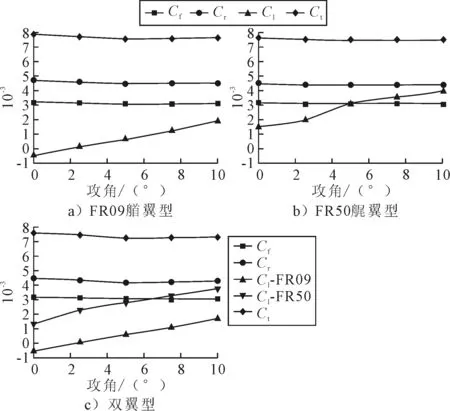
Cf-摩擦阻力系数；Cr -剩余阻力系数； Cl-升力系数；Ct-总阻力系数图5 设计航速不同攻角升阻力系数对比图

2.2 数值仿真结果分析

通过对数值仿真结果分析可见，仿真结果比较符合预期，有一定的规律性可寻：①翼型攻角变化对摩擦阻力影响较小；②三种翼型安装方式都在攻角5°左右时，剩余阻力较小，总阻力也较小，呈现最佳的阻力性能；③和未装翼型的数值仿真结果进行对比，设计航速首翼型最大减阻率为3.148%，尾翼型最大减阻率为4.612%，双翼型最大减阻率为6.657%，尾翼型较艏翼型减阻效果好，双翼型的减阻效果最佳；④翼型升力随攻角的增加而增大，同角度下尾翼型升力比艏翼型大.

3 双体船水动力翼模型试验

3.1 模型试验方案及试验结果

由于本次数值模拟只进行了设计航速处的仿真，为了探究水翼对高速双体船阻力在更多速度段的影响，同时也为了验证数值仿真的准确性，进行五组试验，选择0°，2.5°，5°，7.5°和10°五种攻角，在FR09和FR50处分别进行单翼型阻力试验，最后进行双翼型试验，试验速度点为V=1.043，1.391，1.739，2.087，2.435，2.696和2.957 m/s，试验结果见图6.

图6 不同攻角与无翼型阻力系数对比图

3.2 试验与数值仿真结果分析

根据模型试验结果可以看出，各工况下高速双体船总阻力在不同速度上呈现不同的变化，总要归纳为以下几点：①艏翼型状态下，低速段阻力增加较为明显，高速段翼型攻角为5°时有减阻效果，在V=2.957 m/s最大减阻率为0.939%，经实验过程观察发现，该种水翼安装方法对导致船体纵倾角过大，从而导致阻力的增加，没有达到数值仿真的减阻效果；②艉翼型状态下，低速度段阻力增加较为明显，在设计航速及以上航速状态下，模型总阻力出现下降的情况；在V=2.957 m/s时最大减阻率为2.141%；③对于首尾均安装水动力翼的情况，在低速段阻力有增大趋势，在高速段有减小趋势，在双水翼攻角均为5°时有较好阻力性能，速度V=2.957 m/s时最大减阻率为1.587%.

4 结 论

1) 通过对高速双体船三维建模，找到了一种快速高精度建立船体模型的方法，通过对型线图进行必要处理，并灵活使用CATIA中的宏命令，对复杂曲面添加辅助线对方式可以快速建立船体的3维模型.

2) 通过使用STAR-CCM+对高速双体船进行数值仿真，得到了比较理想的仿真结果，在设计航速状态时，误差为2.285%，在多个速度的仿真，最大误差仅为3.5%，同时该软件计算速度较快，相比于Fluent软件能够节约较多计算时间.

3) 通过对安装水动力翼的高速双体船进行数值仿真，初步了解了安装水动力翼对高速双体船的阻力性能和流场变化影响，发现翼型角度为5°时模型有较好的阻力性能，为模型试验起到了指导作用.

4) 通过进行高速双体船的无水翼模型阻力试验和安装水翼的多种工况下模型试验，得到了安装水动力翼后模型的阻力性能变化，发现在低速度段水翼的安装会增加船舶的形状阻力，从而引起总阻力增加，在高速段剩余阻力减小明显，从而使船舶总阻力减小，艉翼型安装方式下阻力减小较为明显，为最佳翼型安装方式.

5) 通过对比数值仿真和模型试验结果发现，阻力性能变化基本一致，艉翼型数值仿真与模型试验结果比较接近，艏翼型误差较大，双翼型结果误差在这两种情况之间，后续还需要进一步研究.