基于栅格化视觉的机器人路径优化研究

刘 梅

（河南牧业经济学院自动化学院 郑州 450011）

1 引言

路径最优规划是移动机器人系统中最重要的组成部分之一，分为点到点的路径规划和全覆盖路径规划［1］。点到点的路径规划是按照一定的评价标准，如工作代价最小、行走路线最短、行走时间最短等［2］，在其工作空间中找到一条从起始点到目标点的能避开障碍物的最优路径。主要包括全局路径规划和局部路径规划。在进行全局路径规划过程中，要找到一条从起点到终点的最优路径，首先进行整体环境建模，在此基础上通过搜索算法进行最短路径规划。环境建模方法通常有栅格法［3］、机器视觉法［4］和拓扑图法［5］等，在进行环境建模时通常采用其中一种或多种方法结合的建模方法。其中栅格法是最常见的建模方法，通过环境的栅格量化，机器人和障碍物位置可以用栅格的坐标来描述，编程易实现［6］。机器视觉法常用在点到点的路径规划中，通过标记障碍物顶点进行避障。A*搜索算法适合于全局路径规划和局部路径规划，是最常用的一种路径搜索算法［7］，通过计算代价值来进行路径搜索。本文针对点到点的全局路径进行算法设计和仿真，结合栅格法和机器视觉对环境进行建模，在栅格的基础上得到可视线形成可视觉化，通过减少有效可视点个数对视觉化进行改进，利用A*算法对所有可视线形成的路径进行代价计算，选择一条代价值最小的路径作为全局路径规划的最优路径。

2 环境建模

建立合适的环境模型是寻找最优路径的前提，这里在栅格化环境地图的基础上，机器人和障碍物可以量化在等大的单元格中，如果障碍物形状复杂，那么可以将障碍物量化在多个相邻单元格中，量化的障碍物和机器人用栅格顶点坐标分别表示出来。机器人初始位置置于起点处，以机器人为中心形成上、下、左、右、左上、左下、右上、右下的八连通栅格。连接机器人栅格顶点到障碍物外可视顶点形成可视线，这样从起点到目标点就有多条可搜索路径，然后结A*算法对这些连通的路径进行搜索，从而找到一条从起点到目标点的最短路径。

2.1 栅格化环境

将工作的环境区域进行栅格量化，得到一个m×m大小的环境区域，m为栅格区域边长。环境地图的每个栅格具有坐标属性cell(x。y)，用栅格的障碍物属性值来区分量化后的障碍物栅格和自由栅格。对自由栅格设置关联属性和搜索属性，自由栅格的八连通方向上的栅格关联属性值大的被搜索的概率大［8］。机器人初始位置设置在起点S用○表示，目标点G用◇表示，黑色是障碍物。图1所示是量化后的栅格模型。

栅格障碍物属性值设置：

其中，若为0时表示该栅格是自由的，判断该自由栅格八连通方向的栅格关联属性值，属性值大的可以被搜索；若为1时表示该栅格是障碍物栅格，不可以被搜索。自由栅格的关联属性值为大于0的正整数，关联值越大则搜索概率越大［9］，栅格搜索属性值初始值设置为

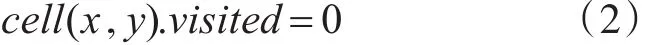
被搜索的栅格的搜索属性值：

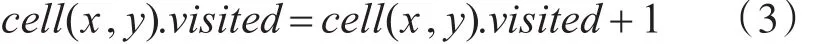
该栅格的关联属性值：

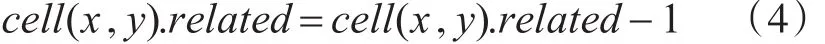
如果关联属性值大小一样，则机器人按照S→G方向覆盖上方、右上或者右边的栅格。

2.2 改进的视觉化

视觉化就是将所有量化在栅格中的起始点S(xs。ys)、障碍物顶点和目标点 G(xg。yg)用直线组合相连，同时要求三者之间的连线不能穿越障碍物，即直线是“可视的”［10］。给图中的边赋权值，构造图 G(V。E)，节点集V=V0∪(S。G)，E 为所有弧段(Pi。Pj)即边的集合，其中连接G中第i个和第 j个节点对接线端与任何障碍物均不相交，G(V。E)称作为可视图。节点V的选择可以决定构成的E的多少，从而决定算法所要搜索的路径。栅格化后的每个障碍物最多有三个可视点，可视点有外可视点和内可视点两种，能形成可视线的只有外可视点，连接图1中所有外可视点得到如图2所示，形成的可视线非常多。

图2 改进前所有可视点

为使起点到目标点的搜索路径减少，提高搜索效率，在这里提出一种基于栅格地图的改进的视觉化，可以大大减少可视线的数量，步骤如下：

Step1：以起点和目标点的横坐标和纵坐标所在直线相交，形成一个矩形区域，将包围在这个矩形区域内的障碍物作为形成可视线的目标，落在区域以外的障碍物不做考虑，如图3所示的矩形区域为机器人进行路径搜索的范围；

图3 改进后有效可视点

Step2：起点到终点的连线可以看做是一条有向的线段，这条线段所在直线可以表示为

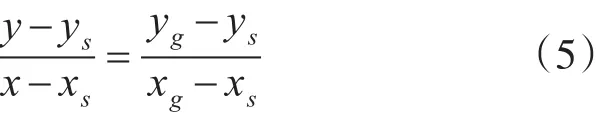
将直线方程标准化得到：

其中，A=yg-ys，B=xs-xg，C=xgys-xsyg。以这条直线为标准，无论连线是否穿越障碍物，计算矩形区域内所有从起点到终点方向的具有独立顶点的障碍物的外可视点 (xi。yi)，i=1。2。…到直线的垂直距离为

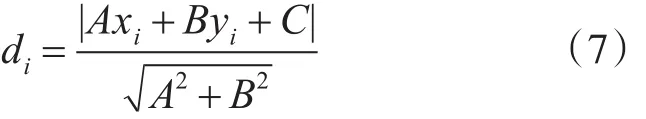
Step3：按照距离di从小到大的顺序将每个障碍物外可视点坐标分别进行排列，距离分界线越近的可视点期望值越大，每个障碍物的外可视点中选择一个距离最短的作为有效可视点；

Step4：将所有有效可视点进行连线，形成可视线，如图4所示。形成的可视线即为搜索范围。

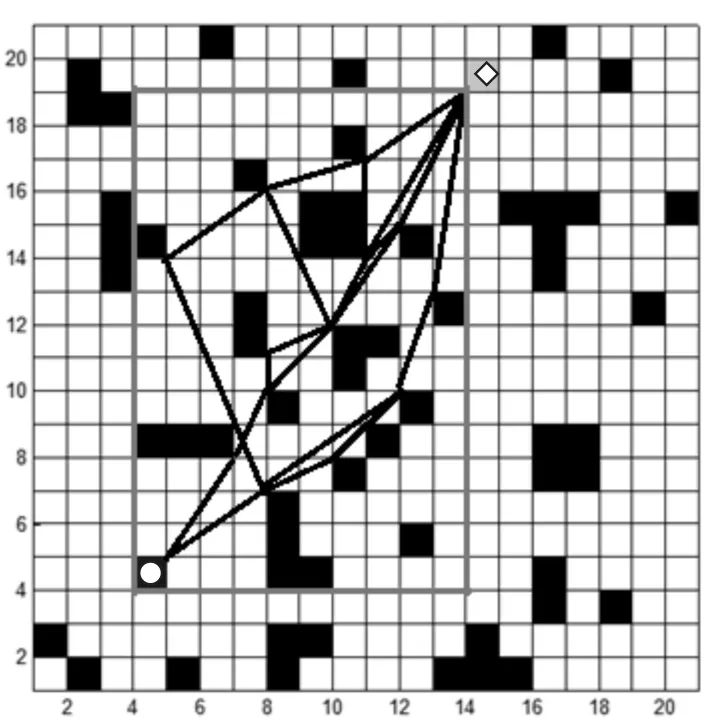
图4 可视线连通图

通过对可视图的改进，有效的可视点减少，按照已确定起点与目标点连线方向上，虽然障碍物类型繁多，分布区域杂乱，但是从起点到目标点的方向是一定的，如此就确定了有效可视点。距离起点终点方向连线距离远的障碍物顶点通过上述计算可知，距离代价值大，排除这些无效可视点后，大大减少了搜索的盲目性［11］。图2中改进前的可视点为48个，而改进后的可视点有15个，因此大大降低了搜索难度，提高了搜索效率。

可视点和可视线连接成有向图，组成了G=(V。E)，从起点S到目标点G，计算所有路径的长度并进行比较，最终选择一条最短的路径作为最优路径。这里利用A*算法进行搜索，确定最终的期望路径。

3 A*算法设计

3.1 基本思路

A*算法是在A算法基础上，对估价函数加上一些限制后得到的一种启发式搜索方法［12］。A*算法每次扩展所有可扩展节点中代价最小的节点。A*算法的关键是节点的代价 f(n)。设g(n)表示从搜索树树根扩展到达节点n的精确代价；h*(n)表示从节点n到达目标节点的最小代价，h*(n)是未知的。因此，从树根出发经节点n到达目标节点的最小代价为

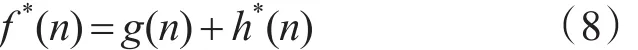
估价函数 f(n)与 f*(n)相比，g(n)是对 g*(n)的一个估计，h(n)是对h*(n)的一个估计。其中，g(n)≥g*(n)。 h(n)代替 h*(n)，但 h(n)≤h*(n)。综上，可以证明应用这样的估价函数是可以找到最短路径的。

在全局路径规划中，机器人从起点开始到节点再从节点到目标点的代价值用遍历的栅格总和来表示［13］，也就是机器人每覆盖一个栅格，成本代价就是从起点到节点的覆盖栅格数的累加，估计代价就是从当前节点到目标点的栅格数累加［14］。机器人在覆盖栅格的时候首先要判断目标栅格是否是自由栅格，然后判断这个自由栅格是否是关联性最大的栅格，与相关栅格比较如果关联值最大即作为覆盖栅格［15］。如果关联属性值大小一样，在机器人的八连通方向上则按照S→G方向覆盖上、右上或者右边栅格。

3.2 算法流程

具体的算法实现如下：

Step1：初始化所有节点S(N)放在OPEN表中，起点为S，目标点为G，估计代价取当前节点到目标节点的距离，即h(n)=dis(n。G)，搜索方向为起点到目标点方向；

Step2：判断OPEN表是否为空，是则转移到Step7，否则继续执行；

Step3：判断N是否是目标节点，是则转移到Step5，否则继续执行；

Step4：移出OPEN表中已搜索的节点N放入CLOSED表中，冠以编号n，且

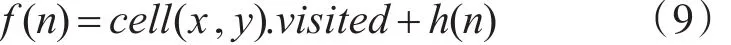
Step5：机器人沿着起点到目标点方向继续搜索下一个节点，判断目标节点cell(x。y).related值是否最大，是则利用式（3）、（4）转移到Step4，否则继续执行；

Step6：按照栅格八连通的方向和S→G方向覆盖上、右上或右边自由栅格。利用公式（3）（4）到下一个节点N，转移到Step3；

Step7：算法结束，退出程序。

4 算法仿真

基于栅格的改进的视觉化建模减少了可视点数量，结合A*搜索算法［16］，高效率的找到最短路径。通过基于栅格的改进视觉化的A*算法得到的最短路径，地图区域大小为20×20，其中○表示起点，也就是机器人初始位置，◇表示目标点，黑色表示障碍物，灰色表示搜索得到的最优路径，仿真结果如图5所示。

图5 仿真结果

从Matlab仿真结果可以看出，图中灰色路径表示规划的点到点的最短路径。基于栅格的A*算法需要扩展的点至少有两个，每一个点都要进行搜索，而且每一步都要进行路径代价估计比较然后选择一个节点继续进行扩展，如此反复，当障碍物可视点数量过多时，扩展点增多，相应的可搜索的路径增多，增加了搜索负担。在栅格表示法基础上采用改进的视觉化建立环境地图，减少了可视点个数，结合A*算法进行点到点的路径搜索，得到最后的最短路径，而且实际代价较低，提高了机器人的搜索效率。

5 结语

基于栅格表示的改进后的视觉化全局路径搜索是针对点到点的全局路径规划提出的算法，该方法通过对环境地图栅格化、点到点的可视线连通设计、点到点的路径搜索算法设计，实现了移动机器人从起点到目标点的最短路径规划，通过高效的环境建模方法，提高了算法的搜索效率。与一般的视觉化建模方法相比，基于栅格的改进的视觉化建模通过对障碍物所有可视点到起终点连线所在直线的垂直距离选择最短的可视点作为有效可视点，以此减少可视点个数，相应可供选择搜索的可视线减少，再结合A*搜索算法对所有路径进行判断，最终得到一条代价最小的路径作为全局路径规划的最短路径。仿真实验结果表明该方法具有可行性和有效性。