基于高斯混合模型的改进GVF-Snake运动目标检测算法

卢 毅 李文新

（兰州空间技术物理研究所 兰州 730000）

1 引言

目标检测是图像分析和计算机视觉当中最重要的任务之一。虽然在该领域已经存在很多方法，但是由于图像的多样性和复杂性，设计一个鲁棒性好且有效的检测算法仍然是一项非常有价值的课题［1～2］。

Snake主动轮廓模型是由Kass等提出的，该模型提取出的轮廓与目标真实轮廓能够非常精确的吻合，这使得Snake主动轮廓方法受到广泛使用。在Snake主动轮廓模型中，Snake曲线被设定为一条闭合曲线，目标检测的过程是一个由外部约束力引导的能量最小化过程，并且该过程同时受到图像力的影响，这使得Snake曲线能够被推向图像中的目标真实边缘处［3～4］。但是Kass等提出的Snake主动轮廓模型在拓扑结构上不灵活的缺陷使得snake主动轮廓模型不适用于目标边缘有明显凹陷和图像中有多个待检测目标的检测任务。而且在图像中噪点较多的情况下，Snake主动轮廓模型的检测效果受影响较大［5］。

GVF-Snakes模型构造新的能量函数，使用变分法求解该能量函数最小值，即得到关于图像本身的稠密矢量场，从而得出新的外部力。而该能量函数最小化的过程是借助一对不相关的偏微分方程求解完成的，这个过程扩散了图像中关于灰度的梯度矢量。

GVF-Snake模型中，即使初始Snake曲线距离目标真实边缘较远，Snake曲线仍然能够被GVF场牵引至目标的真实边缘处。但是GVF-Snake只使用灰度梯度作为边缘分布图，并未使用图像中隐含的像素统计信息。本文使用高斯混合模型建模方法对GVF-Snake算法进行改进，利用图像中包含的统计学信息进行目标检测。

2 Snake算法

2.1 传统Snake算法

传统Snake算法中的Snake曲线，也被称为主动轮廓，指的是一个在内部约束力和外部约束力控制下变化的闭合连续曲线［6］。

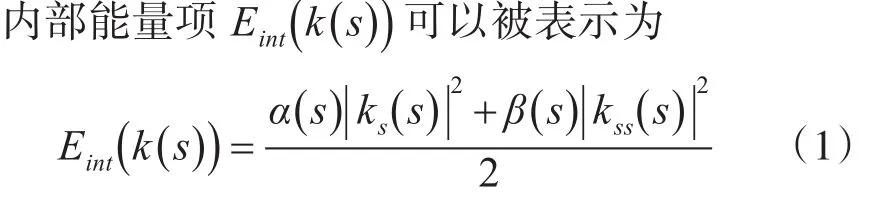
其中k(s)=(x (s)。y(s))是Snake的曲线表达形式，s是曲线的参数，ks(s)和kss(s)分别表示曲线关于s的一阶偏微分和二阶偏微分。α和β分别为控制曲线的张力和平滑程度的影响因子。

外部能量函数Eext(k (s) )来源于图像数据本身，它用于将Snake曲线牵引向图像的线条、边缘和末端处，也就是说它使得Snake曲线最终趋向于灰度变化剧烈的分界处。全部的图像能量可以被表达为一个加权的能量和。

通常使用的外部能量有以下两种：

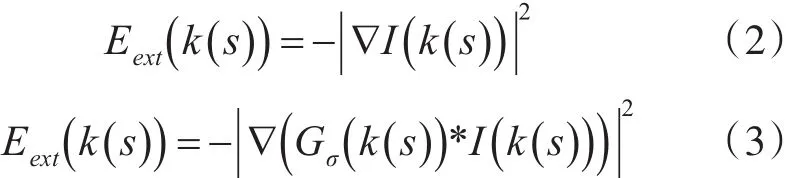
综上所述，Snake模型能量函数如下式，当下述能量函数积分式取得最小值的时候，即取得最佳轮廓。

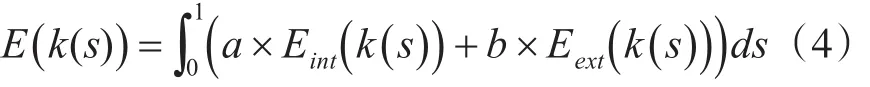
而Snake模型通过改变影响因子a和b的大小，控制内部力和外部力对于能量积分求最小值的影响程度。

2.2 GVF-Snake算法

梯度矢量流snake是一种改进的主动轮廓模型，它利用矢量场W(k (s))=(u (k (s))。v(k (s) ))最小化能量函数［7］。矢量场 w(s)=(x (s)。y(y) )通过最小化下述能量公式得出：

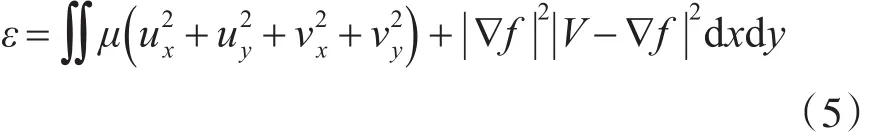
3 高斯混合模型（GMM）

高斯混合模型是一种密度模型，其中包含有多个高斯函数成分［8～9］。这些函数通过不同的影响因子相结合以形成一个多重概率分布，从而可以更加准确地描述具有复杂变化的背景

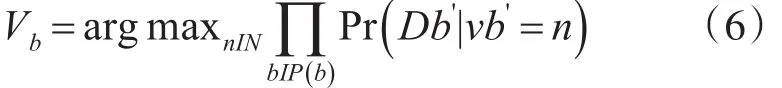
b区域。它应该被定义为一组以b为中心的更大的T×T的子图块。Db被标记为与子图块有关的数据，Vb=N是b的分类。这个分类过程可以通过基于以下公式完成：在此处，P()b中所有的子图块都取最大的可能性。这降低了分类过程的计算时间。与任一子图块有关的Db数据被记为特征向量x→。则包含x→的可能性就可以被表述为一个关于混合高斯密度公式的凸组合：

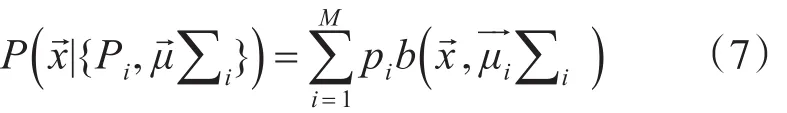
对于一个自然类含有多个子类的情况，高斯混合模型是一种行之有效的分类方法。通过使用高斯混合模型获得图像中某一自然类的概率分布，这种描述方法具有很好的准确性［10～11］。

4 改进的GVF算法

本文提出的改进方案首先使用高斯混合模型对图像进行建模，得到各像素属于目标的可能性如下：

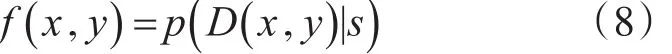
使用得到的概率分布代替GVF场计算过程中的边缘分布图，计算的到新的GVF场。利用变分法通过求解如下欧拉方程可得到梯度矢量流w的解：

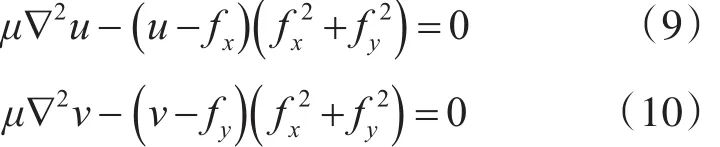
式中，∇2为拉普拉斯算子，将上式进行离散化处理，可得到求解GVF场两个分量的迭代公式的过程如下。把u和v看作关于时间的函数，这利用变分法得到的欧拉公式化为广义扩散方程：

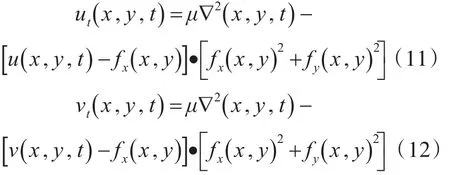
因为上述两式中的u和v是相互独立的，所以可以分别当作两个独立的关于u和v的偏微分方程来处理。

设：

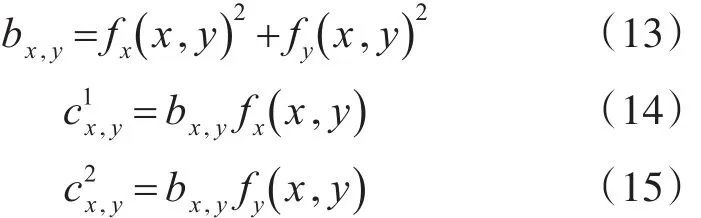
则广义扩散方程简写为

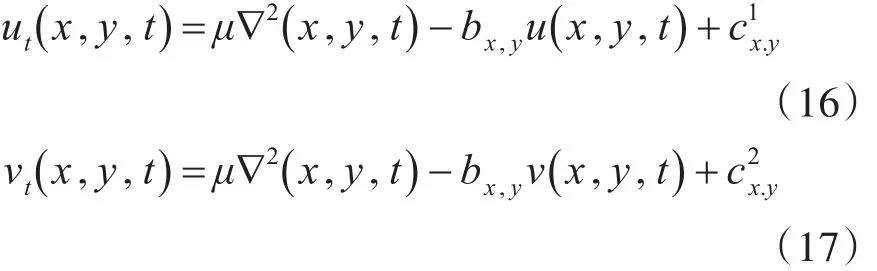
利用中值差分来计算 fx和 fy，在数学概念上数字图像就是离散的点值谱，也可以叫二维离散函数，x和y都是以1为间隔进行取值的正整数，即Δx和Δy的值都为1。之后的公式推导中，我们分别使用i，j和和迭代次数n来代替x，y和t，任何一次迭代的时间步长值为Δt。代入中值差分得到：

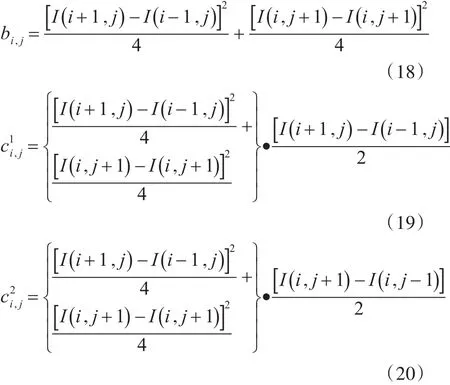
同时利用离散差分方式对偏微分进行近似处理，得到迭代解结果如下：

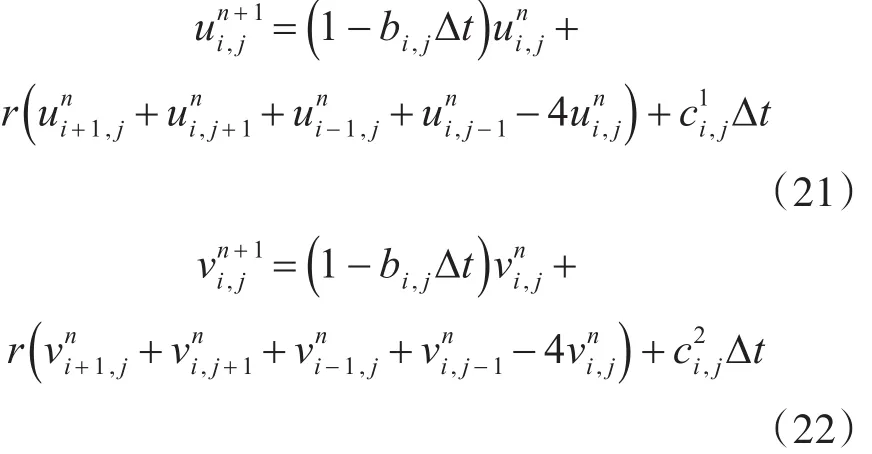
分析公式可以看出，在使用该迭代公式求解的过程中，每进行一次迭代，前一次迭代结果的和都会参与到周围四个像素的下一次迭代计算中，从而将该像素的影响扩散出去。假设该迭代过程进行了n次迭代，则任何一个像素的信息都会传递到n个像素距离之外，从而影响以该像素为中心，n为距离的范围内的所有GVF场向量。将改进后的GVF场作为Snake能量函数的外部能量项，并求解能量函数的最小化即可得到目标检测结果。

5 实验结果

为验证本文提出的改进GVF-Snake算法的有效性，选取两组图像序列进行目标检测实验。图一中使用的图像序列是关于道路上汽车目标的检测实验，分辨率为360×340，用于验证算法在目标大小有变化的情况下检测结果的有效性。图二中使用的图像序列是关于活动的人物目标检测，分辨率340×340，用于验证算法在目标形状有变化的情况下检测结果的有效性。在试验中，为了获取用于Snake曲线收敛运算的初始轮廓，需要对第一帧图像和混合高斯模型背景建模的结果做差分运算，并将差分结果做图像形态学预处理得到。

从图1和图2的检测结果可以看出，由于本文提出的改进方法为GVF-Snake检测算法引入了GMM的背景统计，从而排除了复杂背景对于目标检测过程的干扰，使得活动轮廓最终能够收敛到目标的真实边缘处。综合来看，本文提出的算法对于目标大小的变化以及目标形状的变换都表现出较好的适应性。

图1

图2

6 结语

本文基于GMM背景建模的方法，修改了GVF-Snake算法外部能量项，增强了GVF-Snake算法对于复杂背景下运动目标的检测性能。同时，通过对图像的GMM背景建模，可以自适应地利用差分图像获得较好的初始轮廓，增强了算法的自适应能力。实验结果也表明，本算法对于复杂背景下，目标形状或大小有变化的目标检测都能给出较好的结果。下一步工作是将该算法的使用范围从灰度图像扩展到RGB彩色图像，充分利用RGB空间丰富的色彩信息进一步提高算法的检测效果。此外，将算法的运行平台移植到FPGA以提高算法的运行速度也是另一方面的工作方向。