基于修正预测状态的移动机器人跟踪定位算法

袁铸靳果

（河南工业职业技术学院 南阳 473009）

1 引言

在目标的精确定位中，多传感器信息融合技术被广泛应用。而作为多传感器信息融合技术中的重要组成部分的卡尔曼滤波，已被广泛应用于交通、导航系统和航空航天的定位中［1～4］。卡尔曼滤波对处理线性系统或多输入输出的平稳系统的系统噪声非常有效，能够实现无偏最小方差估计［5～8］。但对非线性、结构复杂的系统，处理效果非常差。而对于移动机器人的跟踪定位系统来说，其状态模型和量测模型大多是非线性的，所以使用卡尔曼滤波效果有限，本文基于在二维平面上做匀速运动的移动机器人，提出一种改进算法——基于修正预测状态的移动机器人跟踪定位算法来提高目标定位精度。

2 Kalman滤波

在对跟踪问题研究中，要想获取目标的运动参数，用一定的量测手段测量出运动目标的运动状态就成为必须。但量测值中包含量测噪声，而且也有可能只是系统部分状态的线性组合。1960年，卡尔曼提出了卡尔曼滤波器［9］。卡尔曼滤波以误差方差最小为准则，是一种线性、无偏的最优估计算法［10］。卡尔曼滤波方法采用递推滤波方式，根据获取的量测数据中递推方程递推给出新的状态估计。卡尔曼滤波方法采用递推滤波方式，由获取的量测数据，根据递推方程递推给出新的状态估计，所以初始信息是否准确并不重要适用于平稳和非平稳的多维随机过程估计。

本文研究移动机器人的跟踪定位，其系统方程可表示为

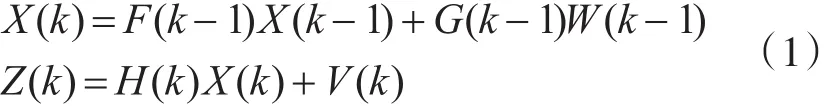
假定目标的状态方程和量测方程如式（1）所示，并假定已知目标在k-1时刻的状态变量X(k-1)的状态估计值 X^(k-1/k-1)，协方差矩阵P(k-1/k-1)，那么卡尔曼滤波算法的数学表达式可表示如下：

1）状态预测值

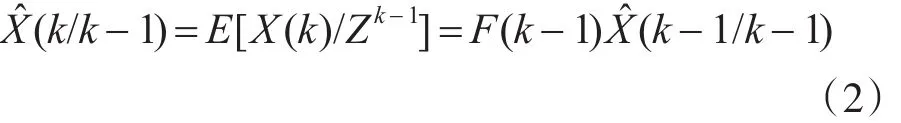
其中，Zk-1={Z(j)，j=1。2。…。k-1}为从1到k-1时刻量测向量的总合。

2）状态预测协方差矩阵

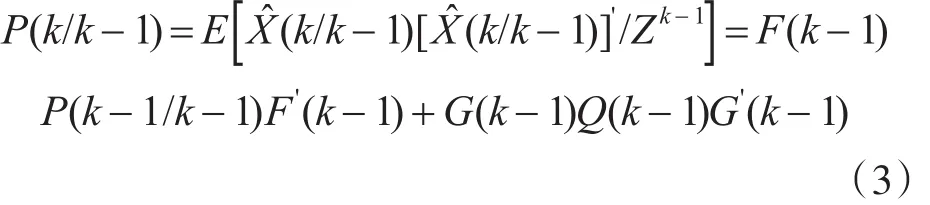
3）量测预测值

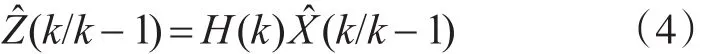
残差向量可以定义为

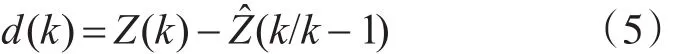
4）残差向量协方差矩阵

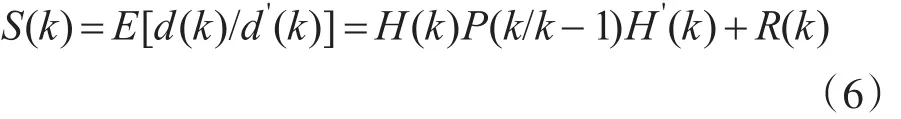
5）增益矩阵

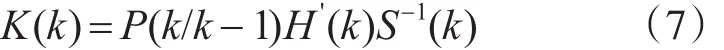
6）状态估计值

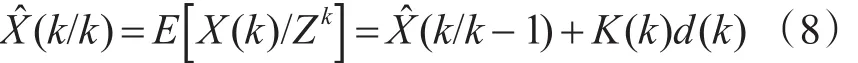
7）状态估计值协方差矩阵

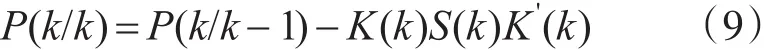
由上面公式可知，该算法以给定的初始估计值X^(0/0)和其协方差矩阵P(0/0)为出发点进行递推。

3 基于修正预测状态的移动机器人跟踪定位算法

卡尔曼滤波算法的滤波过程本质上是对目标状态观测值不断预测和修正的过程，所以当移动机器人运动距离的变大，系统的累积误差也必然会随之增大，为了保证移动机器人跟踪定位的精度，引入修正预测——基于移动机器人自身的驱动力和与地面的摩擦力所得到的位置预测。

根据动力学知识可知，若要使移动机器人保持匀速运动，那么必须保持力的平衡，即机器人与地面产生的摩擦力和机器人自身的驱动力保持平衡。那么加速度a和地面摩擦力 f的关系可表示为

其中，k为常系数，m为移动机器人总质量。

将求得的位置预测值乘以系数0.5与卡尔曼算法中的预测值乘以系数0.5求和，即为最终的预测位置。

4 仿真研究

假设移动机器人在（-100，0），（60，1800）的二维平面上作匀速运动，且初始位置为（100m，200m），沿x轴方向的运动速度为2m/s，沿y轴方向的运动速度为20m/s，环境中传感器扫描周期T为1s。移动机器人跟踪定位的仿真结果如图1～2所示。

图1为改进算法前后卡尔曼滤波的轨迹跟踪图，图2为改进前后卡尔曼滤波的误差对比图；由图2可知，改进后的算法有效地减小了系统的定位误差，并且定位精度明显提高。

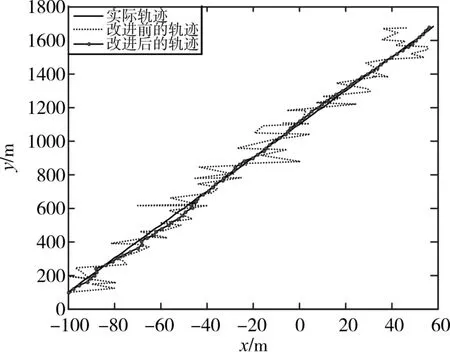
图1 改进算法前后卡尔曼滤波的移动机器人跟踪轨迹图

由表1可知，引入修正预测状态——移动机器人自身的驱动力和与地面的摩擦力的预测状态，并乘以系数，与卡尔曼滤波结果进行融合，那么移动机器人跟踪定位算法运算时间比原算法的时间短。由表2可看出，改进后的算法与原算法相比定位误差明显减小。

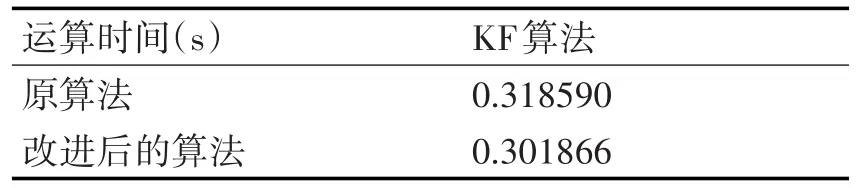
表1 改进算法前后的运算时间

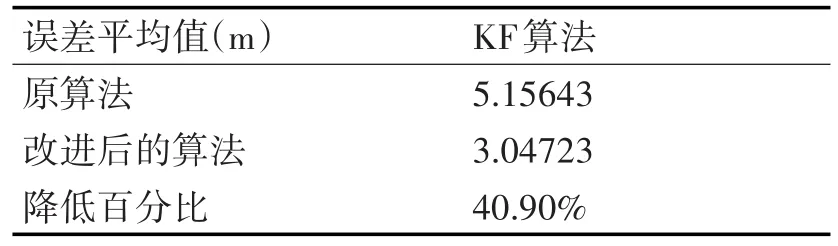
表2 改进算法前后的误差平均值比较

5 结语

本文针对移动机器人在二维平面内的匀速运动，通过引入修正预测状态——由移动机器人驱动力和与地面摩擦力所预测的机器人位置状态，并转化为状态估计的一步预测，与原算法中的一步预测相结合形成跟踪定位系统中修正后的预测，减小了跟踪定位系统的累积误差，提高了系统的定位精度，并且避免了滤波发散问题，仿真结果也表明了本章方法的有效性。