基于稀疏分解的空间目标双基地ISAR自聚焦算法
2018-08-29韩宁李宝晨王立兵童俊郭宝锋
韩宁,李宝晨,王立兵,童俊,郭宝锋
1.军械技术研究所,石家庄 050003 2. 陆军工程大学 科研学术处,南京 210014 3. 中国人民解放军63961部队,北京 100012 4. 陆军工程大学石家庄校区,石家庄 050003
双基地逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)因其具有良好的“四抗性能”,且成像不受目标运动方向限制,已逐渐成为国内外的研究热点[1-6]。双基地ISAR作为空间目标监视的一种重要手段,具有成像距离远(发站靠前布置)、可实现目标多姿态观测等优点,是未来空间目标监测与识别的一个重要发展方向。
目前,对双基地ISAR的研究,主要集中在全极化成像[7]、旋转运动的补偿方法[8-9]、双基地ISAR图像重建[10]、双基地ISAR图像的快速生成[11]、双基地ISAR三维成像[12-13]等方面,对双基地ISAR的理论研究还有待进一步丰富与完善。而且,大多数研究都基于成像期间双基地角恒定不变的假设,没有研究双基地角时变对成像的影响。针对双基地角时变对成像的影响这一问题,文献[14]主要研究了双基地角对成像自聚焦的影响,并利用循环迭代和初始相位误差的高精度估计与校准来完成双基地角时变下的自聚焦。但该方法性能优劣受循环迭代次数的影响较大,为了得到聚焦精度较高的二维ISAR图像,通常需要反复多次的循环迭代才能完成,且在迭代后期,图像的聚焦度并未有明显提升。针对双基地角时变下的自聚焦问题,本文基于相位建模、参数估计、高阶相位补偿的思路,研究提出了一种利用稀疏分解算法估计二次项系数完成相位补偿的自聚焦算法。
1 空间目标双基地ISAR成像原理
以平稳空间目标为研究对象,双基地ISAR的成像原理模型如图1所示。
图1中:T为双基地雷达的发射站;R为接收站;TR为双基地雷达基线;Rt0、Rr0分别为观测时刻目标相位中心距发射站和接收站的距离;Rt1、Rr1分别为目标运动到下一时刻时,目标相位中心距发射站和接收站的距离;Rv0为目标运动方向矢量;Ci为目标上的任一散射点;Ei为该散射点在观测起始时刻目标相位中心与收发双站雷达确定的平面内的投影;RtCi0、RrCi0分别为散射点Ci在观测时刻距发射站、接收站雷达的距离。
在较短的成像积累时间内,平稳目标在空间中的姿态是平稳的,为描述散射点在空间中的位置,建立以目标散射中心为原点的目标惯性坐标系,具体方法为:以观测起始时刻目标双基地角平分线延长线方向为y轴正方向;以观测起始时刻目标轨道与目标双基地角平分线构成平面内y轴的法线为x轴,x轴正方向与目标运动方向一致。该坐标轴指向不随目标的运动改变,因此该坐标系下目标散射点距离的变化包含了目标的平动和相对转动。为便于分析目标转动情况,建立目标的双基地角平分坐标系x′O′y′,该坐标系的y′轴为双基地角平分线延长线方向,并随着目标的运动和双基地角平分线指向的改变而改变;x′轴则是xOy平面内y′轴的法向。因此,x′O′y′坐标系与xOy坐标系间的相对转动角直接反映了目标在观测时间内的相对转动情况。
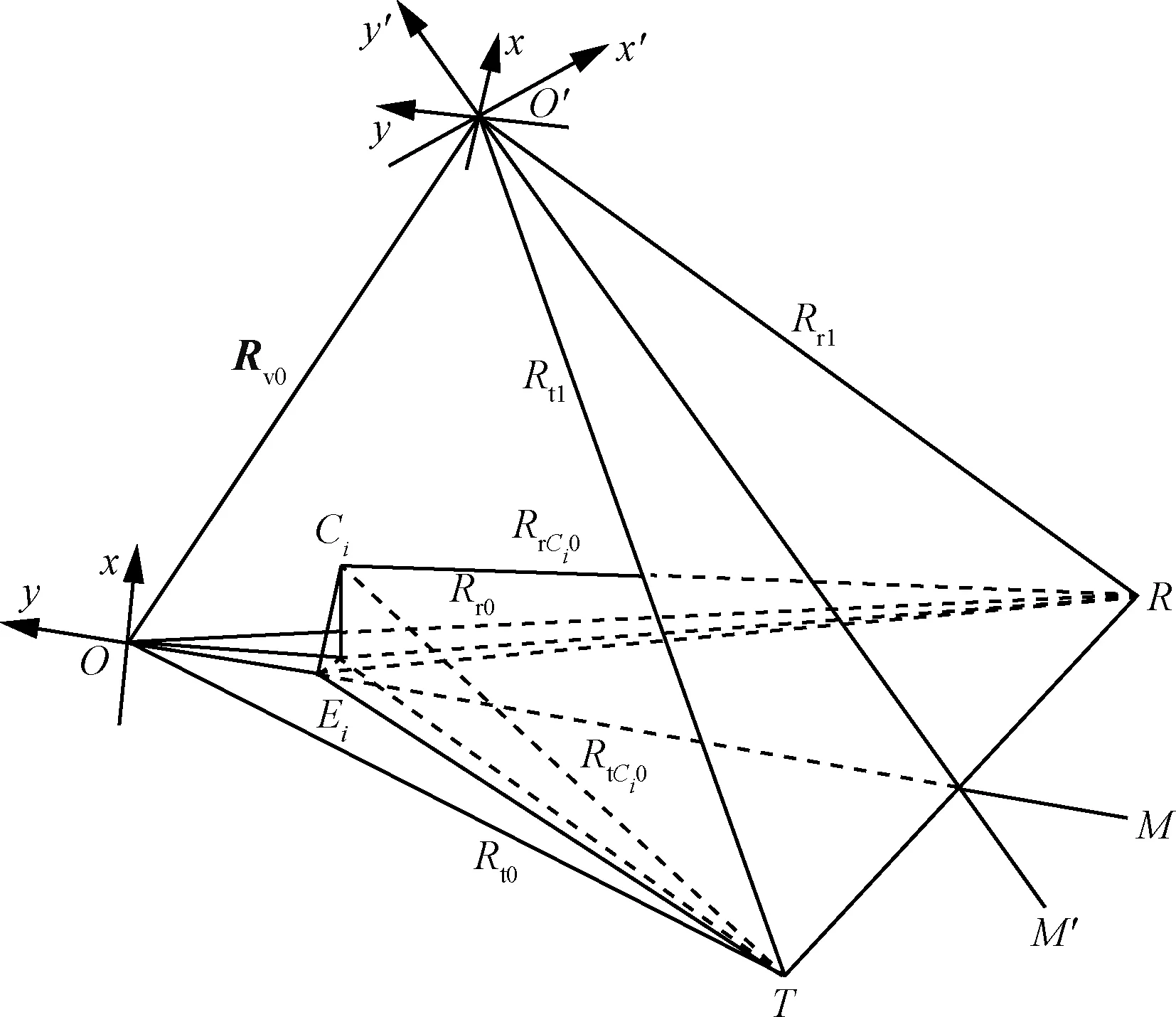
图1 双基地ISAR成像原理模型Fig.1 Principle model for imaging of bisatic ISAR
在建立以上坐标系的基础上,假设雷达发射如式(1)所示的线性调频信号
(1)
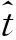
假设双基地雷达理想同步,即不存在时间、空间、频率的同步误差,且成像期间双基地角恒定不变,则中频采样下变频后得到的散射点基频回波如式(2)所示:
(2)
式中:σCi为散射点Ci的散射系数;c为真空中的光速;RCi(tm)可表示为
RCi(tm)=Rref(tm)+Rrotitm≈
(3)
式中:Rref(tm)为目标散射中心的平动分量;Rroti(tm)为目标上散射点Ci的转动分量;θCi为散射点Ci方位矢量与xOy坐标系中x轴正向的夹角;ψ(tm)为成像期间双基地角平分线的转动角度;β0为成像期间的双基地角;ri为散射点Ci到目标散射中心的距离。
对式(2)进行脉冲压缩,即可得到目标的一维距离像为
(4)

由式(3)和式(4)可以看出,双基地ISAR回波中散射点到收发双站的距离依然可以分解为平动与转动项之和的形式,在完成包络对齐之后,将平动和转动导致的相位项统一建模,而后进行二次相位项补偿即可实现自聚焦,随后完成方位压缩即可得到目标的二维ISAR图像[15]。
2 双基地角时变对自聚焦的影响机理
当成像期间双基地角随慢时间变化时,式(3)可表示为
(5)
式中:β(tm)为成像期间双基地角随慢时间tm变化。
为了分析双基地角时变对散射点回波的影响,基于泰勒展开的方法,将β(tm)按式(6)进行展开
β(tm)≈β(0)+β′(0)tm
(6)
式中:β(0)为β(tm)在零时刻的双基地角;β′(0)为β(tm)在零时刻的一阶导数。此时,半双基地角的余弦可做如下近似:
K0+K1tm
(7)
式中:K′(0)为半双基地角余弦相对慢时间的变化率;
(8)
(9)
其中:K0、K1分别为时变半双基地角余弦的常数项及线性变化项。
目标相位中心的平动距离项Rref(tm)为
Rref(tm)=Rref(t0)+vreftm
(10)
式中:Rref(t0)为目标散射中心在成像初始时刻至收发双站的距离;vref为目标散射中心在成像期间相对收发双站的运动速度。
此时,将式(8)~式(10)代入式(5)进行化简可得
2yiK1tm+2xiψ(tm)K0+2xiK1ψ(tm)tm=Rref(t0)+2yiK0+(vref+2yiK1+2xiK0ω)tm+
(11)
式中:ω为双基地角平分线的转动角速度;xi、yi分别为散射点Ci在xOy坐标系中x轴与y轴上的坐标;η0、η1和η2分别为散射点Ci转动距离项的常数项、一次线性项和二次项。
由式(11)可以看出,双基地ISAR成像中,受双基地角时变的影响,散射点成像所需的相位项中产生了二次项,必须对该二次相位项进行补偿,否则会导致二维ISAR图像的散焦。
3 基于稀疏分解的自聚焦
分析式(11)可以看出,若能利用合适的方法估计出二次项的系数η2,然后构造如式(12)所示的补偿相位项:
(12)
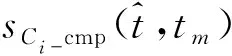
exp(-j2πf0η0)exp(-j2πf0η1tm)
(13)
式中:第一个相位项为常数项,不影响自聚焦及二维成像;第二项为成像所需的线性相位项。由式(13) 可以看出,经过补偿后的一维距离像数据中,已不包含会造成图像散焦的二次相位项。因此,通过估计参数η2并据此构造补偿相位项完成二次项补偿的方法,可实现双基地角时变下的自聚焦。
稀疏分解的目的是从一个过完备的矢量集(或函数集)中选择尽量少的元素来表示已知信号,当构造出与信号特征相匹配的冗余基时,稀疏分解能挖掘出信号内部的精细结构,极大地提高变换域的分辨能力,目前,稀疏分解已广泛应用于雷达及光学成像、信号去噪、信号参数估计等领域[16-20]。本文利用稀疏分解的高分辨能力,构建符合距离分辨单元信号特征的冗余基,利用稀疏分解完成二次项系数的估计。
3.1 稀疏词典的构建
为便于论述,重写散射点经脉压后的回波为
(14)
式中:A为不同距离分辨单元内复数形式的回波强度;N为成像所需的积累脉冲数;Ttrs为发射站雷达的脉冲重复周期。构造冗余基为
(15)
式中:K为冗余基因子数
(16)
其中:ai1、ai2分别为对η1、η2进行高精度划分的第i组冗余基参数因子。此时,sCi_T在该冗余基Φ上可表示为
sCi_T=Φa
式中:a为不同散射点对应的复回波强度,其非零元数个数由散射点个数决定。在高频区,目标回波可近似认为是来自若干稀疏分布的离散点散射回波的集合[21],因此,向量a可在冗余基Φ上对信号sCi_T进行稀疏表示,只需用合适的稀疏分解算法估计出a,即可根据系数a及其在冗余基中对应的冗余基因子,构建补偿相位项完成二次项的补偿。
3.2 二次项系数的稀疏估计
在各类稀疏分解算法中,基于正则化的迭代算法可避免全局贪婪寻优算法中一步错步步错的问题,故得到更加广泛的应用。基于一般性稀疏度量函数,文献[22]研究了推广的正则化欠定系统聚焦求解(FOCal Underdetermined System Solver,FOCUSS)算法,该算法提供了较为丰富的稀疏性度量函数的选取方法,可根据不同的应用背景选取稀疏度量函数,降低算法运算量,故本文使用该稀疏分解算法完成参数估计,其迭代过程为
(18)
式中:x(k+1)为第k+1次迭代的稀疏表示系数;Wk为与选取的稀疏性度量函数有关的矩阵;A为冗余基;λ为与噪声水平有关的正则化参数;当λ→0+时,即观测噪声为0时的稀疏解。
3.3 算法基本步骤
以上分析基于单散射点回波进行,当某个距离单元内有多个散射点时,只需按照所有散射点中可能的参数取值范围对η1、η2进行适当划分,即可构建出相应的冗余基,以使回波信号在该冗余基上具有稀疏性。
综合以上分析,基于稀疏分解的自聚焦算法步骤为:
步骤1利用最大互相关法完成一维距离像的包络对齐。
步骤2依据目标尺寸及其运行轨道等先验信息,对η1、η2进行高精度划分,并按照式(15)和式(16)构建冗余基Φ。
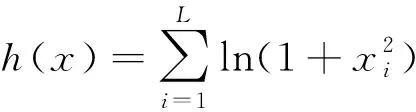
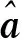
以上算法针对距离单元内只存在一个散射点的情况,当某个距离单元内存在多个散射点时,因不同散射点的二次项系数不仅与成像初始时刻的半双基地角余弦有关,而且还受散射点的横坐标影响,此时需对算法进行适当调整。
假设某个距离单元内存在两个散射点C1、C2,对应其估计出的二次项系数分别为η2C1、η2C2,此时,按照算数平均的方法构造补偿相位项为
(19)
当某个距离单元内存在更多个散射点时,构建补偿相位项的方法与式(19)类似。
3.4 算法关键参数的选取
在使用推广正则化FOCUSS算法进行稀疏分解时,若原始信号中不包含噪声,在迭代过程中只需逐次增大惩罚因子M,当分解精度满足预先设定的精度要求时即可得到精确的稀疏分解结果。若原始信号中包含噪声,则需首先选择正则化参数λ,然后用1/λ作为惩罚因子M,基于该惩罚因子进行稀疏分解得到噪声环境下的稀疏表示系数。正则化参数λ需在稀疏解的稀疏度和信号表示误差之间折衷考虑,正则化参数选取的好坏直接决定了稀疏分解结果的稀疏度和对原始信号的逼近程度。目前,关于正则参数的选择,主要有先验策略和后验策略两类,先验策略最早由Tikhonov提出,正则化参数在正则化过程之前就已经确定。先验策略涉及到“最优正则参数”是否存在以及如何确定的问题,故应用较少,更具备理论研究上的价值。后验策略与信噪比是否已知有关。当噪声水平已知时,主要有Morozov偏差原理和Arcangeli准则;当噪声水平未知时,主要有拟最优准则、L-曲线准则、交叉验证、广义交叉验证准则等。

4 仿真实验与分析
仿真双基地雷达参数如表1所示,利用频域脉压的方法完成距离维成像,用最大互相关法完成包络对齐。自聚焦分别用本文研究的基于稀疏分解的自聚焦算法和相位梯度自聚焦(Phase Gradient Autofocusing,PGA)算法进行,方位向压缩通过傅里叶变换完成,空间目标的初始两行轨道根数格式如表2所示,按照文献[24]的算法完成回波模拟。
仿真用目标的三维散射点模型如图2所示,目标尺寸设定为30 m×20 m×5 m,结合初始轨道根数,对1阶系数的高精度划分因子为0.1,2阶系数的高精度划分因子为0.05。图3为PGA算法和本文算法得到的目标成像结果。
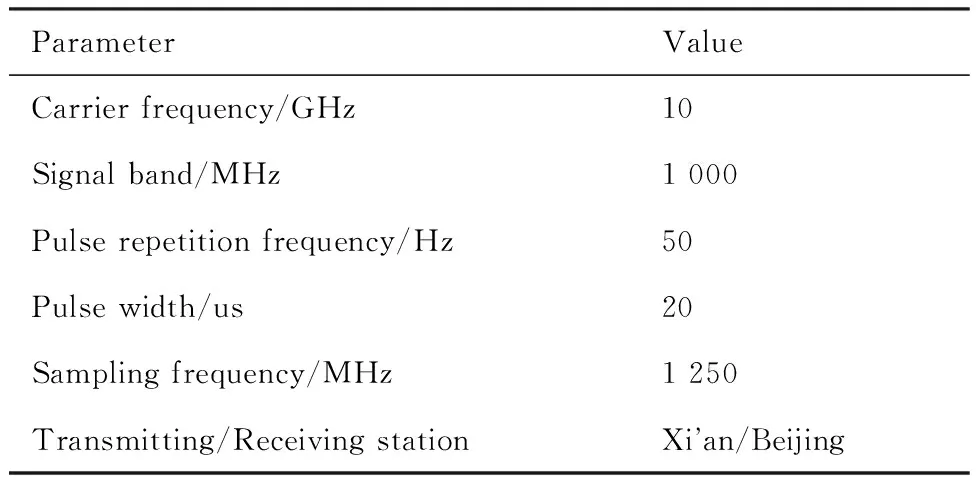
表1 双基地雷达主要参数Table 1 Main parameters of bistatic radar
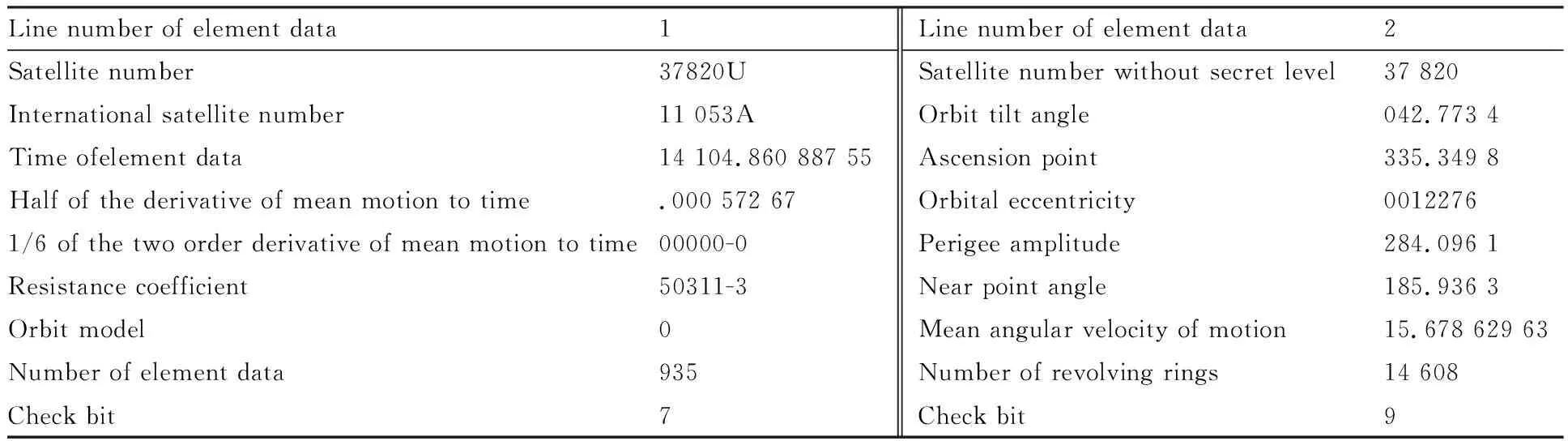
表2 仿真用两行轨道根数格式Table 2 Two Line Elements(TLE) format for simulation
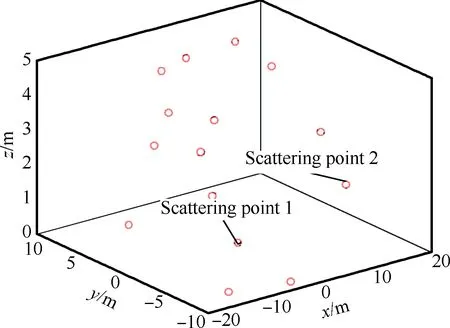
图2 目标散射点模型Fig.2 Model for target scattering point
图像对比度可作为评价图像质量的指标,图像对比度越大则图像的聚焦度越高,故本文选取图像对比度作为评估不同自聚焦方法性能优劣的指标之一,其定义为[25]
(20)
式中:Cimag为图像对比度;I(x,y)为复图像的幅度;A(·)为图像在整个成像平面(x,y)上的幅度平均。
按照式(20),表3给出仿真100次时,用本文

图3 目标成像结果Fig.3 Results of target imaging
算法和PGA算法进行自聚焦时统计得出的图像对比度平均值,此外,该表中还给出了图像散射点的距离向和方位向3 dB主瓣宽度的平均值。

表3 图像对比度,散射点距离和方位向3 dB主瓣宽度统计结果Table 3 Statistical results of image contrast and 3 dB mainlobe width in range and azimuth
从表3可以看出,用PGA算法和本文算法完成自聚焦所得的图像中,距离向的主瓣宽度基本一致没有明显变化。在方位向,通过统计成像期间双基地角平分线的转动角度,可计算出方位向理论分辨率为0.317,相对而言,本文算法使图像散射点方位向分辨率偏离理论分辨率的程度更低,具有更优的聚焦效果。
从式(11)可以看出,因成像期间双基地角随时间变化,故二次相位项系数与散射点横坐标有关,但因目标体积的量级远小于目标与雷达的距离,因此该部分相位相对于平动相位误差较小,而在利用PGA算法进行自聚焦时,在迭代的初始部分(前150次迭代)主要完成平动相位误差的补偿,二维图像的对比度会有较大提升,但若继续进行迭代,图像对比度的提升有限,无法从根本上补偿与散射点横坐标有关的相位误差,图4给出了二维ISAR图像的图像对比度随PGA算法迭代次数的变化趋势,从图中可以看出,当迭代次数大于150次时,图像对比度虽然总体上呈继续提高的态势,但其提高比率较低,这与本段前半部分的理论分析一致,故在图3和图4的成像结果对比中,也用迭代150次的成像结果与本文算法进行对比。
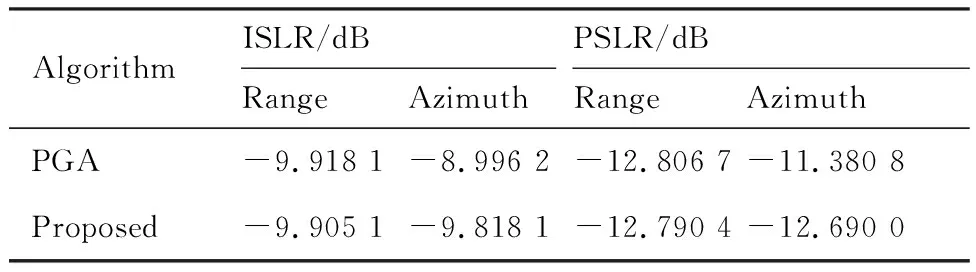
积分旁瓣比(Integral SideLobe Ratio, ISLR)和峰值旁瓣比(Peak SideLobe Ratio, PSLR)也常用于表征雷达成像性能,表4给出了两种自聚焦算法对应的ISLR和PSLR指标,从表中可以看出,在距离向上,两种自聚焦算法并无明显区别,但在方位向上,本文研究的自聚焦算法优于常用的PGA算法。
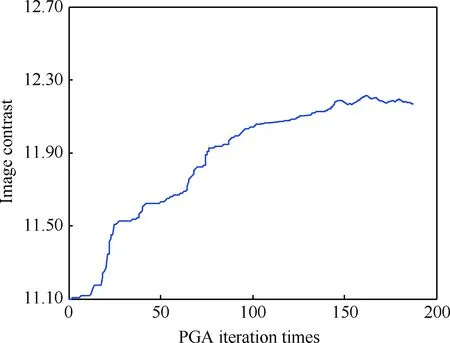
图4 PGA算法迭代次数与图像对比度的对应关系Fig.4 Corresponding relation between iteration times of PGA algorithm and image contrast
表4 散射点ISLR、PSLR参数统计
Table 4 Statistical results of ISLR and PSLR of scattering point
AlgorithmISLR/dBPSLR/dBRangeAzimuthRangeAzimuthPGA -9.918 1-8.996 2-12.806 7-11.380 8Proposed-9.905 1-9.818 1-12.790 4-12.690 0
为了更加直观地说明本文研究的自聚焦算法对多散射点的适应性,选取散射点模型中处于同一距离单元的散射点1和散射点2(如图2所示),在成像仿真时,在[-π,π]之间加入随机分布的相位误差如图5所示。然后分别利用PGA算法和本文算法对该距离单元进行自聚焦并完成方位压缩。图6给出了利用本文算法自聚焦并完成方位压缩后的结果,验证了本文算法对多散射点的适应性。图7为散射点1利用PGA算法和本文算法自聚焦后的方位压缩结果,从图中可以明显看出,本文算法的聚焦性能优于常用的PGA算法。
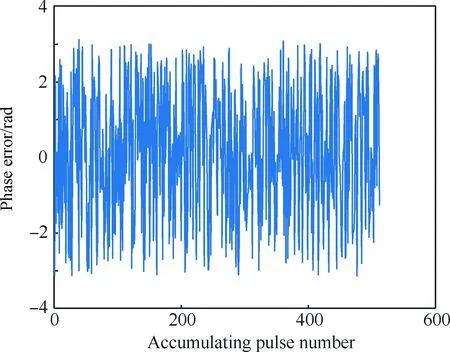
图5 相位误差序列Fig.5 Phase error sequence
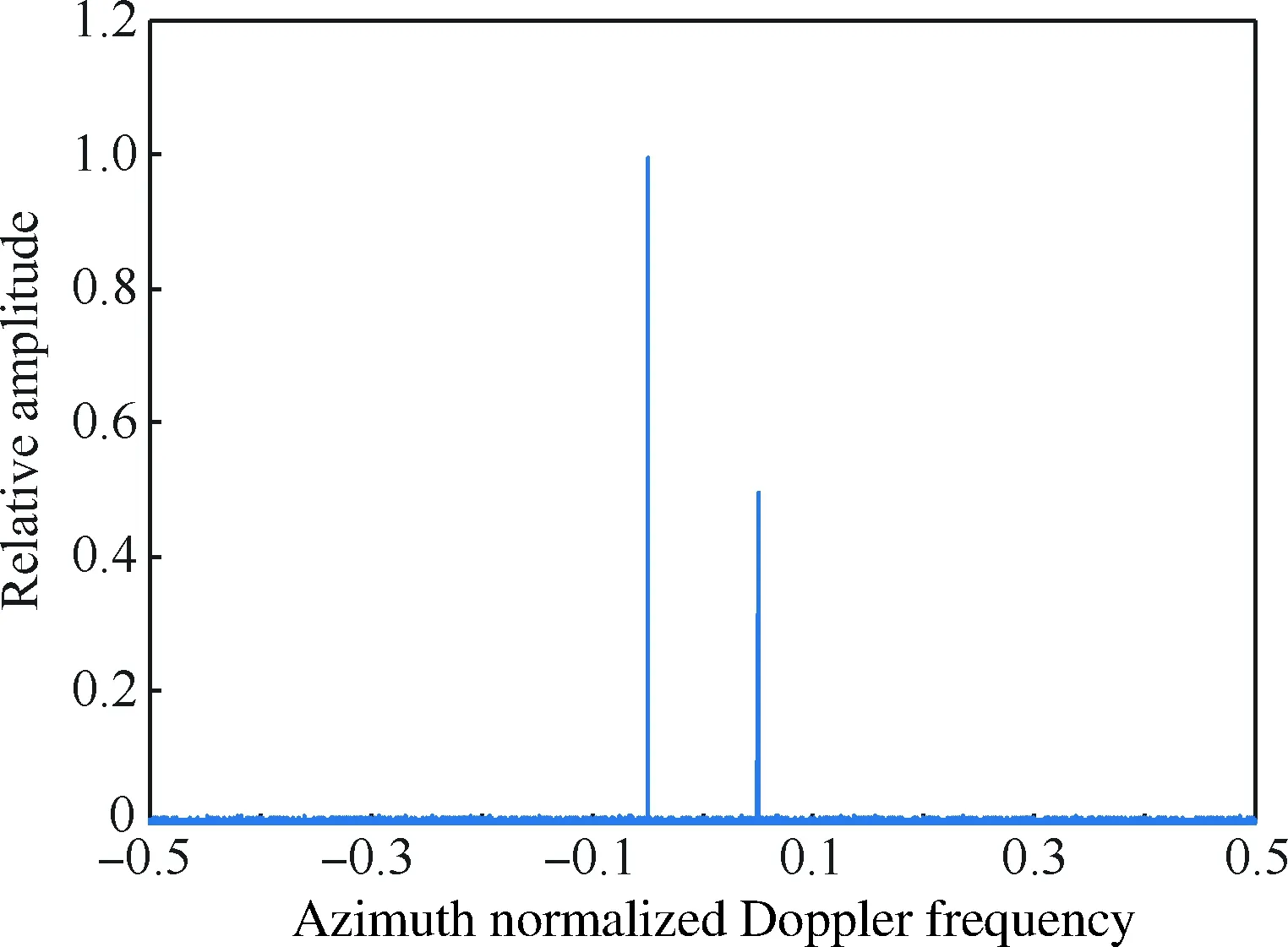
图6 本文算法自聚焦后的方位压缩结果Fig.6 Results of azimuth compression after autofocusing with proposed algorithm
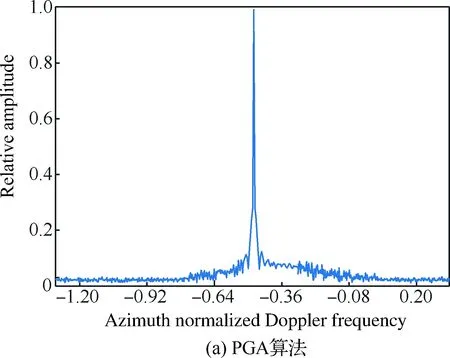

图7 两种算法自聚焦后的方位压缩结果(散射点1)Fig.7 Results of azimuth compression after autofocusing with two algorithms (Scattering point 1)
5 结 论
1) 通过选取合适的冗余字典来表示包络对齐后的一维距离像,并利用稀疏分解算法估计出二次项的系数,然后据此系数构建补偿相位项可完成图像的高精度自聚焦,与PGA算法相比,使用本文算法可得到更高聚焦精度的二维ISAR图像。
2) 算法的成功实现依赖于正则化参数的正确选择以及迭代误差门限的恰当选取,当正则化参数选取不正确时,得不到正确的稀疏分解结果,最终造成无法完成图像的自聚焦,而且当目标为具有成片连续散射面的复杂目标时,因其不满足理想散射点模型的假设,故本文算法也不适用于该类目标。
3) 研究快速恰当的参数选取方法及针对复杂目标的扩展性算法也是课题组下一步的重点研究方向。
