一类具强内射的正则环
2022-06-13刘云萍金海兰
刘云萍, 金海兰
(延边大学 理学院, 吉林 延吉 133002)
1974年, Yue C M在文献[1]中首次提出了P-内射模的概念,并利用P-内射模研究了正则环.此后,一些学者又研究了其他一些特殊内射环的正则性[2-4].2002年, Hong C Y等研究了右CP-内射环与正则环之间的关系[5].基于文献[5]的研究,本文将强CP-内射环与正则环相结合来研究强CP-内射环与正则环的等价条件.
本文中的环均指有单位元的结合环,环上的模均指酉模.设R为环,M为左R-模,如果R的任意一个主左理想I到M的左R-模同态都可以扩充到R到M的左R-模同态,则称M为左主内射模,简记为左P-内射模[1].如果左R-模RR是P-内射模,则称环R是左P-内射环.如果环R的每个环同态像都是左P-内射的,则称R为完全左主内射环,简记为左CP-内射环[6].左CP-内射环一定是左P-内射环,反之未必.
1 强正则环与弱正则环
设R为环,如果对∀x∈R, 存在y∈R, 使得xyx=x, 则称R为Von Neumann正则环.文献[1]的作者证明了环R是Von Neumann正则环当且仅当每个左R-模是P-内射模,同时还证明了环R是Von Neumann正则环当且仅当每个循环左R-模是P-内射模.由此可知Von Neumann正则环一定是左P-内射环,但反之未必.设R为环,如果对∀a∈R, 存在b∈R使得a2b=a, 则称R为强正则环.显然,强正则环一定是正则环,但反之未必.设R为环,如果对∀a∈R, 都有aR=aRaR, 则称R为右弱正则环.类似的,如果对∀a∈R, 都有Ra=RaRa, 则称环R为左弱正则环.若环R既是左弱正则环,又是右弱正则环,则称R为弱正则环.
引理1[7]环R是强正则环当且仅当R是阿贝尔正则环.
引理2①正则环一定是弱正则环; ②右弱正则环或左弱正则环一定是半素环.
证明令R是正则环,则对∀a∈R, 存在b∈R使得a=aba∈aRa.由此知aR=aRaR,Ra=RaRa, 因此R是弱正则环.引理2中的①得证.
令R是一个右弱正则环,并设对∀a∈R,aRa=0.由于R是右弱正则环,因此有aR=aRaR=0,a=0, 由此知R是半素环.同理,当R为左弱正则环时,R也一定是半素环.引理2中的②得证.
如果环R的每个极大左理想都是R的双边理想,则称R为左拟-duo环.如果环R的每个极大本质左理想都是R的双边理想,则称R为MELT环.显然,左拟-duo环一定是MELT环,但MELT环不一定是左拟-duo环.
定理1令R是MELT环,则以下条件等价: ①R是正则环; ②R是左弱正则环; ③R是右弱正则环; ④R是弱正则环.
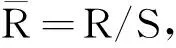
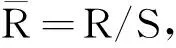
由于正则环一定是弱正则环,显然由条件①可推出条件④.由于弱正则环既是左弱正则又是右弱正则,所以由条件④可推出条件②和③.
2 强CP-内射环与正则环
如果环R的每个环同态像为左(右)R-模时是P-内射模,则称环R为强左(右)CP-内射环.由文献[1]中的证明(若R是正则环,则每个左(右)R-模都是P-内射模)知R是强左(右)CP-内射环.
引理3[8]环R是左P-内射环当且仅当R的每个主右理想是右零化子.
定理2正则环一定是左P-内射环.
证明令R是正则环,则对∀a∈R, 一定存在b∈R使得a=aba, 由此知ba是R中的幂等元.设ba=e, 则aR=eR, 于是得aR是1-e的右零化子.由引理3知,R是左P-内射环,但左P-内射环不一定是正则环.
引理4[5]令R是MELT环,则以下条件等价: ①R是正则环; ②R是强左CP-内射环.
对于环R,P(R)表示R的素根集,N(R)表示由所有幂零元构成的集合.显然P(R)⊆N(R).若P(R)=N(R), 则称R为2-primal环.若R是约化环,则根据约化环的概念可得P(R)=N(R)=0, 由此知约化环一定是2-primal环.
引理5[5]令R是一个2-primal环,则以下命题等价: ①R是强正则环; ②R是强左CP-内射环.
如果环R的每个非零左(右)理想都包含一个R的双边理想,则称R为强左(右)有界环.
引理6[5]以下命题等价: ①环R是强正则环; ②环R是强左有界环和强左CP-内射环; ③环R是强右有界环和强左CP-内射环.
定理3对于约化环R, 以下条件等价: ①R是正则环; ②R是强左有界环和强左CP-内射环; ③R是强右有界环和强左CP-内射环; ④R是强左CP-内射环.
证明由于约化环一定是阿贝尔环,所以约化的正则环一定是强正则环,故由条件①可推出条件②和条件③.
② ⟹ ①.首先利用反证法证明R/rZ(R)是一个约化环,其中rZ(R)表示R的左奇异理想.如果R/rZ(R)不是一个约化环,则存在a2∈rZ(R)使得a∉rZ(R).因此必存在环R的理想K使得l(a)⊕K∈l(a2)是左本质的.由于R是强左有界的,则必存在R的一个双边理想I使得I⊆K.由此可知Ia2=0,Ia⊆l(a)∩I⊆l(a)∩K=0, 所以有I⊆l(a),I=0, 这与I≠0矛盾.所以R/rZ(R)是一个约化环,即R/rZ(R)是一个强正则环.由此可知,R是一个左P-内射环,于是有rZ(R)=J(R), 故R是一个左拟-duo环,即R是一个强正则环.
③ ⟹ ①.首先利用反证法证明R是一个约化环.如果R不是一个约化环,设a2=0, 但a≠0, 则r(l(a))是R的一个非零右理想.由此知必存在一个R的非零双边理想I使得I⊆r(l(a)), 所以有l(a)⊆l(I), 故R/l(a)是一个左P-内射R-模.令f:Ra→R/l(I),f满足f(ra)=r+l(I), 则f是一个左R-同态映射.因为R/l(a)是左P-内射模,所以存在c∈R使得1+l(I)=f(a)=ca+l(I), 由此得1-ca∈l(I), 1∈l(I), 这与I≠0矛盾.所以R是一个约化环,即R是一个强正则环.
因约化环也是2-primal环,所以由引理5知条件①与条件④等价.
令R为环,若R的所有极大理想的交J(R)=0, 则称R为半单环[9].文献[10]的作者证明了一个半单的单边拟-duo环一定是约化环.
定理4令R是半单左拟-duo环,则以下条件等价: ①R是正则环; ②R是强左有界环且是强左CP-内射环; ③R是强右有界环且是强左CP-内射环; ④R是强左CP-内射环; ⑤R是弱左正则环; ⑥R是弱右正则环; ⑦R是弱正则环.
证明由于一个半单的单边拟-duo环一定是约化环,因此根据定理3知,定理4中的条件①—④等价.由于左拟-duo环是MELT环,进而根据定理1可以证得定理4中的条件①、⑤、⑥、⑦等价.
