低雷诺数多螺旋桨/机翼耦合气动设计

2018-08-29王科雷周洲祝小平许晓平

航空学报 2018年8期

王科雷，周洲,*，祝小平，许晓平

1. 西北工业大学航空学院，西安 710072 2. 西北工业大学无人机特种技术重点实验室，西安 710065

作为航空科学技术与新能源技术的有机结合体，太阳能无人机“采能-充能-放能”系统可以将太阳能转化为电能以驱动螺旋桨产生飞行动力，理论上具有在高空或者高高空实现真正意义上“永久”飞行的能力[1]。临近空间因其独特的资源优势与战略价值也已经发展成为世界各国航空工程研究的热点区域[2-3]。该区域内风场变化平稳，且还具有较高的太阳能利用效率，这些特点均为太阳能无人机的发展和使用提供了极优的天然环境。在先进技术推动以及强大需求牵引的共同作用下，临近空间太阳能无人机展现出极为广阔的民用及军用前景，已经成为当今航空航天大国竞相追逐的研究热点。

临近空间太阳能无人机飞行速度及所处大气环境密度均较低，其气动效率及推进效率亦较低，因而目前大多数临近空间太阳能无人机均具有显著的大展弦比机翼特征、多螺旋桨驱动特征、大柔性超轻结构特征以及高空低雷诺数特征。而从气动设计的角度讲，上述特征均将使得临近空间太阳能无人机气动设计问题变得复杂且困难，因此长期以来均侧重于低雷诺数翼型设计研究[4-7]或三维机翼设计研究[8-9]，通过对翼型或机翼气动性能的改善来提高飞行器整体气动性能。然而，此类设计并未在设计过程中引入对螺旋桨滑流影响的考虑，而对于如“Helios”太阳能无人机这种具有显著多螺旋桨驱动特征的特殊飞行器而言，其在真实飞行状态下将有较大范围的机翼是处于螺旋桨滑流影响中，此时采用常规设计方法仅对低雷诺数翼型或三维机翼进行优化设计虽然也能够带给全机一定的气动性能改善，但并未对螺旋桨滑流可能造成的不利影响进行抑制或消除，进而无法获得全机最优气动性能。因此，很有必要结合多螺旋桨/机翼这一特殊对象开展耦合气动设计研究。

自1986年Kroo[10]首次提出“在螺旋桨旋转的真实状态下进行机翼设计相比于不考虑螺旋桨滑流影响下的干净机翼设计更具意义”以来，国内外众多学者均针对考虑螺旋桨滑流影响的机翼设计问题进行了大量研究。目前，针对常规高雷诺数螺旋桨飞行器设计问题的研究文献较多，其中Veldhuis和Heyma[11]对耦合螺旋桨滑流影响下的机翼扭转角分布进行了设计研究，Rakshith等[12]对耦合螺旋桨滑流影响下的机翼弦长分布进行了设计研究，徐家宽等[13]则对耦合螺旋桨滑流影响下的气动扭转分布进行了设计研究，且都取得了不错的减阻效果。而针对低雷诺数螺旋桨飞行器设计问题的研究文献则相对较少，仅王科雷等[14]对耦合低雷诺数螺旋桨滑流影响下的机翼平面形状进行了设计研究。

尽管上述研究已经为螺旋桨飞行器气动设计问题提供了一些切实有效的设计手段，但当在工程实际中因结合太阳能无人机具体对象而引入诸如太阳能光伏组件铺设面积约束、铺设条件约束等限制条件时，可能会使得上述方法难以有效实施。另一方面，上述研究始终是将螺旋桨仅仅作为动力部件进行考虑，而非对螺旋桨/机翼整体进行耦合设计，这将难以实现对临近空间多桨布局太阳能无人机气动效能最深层次的挖掘。对于多螺旋桨/机翼这一类对象而言，影响其整体气动性能的参数众多，且各参数之间亦存在一定的弱/强耦合关系，这些都使得多螺旋桨/机翼耦合设计因计算难度大、设计复杂程度高而难以开展。

2014年美国国家航空航天局(NASA)重新调整航空研究战略，将前缘异步螺旋桨技术(Leading Edge Asynchronous Propellers Technology, LEAPTech)作为其首批航空概念计划之一进行发展。其主要原理是通过机翼前缘密集分布的螺旋桨的转动加快机翼表面空气流速，使得飞机在低速飞行状态下仍能够获得更优的升阻特性、更轻的结构重量、更高的安全性和经济性等，此外，在飞行过程中还可以依据不同的任务段特征选择性地通过控制各个螺旋桨转速或打开/关闭个别螺旋桨来调整机翼上的载荷分布形态。可以预见，这种将分布式电推进螺旋桨系统同时作为动力源与控制源的思路可以为航空领域气动设计发展带来创造性转折，同时还可以为临近空间太阳能无人机气动效率及推进效率低、大柔性轻质结构变形控制问题及振荡抑制问题等提供解决方案。

鉴于此，本文针对临近空间多桨布局太阳能无人机气动设计问题，结合LEAPTech技术思想及基本原理，将多螺旋桨驱动系统作为设计对象的一部分进行考虑，由基本流动特性及流动机理出发，进行了低雷诺数条件下的多螺旋桨/机翼耦合设计研究。研究过程中首先基于计算流体力学(CFD)方法，使用商业软件FLUENT，针对典型临近空间太阳能无人机的多螺旋桨/机翼翼段在高空低雷诺数状态下的流动特性及流场结构进行深入研究，以多螺旋桨滑流影响下的机翼近壁面流动特性及流场结构为纽带，提炼出以构造高空低雷诺数条件下多螺旋桨/机翼近壁面流态分布为核心的多螺旋桨/机翼耦合设计思想。之后，基于该设计思想进行高空低雷诺数条件下的多螺旋桨/机翼耦合设计方法的算例研究。最后，为了验证所提出低雷诺数多螺旋桨/机翼耦合设计思想及设计方法的有效性及可靠性，对多螺旋桨/机翼耦合设计得到的结果与常规仅进行低雷诺数翼型设计得到的结果进行对比分析，结果表明：与常规基于低雷诺数翼型设计的多螺旋桨/机翼设计结果相比较，基于所提出的低雷诺数多螺旋桨/机翼耦合设计思想设计得到的多螺旋桨/机翼气动特性得到显著改善，其中多螺旋桨滑流影响下机翼阻力相对降低达8.8%，机翼升阻比相对增大达12.1%，同时多螺旋桨滑流为机翼气动特性带来的不利影响亦得到约64.5%的补偿和改善。

1 气动设计思想

参考“Pathfinder”系列太阳能无人机总体布局形式及相关参数，结合其多桨布局大展弦比机翼特征，构建如图1所示的的四螺旋桨/机翼翼段模型作为对象进行分析研究，其中机翼剖面采用Clark YH反弯翼型，机翼弦长c=2.4 m，机翼展长b=20 m，机翼安装角iw=4°。螺旋桨则采用直径D=2 m的某工程用双叶螺旋桨X1，所有螺旋桨以0°安装角水平安装在机翼正前方距离机翼前缘dp-w, x=1 m的位置，各螺旋桨中心相对机翼前缘的垂向安装距离dp-w, y=0 m，相邻两螺旋桨之间距离dp-p=4 m。所有螺旋桨按右手准则沿x轴负向同步旋转。将该四螺旋桨/机翼模型的数值计算状态设定为：计算高度H=20 km，远场来流速度V∞=25 m/s，计算迎角α=0°，弦长雷诺数Rec=3.0×105，螺旋桨转速n=900 r/min。另外，考虑到本文主要关注多螺旋桨/机翼之间耦合影响，同时为了降低计算复杂程度，始终将机翼两侧平面设置为对称面以避免翼尖卷起涡的生成，从而忽略机翼三维效应影响。

由于当前计算状态下, 该四螺旋桨/机翼翼段绕流问题是处于低雷诺数范畴，在数值计算中必须考虑层流转捩的问题。因此本文主要采用基于结构-非结构混合网格技术耦合k-kL-ω转捩模型[15-16]求解雷诺平均Navier-Stokes(RANS)方程的多重参考坐标系(Multi-Reference Frame, MRF)[17-18]准定常求解方法来对多螺旋桨/机翼构型相互气动干扰问题进行数值模拟。数值计算过程中空间离散采用二阶迎风MUSCL(Monotone Upstream-centered Scheme for Conservation Laws)插值的Roe格式，时间离散与推进则采用隐式AF(Approximate Factorization)方法。其中基于局部变量“层流动能”的k-kL-ω转捩模型是基于“分裂机制”来描述层流动能的增长过程，其输运方程组可写为

图1 四螺旋桨/机翼翼段模型Fig.1 Four-propeller/wing section model

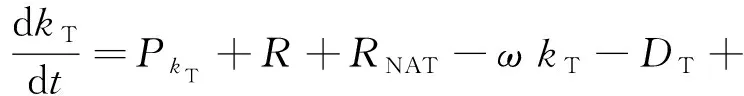
(1)

(2)

(3)

湍流动能PkT和层流动能PkL生成项及近壁面耗散项的表达式分别为

(4)

(5)

式中：x为坐标轴系，其下标i、j表示各轴系方向;k为动能;ν为黏性系数；下标T和L分别表示湍流和层流；下标s和l分别表示小尺度和大尺度；ω为湍流频率；αT为湍流标量扩散率；S为张力率梯度；R及RNAT分别为由旁路转捩和自然转捩引起的湍流产生项，其表达式分别为

R=CRβBPkLω/fW

(6)

RNAT=CR,NATβNATkLΩ

(7)

式中：Ω为涡量；fW、βBP、βNAT的表达式为

(8)

(9)

βNAT=1-

(10)

式中：Cω1、Cω2、Cω3、CωR、Cλ、CR、CR,NAT、CBP,crit、CNAT,crit、CNC和ANAT等系数的具体取值可参考文献[15]。

本节将首先对该数值模拟方法的精确性进行算例验证，从而为下文分析研究以及优化设计的可信度提供保证，然后，采用该数值模拟方法针对该四螺旋桨/机翼翼段在低雷诺数状态下的流动特性及流场结构进行分析研究，在此基础上进一步提炼出有效可行的低雷诺数多螺旋桨/机翼耦合设计思路。

1.1 数值模拟方法算例验证

为验证本文数值模拟方法中k-kL-ω转捩模型对低雷诺数转捩流动问题以及MRF对转子运动问题求解的准确性及可靠性，分别选取NLF-0416自然层流翼型算例[19]以及Caradonna-Tung旋翼算例[20]进行分析研究。

1.1.1 NLF-0416自然层流翼型算例

NLF-0416自然层流翼型扰流问题是典型的自然转捩流动算例，拥有丰富的气动力试验数据及压强测量数据。参照文献[19]中的相关试验条件及结果，选取计算状态为：计算马赫数Ma=0.1，计算迎角α=-6°～12°，弦长雷诺数Rec=2.0×106。

如图2所示，对NLF-0416自然层流翼型绕流流场采用280×130的O型计算网格进行划分，其近壁面第1层网格高度y+≈0.5。图3为不同迎角翼型计算压力系数Cp分布与试验结果对比。图4为NLF-0416自然层流翼型分别在α=0°及α=4°时的湍流动能kT分布，图中椭圆形标注为流动转捩特征位置。

由图3可以看出，本文基于k-kL-ω转捩模型的数值模拟方法在不同迎角下翼型压;力分布计

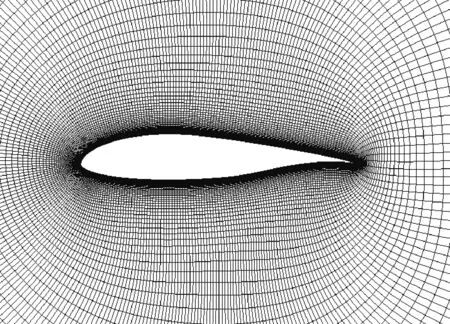
图2 NLF-0416翼型近壁面网格Fig.2 Near-wall mesh around NLF-0416 airfoil

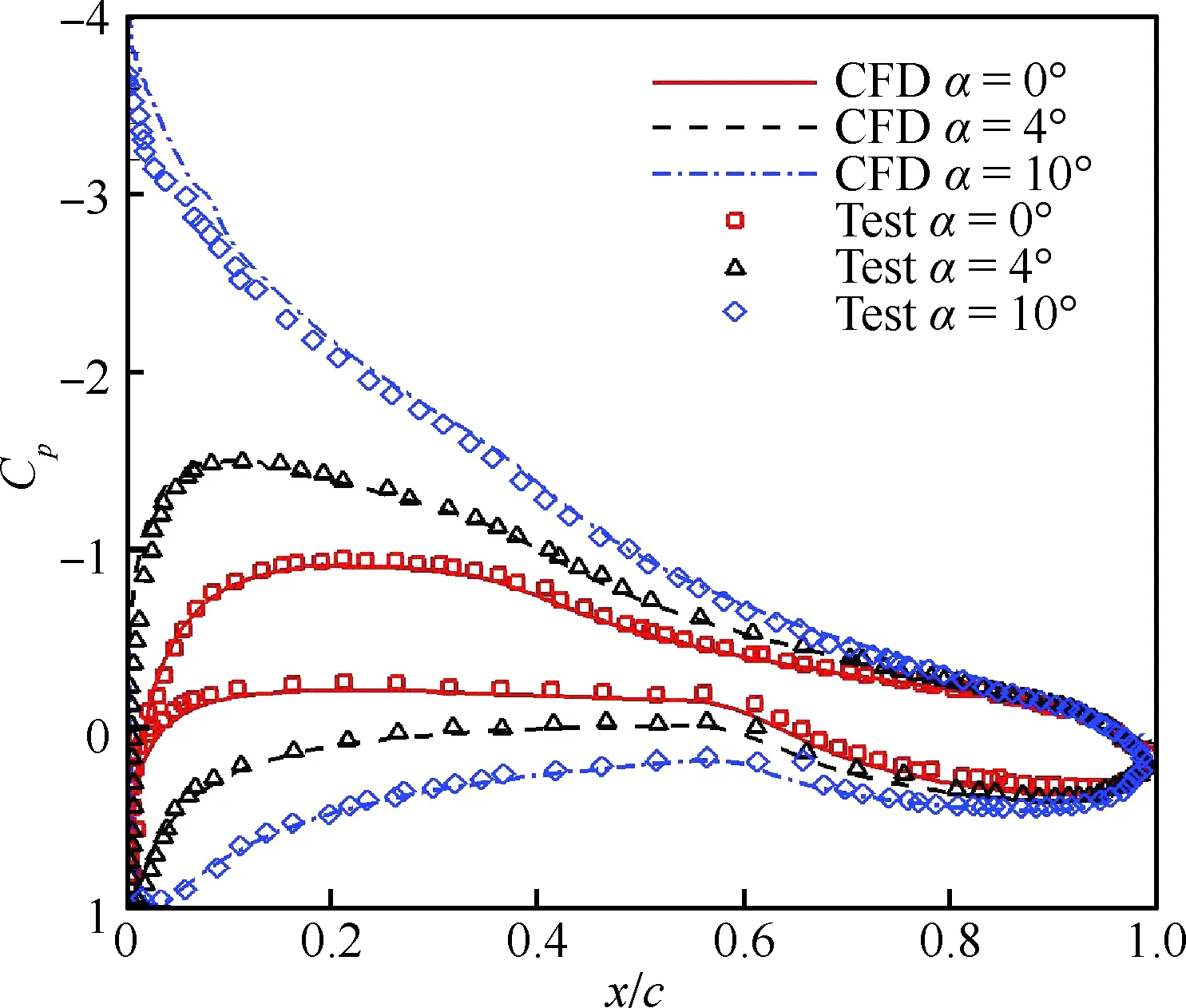
图3 NLF-0416翼型压力系数分布对比Fig.3 Comparison of NLF-0416 airfoil pressure coefficient distribution

图4 NLF-0416翼型湍动能分布Fig.4 Turbulence kinetic energy distribution around NLF-0416 airfoil

算结果与实验值吻合很好，对翼型表面压力分布特征整体预测精度高，仅在大迎角(α=10°)条件下对翼型前缘压力分布计算存在一定误差，这与试验测量误差、计算模型误差等均有关。由图4可以看出，当前计算状态下NLF-0416自然层流翼型上下表面均存在明显的流动转捩特征，而随着计算迎角的增加，翼型上表面转捩位置稍有前移，而下表面转捩位置则明显后移。

1.1.2 Caradonna-Tung旋翼算例

Caradonna-Tung旋翼绕流问题经过了大量风洞试验研究，拥有充分的测压数据，其试验结果已经被广泛地应用于旋翼绕流数值模拟方法验证计算中。参照文献[20-21]中的相关试验、计算条件及结果，选取桨距角θ=5°，转速n=650 r/min的状态进行数值计算分析。考虑数值模拟计算应与真实试验条件保持一定的相似性，将数值计算状态设置如表1所示，旋翼模型弦长为1 m，采用计算高度H=13 km时对应的环境压强及大气参数，始终保持旋翼翼尖马赫数为MaTip=0.226，以及翼尖弦长雷诺数ReTip=1.0×106。该状态下Caradonna-Tung旋翼各展向剖面翼型当地雷诺数始终处于105量级，属于低雷诺数流动范畴。

图5为采用数值模拟方法计算得到的不同径向位置(r/R)桨叶剖面翼型压力分布与试验结果之间的对比。可以看出，MRF准定常求解方法计算得到的各径向位置桨叶剖面翼型压力分布与试验结果吻合良好，其所反映出的压力分布曲线整体轮廓特征与前缘吸力峰值均与试验结果一致，数值模拟精度较高。

表1 风洞试验及数值计算状态参数对比

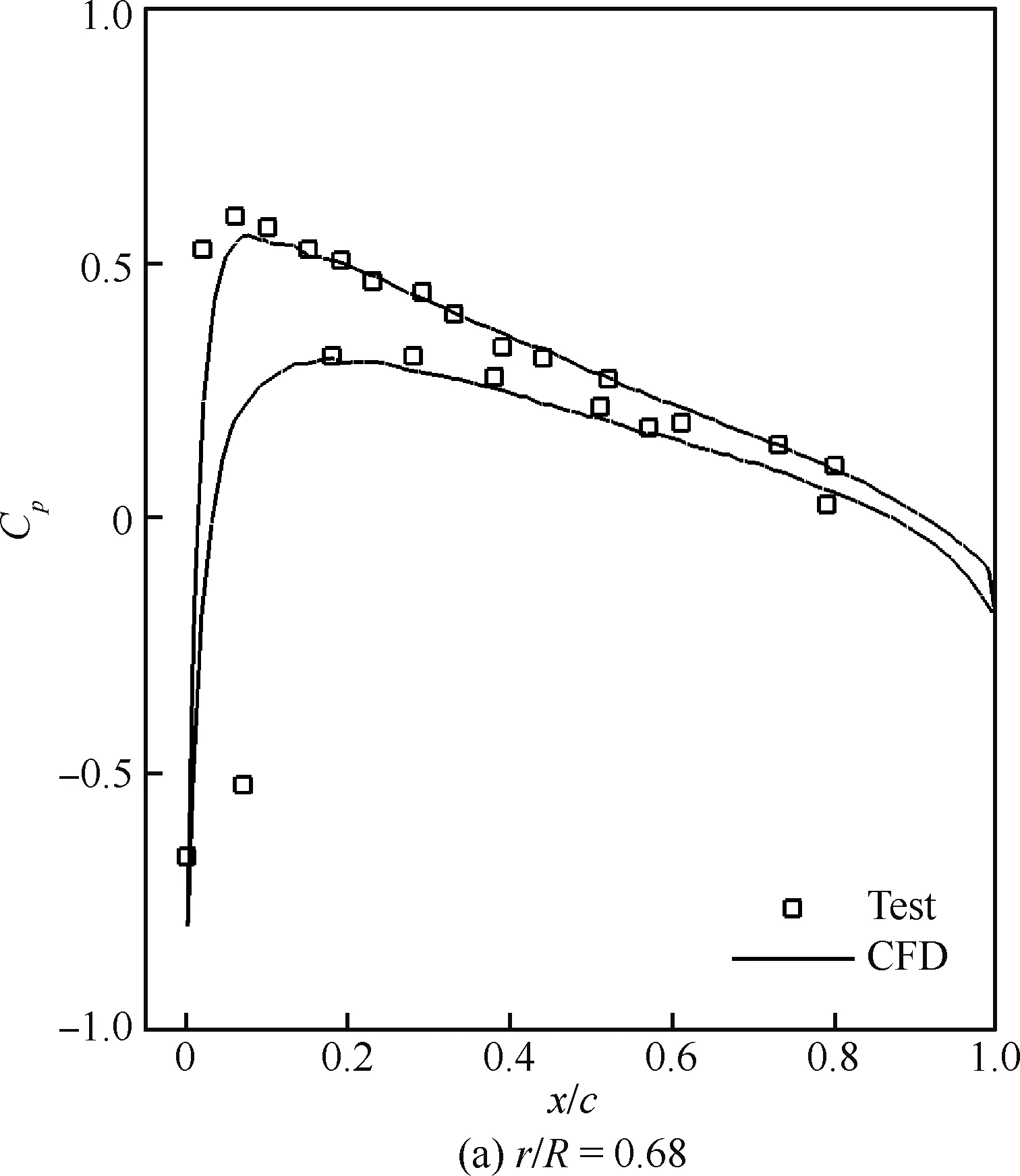
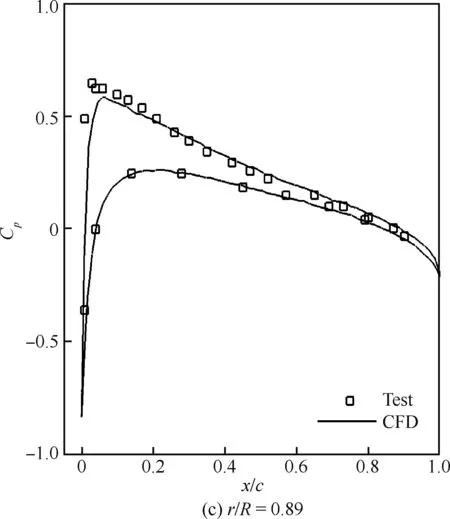
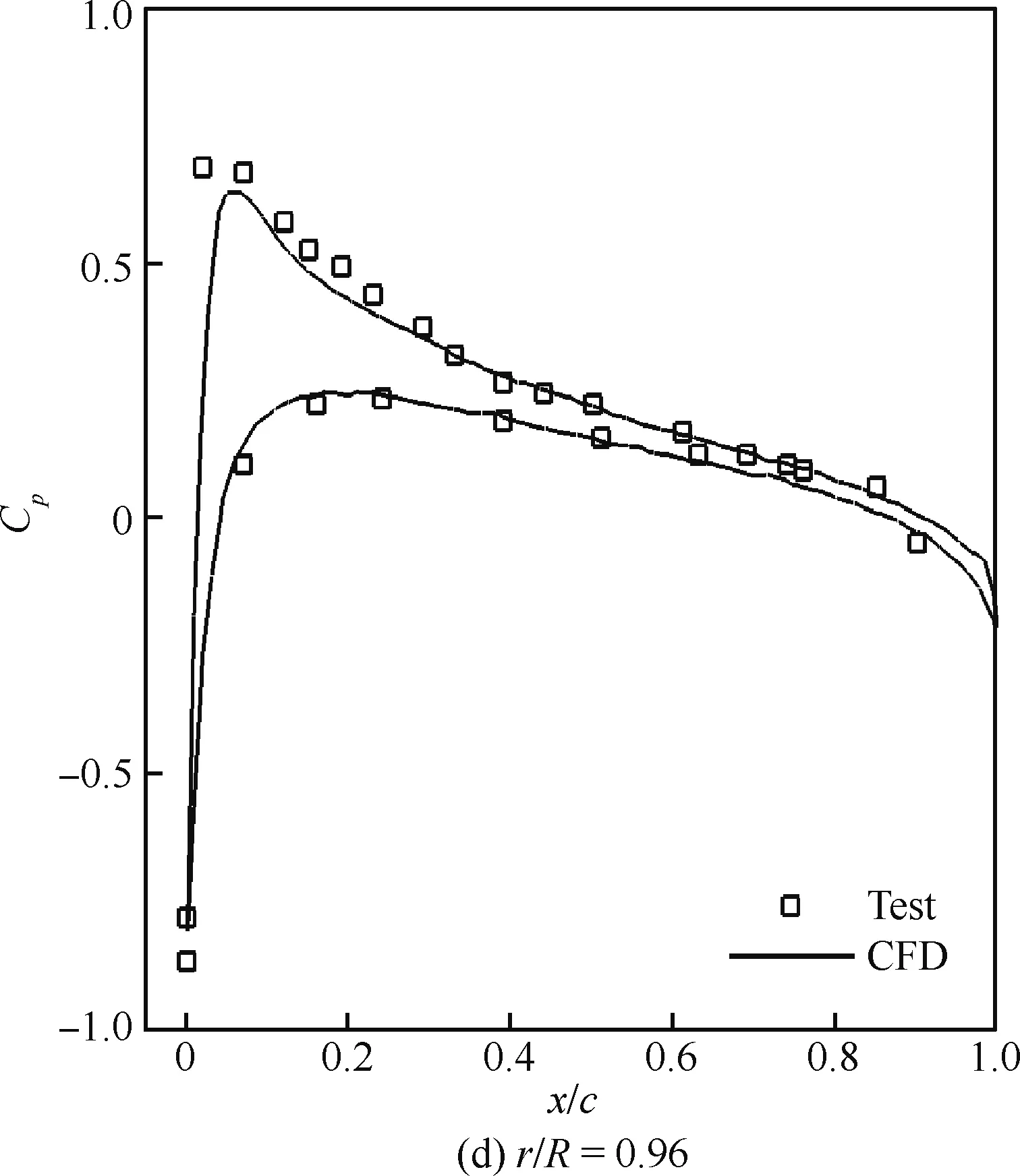
图5 旋翼剖面压力分布对比Fig.5 Comparison of pressure distribution at rotor sections

1.2 四螺旋桨/机翼气动特性及流动特性

采用上述数值模拟方法对图1所示的四螺旋桨/机翼翼段模型进行气动特性计算及分析。表2给出无螺旋桨滑流影响(Power off)及考虑螺旋桨滑流影响(Power on)两种状态下的机翼气动特性参数对比，主要包括机翼升力系数CL，阻力系数CD，压差阻力CD-P，黏性阻力CD-V，俯仰力矩系数Cm，以及升阻比CL/CD。可以看出，螺旋桨滑流影响下机翼计算升力相对稍有增大(约为0.33%)，而计算阻力则相对显著增大(约为19.90%)，这主要是由于螺旋桨滑流影响下机翼压差阻力项的显著增加(约为40.23%)，计算升阻比相对降低达16.32%。此外，机翼低头力矩相对稍有增大(约为2.24%)。

图6为采用数值模拟方法计算得到无螺旋桨滑流影响(Power off)及考虑螺旋桨滑流影响(Power on)两种状态下的机翼上表面近壁面时均流动特性分布及流场结构对比，主要包括了计算压力分布及极限流线分布，其中计算压力取为机翼表面计算结果，而极限流线则取为机翼近壁面第1层网格高度处的计算结果。

由图6可以看出：① 无螺旋桨滑流影响下机翼上表面沿展向存在平滑的低雷诺数典型层流分离泡结构(方框中)，同时其沿机翼展向分布的压强形态亦基本一致；② 考虑螺旋桨滑流影响时机翼近壁面流动状态较为复杂，其中不受螺旋桨滑流影响的机翼表面仍沿展向保持有平滑分布的层流分离泡结构，但各螺旋桨下游受滑流显著影响的机翼表面层流分离泡结构遭到严重破坏，而当前转速条件下各螺旋桨滑流显著影响区域宽度约为0.8D，D为螺旋桨直径，且总体上4个螺旋桨下游机翼近壁面流场结构之间具有一定相似性；③ 螺旋桨滑流为机翼边界层内注入能量使得其湍动能丰富程度提高，抗逆压梯度能力有所增强，但由于受到低雷诺数层流分离泡结构的耦合影响，机翼近壁面极限流线将沿展向有多次拐折而形成多个展向涡结构，此外，螺旋桨旋转效应影响下机翼前缘压力分布亦表现出上洗侧压力降低、下洗侧压力增大的特征。

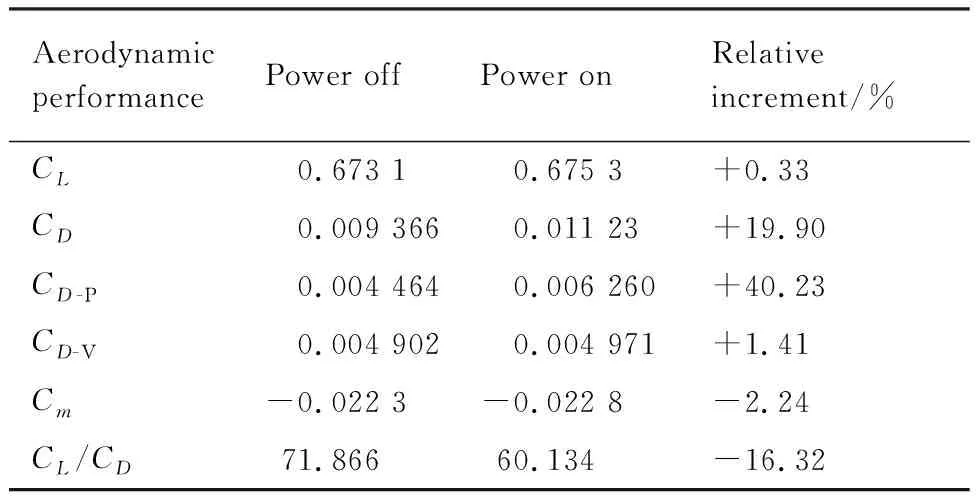
表2 机翼气动特性对比Table 2 Comparison of aerodynamic performance of wing

图6 机翼上表面时均流动特性Fig.6 Time-averaged flow characteristics on the upper surface of wing

1.3 低雷诺数多螺旋桨/机翼耦合设计思想

如图7所示，将上述多螺旋桨滑流影响下的机翼近壁面流动特性分布形式定义为3个流态区域[22]：①低雷诺数流态区域Sub-region 1，该区域内机翼近壁面流动几乎不受螺旋桨滑流影响而表现出典型低雷诺数流态特征；②近似高雷诺数流态区域Sub-region 2，该区域内机翼近壁面流动因受到螺旋桨滑流影响而将形成近似符合高雷诺数流动机理的流态特征；③速度剪切区域Sub-region 3，该区域内机翼由于受到螺旋桨滑流与低雷诺数流动中典型层流分离泡结构相互之间的耦合作用而将形成速度剪切层，进而产生较强的展向涡结构。其中当螺旋桨转速较低时，螺旋桨滑流对气流的加速效应相对旋转效应并不显著，此时螺旋桨尾流收缩现象将较为明显，Sub-region 2区域宽度将小于螺旋桨直径，而当螺旋桨转速较高时，螺旋桨滑流对气流的加速效应将更为显著，Sub-region 2区域宽度将相对有所增大。

图7 四螺旋桨滑流影响下机翼近壁面流态分布Fig.7 Flow distribution on near-wall surfaces of wing with four-propeller induced slipstream effects

显然，Sub-region 1区域流场环境与引言中所述的常规低雷诺数翼型或干净机翼的设计环境相同，基本上该区域内的翼型或机翼翼段设计均无需考虑螺旋桨滑流带来的气动影响。Sub-region 2区域流场环境则与引言中所述的常规高雷诺数条件下螺旋桨滑流影响下的流场环境相似，而相关耦合螺旋桨滑流影响的气动设计研究[10-13]，包括机翼扭转角分布设计、机翼弦长分布设计、机翼气动扭转分布设计等，也主要是对该区域内的机翼翼段三维气动特性以及表面压力分布特性进行优化设计。需要注意的是，Sub-region 3区域的存在与否即是螺旋桨/机翼相互气动干扰在低雷诺数条件与高雷诺数条件之间的主要差异，该区域内机翼近壁面流动极为复杂，由速度剪切引起的漩涡特征极为显著，这可能会造成极大的总压损失，进而造成机翼压差阻力的显著增加。因此，若要开展低雷诺数多螺旋桨/机翼耦合设计研究，在进行Sub-region 1区域以及Sub-region 2区域内的二维翼型或三维翼段气动特性的设计基础上，还需要重点针对Sub-region 3区域进行减阻设计研究。由于Sub-region 3区域内流动复杂程度高，若要像常规高雷诺数条件下直接开展耦合螺旋桨滑流的机翼气动设计，则难度将大大增加。因此，可以考虑采用降低Sub-region 3区域内速度剪切强度或减小Sub-region 3区域范围的方式来达到减阻的目的。

考虑到由于四螺旋桨/机翼构型中相邻两螺旋桨间距较大，图7中所表述的3种流态区域沿机翼展向不断重复出现，Sub-region 3区域数目及范围均较大，对应机翼阻力特性亦较差。因此，本文提出如图8所示的多螺旋桨滑流影响下的机翼近壁面理想化流态分布形式，通过有效利用各螺旋桨之间相互作用来避免速度剪切区域内强展向涡结构的产生，减小Sub-region 3区域复杂流动所带来的近壁面流动黏性耗散及总压损失，进而有效改善机翼阻力特性。

值得注意的是，理想化流态分布形式的获取需要建立在相邻两螺旋桨能够产生耦合影响的前提下，也即Sub-region 2区域宽度需要满足一定条件，这就需要对螺旋桨自身气动特性、螺旋桨转速、相邻螺旋桨相对位置关系等进行设计。

综上所述，基于系统分解的思想，建立如图9所示的设计框架来进行低雷诺数多螺旋桨/机翼耦合设计研究，图中：f(X,Y,Z)为优化函数；X、Y、Z为3组不同的设计变量；h(X,Y,Z)

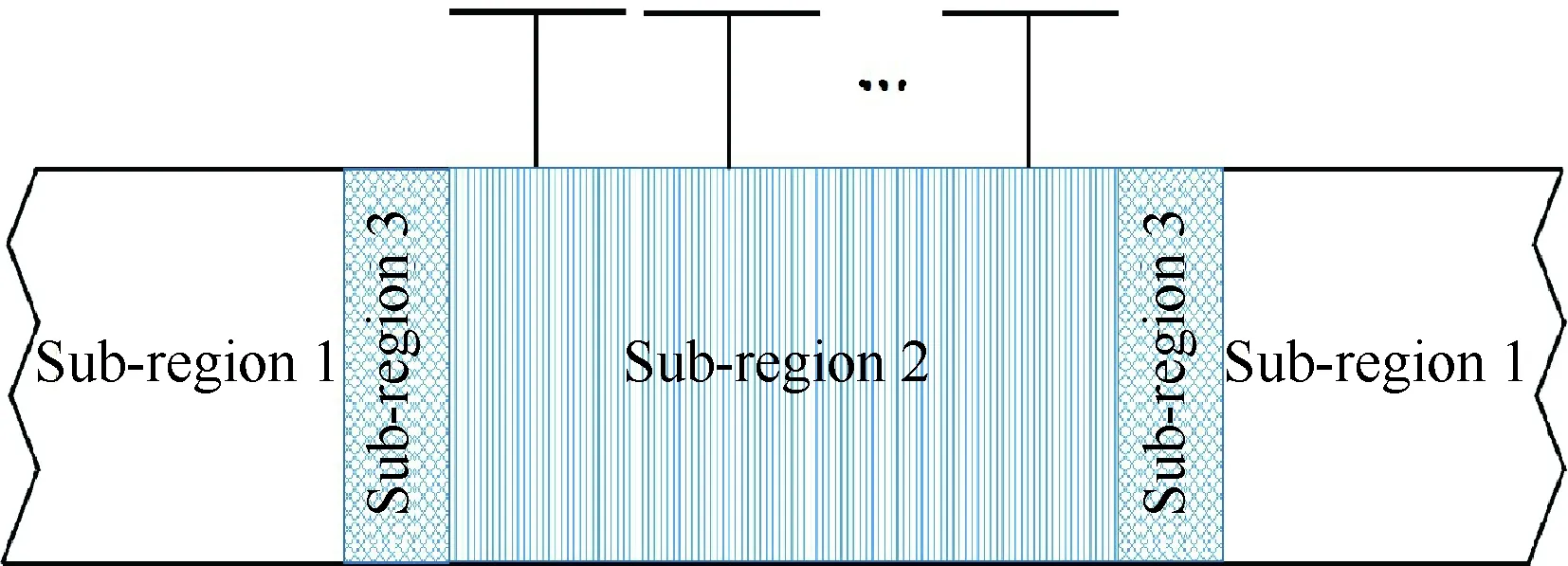
图8 多螺旋桨滑流影响下的机翼近壁面理想化流态分布Fig.8 Ideal flow distribution on near-wall surfaces of wing under multi-propeller induced slipstream effects

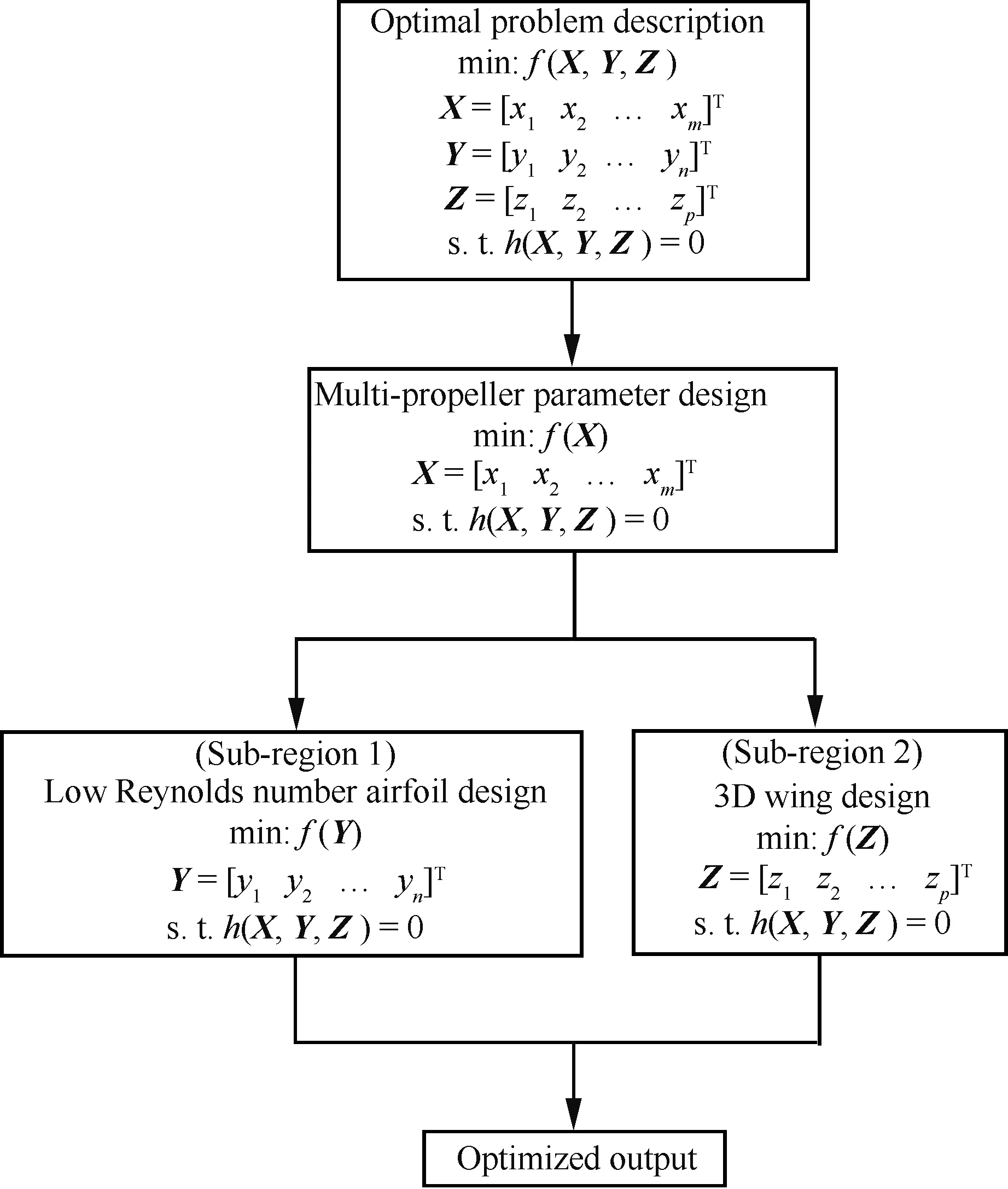
图9 低雷诺数多螺旋桨/机翼耦合优化设计框架Fig.9 Framework for multi-propeller/wing coupled optimization design at low Reynolds number

则表示约束条件函数。其核心思想是以构建多螺旋桨滑流影响下机翼近壁面理想化流态分布形式为纽带，将多螺旋桨/机翼耦合设计问题进行解耦，依次通过获得机翼近壁面理想化流态分布形式的多螺旋桨布局参数设计，低雷诺数流态区域Sub-region 1内的二维剖面翼型设计，以及近似高雷诺数流态区域Sub-region 2内的三维机翼翼段设计共3个层次设计近似实现低雷诺数条件下的多螺旋桨/机翼耦合设计目标。在设计过程中，结合某型多桨驱动太阳能无人机实际工程设计需要，始终以二维翼型及三维机翼翼段的最大厚度位置、最大厚度、机翼后缘厚度以及设计状态下纵向力矩系数保持不变为约束条件进行设计。另外，为了避免造成因减少螺旋桨滑流影响范围而带来机翼气动特性改善的误解，在进行多螺旋桨布局参数设计时始终以多螺旋桨总拉力及直径之和(近似表示滑流影响区域宽度)保持不变为约束条件进行设计。

2 气动设计方法

本节主要对图9描述的各个设计层次所采用的设计方法进行详细介绍，并结合具体算例对各设计层次设计前后所得到的不同模型的气动特性进行对比分析，以此来验证所提各设计层次设计方法的有效性及可靠性。

2.1 多螺旋桨布局参数设计

2.1.1 问题描述与方法

为获取如图8所示的多螺旋桨/机翼构型理想化流态分布形式，本节通过多螺旋桨布局参数的匹配设计来对机翼近壁面流态分布形式进行理想化重构，进而改善多螺旋桨滑流影响下的机翼升阻特性。然而，可进行设计的多螺旋桨布局参数众多，如螺旋桨数目、安装位置、转速、直径以及螺旋桨之间安装距离等，若直接对所有参数进行优化将显得不切实际。结合实际工程需求及相关设计经验设定以下约束条件：①保持设计状态下多螺旋桨提供的总拉力值Ttotal以及所有螺旋桨直径D之和始终为定值，从而在螺旋桨数目Num、转速n及直径D之间建立一定联系，达到减少设计变量个数的目的；②基于上文“各螺旋桨滑流影响下机翼近壁面流场结构具有一定相似性”的结论，将同步同向旋转的多螺旋桨整体相对机翼的安装位置设计问题转变为单独螺旋桨相对机翼的安装位置以及相邻螺旋桨之间间距设计问题，从而降低数值计算难度。本节多螺旋桨布局参数设计变量将减少为3个：螺旋桨数目Num(与螺旋桨转速n及直径D相关联)、单独螺旋桨相对机翼的流向安装位置dp-w，以及相邻螺旋桨间距dp-p。而多螺旋桨布局参数设计目标则确定为：优化构型机翼相对于基准构型机翼的升力增量ΔCL与阻力减小量ΔCD之比达到最大。该优化设计问题可以表达为

(11)

如图10所示，采用多岛遗传优化算法(Multi-Island Genetic Algorithm，MIGA)[23]为搜索器进行单目标寻优，其中子群规模设定为6，岛屿数为12，遗传代数设定为20，交叉率设定为0.7，变异率设定为0.3，岛间迁移率设定为0.5，迁移间隔代数设定为4。

具体设计步骤可以概括为：①建立满足等拉力条件及等螺旋桨直径之和条件的螺旋桨数目、转速及直径之间的关系；②逐渐增加螺旋桨数目以提高螺旋桨转速，从而为机翼近壁面理想化流场重构提供条件，判断准则为计算得到的螺旋桨滑流影响下近似高雷诺数流态区域宽度是否大于或等于螺旋桨直径，若是则进行后续螺旋桨安装位置参数设计，若否则继续增加螺旋桨数目，显然这一步需要人工介入；③对相邻螺旋桨间距dp-p以及单独螺旋桨相对机翼的流向安装位置dp-w进行最优匹配设计，并输出最终设计结果。

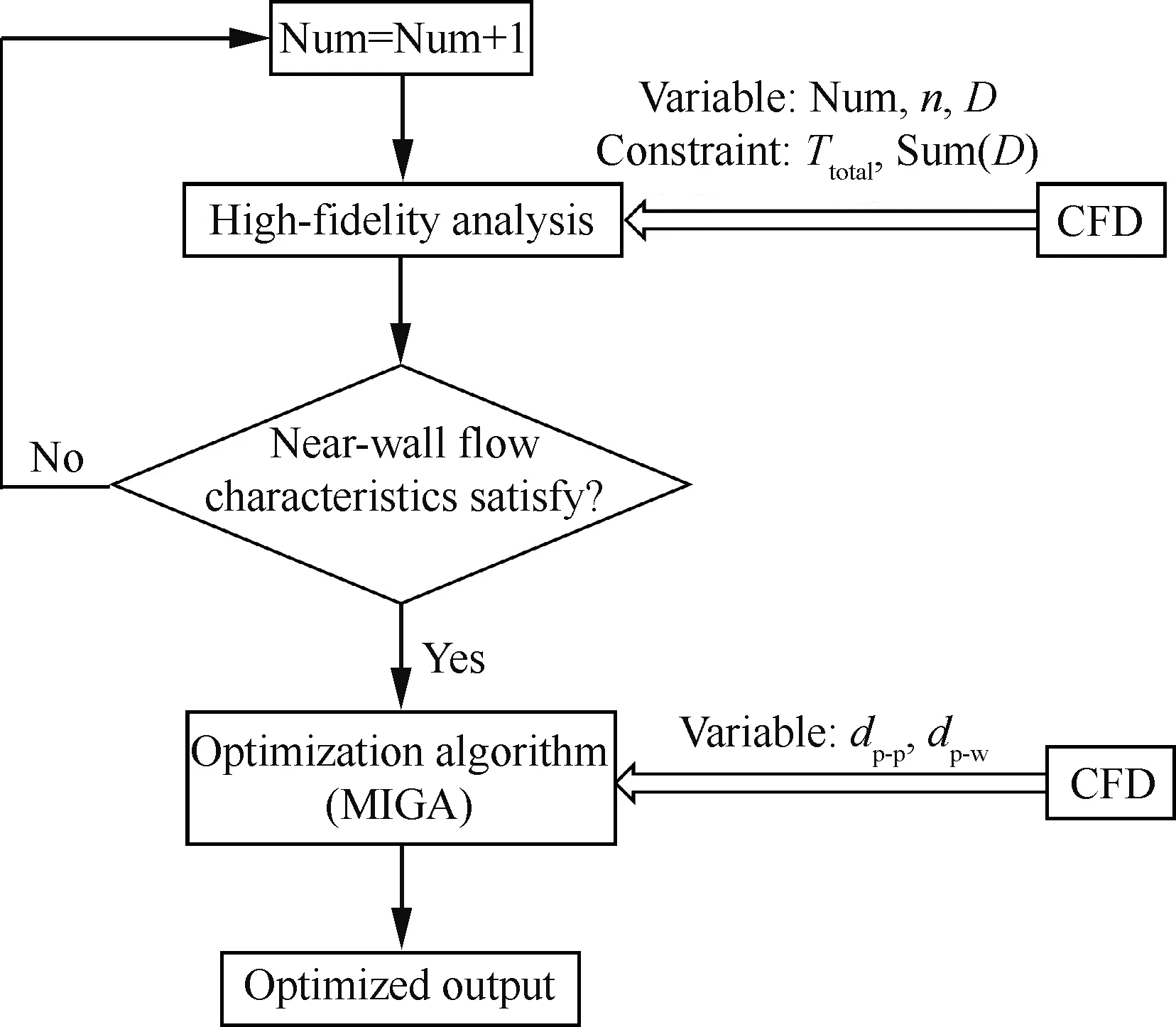
图10 多螺旋桨参数设计流程Fig.10 Multi-propeller parameter design framework

2.1.2 结果与分析

图11为多螺旋桨/机翼基准构型(Base Configuration)及优化构型(Optimal Configuration)的对比(俯视图)。其中，多螺旋桨/机翼优化构型共采用了10个直径为0.8 m的螺旋桨，各螺旋桨转速n=2 500 r/min，各螺旋桨中心距离其下游机翼前缘沿流向距离dp-w=0.6 m，相邻两螺旋桨间距dp-p=0.9 m。

表3给出设计状态下基准构型及优化构型多螺旋桨滑流影响下的机翼气动特性参数对比。可以看出，与基准构型相比较，在提供相近拉力的前提条件下，优化构型多螺旋桨滑流影响下的机翼计算升力相对有所增大(约2.44%)，计算阻力相对有所减小(约5.79%)，其中计算压差阻力相对显著降低达13.26%，计算黏性阻力则相对稍有增大(约3.62%)，机翼计算升阻比则相对增大达8.74%。最终优化构型机翼相对基准构型机翼在多螺旋桨滑流影响下的升力增量ΔCL与阻力减小量ΔCD之比达到25.39，达到设计目的。

图11 优化前后多螺旋桨/机翼构型对比Fig.11 Comparison of multi-propeller/wing configuration before and after optimization

表3 多螺旋桨/机翼构型优化前后机翼气动特性对比

Table 3 Comparison of aerodynamic performance ofwing before and after optimization of multi-propeller/wing configuration

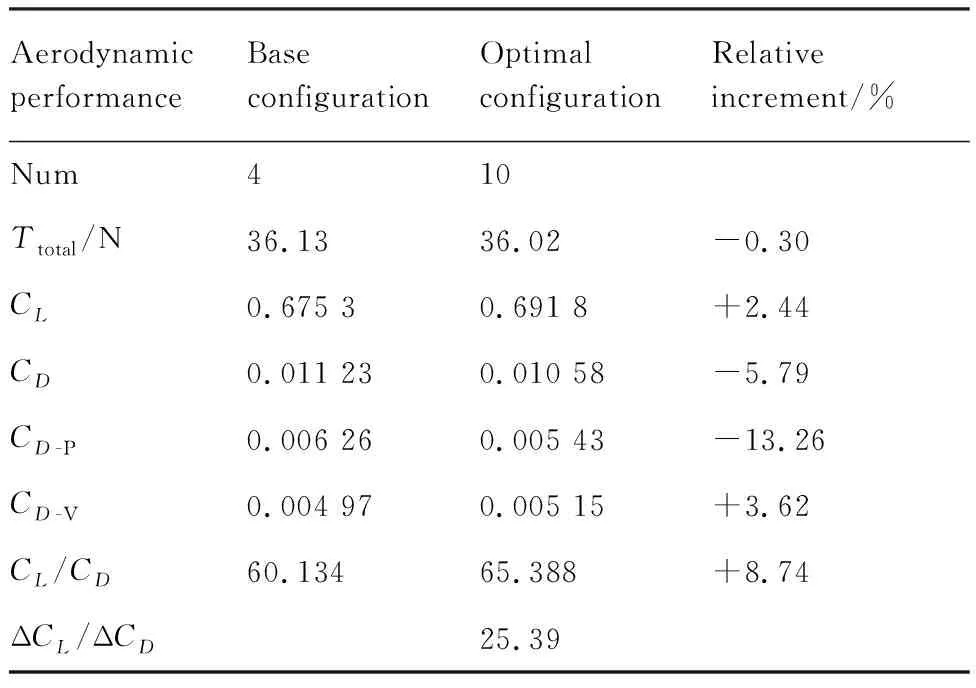
Aerodynamic performanceBase configurationOptimal configurationRelative increment/%Num410Ttotal/N36.1336.02-0.30CL0.675 30.691 8+2.44CD0.011 230.010 58-5.79CD-P0.006 260.005 43-13.26CD-V0.004 970.005 15+3.62CL/CD60.13465.388+8.74ΔCL/ΔCD25.39

图12为设计状态下不考虑螺旋桨滑流影响的干净机翼(Clean Wing)、基准构型多螺旋桨滑流影响下机翼(Base Configuration Wing)以及优化构型多螺旋桨滑流影响下机翼(Optimal Configuration Wing)之间展向升力分布曲线对比。其中机翼翼段沿展向被平均划分为20个，且各机翼翼段计算升力系数参考面积均取为机翼总面积。此外，图12中各螺旋桨均按顺时针方向旋转，也即各螺旋桨左侧为气流上洗侧，右侧为气流下洗侧。可以看出，基准构型各螺旋桨滑流诱导下机翼沿展向的升力分布曲线呈现出气流上洗侧升力显著增大，气流下洗侧升力显著减小的特征，而优化构型多螺旋桨滑流诱导下各机翼翼段计算升力均相对显著增加，且中间区域机翼翼段升力增加幅度相对基准构型各螺旋桨气流上洗侧升力增加幅度稍小但较为接近。这是因为优化构型螺旋桨转速的增大使得其滑流加速效应极为显著，占据主导地位，对应各螺旋桨下游机翼翼段因始终处于高速滑流中而产生相对显著增大的升力。

图13为优化构型多螺旋桨滑流影响下的机翼上表面时均流场特性分布示意，主要包括了计算压力分布以及极限流线分布，其中计算压力取为机翼表面计算结果，而极限流线则取为机翼近壁面第1层网格高度处的计算结果。

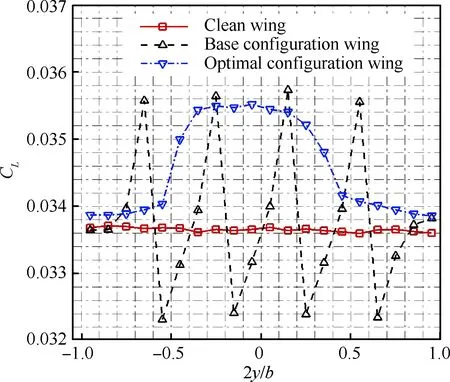
图12 机翼展向升力分布对比Fig.12 Comparison of wing span-wise lift distribution

图13 优化构型多螺旋桨滑流影响下机翼上表面时均流动特性分布Fig.13 Time-averaged flow characteristics distributed on the upper surface of wing under multi-propeller-induced slipstream effects in the optimal configuration

由图13可以看出，优化构型多螺旋桨滑流影响下机翼上表面流场结构在整体上与前文所描述的理想化流态分布形式相吻合。而由于各螺旋桨对气流的加速作用及机翼边界层内黏性耗散程度并不均匀，在相邻两螺旋桨之间的机翼近壁面流动较为复杂，主要表现为在滑流交界区域内存在有较多较弱的展向涡结构。另外，由于螺旋桨滑流在抵达机翼表面后受到黏性耗散影响，其影响区域沿流向逐渐扩大，主要表现为螺旋桨滑流诱导下机翼近壁面集中流线束逐渐散开。

2.2 低雷诺数流态区域二维翼型设计

在获取如图13所示的多螺旋桨/机翼优化构型的理想化流态分布形式之后，针对机翼两侧不受螺旋桨滑流影响的低雷诺数流态区域内的二维剖面翼型外形轮廓进行气动优化设计。

2.2.1 问题描述与方法

采用在翼型和机翼设计中应用极为广泛的Hicks-Henne型函数方法[24]对低雷诺数流态区域内二维剖面翼型进行参数化建模。Hicks-Henne型函数方法是通过在基准翼型的不同区域进行扰动函数的叠加以改变外形，翼型几何形状可以表示为

(12)

式中:yb表示基准翼型几何形状;y表示待求翼型几何形状;N为控制点个数；αi为扰动的加权系数；fi为光滑几何形线的扰动形状函数，选择扰动函数形式为

(13)

式中：xk为第k个控制点的位置。

针对低雷诺数流态区域二维剖面翼型共选取5个控制点，各控制点相对翼型弦长的位置分别为：0.1、0.2、0.4、0.6、0.9，各控制点对应扰动函数中的n均取为3。设计过程中结合实际工程中结构强度需求及载荷空间需求，将翼型最大相对厚度(t)、最大厚度位置及后缘厚度(tTE)约束保持不变，另外，将优化翼型纵向力矩参数(Cm)约束为与初始翼型纵向力矩参数相对偏差不超过10%。优化设计目标则确定为：优化翼型升力与阻力之比最大。该优化设计问题可以表达为

(14)

为了在优化过程中引入对层流分离泡进行经验性的引导和控制，建立如图14所示流程对二维剖面翼型进行优化设计。而为了进一步提高设计效率，在设计过程中采用构建Kriging代理模型[25]的方式来逼近并代替实际数值计算过程。

具体设计步骤可以概括为：①采用均匀设计方法[26]进行初始种群抽样，将初始样本点数目设定为80，基于CFD方法并行计算出各样本点翼型气动特性参数，进而建立Kriging代理模型；

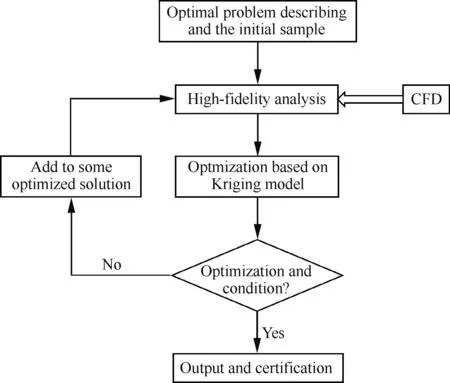
图14 低雷诺数流态区域二维翼型设计流程Fig.14 Framework for optimization design of 2D airfoil in low Reynolds number region

②基于 Kriging代理模型采用MIGA优化算法为搜索器进行单目标寻优；③判断是否满足优化终止条件，若是，则输出优化结果并进行数值验证，若否，则选取5个表现优异的优化解加入样本点集，完成Kriging代理模型更新以进一步提高模型精度，重复优化迭代直至得到可行的结果。

2.2.2 结果与分析

图15为基准翼型(Base Airfoil)及优化翼型(Optimal Airfoil)之间外形轮廓对比。可以看出，优化前后翼型最大厚度及最大厚度位置基本保持一致，但与基准翼型相比，优化翼型前缘上表面轮廓曲线趋于饱满，而前缘下表面轮廓曲线则稍显尖锐，这使得其头部附近区域相对弯度有所增大，而翼型中部区域相对弯度则有所降低，另外，优化翼型上表面压力恢复区域曲线斜率相对基准翼型亦有所增大。

图16为优化前后翼型在设计状态下的气动特性曲线对比。由图可以看出：① 全计算迎角范围内，优化翼型计算升力相对基准翼型有所增大，但升力线斜率与基准翼型基本保持一致，这主要是因为低雷诺数优化翼型头部区域相对弯度的增大致使翼型前缘吸力峰值的增加。② 设计迎角下优化翼型计算阻力系数相对基准翼型降低约24 counts，且在-2°～10°常用迎角范围内，优化翼型阻力特性相对基准翼型较优。③ 设计迎角下优化翼型俯仰力矩系数Cm与基准翼型基本保持一致，满足优化设计约束条件。但值得注意的是，低雷诺数优化翼型相对基准翼型弯度分布的显著改变使得其力矩特性亦发生显著改变，主要表现在随着迎角增大，基准翼型抬头力矩不断增大，而优化翼型力矩系数则始终稳定。这可能是因为在大迎角下基准翼型上表面层流分离泡结构前移的同时分离泡长度显著增大，翼型前缘吸力峰值及翼型后半段升力损失均不断增大，进而使得翼型整体上抬头力矩不断增大。④ 在全计算迎角范围内，优化翼型升阻比K始终相对基准翼型更大，而优化翼型最大升阻比相对基准翼型增大达11.7%。

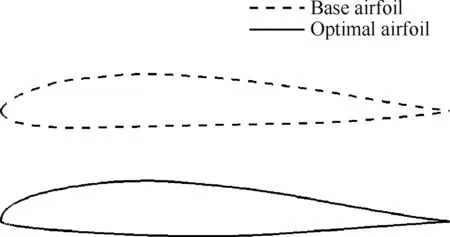
图15 优化前后翼型外形轮廓对比Fig.15 Comparison of airfoil profile before and after optimization

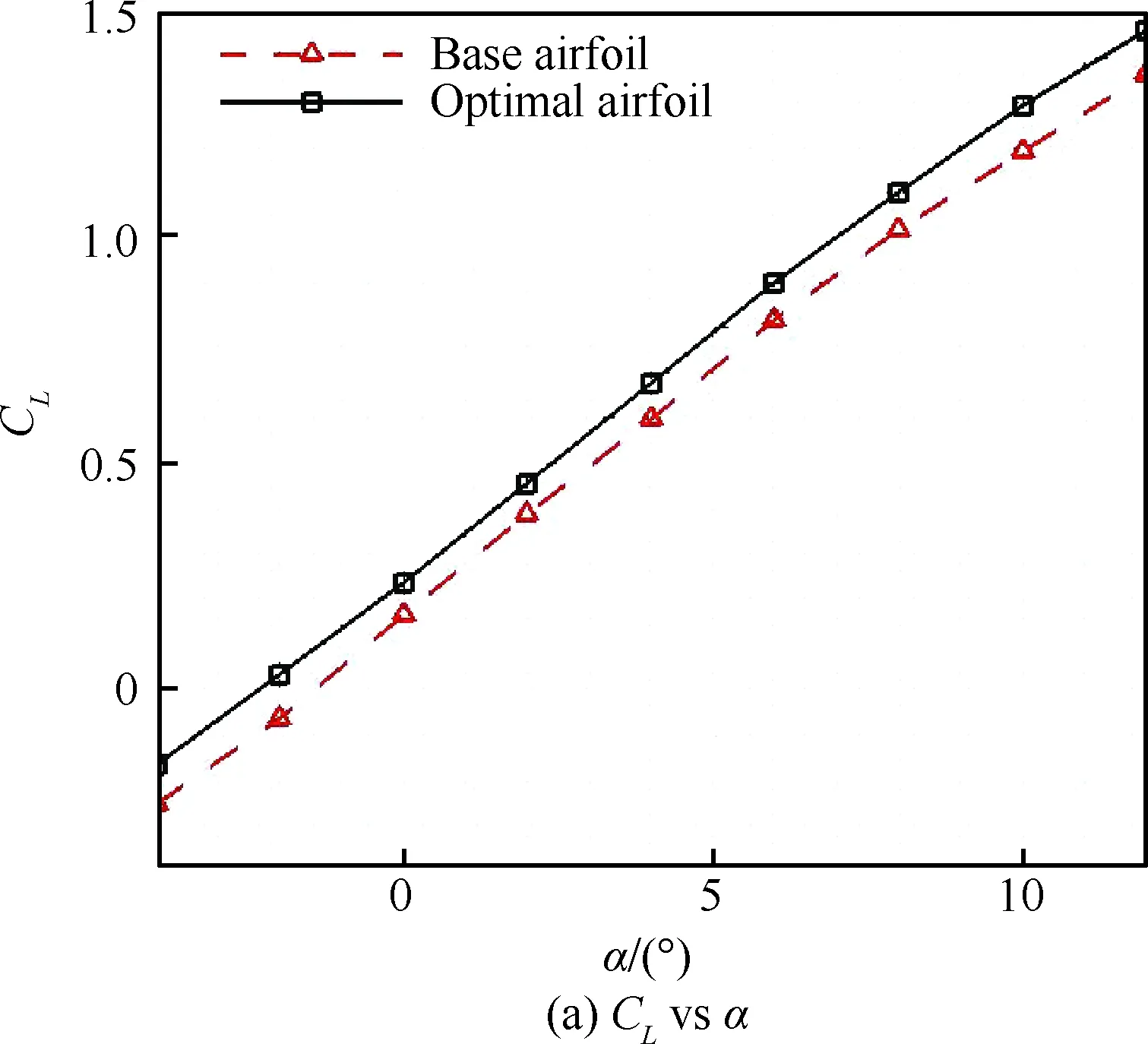
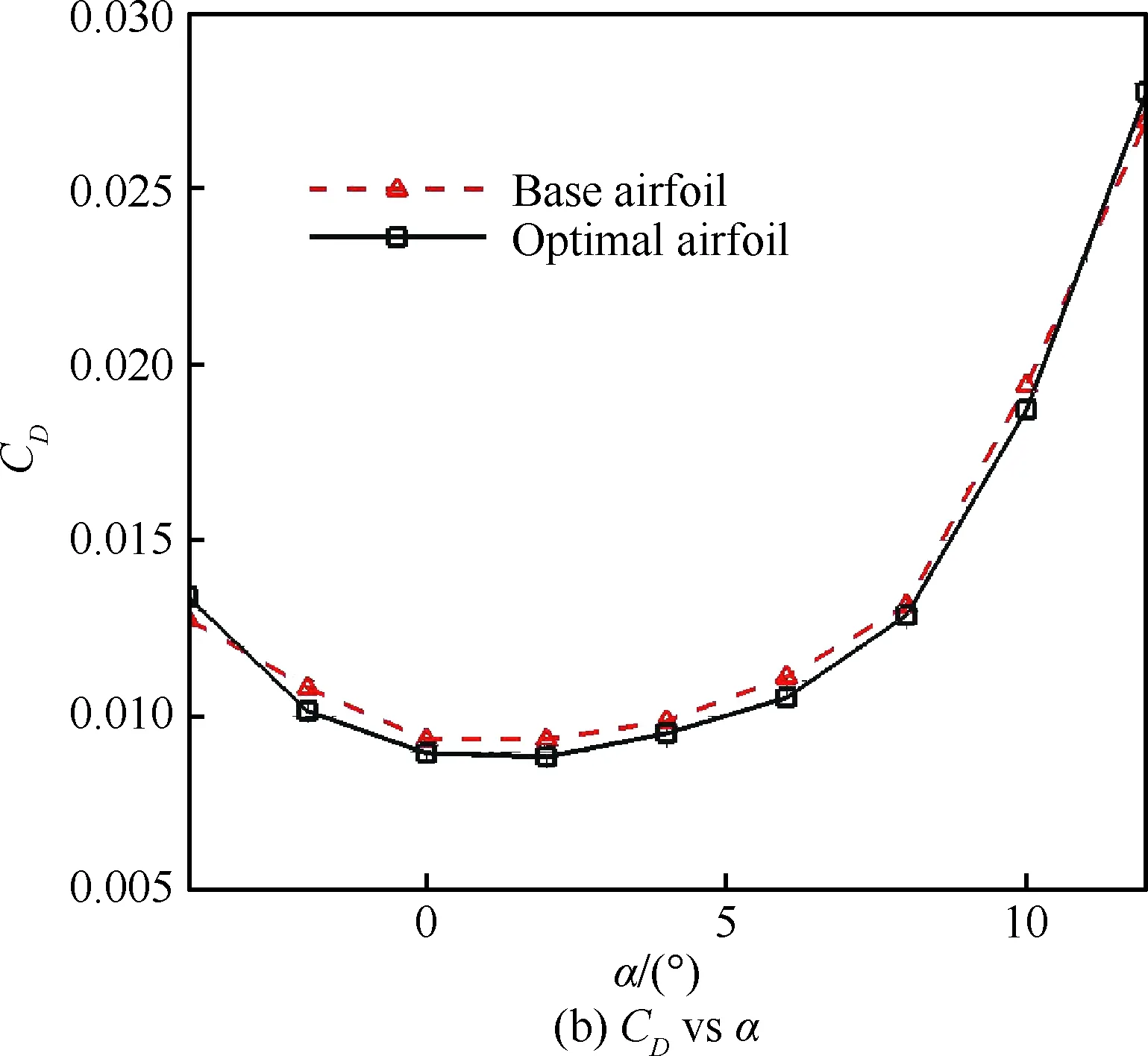
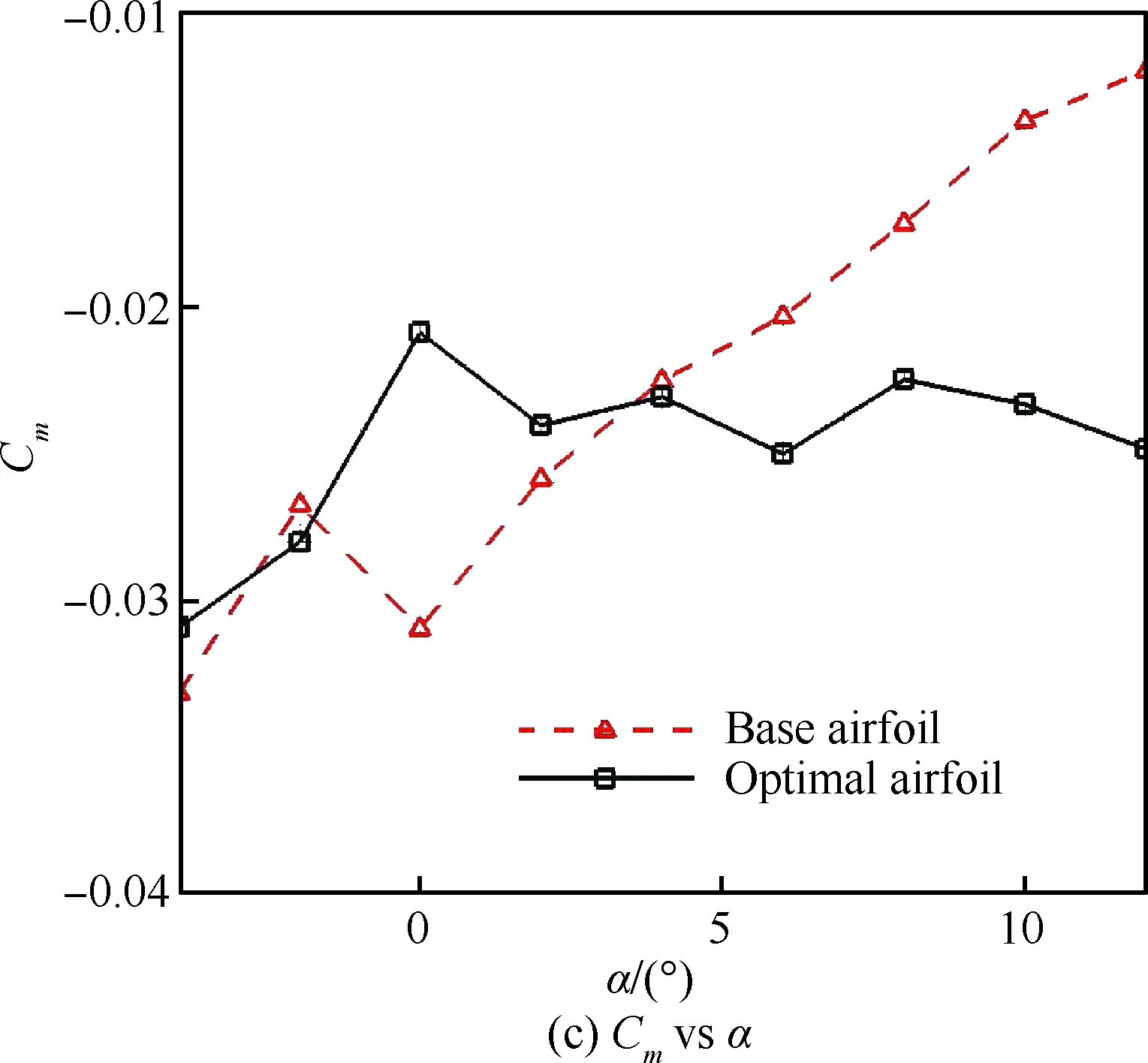
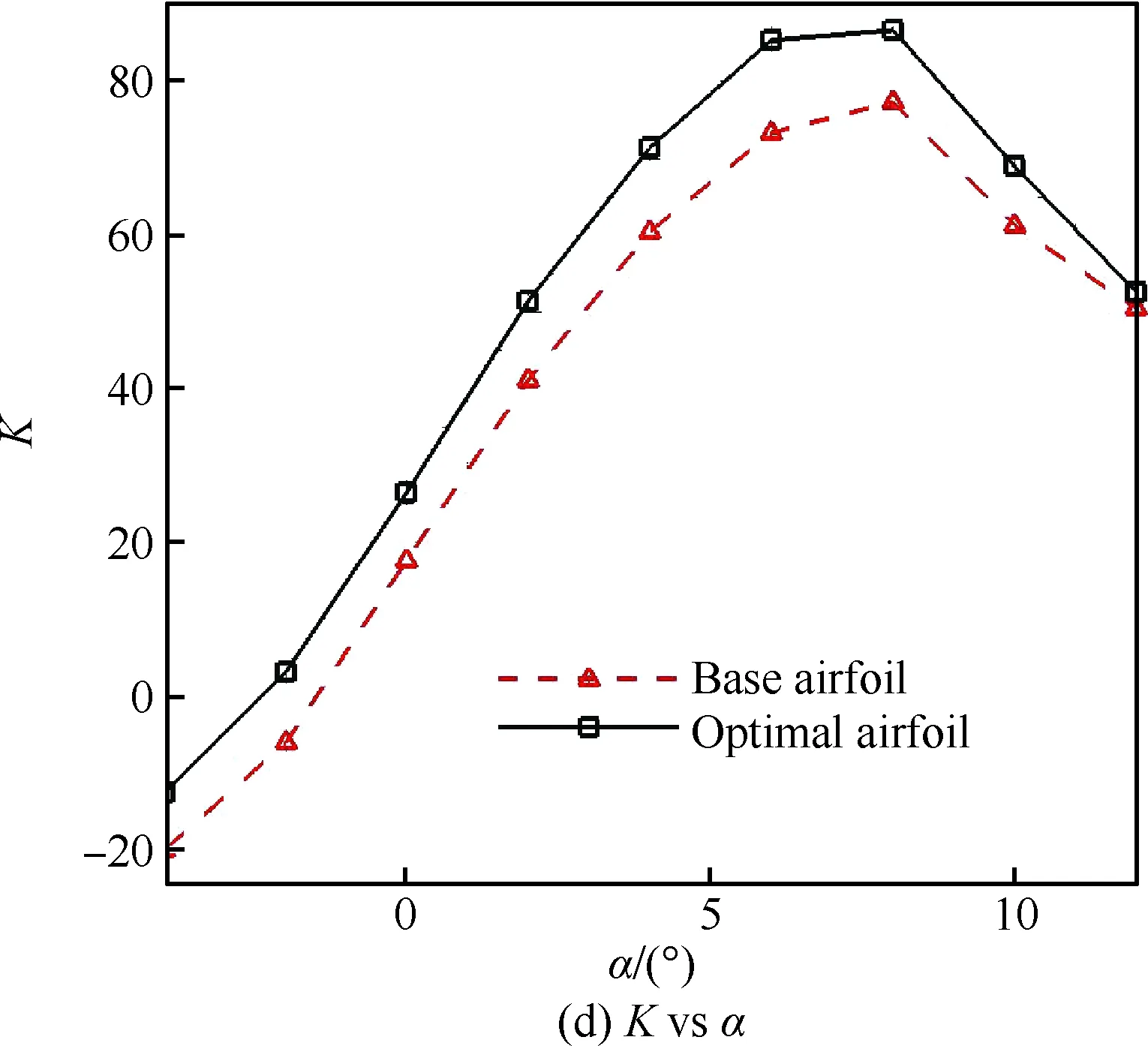
图16 优化前后翼型气动特性对比Fig.16 Comparison of airfoil aerodynamic performance before and after optimization

表4给出2°及4°计算迎角下优化前后翼型上表面边界层内流动特征位置对比，其中xS、xT、xR分别为流动分离、转捩及湍流再附发生的位置，lLSB为层流分离泡长度。

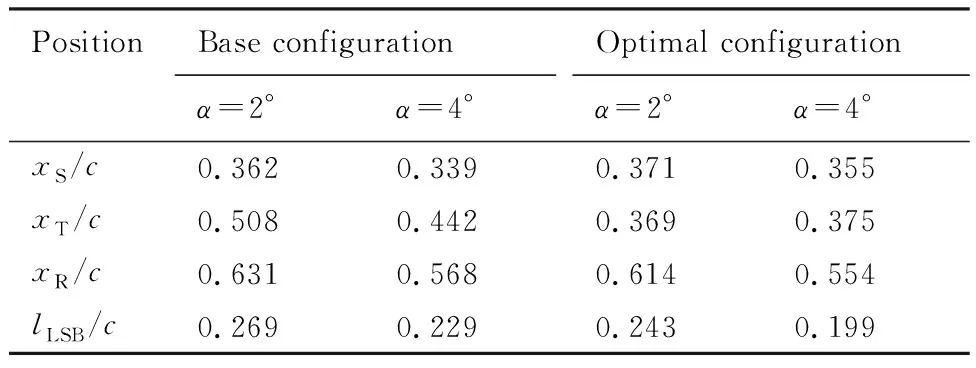
表4 翼型上表面边界层内流动特征位置对比

由表4可以看出，与基准翼型相比较，优化翼型上表面边界层内流动分离位置相对推迟，流动转捩位置相对提前，而流动再附位置则相对提前，层流分离泡结构长度相对减小。这也就是说，优化翼型上表面在具有比基准翼型更大范围层流附着流动的同时，还通过曲率控制促使流动分离后的迅速转捩，因而具有比基准翼型更短的层流分离泡结构，这也是优化翼型升阻特性相对基准翼型更优的主要原因。

2.3 近似高雷诺数流态区域机翼翼段设计

针对多螺旋桨下游直接受到滑流影响的近似高雷诺数流态区域内的机翼翼段进行气动优化设计。考虑到按照理想化流场重构思想设计得到的近似高雷诺数流态区域内各螺旋桨滑流影响下机翼翼段气动特性将极为相似，构建如图17所示的单独螺旋桨滑流影响下的机翼翼段进行优化设计，设计过程中始终将该机翼翼段两侧端面设置为对称面以规避翼尖卷起涡的影响。

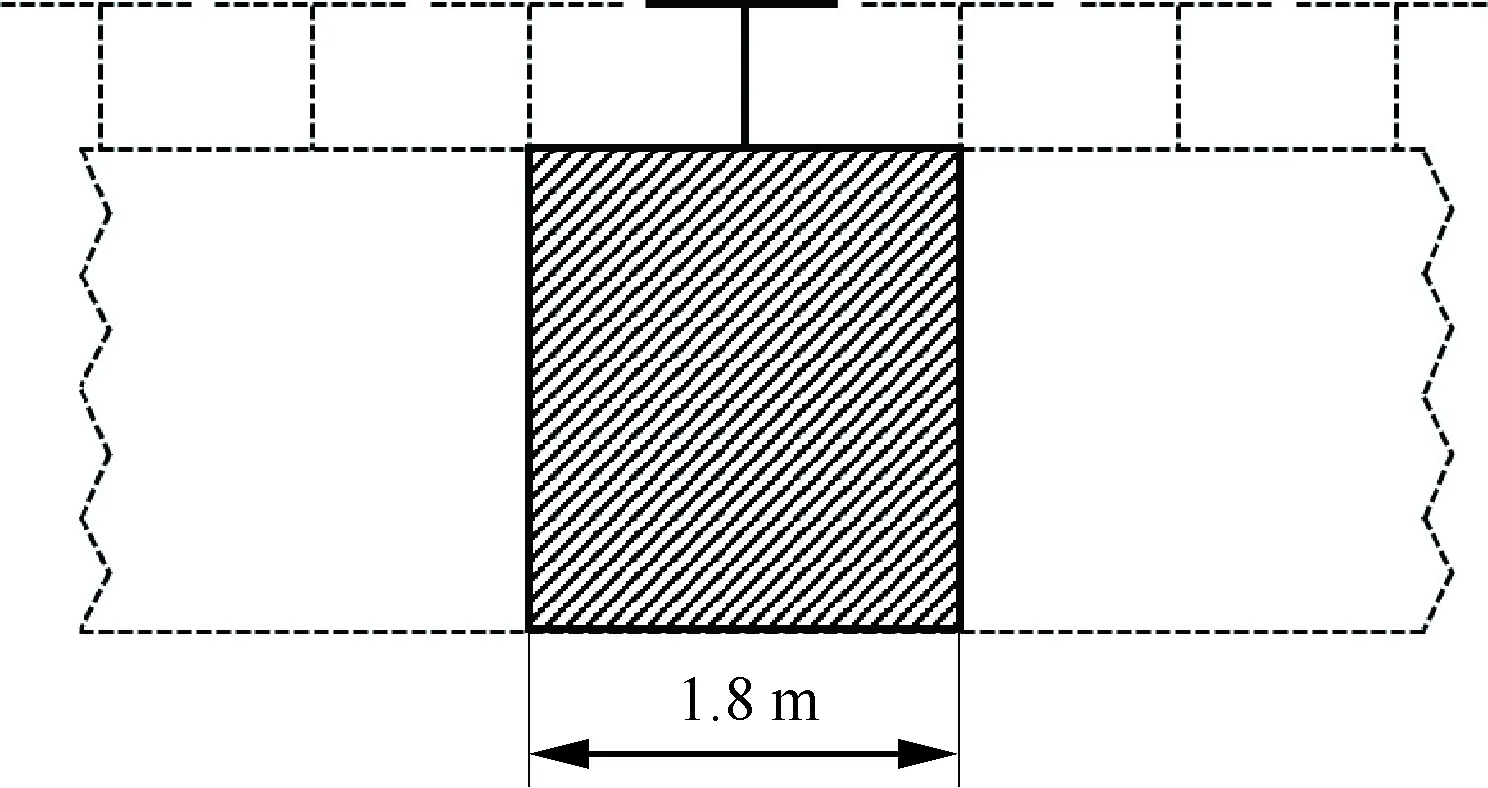
图17 螺旋桨/机翼翼段示意图Fig.17 Propeller/wing section sketch

2.3.1 问题描述与方法

由上文研究可知螺旋桨滑流影响可以被理解为螺旋桨做功对远场来流的加速作用与旋转效应的叠加，因此分别选取与单独螺旋桨中心位置及两侧0.6倍桨半径位置处的特征截面翼型进行外形轮廓的最优匹配设计，也即针对螺旋桨滑流影响下由螺旋桨中心截面翼型、上洗侧特征截面翼型及下洗侧特征截面翼型共3个翼型所构成的机翼翼段进行优化设计。

采用与2.2.1节相同的翼型参数化方法对各特征截面翼型进行建模，共选取5个控制点对翼型前半段曲率变化进行控制，各控制点相对翼型弦长的位置分别为：0.05、0.1、0.15、0.3、0.5，各控制点对应扰动函数中的n均取为3。设计过程采用与上文低雷诺数翼型优化相同的约束条件、优化目标及设计流程，也即将2.2.1节低雷诺数翼型优化设计问题中的设计对象由低雷诺数翼型换作机翼翼段即可，具体优化设计过程将不再赘述。

2.3.2 结果与分析

图18为基准翼型(Base Airfoil)、螺旋桨中心截面优化翼型(Optimal Center Airfoil)、上洗侧特征截面优化翼型(Optimal UWS Airfoil)及下洗侧特征截面优化翼型(Optimal DWS Airfoil)之间外形轮廓对比。由图可以看出，与基准翼型相比，螺旋桨中心截面优化翼型最大厚度位置相对基本保持不变，翼型头部附近区域弯度相对增大，同时翼型后缘附近区域反弯度亦相对稍有增大。而与螺旋桨中心截面优化翼型相比，上洗侧特征截面优化翼型前半段相对弯度有所减小，翼型头部变得尖锐，且上表面由前缘向下游区域发展段过渡更加圆润，下洗侧特征截面优化翼型前半段相对弯度则有所增大，翼型头部变得饱满，上表面由前缘向下游区域发展段曲率变化较为明显，且翼型最大厚度位置也稍有前移。

表5为单独螺旋桨滑流影响下近似高雷诺数流态区域内机翼翼段优化前后的气动特性参数对比。可以看出，与基准机翼翼段相比较，优化翼段升阻特性得到显著改善，其中升力相对增大约9.83%，阻力相对降低约9.15%，升阻比则相对增大达20.88%。此外，优化后机翼翼段抬头力矩有所增大，优化前后俯仰力矩参数之间相对偏差为7.30%，满足约束条件。

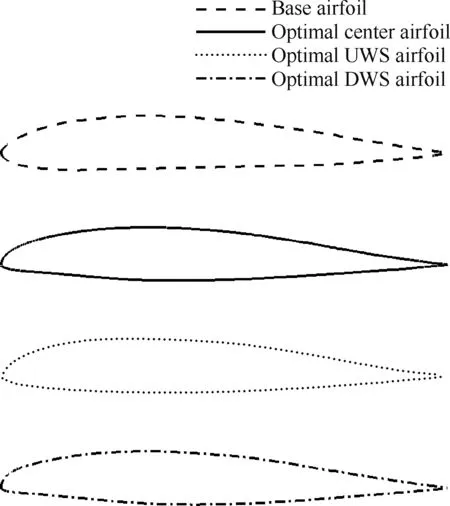
图18 优化前后机翼翼段特征截面翼型外形轮廓对比Fig.18 Comparison of characteristic sectional airfoil profile used for wing section modelling before and after optimization

表5 单独螺旋桨滑流影响下机翼翼段气动特性对比

Table 5 Comparison of aerodynamic performance of wing section under the isolated propeller-induced effects

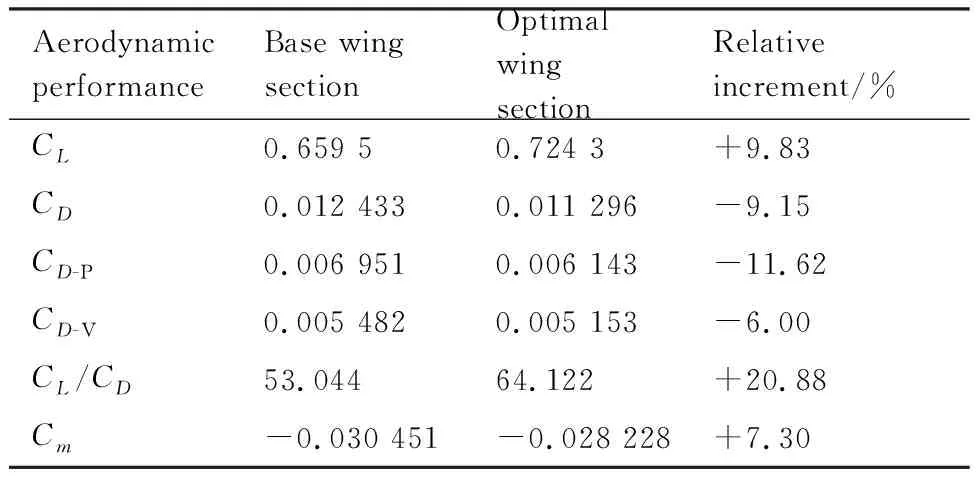
Aerodynamic performanceBase wing sectionOptimal wing sectionRelative increment/%CL0.659 50.724 3+9.83CD0.012 4330.011 296-9.15CD-P0.006 9510.006 143-11.62CD-V0.005 4820.005 153-6.00CL/CD53.04464.122+20.88Cm-0.030 451-0.028 228+7.30

图19为基准机翼翼段与优化机翼翼段分别在单独螺旋桨滑流影响下各特征位置截面翼型压强分布对比。由图可以看出，基准机翼翼段各特征截面受螺旋桨加速及旋转效应影响极为显著，3种特征位置翼型前半段计算压力分布形态差异较大，其中气流上洗侧特征截面翼型前缘计算压力分布陡且急，吸力峰值相对最大，螺旋桨中心截面翼型次之，气流下洗侧特征截面翼型前缘计算压力分布相对最为缓和且吸力峰值亦相对最小，这表明基准翼段沿展向存在较强的压力梯度，而为了克服该逆压梯度机翼近壁面流动还需要消耗额外的能量，进而造成总压损失或压差阻力较大。优化机翼翼段各特征截面翼型前缘吸力峰值则较为相近，沿展向压力梯度分布均匀，压差阻力显著降低，阻力特性得到明显改善，同时优化机翼翼段前半部分弯度相对增大亦使得其下表面压力有所增大，机翼翼段升力特性亦有所改善。

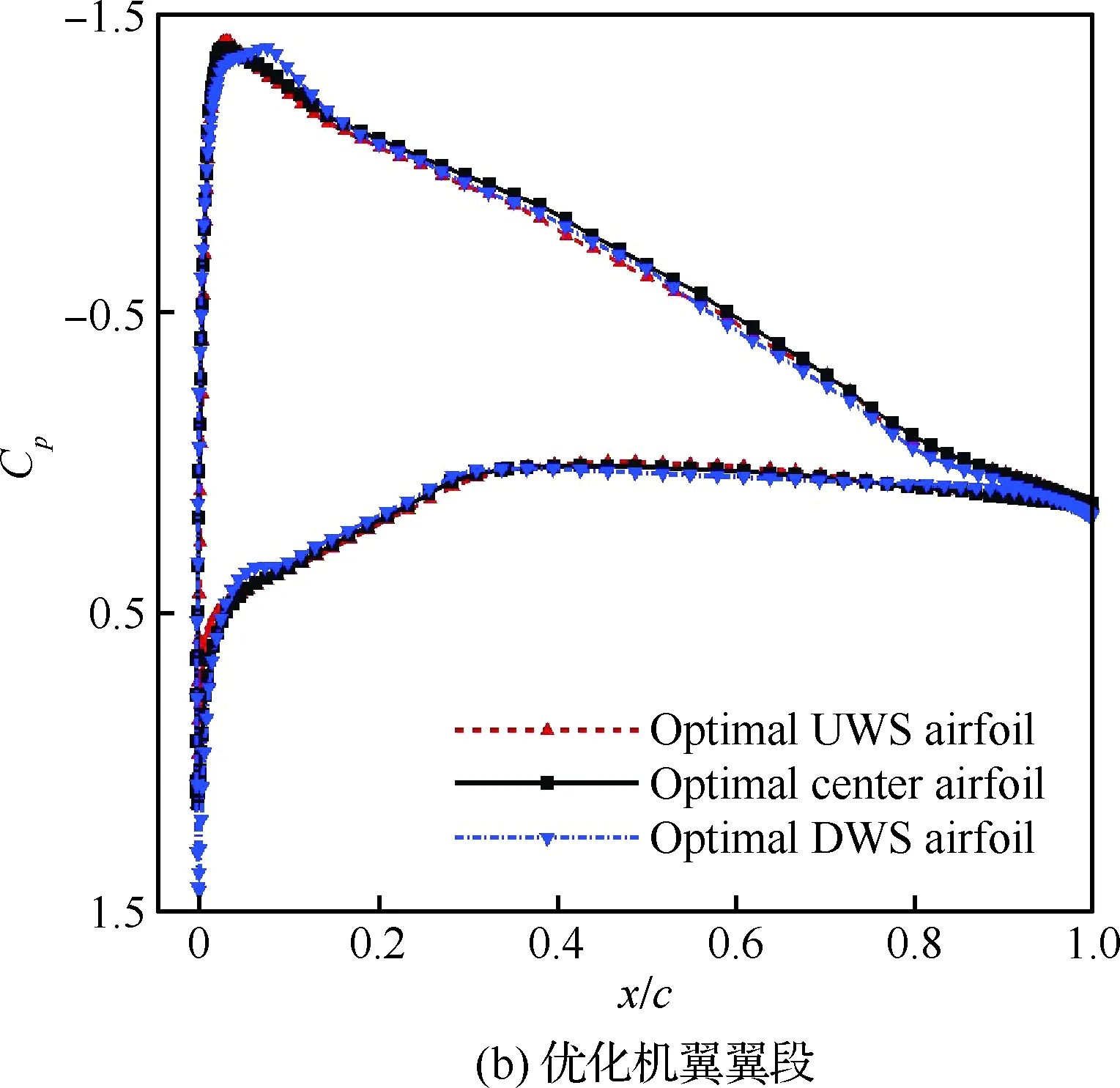
图19 特征截面翼型压力分布对比Fig.19 Comparison of pressure distribution around characteristic sectional airfoils

3 气动设计结果及分析

为了验证所提出低雷诺数多螺旋桨/机翼耦合设计思想及设计方法的有效性及可靠性，将进行多螺旋桨/机翼耦合设计得到的设计结果与常规仅进行低雷诺数翼型设计得到的设计结果进行对比分析。表6给出设计状态下3种不同构型机翼气动特性计算结果。其中“Optimal Wing”表示采用2.2节二维翼型设计结果构造的不考虑螺旋桨滑流影响的干净机翼模型，“Optimal Wing+ Base Configuration”表示在“Optimal Wing”模型基础上引入对如图1所示四螺旋桨/机翼基准构型所对应螺旋桨转速状态下的滑流影响，“Optimal 3D Wing+ Optimal Configuration”表示经过本文多螺旋桨/机翼耦合设计后得到的最终方案模型。

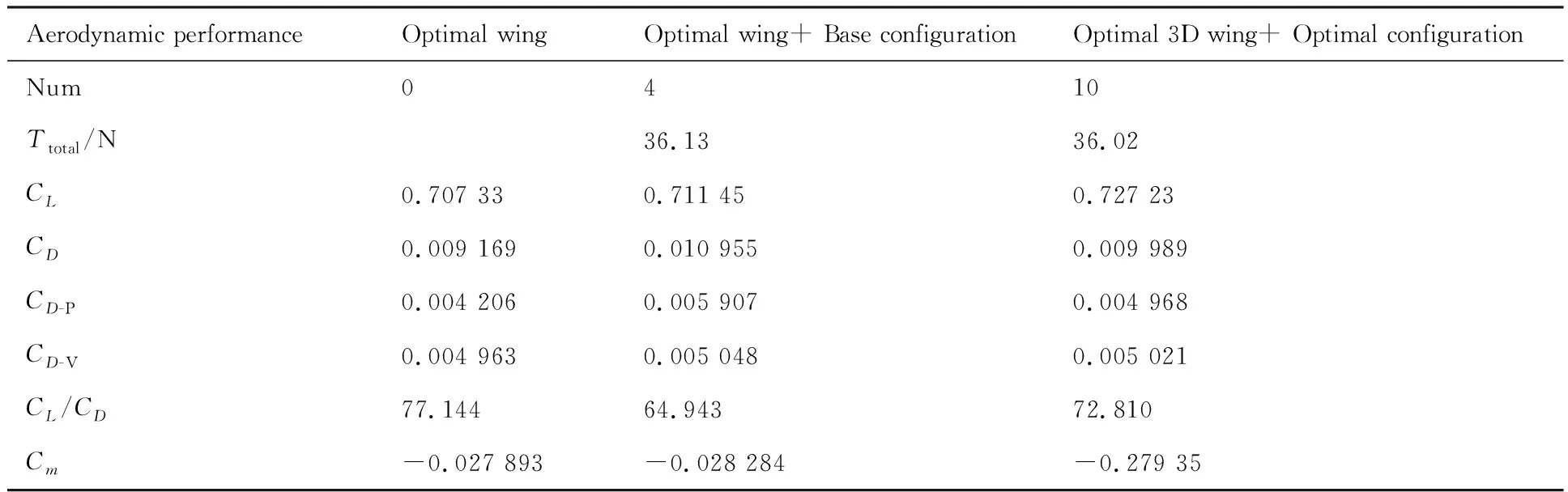
表6 不同构型机翼气动特性对比

由表6可以看出：① 对于Optimal Wing模型而言，当引入四螺旋桨/机翼基准构型滑流影响时，其升力相对有所增加，但阻力亦相对显著增大，其中压差阻力增量占总阻力增量约95.2%，机翼升阻比亦因此相对降低达15.8%，这与表2中基准构型滑流影响下的机翼升阻特性恶化程度(16.32%)相当，也就是说，常规不考虑螺旋桨滑流影响而仅进行低雷诺数翼型设计的思路与方法仅仅是将机翼本身的气动特性进行了一定的改善，而并不能从根源上对螺旋桨滑流的不利影响进行抑制或消除；② 与Optimal Wing+ Base Configuration模型相比较，Optimal 3D Wing+ Optimal Configuration模型在满足纵向力矩特性差异不超过10%的约束条件的同时，其计算升力相对有所增大，计算阻力则相对显著降低(约8.8%)，其中压差阻力减小量约占总阻力减小量的97.2%，机翼升阻比相对增大达12.1%，升阻特性得到显著改善，这表明通过本文多螺旋桨/机翼耦合设计能够得到相对常规仅进行低雷诺数翼型设计显著更优的设计结果；③ 与Optimal Wing模型相比较，Optimal 3D Wing+ Optimal Configuration模型在满足纵向力矩特性差异不超过10%的约束条件的同时，其计算升力及计算阻力均相对有所增加，机翼升阻比则相对稍有降低(约5.6%)，而结合Optimal Wing+ Base Configuration模型升阻特性即可看出，通过本文多螺旋桨/机翼耦合设计，能够对因螺旋桨滑流带来的不利气动影响提供约64.5%的有效补偿。