高鲁棒性的螺旋桨片条理论非线性修正方法

2018-08-29范中允周洲祝小平王睿王科雷

航空学报 2018年8期

范中允，周洲,*，祝小平，王睿，王科雷

1. 西北工业大学航空学院，西安 710072 2. 西北工业大学无人机特种技术重点实验室，西安 710065

垂直起降无人机成为现代无人机领域的一个重要研究方向。小型垂直起降无人机以定距螺旋桨为主要推进装置，螺旋桨的气动特性优劣将对无人机的飞行性能有较大影响。然而，垂直起降无人机螺旋桨的设计需要兼顾悬停和巡航状态，至少包含两个设计点，同时工作状态跨度较大，对螺旋桨的分析设计工具提出了大跨度、高鲁棒性的要求。

CFD时间代价过大，难以直接用于迭代设计，片条理论(也称叶素动量理论，BEMT)由于其计算效率高而被广泛用于螺旋桨设计。片条理论由来已久，目前已有许多关于其修正或改进方法的研究。2005年，Martínez 等[1]依据4组试验结果提出了一种无自由参数的叶素理论修正模型。2007年，Hunsaker[2]针对垂直起降无人机的设计问题，提出将叶素理论与计算流体力学的动量方程相结合，对螺旋桨周围的诱导流场进行低计算代价的数值模拟，并去掉了小迎角假设。2009年，Dossing[3]在叶素理论中加入了尾迹旋转和扩张修正，以改善在桨尖和桨根的预测精度。2010年，Rwigema[4]为了考虑滑流对螺旋桨的影响，在叶素动量理论的基础上将一段涡管加入到螺旋桨后部。Vaquero等[5]以叶素动量理论结果为参考，进行了低雷诺数桨叶特性的试验研究。2012年，Whitmore和Merrill[6]将叶素动量理论推导中的小迎角假设去掉并进行了理论推导，以得到能够考虑大迎角的叶素动量理论。Burdett和Van Treuren[7]对比了叶素理论和叶素动量理论对于桨叶扭转角设计的影响，发现两种理论的设计结果在桨毂扭转角差别约15°，功率系数相差0.08。2013年，Ding等[8]将Wilson模型与叶素理论相结合进行了桨叶设计。2016年，El Khchine和Srili[9]提出一种将CFD方法与叶素动量理论方法相结合的数值模拟方法，以减小CFD的计算代价。2017年，Barnes[10]为了改善螺旋桨载荷分布的精度，将叶素理论与螺旋形尾迹相结合，并将叶素理论与升力线理论相结合以考虑后掠桨叶在跨声速的性能。Dumakude和Kamper[11]结合轴向和径向诱导因子，将叶素动量理论和CFD的计算结果进行了对比和分析。

尽管国内外学者已经对提高片条理论精度和非线性修正进行了大量研究，但这类研究多是针对螺旋桨的常规工作段，在极端条件下的计算稳定性问题却鲜有研究。同时，鉴于螺旋桨与机翼/机体的耦合设计趋势，螺旋桨分析工具要能够提供更多的流场信息，如环量分布及诱导速度场，在这方面基于片条理论的研究也有所欠缺。在极端工况下，如静止及高前进比状态，实践证明片条理论的计算稳定性和环量预测精度都将下降，这是由于理论公式中存在着解的不确定性问题。因此，需要对片条理论计算稳定性和环量分布的特性进行更加深入的研究。

另一方面，在片条理论中，叶素的气动特性将直接影响所得螺旋桨的气动特性，螺旋桨的非线性特性主要由叶素的非线性体现，因此在计算时需要考虑叶素的大跨度、多重非线性的因素。例如，当在悬停状态时，螺旋桨工作在很低前进比下，部分叶素的当地迎角很大甚至已经发生分离；大多数小型无人机的螺旋桨都工作在低雷诺数状态下，而在平飞过程中螺旋桨的桨尖马赫数也到了需要考虑压缩性的范围。

对于叶素气动模型，Carroll和Marcum[12]针对叶素分离状态进行了叶素动量理论与CFD方法的结果对比。Morgado等[13]提出了一种根据翼型前缘半径拓展大迎角翼型气动特性的方法，可将翼型大迎角模型范围提高到90°。Dorfling和Rokhsaz[14]为了改进叶素理论在非线性区域的计算精度，提出了一种用于叶素理论的翼型非线性气动模型，预测迎角可以达到90°，同时进行了压缩性修正。Kown等[15]使用二维CFD方法在特定雷诺数下建立了截面翼型升阻系数随迎角变化的气动数据库,并用于叶素动量理论。Macneill和Verstraete[16]针对小尺寸无人机螺旋桨的低雷诺数和桨叶失速问题，对翼型建立了大范围的迎角和雷诺数数据库，并进行了旋转效应的处理。

可以发现，叶素动量理论的叶素气动数据，主要由两种方法获得：一是用简单的翼型气动力模型，这种方法拓展性较好，而适应性有限，虽然大迎角特性可以较好体现，但是压缩性、低雷诺数特性反映有限；二是建立翼型数据库，可以使用CFD或者风洞数据，这种方法在数据点充足的情况下准确性较好，在维度较低时使用广泛，但是倘若参数较多、非线性较强时，对未知函数形状的高维插值或拟合存在困难，同时逐渐增大的数据量，使得数据存储和使用也越来越复杂。因此，在考虑翼型多维度的多重非线性时，气动模型需要进行改进。

针对以上两方面的问题，作为翼型数据库方法的延伸，本文首先建立人工神经网络(Artificial Neural Network, ANN)对翼型不同状态下的非线性效应进行特征提取，解决了翼型多维度的多重非线性气动特性快速预测的问题；然后基于上述模型，分析了片条理论在极端状态下的局限性，提出了一种环量迭代修正方法，解决了极端环境下片条理论计算稳定性问题和解的奇异性问题。最后，通过试验数据和CFD方法，对本文提出的片条理论修正方法进行准确性及鲁棒性验证。

1 基于神经网络的翼型气动分析模型

叶素气动特性的准确性将直接影响片条理论的准确性。本文利用神经网络优异的无先验函数非线性拟合能力，来兼顾多种翼型非线性气动特性和较高的预测响应速度。拟建立BP(Back Propagation)人工神经网络，作为翼型气动特性预测模型，并对其性能进行验证分析。

1.1 神经网络模型

神经网络的基本原理已经有诸多论述[17]，本文不再赘述。典型的BP神经网络构型如图1所示，包括一个输入层x1,x2,…,xn、一个输出层o1,o2，…，on和若干隐含层。适当增加隐含层或增加隐含层结点可以提高神经网络对数据非线性的捕捉能力。考虑到螺旋桨叶素气动模型有多重非线性问题，本文选用双隐含层的神经网络结构。

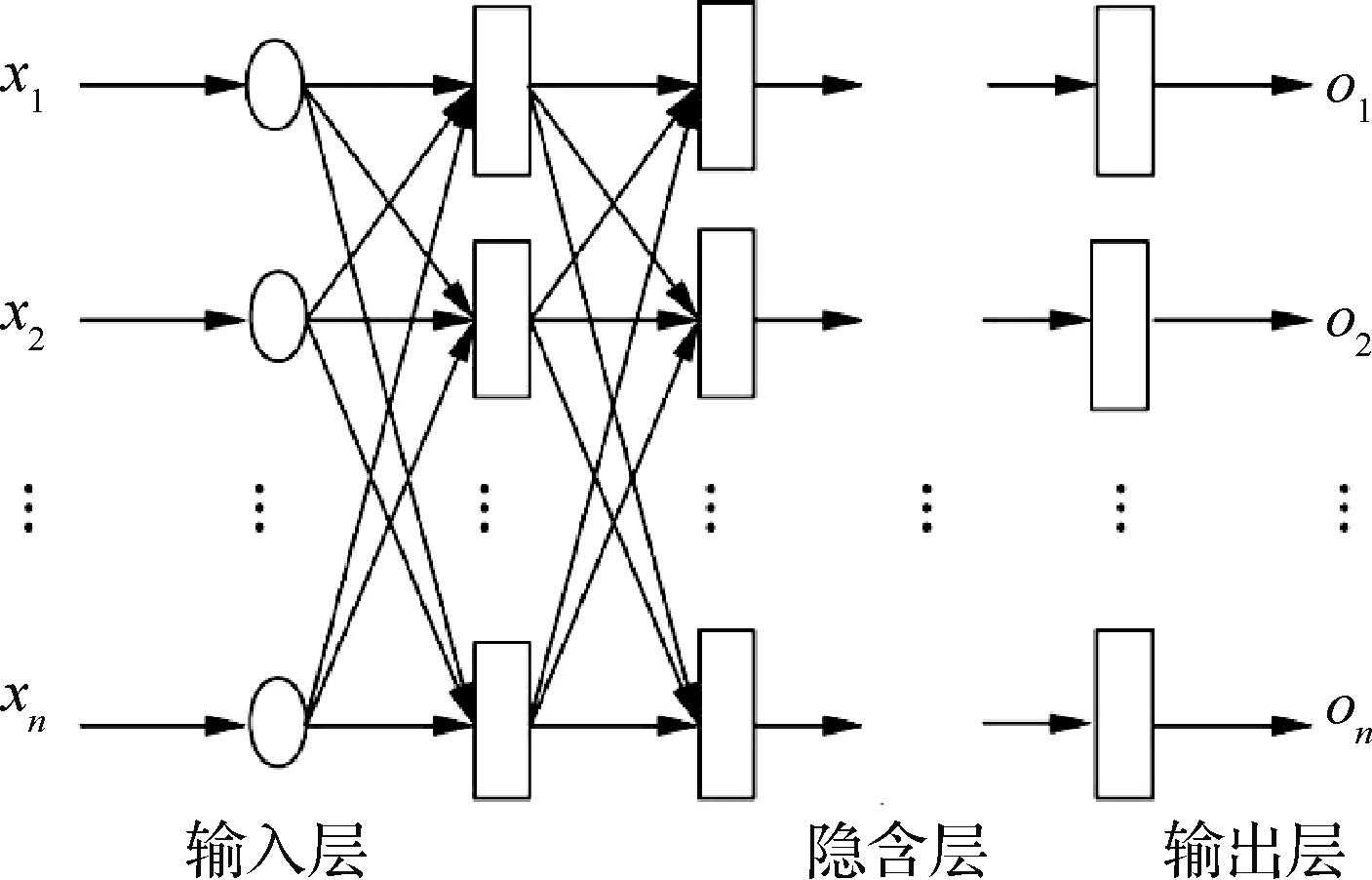
图1 BP神经网络框架Fig.1 Framework of BP neural network

构建形如图1所示的4层神经网络结构，网络输入量为雷诺数Re、马赫数Ma、迎角α，输出量为升力系数CL、阻力系数CD、力矩系数Cm。选取第一隐含层结点数12个，第二隐含层结点数16个。隐含层的传输函数选用双正切Sigmoid函数[18]，输出层为线性传输函数。尽管在本文的片条理论计算中没有用到叶素力矩系数，但考虑到将来研究螺旋桨变距特性时的需要，本文仍然将力矩系数包含在神经网络结果内进行分析。

作为初步研究，以螺旋桨常用的经典翼型Clark Y作为样本翼型，均布计算样本共616个，在迎角维度上插值加密，最终样本点数目共计1 463个。选取样本参数范围为：雷诺数Re=0.6×105～40×105，马赫数Ma=0.05～0.55，迎角α=-3°～15°。采用CFD方法进行样本特性计算，使用结构化网格，网格量为2.7万，网格质量大于0.7，正交性大于0.8，选择剪切应力输运(SST)k-ω湍流模型。

1.2 神经网络性能验证

本节就气动特性预测、非线性特征提取和包线拓展3个方面的性能，对所构建的Clark Y翼型气动特性分析模型进行验证。

1.2.1 气动特性预测

通过交叉验证检查发现，相对误差较大的点一般在数值接近0或迎角大于10°(非线性较强)的位置。为了直观反映神经网络预测的准确性，选择雷诺数Re=3.0×105、马赫数Ma=0.4 的状态，预测结果随迎角的变化曲线如图2所示。

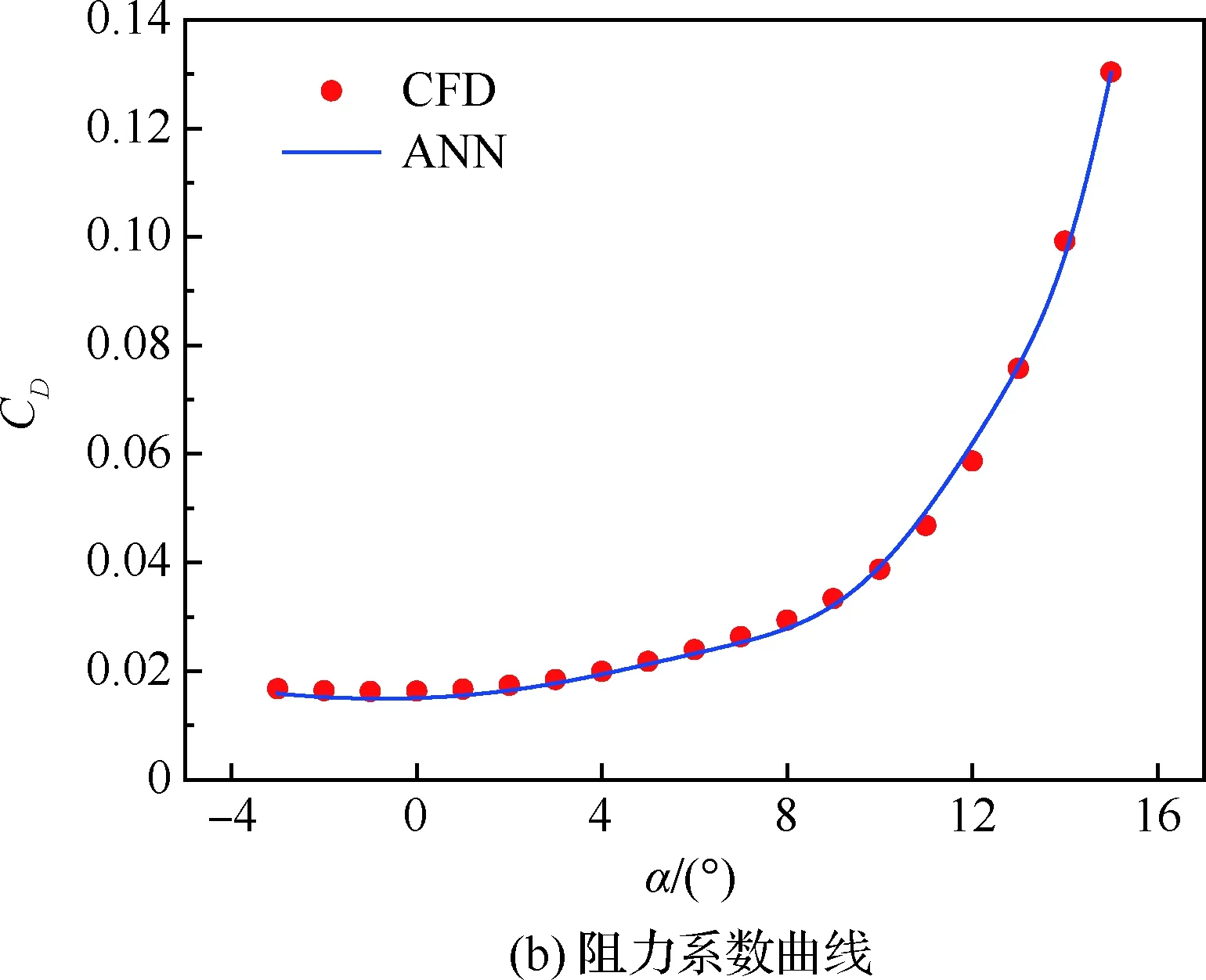
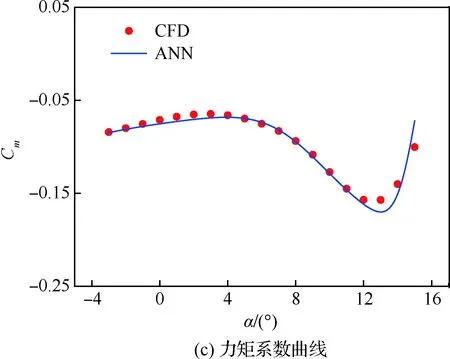
图2 气动系数随迎角的变化曲线 (Re=3.0×105, Ma=0.4)Fig.2 Change curves of aerodynamic coefficients with angle of attack (Re=3.0×105, Ma=0.4)

由图2可知，升力系数和阻力系数的预测值与CFD吻合度较高，尽管神经网络对力矩系数的预测在数值上有一定误差，但是其变化规律是一致的。

1.2.2 非线性特征提取

图2已经展示了神经网络对迎角非线性特征的良好捕捉能力，图3为不同雷诺数和不同马赫数下的神经网络预测曲线。

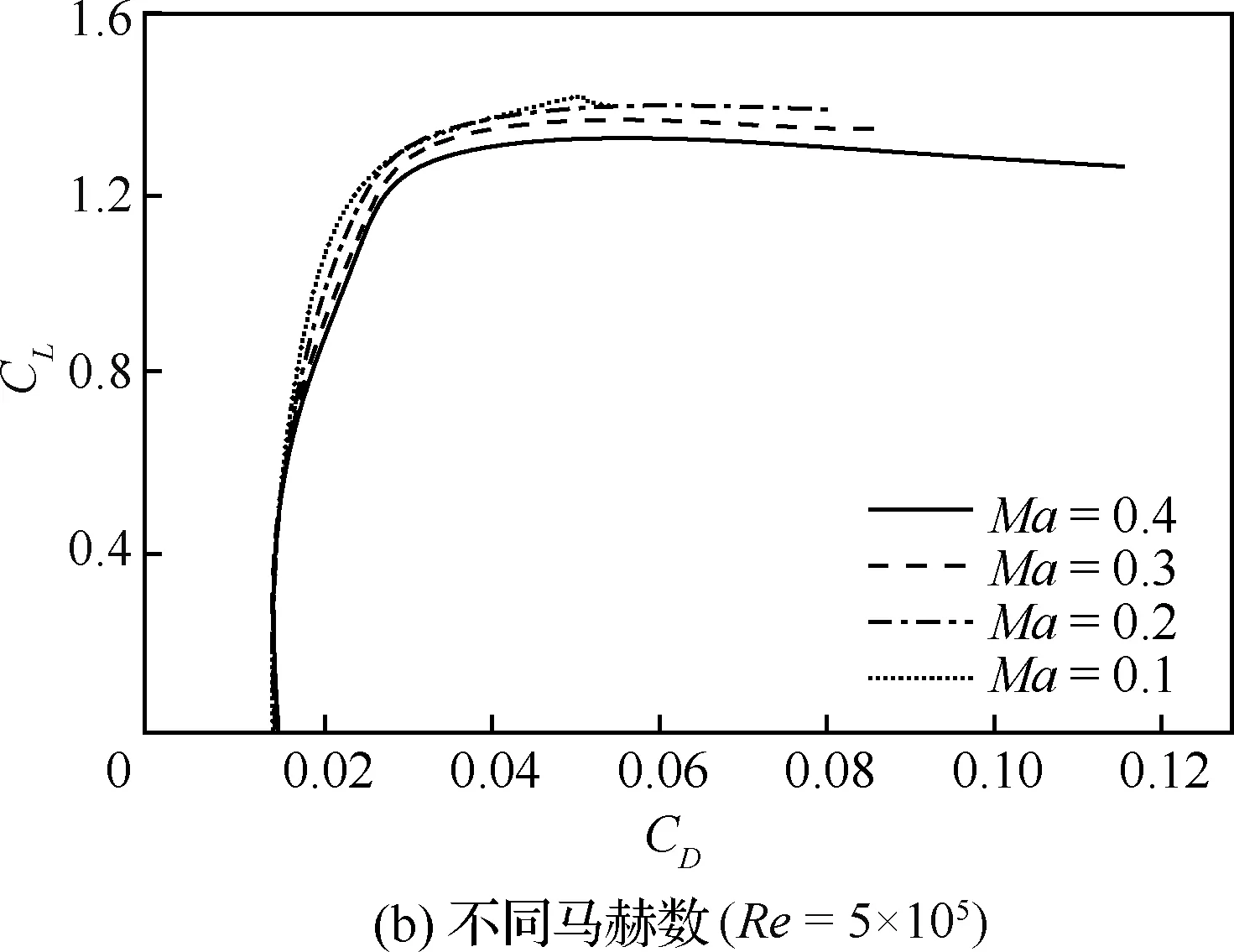
图3 神经网络预测升阻极曲线Fig.3 Prediction of CL vs CD polar curves of neural network

由图3(a)可以看出，雷诺数降低，零升阻力增大，最大升力系数减小，升阻比减小，升力线斜率略有降低。神经网络的预测结果与Silverstein[19]对Clark Y翼型的研究结果一致。由图3(b)可以看出，马赫数增加，零升阻力略有增加，升阻比降低，最大升力系数减小，随着迎角增大马赫数的影响变大。神经网络可以反映翼型气动性能在不同马赫数下的变化特征。

1.2.3 包线拓展

在小型螺旋桨计算分析时，不可避免地会触及计算边界。许多小尺寸螺旋桨桨叶雷诺数常在6.0×104以下，这一边界是最容易超越的。本节以雷诺数下限为例，说明神经网络对外插的适应性问题。图4为Re=1×104～6×104下的神经网络预测曲线。

图4 超过雷诺数下限时的气动系数曲线(Ma=0.1)Fig.4 Aerodynamic coefficient curves for Re over the lower limit (Ma=0.1)

在迎角小于约8°时，预测结果趋势仍然合理。迎角大于8°以后，大迎角非线性特征过强，外插预测结果出现震荡，因此在本文中大迎角的超包线使用将被严格限制。

2 螺旋桨片条理论修正方法

Veldhuis[20]及刘沛清[21]均已经对螺旋桨的片条理论方法进行了详细的推导。本节针对理论在应用时的奇异性和不稳定性，结合涡流理论进行修正方法研究，并对修正方法有效性进行验证。

2.1 基本片条理论及其局限性

片条理论是一种由二维到三维的计算方法。图5为螺旋桨叶素的受力及速度分解图。图中:V0为来流速度，β为干涉角，Vt为环向诱导速度，Va为轴向诱导速度，α为实际迎角,V′为诱导螺距增量，φ和φ分别为几何入流角和实际入流角，Ω为角速度，r为叶素半径，Vgeo、Vreal分别为几何入流速度、实际入流速度，γ为阻升角，dR、dL、dD、dT、dF分别为叶素剖面合力、升力、阻力、拉力、扭力。如图5所示，叶素的实际迎角受诱导速度影响，减小了β。在给定计算条件下，图中的β、Vt、Va是未知的。

为了求解β，结合叶素理论和动量理论可以推导出隐式方程[21]：

(1)

(2)

(3)

(4)

式中：σ为实度；NB为桨叶数；b为叶素弦长；ns为转速。

由隐式方程式(1)求得干涉角后，可由文献[21]中的公式求得螺旋桨的拉力、扭矩和功率。

在非线性不强、前进比适中的条件下，传统片条理论方法能够较好地处理绝大多数的螺旋桨分析计算问题。然而，极端状态下片条理论的计算稳定性不足。

一方面，在片条理论中，求解拉力系数、扭矩系数都是基于一个轴向速度干扰系数a：

(5)

但是当升力系数趋于0时(CL→0)，有

tanφtan(φ+γ)→tanφtan(φ+90°)=-1

图5 螺旋桨叶素受力分析Fig.5 Blade element forces analysis of propeller

那么轴向速度干扰系数将会趋于无穷大(a→∞)，这将导致在高前进比、拉力很小时，诱导速度计算结果容易出现奇异性。因此，若直接由传统片条理论获得诱导速度，其只能用于低前进比状态。

另一方面，片条理论在极端状态下存在非物理解。例如，图6为很低和很高前进比下片条理论计算得到的环量Γ分布。其中，螺旋桨模型均为JXF16×8，高度H=400 m。

图6(a)为来流速度V0=0.1m/s、转速ns=948.65 r/min状态下的环量分布，图6(b)为来流速度V0=11.11 m/s、转速ns=2 200 r/min状态下的环量分布。图中r/R表示桨叶剖面半径与螺旋桨半径的比值，表征剖面的径向无量纲站位。图6(a)所示状态几乎是静止状态，叶素的几何迎角很大，已经进入非线性区；图6(b)所示状态则是高来流速度、低转速状态，叶素的几何迎角较小，产生小量的负拉力。两图环量分布均在某一径向位置突变为零，而其他径向位置计算正常。然而该处叶素的几何迎角并非零升迎角，会产生有限值的升力或环量，因此计算所得环量或升力系数与叶素所处状态不符，更与实际的桨叶环量分布不符。

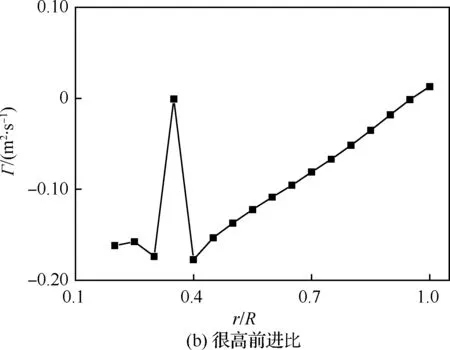
图6 螺旋桨桨叶环量分布Fig.6 Circulation distribution of propeller blade

分析原因可以发现，干涉角方程式(1)的解是不唯一的。当升力系数趋于0(CL→0)时，式(1)右边的分母会趋于无穷((1-tanγtanβ)→∞)。这使得实际迎角为零升迎角(CL==0)的干涉角恒为方程的解之一。因此，当方程的解使得实际迎角为零升迎角(CL==0)时，当地叶素的环量也计算得零，而这与叶素所处的实际流动状态不符。这表明，该隐式方程的解是不唯一的，存在没有物理意义的解。当计算得到的解是非物理解时，所得到的桨叶环量分布会在某些剖面突然降为零，即得到与实际不符的结果。

这一现象降低了片条理论对极端状态的计算鲁棒性和可靠性。编程实践发现，螺旋桨在很低或很高前进比下更容易出现上述问题。分析原因可能如下：

1) 很低前进比下剖面翼型处于大迎角状态，非线性较强，升力系数在真实干涉角解附近不单调，导致数值求解方法很难找到真实解，相比之下非物理解更容易找到。

2) 很高前进比下，剖面翼型的实际升力系数很小，与零升迎角对应的非物理解极为接近，导致数值求解时无法分辨，从而解出非物理解。

非物理解的干涉角正好使得当地叶素升力为零，而升力为零对应的诱导速度也为零，诱导速度引起的干涉角也为零，那么叶素所处的实际迎角便不为零，会产生有限值的升力。由此可见，非物理解在其本身是自相矛盾的，其对应的干涉角、升力系数、诱导速度、实际迎角等参数之间互不匹配。

2.2 片条理论修正方法

由于非物理解导致各参数不匹配，考虑采用各参数相互迭代计算的方法以使之逐渐协调。因此，本节结合涡流理论相关方法，构建了如图7所示的环量迭代框架。首先将片条理论得到的环量作为环量初值，由涡流理论求得诱导速度，再由几何关系求得干涉角，进而得到实际迎角及升力系数，由升力系数又可以得到桨叶环量。如此反复迭代直到桨叶环量的残差小于给定值。

图7 环量迭代流程Fig.7 Iteration flow falt of circulation

在环量迭代框架中，涡流理论与片条理论相互结合、互为补充，框架仍然采用片条理论以干涉角为核心的计算思路，但计算公式借用涡流理论方法进行推导。为了使框架更加完整、清晰，下文给出在迭代过程中所需的环量、诱导速度、诱导速度修正、拉力和扭矩的求解方法。

1) 环量

在不考虑叶素阻力的情况下，环量计算式为

(6)

式中：T(r)为半径r处叶素单位展长的拉力；ρ为空气密度。由于拉力中包含阻力分量，因此当拉力较小即剖面升阻比较低时，会引起较大的误差。本文直接使用当地剖面翼型升力系数来得到环量，即

(7)

式中：Vlocal为当地来流速度(包含诱导速度)。

2) 诱导速度

国内外对涡流理论已有诸多论述[22]。按照涡流理论方法的推导，桨盘处的诱导速度与当地环量Γ的关系为[22]

轴向诱导速度：

(8)

环向诱导速度：

(9)

在公式推导中，假设V′沿径向不变。这一假设仅在贝兹的螺旋桨最高效率条件[21]下才成立。为了得到变化的V′，本文根据图5进行了几何分析和公式推导。由叶素速度分量的几何关系可得

(10)

V′-Va=Vttanφ

(11)

代入诱导速度式(8)和式(9)可得

(12)

化简后得到

(13)

当沿桨叶的环量分布已知时，即可迭代求解该隐式方程得到V′。值得一提的是，当给定V′时，即可得到环量Γ沿半径r的分布，而这个环量分布即为无限桨叶数、不计叶素阻力时的螺旋桨贝兹最佳环量分布。

若假设合成诱导速度(Va+Vt)与真实入流速度Vreal相互垂直[23]，则可以得到

(14)

由于按式(9)求解环向诱导速度较为简单，因此可根据式(14)求出轴向诱导速度Va，但是，真实入流角φ事先是未知的，式(14)无法直接使用，因此本文将用隐式方程式(13)的解作为初值求出干涉角，得到φ的初值后再使用式(14)求解。

3) Prandtl桨尖/桨根修正

由于片条理论及涡流理论均使用了桨盘平均假设，其计算所得诱导速度是桨盘平均值。若将Prandtl修正的机理看作修正由桨盘平均引起的误差，那么Prandtl的桨尖/桨根修正系数可以作用在桨叶诱导速度上[23-24]。修正公式为[23]

(15)

(16)

(17)

(18)

4) 拉力和扭矩

根据叶素受力分析可得剖面拉力dT和扭矩dM为

dT=(ρΓVt-dDsinφ)dr

(19)

dM=(ρΓVa+dDcosφ)rdr

(20)

为了将式(19)和式(20)中的阻力分量项换成与环量项相同的形式，作如下假设：参照环量的定义，定义假想矢量“阻量”ΓD。环量矢量Γ的方向垂直于来流速度矢量V，而阻量ΓD的方向则沿着矢量V：

(21)

(22)

(23)

阻量同样可以进行矢量运算，给定环量下的剖面拉力和扭矩分别为

(24)

(25)

获得剖面的拉力和扭矩后沿桨叶积分即可得到螺旋桨拉力和扭矩。

2.3 环量迭代方法验证分析

为说明环量迭代修正方法对片条理论非物理解、不稳定性的修正效果，本节根据计算实践中遇到的错误点，以JXF16×8螺旋桨为对象，将桨叶由0.2R～R间隔0.05等分17个截面，选取极端状态进行传统方法和改进方法的对比。图8中，BEMT是传统片条理论计算结果，pBEMT是仅仅加入Prandtl修正的片条理论计算结果，rBEMT是本文提出的环量迭代修正后的结果。

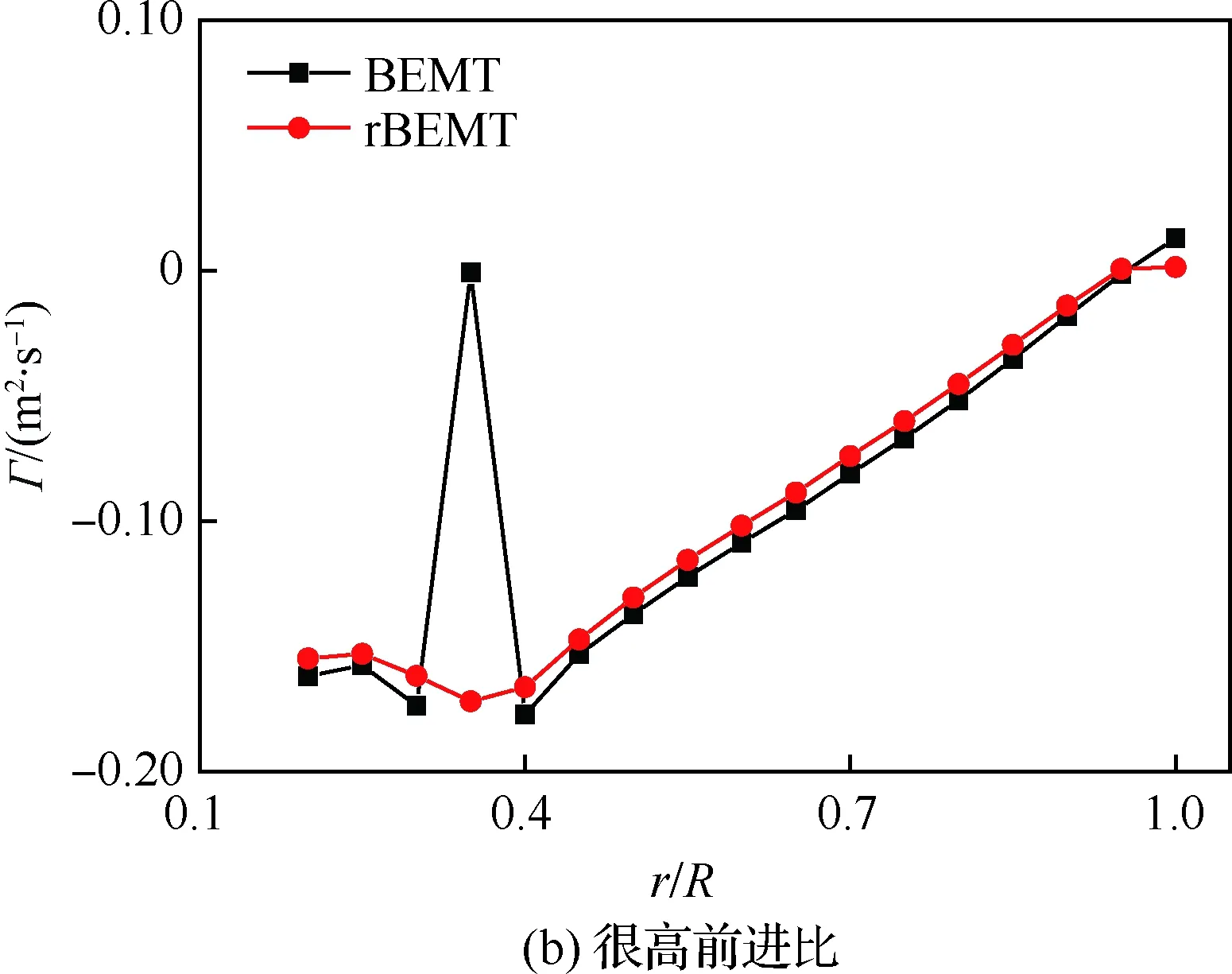
图8 桨叶环量分布对比Fig.8 Comparisons for blade circulation distribution

2.3.1 很低前进比计算验证

选取很低前进比的计算状态：V0=0.1 m/s、转速ns=948.65 r/min，前进比J=0.016，高度H=400 m。图8(a)为该状态下修正前后的环量分布图。在此状态下，叶素的非线性效应较强，传统片条理论的叶素干涉角求解方法更容易找不到合理解。图示状态在径向位置r=0.5R处得到了非物理的解，使得此处的升力系数为零，从而环量在此处突变为零，显然不符合事实。通过前述环量迭代方法，干涉角逐渐与其他参数相协调，彻底消除了环量分布的突变。

2.3.2 很高前进比计算验证

选取很高前进比的计算状态：V0=40 km/h、转速ns=2 200 r/min，前进比J=0.745 6，高度H=400 m。图8(b)为该状态下修正前后的环量分布图。在此状态下，剖面翼型的当地迎角很小，真实升力系数很小，隐式方程式(1)的真实解与非物理解比较接近，数值计算更加难以分辨真实解与非物理解。图示环量在r=0.35R处突变为零，而环量迭代使得干涉角与安装角、升力系数相容，从而消除了环量的突变。

2.3.3 环量迭代对比分析

选择计算状态：V0=0.1 m/s、转速ns=4 000 r/min，前进比J=0.003 69，高度H=400 m。图8(c)为该状态下修正前后的环量分布图。从修正前后的对比可以看出，传统方法在桨根处由于非线性较强产生了轻微波动，而修正后环量变得更加平滑；迭代修正后环量比修正前环量整体偏高，尤其在桨尖比单纯使用Prandtl修正时偏高明显。本文和文献[15]的计算实践表明，片条理论计算所得拉力和功率一般低于试验值(小拉力状态除外)，由于环量迭代修正使得环量增大，因此修正后的计算结果更加接近实际值。

3 修正片条理论方法验证

为说明本文方法在正常和极端状态下都具有较好的准确性和计算鲁棒性，本节结合项目试验和CFD方法，以JXF16×8榉木螺旋桨为主，对比说明本文修正后的片条理论在零来流、高空高速等极端状态下都具有较好的鲁棒性。同时，为了说明本文修正方法与几何模型无关，对其他螺旋桨和流动状态差异较大的旋翼均具有普适性，选取Falcon16×10碳纤维螺旋桨和某1.5 m直径旋翼，辅助说明本文计算方法对不同对象均具有同样的鲁棒性和准确性。

3.1 JXF16×8螺旋桨算例

1) 螺旋桨车载试验

JXF16×8螺旋桨是一种成熟的榉木螺旋桨商品，结合项目需要进行了螺旋桨车载试验。图9为螺旋桨车载试验系统的示意图。试验采用六分量天平测量螺旋桨的拉力和扭矩。数据采集器与六分量天平和计算机直接相连。电机固定在六分量天平上，天平则固定在由车厢伸出的撑杆上。试验来流速度范围约为0～50 km/h，功率范围约为0～300 W，海拔450 m。图10和图11为天平、数据采集器及车载试验的实物图。

将试验获得的离散点拟合为一条前进比曲线，使用时换算得到对应速度下的曲线。由于静止状态的转速曲线无法由前进比曲线换算得到，因此在进行静止状态对比时直接使用试验数据。图12为螺旋桨效率η和拉力系数CT试验离散点拟合示意图。

图9 螺旋桨车载试验系统示意图Fig.9 Schematic of vehicle testing system for propeller

图10 六分量天平(左)和数据采集器(右)Fig.10 Six-component balance (left) and data collector (right)

图11 车载试验实物图Fig.11 Ground vehicle test photos

2) 螺旋桨计算及结果分析

为了与商用CFD软件进行对比，本文同时使用Fluent对部分状态进行了计算。计算采用SSTk-ω湍流模型，基于结构-非结构混合网格，采用多重参考系方法进行计算。计算网格中，旋转域非结构网格量为95.598 1万，外部静止域结构化网格量为281.147 8万。计算状态选取：速度V0=0.406 3 m/s(静止状态计算收敛预设流速)，高度H=400 m，螺旋桨转速ns=1 000～5 000 r/min(接近试验状态)。图13为螺旋桨几何模型示意图。

在片条理论计算中，将0.2R内的部分作为桨毂(图13中深色部分)，不参与片条理论计算，桨叶等分为17段。但在CFD计算中则包含整个模型。

图12 JXF16×8试验数据示例Fig.12 Examples of JXF16×8 test data

图13 JXF16×8 螺旋桨几何模型Fig.13 Geometry model of JXF16×8 propeller

图14为静止状态下螺旋桨拉力、功率、力效的片条理论、CFD及试验曲线。图15为40 km/h前进速度下螺旋桨拉力和功率的片条理论及试验曲线。

在全状态下，CFD结果及修正的片条理论与试验结果较为吻合，片条理论的拉力及功率相对误差约在5%以内。出现误差的原因可能有以下几点：

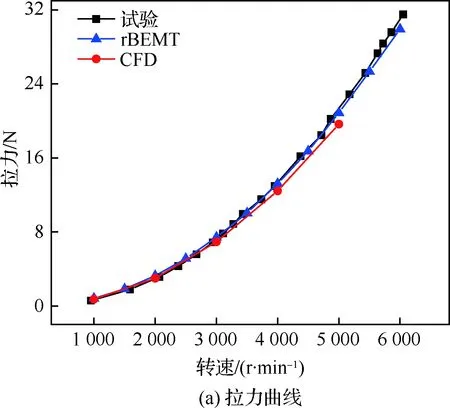
图14 静止状态JXF16×8螺旋桨特性曲线Fig.14 Performance curves of JXF16×8 propeller at 0 km/h

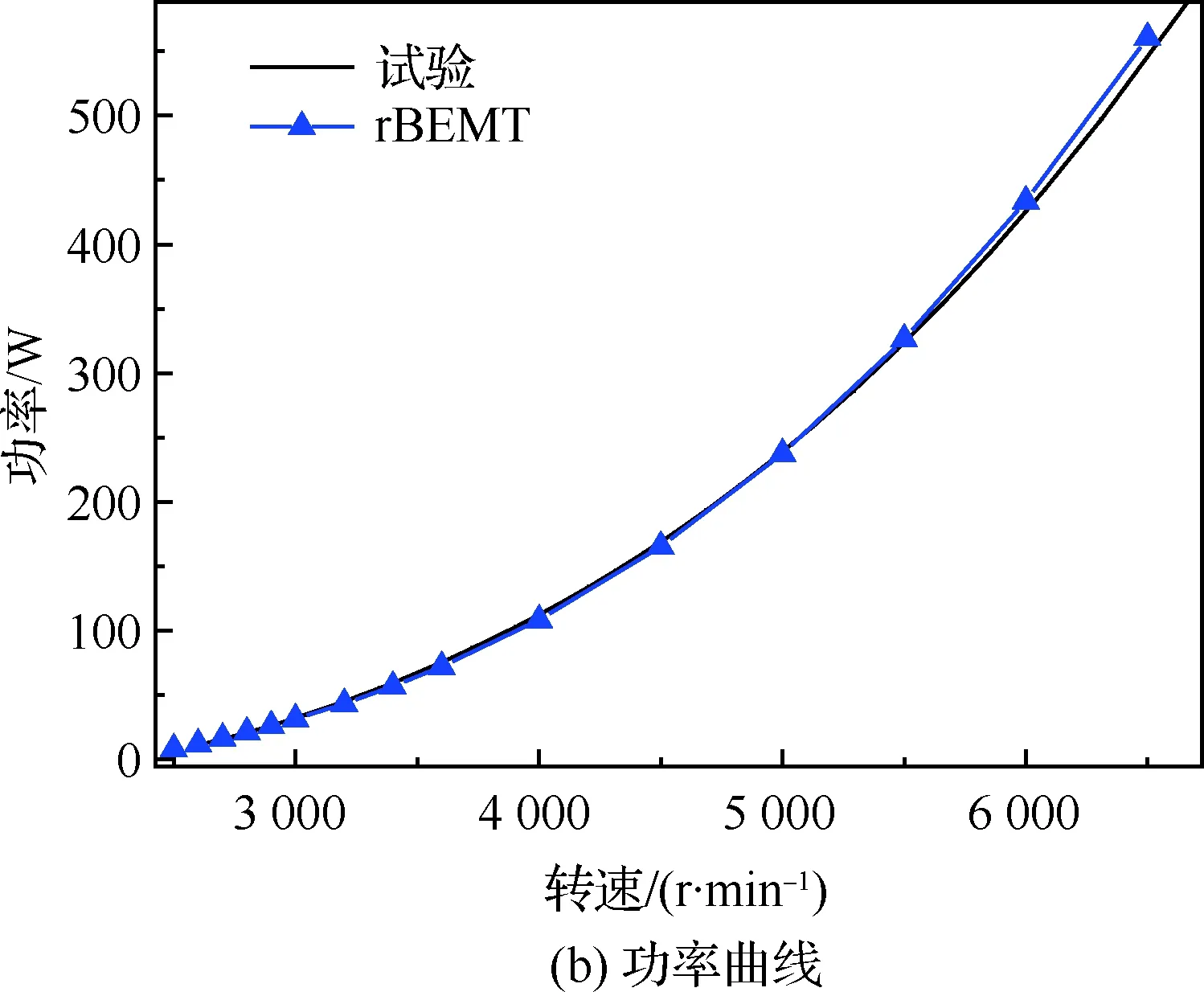
图15 40 km/h时的JXF16×8螺旋桨特性曲线Fig.15 Performance curves of JXF16×8 propeller at 40 km/h

1) 几何模型误差：螺旋桨桨尖形状和桨毂的建模与实物有一定差别，引起微小误差。

2) 片条理论中，仅有桨叶参与计算，桨毂产生的影响被忽略。在转速不大时，桨毂产生的阻力相对于桨叶拉力变大，因此片条理论在小转速时的预测结果偏乐观。

3) 试验状态的桨毂后面连接有支撑设备和仪器，而CFD桨毂部分后面是悬空状态，气流分离产生了较大的压阻，使得其计算结果较为保守。

为了进一步验证本文计算方法对不同高度及高前进比状态的计算仍然稳定且可靠，结合项目计算需求选取状态：高度500 m(12 m/s)、3 000 m(15 m/s)、10 000 m(20、33 m/s)及转速3 000、5 000、7 000 r/min，其他CFD计算条件与本节静止状态计算条件类似。CFD与rBEMT的计算对比结果如图16所示。

图16 JXF16×8螺旋桨不同高度下的拉力和功率Fig.16 Thrust and power of JXF16×8 propeller at different height

经过修正的片条理论结果与CFD的计算结果吻合较好，相对误差普遍低于5%。仅在10 000 m高度、33m/s状态下的计算偏离较大，这是由于在该状态下螺旋桨已经处于深度失速的风车状态，部分叶素处于-7°以下的负迎角状态，其气动数据是神经网络外插得到的，因此造成了一定误差。

3.2 其他螺旋桨模型算例

为了说明本文修正方法的几何无关性，本节选用特性不同的Falcon16×10碳纤维螺旋桨和流动状态差别较大的平直旋翼来验证本文的计算模型对不同螺旋桨模型具有同样的计算稳定性和准确性。

1) Falcon16×10螺旋桨算例

Falcon16×10碳纤维螺旋桨是一种著名的高效碳纤维螺旋桨商品，其车载试验方法与3.1节所述相同。计算状态为：前进速度V0=40 km/h，高度H=400 m，桨叶等分为17个截面，0.2R以内作为桨毂不参与计算。图17为片条理论与车载试验的拉力和功率曲线。

在n<6 500 r/min(桨盘载荷约为230 N/m2)时，计算结果仍然较为吻合，拉力相对误差保持在5%以内，功率相对误差在8%以内。

2) 静止状态旋翼算例

旋翼几何外形、工作状态、流动状态与螺旋桨有较大差异，构建一个直径D=1.5 m、弦长c=0.14 m、安装角i=7°、翼型为DAE-21的简单旋翼，0.2R以内不包含桨毂，如图18所示。计算状态为：来流速度V0=0.4 m/s，高度H=400 m。CFD湍流模型选为层流动能转捩(kkl)模型，其他计算条件与前文静止状态JXF16×8相似。

图19为片条理论与CFD计算拉力和功率曲线对比。由图可知，片条理论计算结果与CFD吻合良好，二者之间的拉力和功率相对误差均低于5%。