基于三次B样条曲线拟合的智能车轨迹跟踪算法

张永华，杜 煜，潘 峰，魏 岳

(1.北京联合大学 智慧城市学院，北京100101; 2.北京联合大学 机器人学院，北京100101;3.保定学院物理与电子工程系，河北保定071000)

(*通信作者电子邮箱duyu@buu.edu.cn)

0 引言

轨迹跟踪算法是智能车辆控制的一项关键技术，通过对车辆转向系统的控制，使车辆按照规划的行驶路线行驶，并满足一定的舒适性、安全性和稳定性，近年来国内外许多高校和科研院所对此都进行了广泛和深入的研究。以经典比例积分微分(Proportion-Integration-Differentiation，PID)控制理论为基础，早期研究人员由基于前方路径曲率的前馈控制和PID反馈控制器叠加组合的横向复合式控制系统，构建出非线性PID控制器［1］。以此为基础，研究人员又进一步提出了具有学习功能的自适应轨迹跟踪算法［2］和基于惯导航向角的非线性PID轨迹跟踪算法［3］。为了解决基于PID的轨迹跟踪算法的鲁棒性问题，研究人员提出了采用由期望方位偏差估计器和鲁棒PID反馈控制器组成的横向控制系统［4］和通过前轮主动转向和直接横摆力矩协调控制，实现了基于广义比例积分(Proportion-Integration，PI)控制的线性参变(Linear Parameter Varying，LPV)鲁棒增益调度控制器［5］。此外，基于横向位置误差和横摆率，研究人员提出了嵌套PID控制器［6］。PID控制器虽然可以处理智能车辆的轨迹跟踪问题，但由于其控制参数通过试凑法获取，因此难以实现对横向运动的最优控制。

除了基于PID控制理论的轨迹跟踪算法以外，针对车辆的运动学特性，提出了基于几何模型的轨迹跟踪算法。文献［7］提出了一种车辆侧滑约束下的满足车辆动力学特性的几何轨迹跟踪算法。而文献［8］结合模糊控制算法提出了一种改进的纯追踪控制算法。在此基础上，又进一步提出了在纯追踪控制算法中引入主动偏航控制的算法，从而实现了较高速度下稳定的轨迹跟踪［9］。

路径生成算法用于生成满足车辆动力学约束的平滑避障路径。文献［10］中将贝塞尔曲线用于纯追踪模型当中，实现了避免碰撞下的平滑路径的轨迹跟踪。文献［11］将贝塞尔曲线应用于具有回廊约束下的轨迹生成，通过轨迹的分段拼接生成具有C2光滑度的避障轨迹线。为了获取更加平滑的轨迹线，文献［12］中通过对四阶贝塞尔曲线的三个控制参数的最优化求解，从而得到满足车辆运动学约束和曲率连续约束的平滑轨迹线。更进一步地，文献［13］中提出了采用五次贝塞尔曲线分段拼接的方式来获取平滑路径。为了克服贝塞尔曲线需要分段拼接的问题，进一步提出了基于B样条的平滑路径生成算法。文献［14］将B样条曲线和反推控制器相结合，实现了满足车辆动力学约束下的平滑轨迹跟踪。此外文献［15］又进一步提出了根据前轮转向实现具有非线性约束的车辆转向控制。采用B样条曲线拟合的方式生成的平滑轨迹线，相比贝塞尔曲线，在相同阶次下，路径轨迹更加平滑，且改变个别控制点不会改变整条轨迹线，更有利于路径跟踪的平稳性［16］

为了应对多变的复杂实际驾驶场景，设计控制简单、易于调节、适应性和鲁棒性更强的轨迹跟踪算法，在现有几何轨迹跟踪算法［17］的基础之上，本文提出了一种实用的基于三次B样条曲线拟合的几何轨迹跟踪算法，使得拟合后的路径具有C2连续性，从而满足轨迹跟踪对平滑轨迹的要求，有利于高速下的稳定轨迹跟踪。该算法通过对先验地图中的离散轨迹点进行拟合，并通过拟合得到的轨迹方程重新生成带有切向角参数的离散路点，从而摆脱了现有几何轨迹跟踪算法在计算切向角时对高精度惯性导航设备的依赖。相比传统的基于PID的轨迹跟踪算法和现有几何轨迹跟踪算法，本文提出的算法不仅具有一定的轨迹优化能力，使得轨迹跟踪过程更加平稳;而且在有效避免了传统PID跟踪算法参数不易调节和现有几何跟踪算法对惯性导航设备依赖的问题的同时，能够适用于多传感器融合轨迹在较高速度下的轨迹跟踪，具有更好的适应性和跟踪精度。

1 理论基础

1.1 车辆运动学模型

在不考虑侧向滑动问题的前提下，汽车的运动学模型可以采用线性二自由度前轮转向模型来描述，如图1所示。

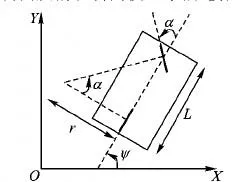
图1 前轮转向模型Fig.1 Front wheel steering model

车辆运动学模型如式(1)～(2)所示:

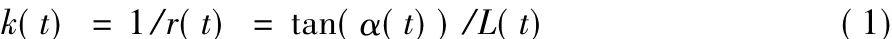
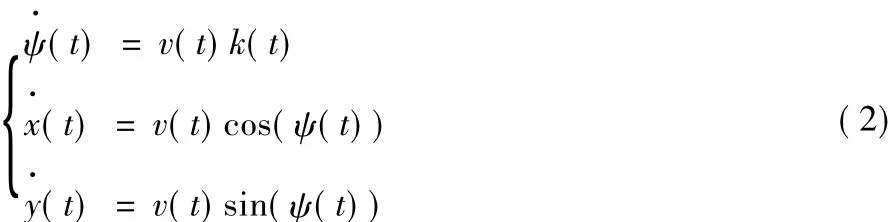
其中:(x，y)表示车辆的二维坐标;ψ表示航向角;k表示曲率;L表示前后轮轴距;r表示转弯半径;α表示前轮转向角;v表示车辆实时速度。

1.2 几何轨迹跟踪算法

本文采用和文献［17］相同的几何轨迹跟踪算法作为本文算法的基础理论部分。如图2所示，纵轴左侧曲线为先验地图轨迹线，(cx，cy)为到前轴中心点所在横轴与先验轨迹线相交的轨迹点。δ(t)为车轮实际转角，由横向偏差角θfa(t)和切向角θe(t)两部分构成，即:

其中横向偏差角θfa(t)是横向偏差efa(t)的非线性函数，即:

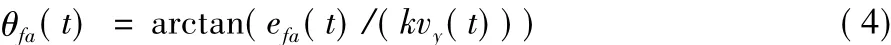
其中:横向偏差efa(t)是前轴中心点到轨迹点(cx，cy)之间的距离;vy(t)指的是车辆的实际行驶速度v(t)的纵向分量;k为增益参数;切向角θe(t)指的是轨迹点(cx，cy)的切线正方向与纵轴正方向的夹角。方向盘的转角φ(t)由车轮偏角和车轮转角到方向盘转角的映射函数μ(t)共同得到，即:

当增益参数k和纵向速度分量vy(t)为常数时，式(3)中横向偏差角θfa(t)在车轮实际转角δ(t)中所占的比重越小，表明轨迹跟踪的精度就越高，此时横向偏差efa(t)也就越小。因此可以用横向偏差efa(t)绝对值的大小来评估轨迹跟踪的效果。

式(4)中，在不同纵向速度分量vy(t)时，增益参数k用于调节横向偏差efa(t)对横向偏差角θfa(t)的贡献大小。当纵向速度由低到高逐渐增大时，为了保证智能车行驶过程中及时、平稳、安全地进行横向误差矫正，k值呈现非线性递增变化。

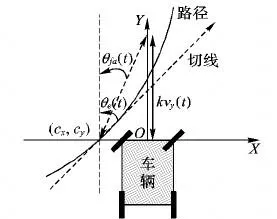
图2 几何轨迹跟踪算法示意图Fig.2 Schematic diagram of geometric path tracking algorithm

1.3 三次B样条曲线拟合原理

如图3 所示，设四个离散点为:P0、P1、P2、P3，其坐标分别为:(x0，y0)、(x1，y1)、(x2，y2)、(x3，y3); 设中点 M1=(P0+P2)/2、M2=(P1+P3)/2。要使拟合后的曲线起于始点P0，止于终点P3，需在起始端和终止端处分别增加一个点Ps=2P0－ P1和Pe=2P3－ P2，然后以新的点序列Ps、P0、P1、P2、P3、Pe为控制点绘制三次B样条曲线。

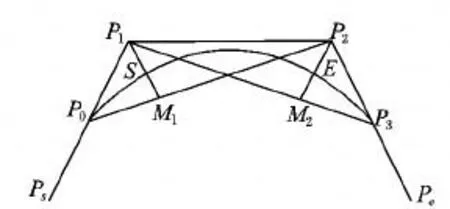
图3 三次B样条曲线拟合示意图Fig.3 Schematic diagram of cubic B-spline curve fitting

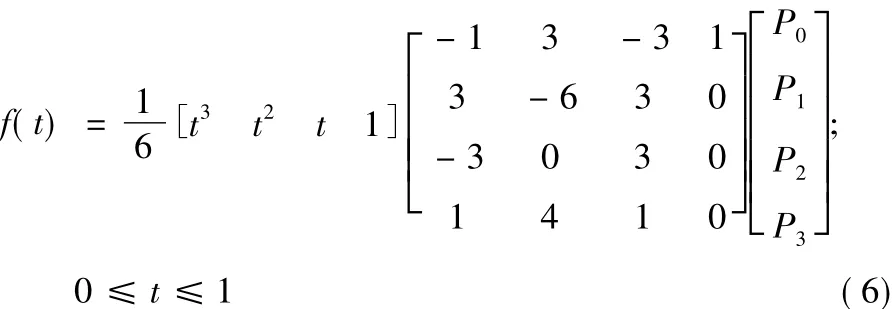
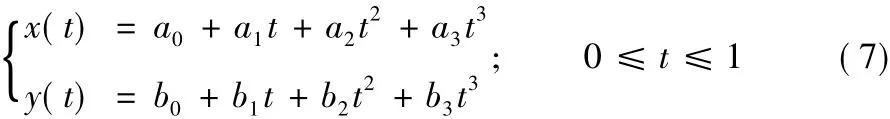
其中:

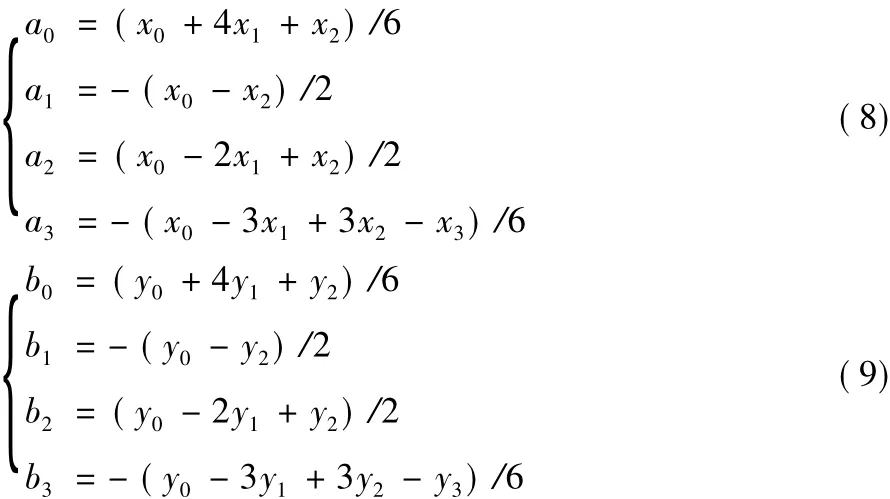
分量式为:

曲线的斜率为:

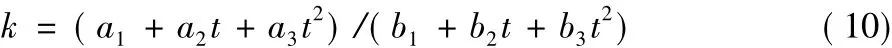
S点位于ΔP0P1P2的中线PM1上，距P1点P1M1/3处;E点位于ΔP0P1P2的中线P2M2上，距P2点P2M2/3处;S点切线平行于P0P2;E点切线平行于P1P3;拟合曲线以平均通过式的方式经过控制点。

当有 n个平面离散点时，记为 Pi(i=0，1，…，n －1)。以P0、P1、P2、P3绘制第1 条三次 B 样条曲线;以 P1、P2、P3、P4绘制第2条三次B样条曲线;以P2、P3、P4、P5绘制第3条三次B样条曲线;以此类推，以Pn－4、Pn－3、Pn－2、Pn－1绘制第n － 3 条三次B样条曲线。用该方法绘制的曲线自然衔接，具有C2级连续性。

1.4 轨迹点切向角获取算法

基于曲线拟合的切向角计算如式(11)所示:

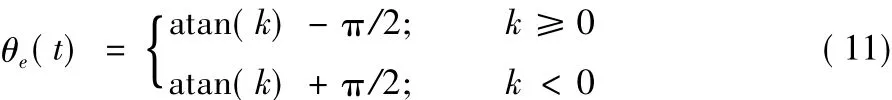
其中:k表示拟合轨迹线的斜率;atan(k)表示拟合轨迹线上的轨迹点的切线正方向与坐标横轴正方向的夹角。

轨迹点切向角获取算法流程如图4所示，主要分为如下步骤:

1)初始化参与拟合的离散轨迹点，并判断是否满足拟合条件，若满足条件则执行步骤2)，否则执行步骤4)。

2)循环计算前n－3个轨迹点的切向角。

3)计算最后三个轨迹点的切向角。

4)结束算法。

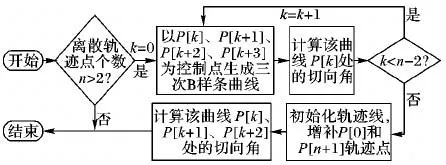
图4 轨迹点切向角获取算法流程Fig.4 Flow chart of path point tangential angle acquisition algorithm

2 实验平台

本文采用和文献［17］相同的实验平台和实验场地。如图5所示，该实验平台为北汽绅宝C70改装的智能车，其车头安装有一个LUX4激光雷达和一个毫米波雷达，用于检测车前远距离的动态和静态障碍物;车顶装有一个Velodyne64线激光雷达，用于检测车辆周围360°范围内的动态和静态障碍物;车尾有两个侧后方检测系统(Rear and Side Detection System，RSDS)毫米波雷达用于检测车辆左后和右后方向的动态车辆。该车还安装有组合导航系统一套，定位精度达到厘米级。车内安装两个同盟视觉科技派克(Allied Vision Technologies-PIKE，AVT-PIKE)相机，用于检测车道线、停止线、斑马线和红绿灯。

图5 北汽绅宝C70智能车实验平台Fig.5 Beiqi Saab C70 intelligent vehicle experimental platform

该智能车实验平台的车轮转角δ(t)取值范围为±33.7°。函数μ(δ(t))为车辆偏角到方向盘转角的传动比。由于汽车传动系统的限制，传动比函数是车轮偏角的非线性函数，因此，本文采用离散映射表的方式来近似逼近传动比函数。整个轨迹跟踪算法的最终输出为方向盘的转角φ(t)，取值范围为±540°。

实验路线如图6所示，实验地点选择在园博西二路、长顺三路、园博西一路和长顺二路组成的环形路线，各个路段分别用 L1、L2、L3和 L4表示，L1和 L2、L2 和 L3、L3 和 L4、L4 和L1之间的路口分别用C1、C2、C3、C4表示。实验路线中各个路段的信息和路口信息如表1～2所示。

由于实际场景中智能车的行驶速度和道路的曲率都在实时发生变化，因此根据不同的速度，选择一组合适的k值，对于轨迹跟踪的精确度和稳定性至关重要。本文经过实际道路的测试，得到了几何轨迹跟踪算法的k系数的离散映射值，速度为0 km/h～20 km/h、20 km/h～40 km/h、40 km/h～60 km/h的 k 值分别为 1/5、1/4.5、1/4.2。

由于考虑到算法实时性的要求，本文采用混合轨迹的方式来生成可行驶轨迹线，即车前30 m和车后10 m范围内采用三次B样条曲线分段拟合方式和六次贝塞尔曲线拟合方式生成具有切向角属性的平滑轨迹线，范围外的轨迹线仍然采用原始高精度地图轨迹线。通过采用这种策略，既能够保证轨迹跟踪对切向角的需要，同时又能够节约计算资源，提高系统的实时性。

图6 实验路线示意图Fig.6 Schematic diagram of experimental path

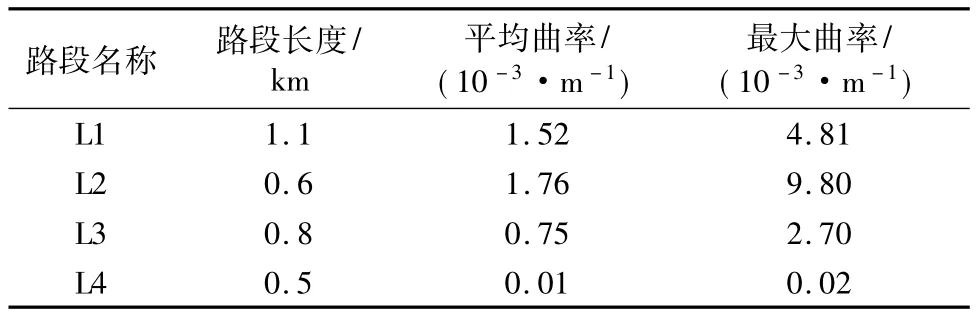
表1 实验路段信息Tab.1 Experimental road information

表2 实验路口信息Tab.2 Experimental crossroad information

3 实验结果及分析

测试实验分为轨迹拟合仿真实验和轨迹跟踪测试实验两个部分。第一部分，对三次B样条曲线拟合与文献［7］中采用的贝塞尔曲线拟合方法进行了轨迹拟合仿真实验，用于测试两种曲线拟合方法的特性，同时对两种拟合算法生成的路径采用基于线性二自由度的汽车模型进行了轨迹跟踪仿真实验，用于测试其跟踪效果。第二部分进行了真实车辆平台的轨迹跟踪测试实验，并与文献［3］中提出的基于航向角的轨迹跟踪算法和文献［7］中提出的基于贝塞尔曲线拟合的轨迹跟踪算法进行了对比实验。根据实验路段的特点，该部分实验分为两个子实验。首先对由L1、L2、L3和L4组成的环形实验路线进行了20 km/h绕圈轨迹跟踪测试实验，用于测试算法在低速时不同曲率道路下的跟踪效果。然后以L1实验路段为测试路段，进行了60 km/h直道轨迹跟踪测试实验，用于测试算法在较高速度小曲率道路下的跟踪效果。

3.1 轨迹拟合仿真实验

3.1.1 轨迹拟合特性仿真

如图7所示，三次B样条曲线具有很好的平滑性，而且相比六次贝塞尔曲线，拟合结果更接近原始轨迹线，在实际的路径规划中，尤其是对于曲率变化比较大的轨迹线，拟合效果整体优于高阶贝塞尔曲线。另一方面，对于n点曲线拟合来说，采用三次B样条曲线拟合时，整条轨迹线的阶次保持不变，此外当若干个轨迹点发生变化时，只有拟合轨迹线的局部位置发生变化，拟合算法的稳定性和计算复杂性都较低。而当使用贝塞尔曲线进行拟合时，对于n个轨迹点，需要n－1次贝塞尔曲线，而且当若干个轨迹点发生变化时，整条拟合轨迹线都会发生变化，拟合算法的稳定性和计算复杂性相比三次B样条曲线拟合都较差。

3.1.2 轨迹跟踪仿真实验

基于车辆运动学模型，对三次B样条曲线和六次贝塞尔曲线进行轨迹跟踪仿真实验，实验结果如图8所示。当原始轨迹线是一个曲率急剧变化的三角波路径时，采用三次B样条曲线进行轨迹拟合时，平均跟踪误差为3.05 m，最大跟踪误差为7.62 m;而采用六次贝塞尔曲线进行轨迹拟合时，平均跟踪误差为5.27 m，最大跟踪误差为11.98 m。采用六次贝塞尔曲线拟合相比采用三次B样条曲线拟合，其平均跟踪误差要高出72.79%，最大跟踪误差高出57.22%，实验结果表明采用基于三次B样条曲线拟合的轨迹跟踪算法在轨迹曲率变化较大的情况下跟踪效果优于基于贝塞尔曲线拟合的轨迹跟踪算法。

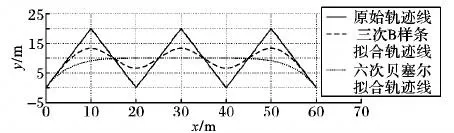
图7 曲线拟合仿真示意图Fig.7 Schematic diagram of curve fitting simulation

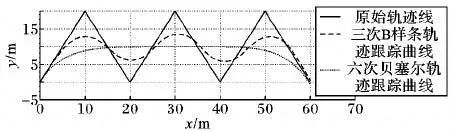
图8 轨迹跟踪仿真示意图Fig.8 Schematic diagram of path tracking simulation

3.2 轨迹跟踪测试实验

3.2.1 20 km/h环形路线轨迹跟踪测试

如图9(a)、(b)所示，三种轨迹跟踪方式的切向角曲线和方向盘转角曲线整体上都具有很好的连续性和平滑性。其中基于航向角的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.15°和5.00°以内的局部微小震荡。基于三次B样条曲线拟合的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.11°和3.80°以内的局部微小震荡;基于六次贝塞尔曲线拟合的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.09°和3.20°以内的局部微小震荡。实验表明智能车在低速时不同道路曲率下行驶时三种轨迹跟踪方式跟踪的平稳性良好。如图9(c)所示，基于航向角的轨迹跟踪算法、基于三次B样条的轨迹跟踪算法和基于六次贝塞尔曲线拟合的轨迹跟踪算法的跟踪误差的绝对值的平均值分别为0.029 m、0.034 m和0.065 m，最小跟踪误差为都为零，最大轨迹跟踪误差分别为0.30 m、0.30 m和0.50 m。实验表明低速时当轨迹线的曲率变化较大时，基于三次B样条曲线拟合的轨迹跟踪算法相比基于航向角方式的轨迹跟踪算法跟踪精度差异不大，都具有较好的跟踪精度，而相比基于六次贝塞尔曲线拟合的轨迹跟踪算法在跟踪精度方面则具有明显的优势。实验表明三次B样条曲线拟合得到的平滑轨迹线相比六次贝塞尔曲线拟合得到的平滑轨迹线与原先验轨迹线的贴合程度更好。

图9 20 km/h环形路线轨迹跟踪测试数据分析图Fig.9 Data analysis diagram of path tracking test for ring path at 20 km/h

3.2.2 60 km/h 直道轨迹跟踪测试

如图10(a)、(b)所示:基于航向角的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.23°和4.80°以内的局部微小震荡;基于三次B样条曲线拟合的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.20°和3.80°以内的局部微小震荡;基于六次贝塞尔曲线拟合的轨迹跟踪算法的切向角曲线θe(t)和方向盘转角曲线φ(t)分别存在0.25°和4.20°以内的局部微小震荡。实验表明在较高速度时智能车在小曲率道路下三种轨迹跟踪方式跟踪的平稳性良好。如图10(c)所示，基于航向角的轨迹跟踪算法、基于三次B样条的轨迹跟踪算法和基于六次贝塞尔曲线拟合的轨迹跟踪算法的跟踪误差的绝对值的平均值分别为0.186 m、0.231 m 和0.338 m，最小跟踪误差为都为 0.1 m，最大轨迹跟踪误差分别为0.30 m、0.30 m 和0.40 m。实验表明:较高速度下进行小曲率轨迹跟踪时，基于三次B样条曲线拟合的轨迹跟踪算法和基于航向角方式的轨迹跟踪算法跟踪精度差异不大，都具有很好的跟踪精度，而相比基于六次贝塞尔曲线拟合的轨迹跟踪算法跟踪精度方面则略有优势。

图10 60 km/h直道轨迹跟踪测试数据分析图Fig.10 Data analysis diagram of path tracking test for straight path at 60 km/h

实验表明:基于三次B样条曲线拟合的轨迹跟踪算法在低速大曲率和较高速度小曲率时，相比基于航向角方式的轨迹跟踪算法跟踪效果差异不大;但是，相比基于航向角方式的轨迹跟踪算法，该算法解除了对高精度惯导设备的依赖，实现了基于不同传感器轨迹跟踪算法的统一。实验还表明，在低速大曲率时，本文提出的算法相比基于六次贝塞尔曲线拟合的轨迹跟踪算法具有明显的优势，在较高速度小曲率时也有一定的优势，总体上本文提出的基于三次B样条曲线拟合的轨迹跟踪算法优于基于六次贝塞尔曲线拟合的轨迹跟踪算法。

4 结语

本文介绍了基于三次B样条曲线拟合方式的几何轨迹跟踪算法。与传统的基于惯导航向角的轨迹跟踪算法和基于六次贝塞尔曲线拟合的轨迹跟踪算法相比，本文算法具有如下优点:该算法在不损失轨迹跟踪性能的前提下，摆脱了对高精度惯导设备的依赖，降低了研发成本;由于该算法的切向角不依赖硬件设备，因此该算法能够实现多传感器融合的路径跟踪;该算法能够对行驶轨迹进行平滑处理，具有一定的轨迹优化能力。

采用了本文算法的智能车驾驶平台参加了2016年中国智能车未来挑战赛，在简单的城市环境下以最高40 km/h和简单高速环境下以最高60 km/h的速度顺利完成比赛，并取得了较好名次。比赛结果充分证明了该算法的适应性和准确性。但是，针对本算法的验证测试还不够充分，需要开展更多的、更广泛的测试实验来进一步验证算法的适应性和准确性。