脉冲神经元脉冲序列学习方法综述

徐 彦，熊迎军，杨 静

(1.南京农业大学信息科技学院，南京210095; 2.北京师范大学珠海分校管理学院，广东珠海519087)

(*通信作者电子邮箱xuyannn@njau.edu.cn)

0 引言

脉冲神经网络被称为第三代神经网络［1］，其以更接近真实神经元的方式运行，具有强于传统神经网络的性能［2］。脉冲神经元以脉冲激发时间作为输入和输出，可以更好地模拟生物神经元进而可以成为更有效模拟人工智能的基础。

在人工神经网络的研究中，有监督学习理论一直属于核心研究内容。由于人脑神经系统中神经元激发的脉冲序列为各种认知活动的生理基础［3］，因此脉冲神经元与网络的有监督学习具有重要的应用价值，成为其研究领域中一个极重要的组成部分。而这其中，以脉冲的激发时间编码的有监督学习又成为研究者重点关注的研究方向。

基于时间编码的脉冲神经网络有监督学习方法按照激发的脉冲个数可以大致分为单脉冲学习(如Tempotron［4］)和多脉冲学习方法两类。很显然，多脉冲学习更加符合生物神经元运行的特征并且也具有更强的应用性能。如果按照适用的网络结构可以把脉冲神经网络有监督学习方法分为单神经元学习和网络学习方法两类。已有有监督学习方法在网络结构和脉冲个数上的一个普遍规律是单神经元学习方法的多脉冲学习能力普遍较强，可以通过学习控制更多的脉冲激发时刻，而多层网络的学习方法一般只控制较少的输出脉冲个数。

这里先介绍几个概念的定义。脉冲神经网络的有监督学习是指通过学习使得输出神经元激发出一串特定的期望输出脉冲序列。基于时间编码的脉冲神经网络有监督学习是指在一段运行时间内通过学习使得输出神经元精确地在指定的时刻激发出脉冲。基于时间编码的单脉冲神经元的多脉冲有监督学习(以下简称单神经元学习)是指具有多个输入突触的单个脉冲神经元通过学习在期望的时刻激发出多个脉冲，即脉冲序列，所以本文又称之为脉冲序列学习。

脉冲神经元是构成脉冲神经网络的基本单元，单脉冲神经元的有监督学习可以更好地借鉴已明确的生物神经元突触调整机制，同时是实现更复杂神经网络有监督学习的基础［5］，因此具有重要的意义。单神经元脉冲序列学习的过程受到诸多因素的影响，包括输入输出脉冲序列长度、激发率，神经元突触个数等。序列越长、激发率越高会导致学习的难度越大;但是，诸多的因素也使得脉冲序列学习具有更加灵活的权值调整可用信息。

目前，已有不同的研究者提出了若干单神经元学习方法。其中，有一类是基于随机模型提出的［6－7］，这类非确定性方法难以分析比较它们对复杂目标序列的学习能力。文献［8］利用线性代数的方法给出了一种脉冲序列学习方法，但是这种方法的理论脱离脉冲神经元的特点过多，因此较少被研究者关注。另外，也已经有综述性的文献介绍脉冲神经网络的学习方法［9－10］，但是这些研究的介绍都比较广泛，没有特别针对脉冲序列学习方法，或者没有进行实验比较不同方法的序列学习能力。序列学习能力是脉冲序列学习方法的核心性能，同时对于越长越复杂脉冲序列学习能力越强的方法将具有更强的应用能力，也更能体现脉冲神经元的特征。

本文以确定性的学习方法为对象，较详细地介绍了几种目前主要的脉冲序列学习方法，这些方法基于不同的理论依据，具有不同的权值调整方式，在性能上存在较大的差别。本文通过实验比较了这几种方法的学习性能，分析和总结了它们的特点。

1 脉冲神经元模型

目前，存在多种脉冲神经元模型，这些模型大多从生物神经元内部物理化学活动的规律抽象出模型表达式，这其中，集成激发模型(Leaky Integrate-and-Fire model，LIF)［11］与脉冲反应模型(Spike Response Model，SRM)［12］是脉冲序列学习方法研究中最常见的模型对象。

LIF是最基本、也是最常被研究的一种阈值 激发模型，这个模型基于生物神经元在生物电子学上表现出的一些特征。一个通过突触在时刻t(g)输入的脉冲经过一个低通滤波器，这个低通滤波器将脉冲形式的短暂脉冲转换成一个电流脉冲I(g)(t)。这个电流脉冲会升高神经元内部电路的电压，升高的电压可以看成是神经元的突触后膜电位值的改变量。神经元内部电路中并联着一个电阻Rm和一个电容C。一旦在神经元内部电容上的电压超过激发阈值，神经元会激发出一个脉冲。根据电路中电流、电压和电容的相互关系，这个模型的神经元膜电位u随着时间的表达式为:

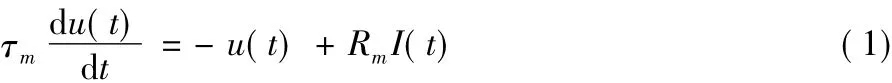
其中τm=RmC，称为膜时间常数。一个具体的LIF神经元由电流I(t)决定，I(t)为沿着所有突触到达神经元的输入脉冲在神经元内部形成的电流脉冲并且在突触强度影响下的总和，即:

其中:N是神经元输入突触个数;wi是神经元第i个突触的权值;Ii(t)是第i条突触所有输入脉冲引起的电流脉冲的总和，而每一个输入脉冲通过一个核函数转换为电流脉冲。因此，有:

其中:H(t)是Heaviside阶跃函数;K(t)为核函数。

LIF的表达式是微分方程形式，而SRM则具有直观的表达式，一种通用的SRM神经元的膜电位表达式为:

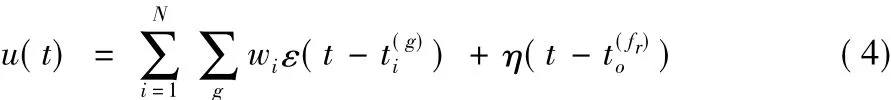
一个输入脉冲产生的突触后电位(PostSynaptic Potential，PSP)，由反应函数ε(t)决定。当神经元的膜电位由低到高超过神经元的激发阈值，神经元会在这个时刻激发出一个脉冲(这里用表示)，随后神经元进入绝对不应期和相对不应期，这两个过程会对神经元在后面时间的内部状态和脉冲激发产生影响。膜电位表达式中加入不应期函数η(t－)描述相对不应期的影响，为当前时刻之前的最靠近当前时刻的脉冲激发时刻。

不同的脉冲神经元模型之间并不独立，通过求解微分方程的通解可以得到LIF一个确定性的表达式［12］，而这个表达式可以看成是一种SRM。

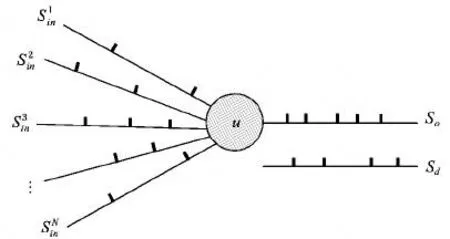
图1 脉冲序列学习Fig.1 Spike sequence learning

在神经元运行过程中实际激发脉冲的时刻记为To={，…，}，期望输出脉冲的时刻记为Td=，，…}，沿着第i个突触输入神经元的脉冲的到达时刻记为={，…};则实际输出脉冲序列可以记期望输出脉冲序列可以记为

2 脉冲序列学习方法

2.1 基于梯度下降的方法

基于梯度下降的脉冲反向传播(Spike Back Propagation，SpikeProp)方法［13］是最早出现的脉冲神经网络有监督学习方法之一，这个方法将著名的BP(Back Propagation)算法推广到脉冲神经网络。在SpikeProp的研究基础上，带动量的反向传 播、QuickProp(Quick Back Propagation)、Levenberg-Marquardt BP等提高学习性能的反向传播算法被应用到脉冲神经网络上［14–16］。这几种方法所采用的是纯粹的单脉冲结构，即输入、隐层、输出神经元都被限制仅仅激发一个脉冲或者仅仅控制一个脉冲的激发时间。文献［17］首先提出了一种基于多脉冲激发的反向传播学习模型，但是这个方法中仅仅是隐层神经元可以激发多脉冲，而输出神经元只能通过学习控制第一个脉冲的激发时间，所以仍然属于单脉冲学习模型。类似的，文献［18］提出了一个多脉冲输出网络结构，称之为MuSpiNN(Multi-Spiking Neural Network)网络模型，以及这个模型上的多脉冲输出反向传播学习算法Multi-SpikeProp，但是这个模型的多脉冲特性同样仅仅体现在隐层神经元上，作为构建误差函数的输出神经元同样只能为单脉冲输出。

文献［19］通过构造多脉冲情形下的误差函数实现了基于梯度下降的脉冲序列学习方法。基于梯度下降的方法需要构造误差函数，脉冲序列学习中误差函数由期望输出和实际输出脉冲序列构成。文献［19］中的方法当神经元运行完成得到完整的实际输出脉冲序列后再与期望输出脉冲序列构成误差函数，其权值调整是在神经元运行完成后进行，因此属于离线学习方式。

由生物学研究可知，生物神经元大多数情况下是在有脉冲激发时按照一定的机制立刻调整突触强度，也就是属于在线调整。在线方式的脉冲神经元有监督学习方法更符合生物学基础，而且预期也会有更强的学习性能，因此在理论研究和实际应用上都有一定优势。在线的脉冲序列学习方法在神经元运行过程中一旦有脉冲激发就立刻调整突触权值。文献［20－21］提出了在线的基于梯度下降的脉冲序列学习方法(Online Gradient-Descent-Based Multi-Spike，OnMSGDB)。这个方法基于SRM神经元提出，并且在神经元有脉冲激发时立刻根据当前激发脉冲和对应的期望输出脉冲构造实时误差函数。具体的，设当前激发的为第f个实际输出脉冲，第 f个期望输出脉冲为，则由这两个脉冲构建的误差函数定义如下:

接着就是利用梯度下降法最小化这个误差函数得到权值调整公式，即:

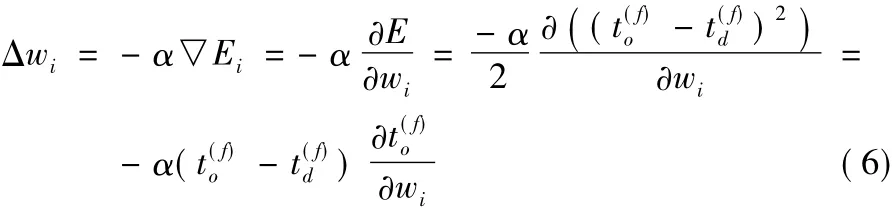
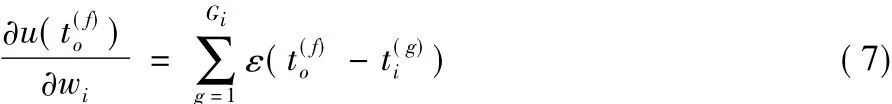
2.2 ReSuMe方法

基于梯度下降的方法是传统神经网络研究中常用的方法，另一种传统神经元常用的权值调整方法是Widrow-Hoff规则。这个规则目前也成为几种脉冲神经元脉冲序列学习方法的理论基础。标准的Widrow-Hoff规则表达式为:

其中xin、yd、yo分别代表神经元的输入、期望输出与实际输出。由此表达式可知Widrow-Hoff规则中神经元依据实际与期望输出之差并且乘以输入计算调整权值。

Widrow-Hoff规则只能处理实数形式的输入输出，因此不能直接应用于脉冲神经元。因为脉冲神经元与真实生物神经元的密切联系，其学习方法可以借鉴生物神经元的突触调整机制，例如依赖时间的突触可塑性(Spike-Timing-Dependent-Plasticity， STDP)［22］规 则。 ReSuMe(Remote Supervised Method)方法［23］使用窗口函数首次克服了Widrow-Hoff规则的限制并且结合STDP规则实现脉冲序列学习，其权值调整表达式为:

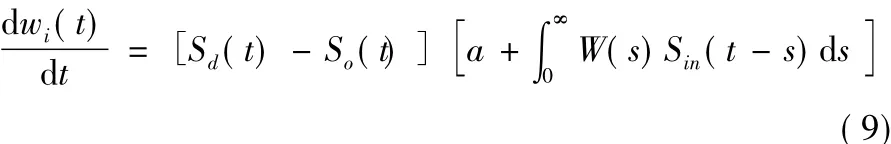
其中:a是一个权值更新的常数，表示一个恒定不变的更新量;W(s)称为学习窗口函数，它将离散的输入脉冲的时刻转换成Widrow-Hoff规则可以处理的形式。由式(9)可知权值更新幅度由输入脉冲与实际输出脉冲或者期望输出脉冲之间的时间间隔根据窗口函数计算而得。

在式(9)中，Sd(t)－So(t)在形式上表示期望与实际输出的差别，但是如果将输入脉冲序列与输出脉冲序列分别考虑，ReSuMe方法的权值更新实际上可以分为两部分。第一部分是权值的增强:当神经元运行时遇到任何一个期望输出脉冲所在的时间点，就要在这个时间点根据输入脉冲的时刻计算增强突触权值;第二部分是权值的减弱:当神经元在运行过程中一旦激发出脉冲，就要在这个实际输出脉冲的时间点根据输入脉冲的时刻计算减弱突触权值。由于ReSuMe的窗口函数独立于神经元的内部状态表达式，因此其可以适用于多种神经元模型，并且具有较好的综合性能。在标准ReSuMe方法的基础上，不少研究者对其进行了推广，例如在算法中加入时间延迟［24］。

2.3 脉冲模式联想神经元方法

文献［25－26］提出了一种称为脉冲模式联想神经元(Spike Pattern Assoiation Neuron，SPAN)的学习方法，这个方法也是基于Widrow-Hoff规则。SPAN方法采用卷积方式将离散的脉冲输入与输出时刻转换为实数形式，其首先用一个卷积核函数(t)作用于输入、期望与实际输出脉冲序列，即:

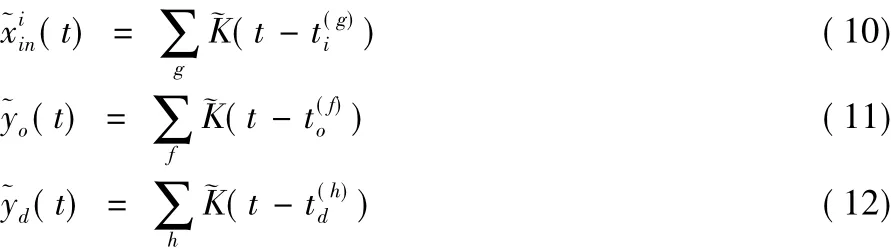
卷积之后得到每一个输入或输出脉冲激发时刻在时刻t对应的实数值。接着将卷积后得到的(t)(t)代入Widrow-Hoff规则得到权值调整公式的连续形式为:

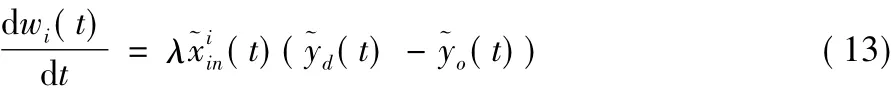
因此有:

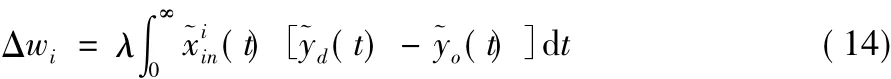
其中λ是学习速率。SPAN方法可以采用多种不同的卷积核函数，这增加了它的灵活性。

2.4 精确脉冲驱动突触调整方法

文献［27］提出了一种称为精确脉冲驱动突触调整(Precise-Spike-Driven synaptic plasticity，PSD)的方法，该方法基于LIF神经元模型提出，也是采用卷积方式将脉冲的时间转换为实数以采用Widrow-Hoff规则调整权值。与SPAN方法不同的是PSD方法只对输入脉冲进行卷积，而且由于采用与神经元表达式(3)中相同的卷积核函数K(t)，因此PSD实际上是依据神经元的输入电流大小调整权值。其权值调整表达式为:

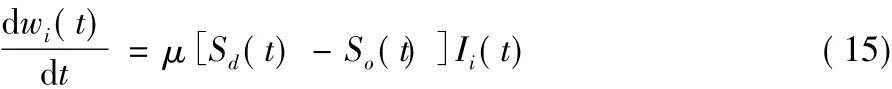
因此:

其中Ii(t)如式(3)所示，表示神经元内部由输入脉冲引起的电流大小，这个电流与神经元内部膜电位的变化直接相关，因此PSD方法的权值调整计算公式与LIF神经元的内部状态密切相关。式(16)右端的两部分表明PSD方法的运行方式类似于ReSuMe方法，即在期望输出脉冲处增强权值，在实际输出脉冲处减弱权值。

2.5 有限精度方法

文献［28］中较详细地讨论了脉冲神经元的的有监督学习问题，包括一个神经元存储输入输出模式的能力以及学习脉冲序列的能力等。文献［28］提出了一种可以实现脉冲序列学习的有限精度(Finite Precision，FP)算法，并且对脉冲的激发提出了时间容错的概念，即在学习时并不要求精确地在期望输出时刻激发脉冲，而是在期望输出时刻的一个时间邻域内激发即可。基于容错的概念，FP算法当期望输出脉冲时刻的邻域内没有脉冲激发，则增强权值;如果在邻域外有脉冲激发或者在邻域内有多于一个脉冲激发则减弱权值，其权值调整的具体规则与ReSuMe类似。

2.6 非线性脉冲序列核方法

文献［29］提出了一种称为非线性脉冲序列核(nonlinear Spike Train Kernels，nSTK)的学习方法，这个方法也是基于Widrow-Hoff规则。nSTK将一个卷积核作用于输入脉冲序列，与PSD不同的是可以选择多种核函数并且增加一个非线性函数与卷积核一起完成对输入脉冲序列的转换。其权值更新规则为:

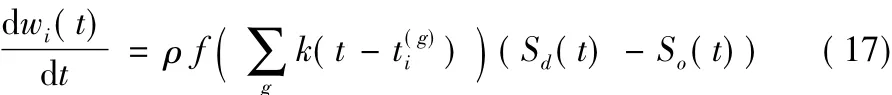
其中:ρ为学习速率;k(t)是卷积核函数;f(x)为非线性函数，这个非线性函数通常可以选择tanh(x/ζ)或者(1－e－x/ζ)。

2.7 Chronotron方法

文献［30］提出一种名为Chronotron的方法。Chronotron方法有两种学习机制:E-learning和 I-learning。其中，E-learning机制也是基于梯度下降的思想，通过梯度下降缩小实际输出脉冲序列与期望输出脉冲序列之间的差别。与OnMSGDB不同的是E-learning机制采用VP(Victor-Purpura)距离［31］来度量两种输出脉冲之间的差别。

VP距离依据从实际输出脉冲序列转换为期望输出脉冲序列所需要的最小代价来度量两种序列的距离。这个转换包含三种操作:在实际激发脉冲序列中增加期望的输出脉冲、删除不期望的并且在上次学习中没有移动的输出脉冲、移动某一个脉冲的激发时间到达对应的期望输出脉冲的时间。基于VP距离的期望与实际输出脉冲序列的误差函数表达式为:

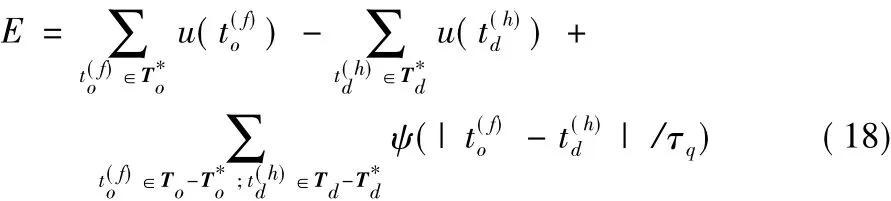
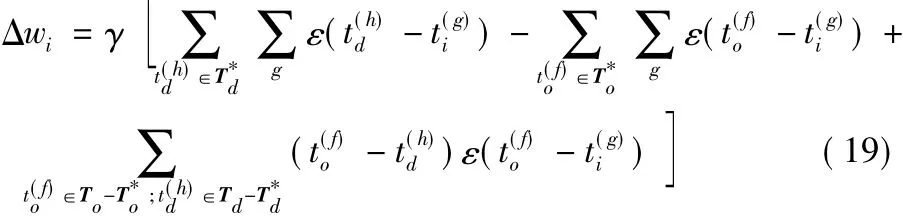
Chronotron的第二种学习机制称为I-learning。I-learning基于LIF神经元提出，一个突触的权值依据沿着这个突触到达神经元的脉冲引起的带权值电流进行调整，具体规则为:

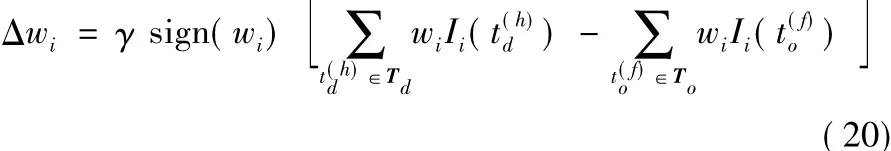
其中:γ是学习速率;wiIi表示带权值的电流;sign(wi)是权值wi的符号。由式(20)可知，I-learning在期望输出脉冲的时刻增强权值，在实际输出脉冲的激发时刻减弱权值，这一运行机制也与ReSuMe方法的运行机制类似。

2.8 滤镜误差方法

文献［32］提出了一种脉冲序列学习方法称为滤镜误差(FILTered-error，FILT)。这种方法基于随机的学习模型提出，但是最终被转化为确定性的学习方法，从而克服了随机模型不利于实现精确脉冲激发时间控制的缺陷。FILT方法将期望与实际输出脉冲之间的误差先用一个滤镜函数作用，然后调整权值减少这种滤镜作用后的误差。其权值调整公式为:

其中λ是学习速率。由于引入了滤镜函数，使得FILT没有直接采用PSP或者神经元突触电流作为权值调整公式，其权值计算函数σ(x)与其他学习方法的权值计算函数最大的区别是当输入脉冲的时间晚于当前调整权值的输出脉冲时刻时，依然会有效地调整权值，因此FILT更符合生物神经元突触前与突触后脉冲都会影响突触强度的生理机制。

2.9 基于感知机规则的脉冲序列学习方法

文献［33］提出了一种基于感知机规则的脉冲序列学习方法(Perceptron Based Spiking Neuron Learning Rule，PBSNLR)。感知机是以硬极限函数作为激活函数的最简单的传统人工神经元，其学习方法感知机规则是最简单的传统神经元学习方法。感知机通过神经元的输出是1还是0来实现简单的样本分类，而其权值W的调整根据期望输出d与实际输出a之间的差别进行，具体规则为:

其中:p是样本输入;Wold和Wnew分别表示调整前与调整后的权值。

PBSNLR将脉冲神经元的运行时间分为有脉冲激发与无脉冲激发两类，从而将其有监督学习转换为两分类问题，然后使用感知机规则来解决这个分类问题。PBSNLR以SRM神经元模型为对象，首先在神经元运行时间上的任一时刻珋t处得到用于感知机规则学习的样本输入，这个样本输入直接由神经元内部膜电位表达式(4)去掉权值wi计算得到。对应于第i个输入突触的样本输入的分量为:

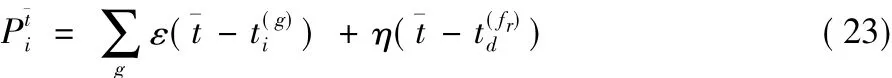
在目前已有的脉冲序列学习方法中，PBSNLR、E-learning是离线学习方法;OnMSGDB、ReSuMe、PSD、SPAN、FP、nSTK、I-learning和FILT可以以在线方式运行。同时在基本的学习方法的基础上，也有研究者从脉冲神经元本身的特点出发研究提高脉冲序列学习方法性能的通用方法。例如，选择适当个数的输入脉冲进行权值更新计算［36］，或者采用带噪声的激发阈值［37］等。

3 性能比较与分析

3.1 各种方法的脉冲序列学习性能比较

不同脉冲序列学习方法的理论基础或者具体的权值调整规则各不相同，因此它们的性能肯定存在差异。衡量一个学习方法脉冲序列学习能力的性能指标通常为学习精度与效率。下面进行两组实验考察上述几种脉冲序列学习方法的性能。

在这几种学习方法中，PSD、SPAN、I-learning都是基于LIF神经元模型提出，而ReSuMe方法和nSTK方法可以适用于不同的神经元模型，OnMSGDB、PBSNLR、E-learning和FILT基于SRM模型提出。因为LIF模型可以转换为SRM模型，所以我们选择在LIF神经元上运行实验。另外因为FP方法的权值调整规则与ReSuMe类似，同时其特有的容错区间使其不适合与其他方法直接比较性能，因此本文的实验中不考虑FP方法。实验中LIF神经元的卷积核函数取为:

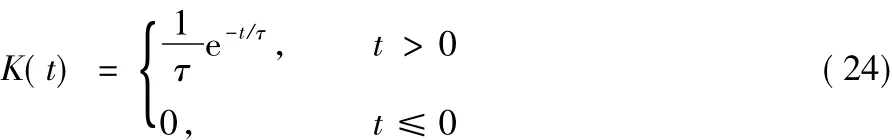
其中τ是一个常数。此时，通过解微分方程得到的对应SRM模型的表达式为:

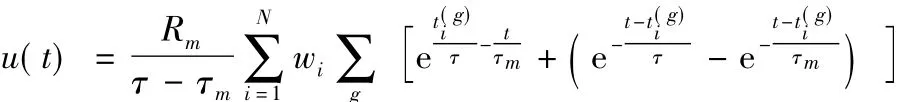
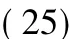
因为ReSuMe方法的窗口函数选择并不唯一，本文中采用如下形式的窗口函数:

其中:A是一个常数;τ+是决定学习窗口函数性态的时间延迟常数。

SPAN方法的卷积核函数选择与文献［13］中相同的形式，即:

对于nSTK方法，采用和PSD方法相同的核函数，即神经元表达式中转换电流的核函数 K(t)，非线性函数选择tanh(x/ζ)。FILT方法的权值调整函数取和文献［32］相同的形式，即:

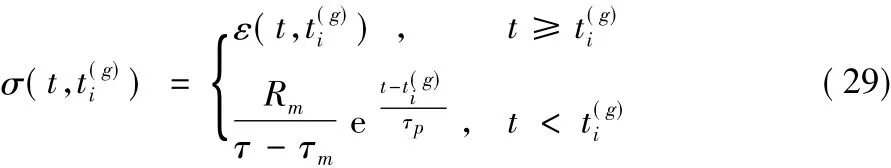
实验中神经元与学习方法的相关参数设置如表1所示。

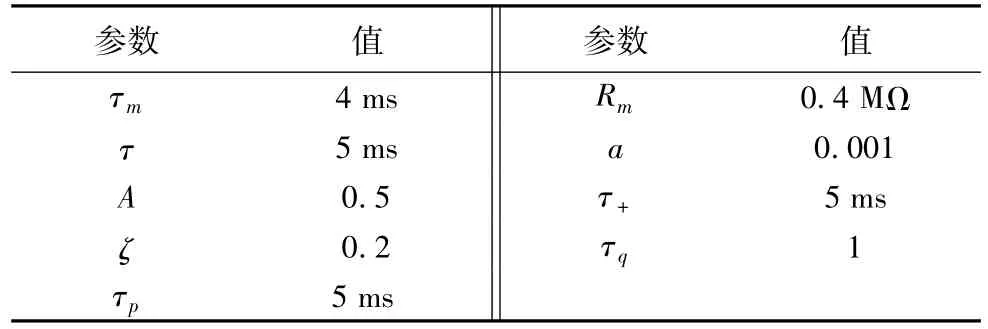
表1 神经元与学习方法的参数Tab.1 Parameters of spiking neurons and learning methods

在脉冲序列学习中，评价学习结果的好坏就是判断神经元在学习结束后实际激发的脉冲序列与期望输出脉冲序列接近的程度，这实际上就是度量两个脉冲序列之间的距离。本文采用基于相关性的度量C［38］来描述这个距离。C的值在区间［0，1］内，如果学习结束后根据实际与期望输出脉冲序列计算得到的C值越接近1，则说明两个序列越接近，即学习精度越高，越接近0则精度越低。因为采用计算机编程模拟神经元运行，因此需要将连续的运行时间离散化，本文中离散精度设置为1 ms。

在第一组实验中，一个含有400个突触的LIF神经元学习输出1600 ms的脉冲序列。输入与输出脉冲序列分别为激发率为10 Hz和100 Hz的Poisson序列。神经元的初始权值取区间(0，1.2·10－3)上的均匀分布。各方法的学习速率设定如下:OnMSGDB(On)和 E-learning(E-l)为 0.01;PSD(PS)、PBSNRL(PB)和 ReSuMe(Re)为 0.2;nSTK(nS)、SPAN(SP)、I-learning(I-l)和FILT(FI)为0.1。每种方法进行50次实验，实验中最大的学习周期数设定为5000步，实验后计算每种方法最高学习精度的平均值以及达到最高精度需要的学习周期数的平均值，实验结果如图2所示。

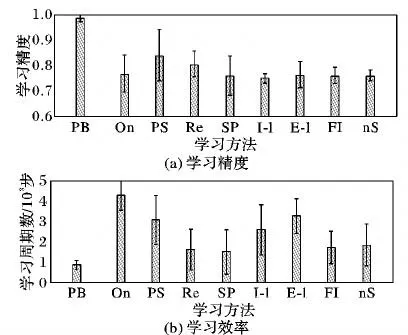
图2 当脉冲序列长度为1600 ms，期望输出激发率为100 Hz时的学习结果Fig.2 Learning results when the length of spike sequence is 1600 ms and the desired output excitation rate is 100 Hz

图2 中，PBSNLR具有最高的精度(C=0.95)和效率，这一点也符合文献［33］的结论。这再次验证了PBSNLR独特的离线学习机制可以获得很高的性能。在其他方法中，因为权值调整规则与LIF神经元模型密切相关，所以在5000步学习周期以内，PSD的精度较高(C=0.82)，然后依次为ReSuMe和OnMSGDB。剩下的几种方法精度都在C=0.75左右。考察达到最高精度所需要的学习周期数，OnMSGDB和E-learning最多，这说明虽然基于梯度下降的方法可以获得较高的精度，但是效率普遍较低。PSD虽然具有较高的精度，但是也需要较多的学习周期。ReSuMe和SPAN的效率较高。由此说明，几种学习方法都可以比较有效地实现脉冲序列学习，除了PBSNLR之外总体上精度差别不明显，但是效率差异较明显。

第二组实验考察当期望输出脉冲序列激发率提高时各方法的性能。一个有400个突触的LIF神经元学习激发一个长度是1200 ms的序列，输入与输出脉冲序列分别为激发率为10 Hz和180 Hz。神经元的初始权值取区间(0，3.6·10－3)上的均匀分布。实验中最大的学习周期数依然设定为5000步，学习速率设定与上一组实验相同。实验结果如图3所示。

由图3可知，在5 000步学习周期内，PBSNLR依然获得最高的精度，说明期望输出脉冲序列激发率的增加没有显著影响其优势。OnMSGDB的精度(C=0.88)和E-learning的精度(C=0.80)也高于其他几种学习方法。这说明基于梯度下降的学习方法在输出脉冲激发率较高时具有较强的学习能力。在其他几种方法中，PSD与FILT的精度依然较高，但是总体上相差不明显(值大约都在0.72～0.80内)。观察学习周期，此时各种方法差别更大。其中OnMSGDB需要的学习周期数最多，其次是Chronotron和PSD。和上一组实验类似，PBSNLR和SPAN的效率最高，仅需要大约500步学习就达到了最高精度。

综合图2和图3可知，两种情况下PBSNLR的学习性能最强。两种基于梯度下降的方法以及PSD具有较高的学习精度，但是这三种方法都需要较多的学习周期。虽然学习精度较低，但是SPAN却是效率最高的学习方法。ReSuMe的综合性能较好，并且对各种神经元模型的适应性最好，因此是较好的学习方法。

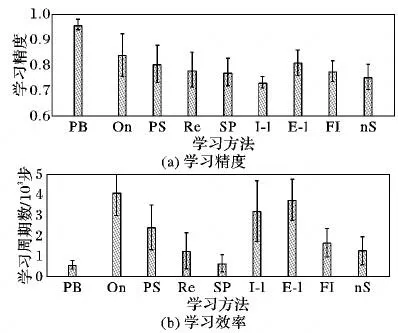
图3 当脉冲序列长度为1200 ms，期望输出激发率为180 Hz时的学习结果Fig.3 Learning results when the length of spike sequence is 1200 ms and the desired output excitation rate is 180 Hz

3.2 各种方法性能与特点的分析

不同学习方法在实验中性能的差异主要是由不同的学习机制造成的。PBSNLR采用独特的离线学习方式，在学习之前将数据全部转换成感知机的输入，训练开始后就完全脱离脉冲神经元的运行。这是其获得最高精度与效率的原因，同时也因此使得该方法与脉冲神经元内在联系偏弱。另外该方法自身也受到很多因素的影响，比如运行时间上反例点的选择、神经元运行时间离散的精度等，不同的设定可能对学习结果造成较大的影响。因此PBSNLR更适合作为一种衡量其他具有更好生物学基础学习方法的性能指标。

基于梯度下降的方法调整实际输出脉冲的激发时间不断地靠近对应的期望输出脉冲时刻。在调整激发时刻的同时还要控制权值调整的幅度以免当前脉冲激发被抑制或者又出现额外的脉冲激发，因此权值调整必须控制在一个合理的范围内。这是实验中选择较小学习速率的原因，同时也导致它的收敛速度较慢，在5000步内达到最高精度需要的学习周期数最多。但是这种权值调整方式也使其可以更加精细地控制实际输出脉冲的激发时间，这又使其学习精度具有更好的上升性。这体现在学习精度随着周期数的增加还可以显著增加，例如在第一组实验中，当学习周期上线增加至20 000，OnMSGDB的学习精度可以从C=0.75增加至C=0.90左右。

基于梯度下降学习方法的另一个优势体现在高激发率期望输出序列的学习中。实验结果显示其精度高于除PBSNLR以外的其他学习方法，这一优势的主要原因还是来自于其学习机制。两种基于梯度的下降方法都需要控制实际输出脉冲的激发时间靠近对应期望输出脉冲的时刻。期望输出脉冲序列的激发率提高，虽然会增加脉冲的数量，但是也会导致对应实际与期望输出脉冲之间的时间差别分布更加平均，从而降低调整实际输出脉冲激发时间的难度。

其他的几种学习方法都可以以在线方式运行，在线学习过程中几乎都可以采用类似ReSuMe的权值调整方式，即在期望输出脉冲时刻增强权值以激励其激发，在实际输出脉冲时刻减弱权值以抑制其激发。这种权值调整机制直接针对输出脉冲增强或者减弱权值，因此权值调整的效果明显，收敛速度较快。这体现在实验中几种方法达到最高精度的学习周期数都明显少于基于梯度下降的方法。但是这种机制在学习过程中达到精度上限后权值增强与减弱达到平衡，此时再增加学习周期或者改变学习速率其精度的提高都不明显。在这几个方法中PSD的精度最高，PSD仅仅对输入脉冲序列进行卷积处理，并且采用与神经元内部相同的卷积核函数，因此其尽量保留了脉冲神经元的特征，同时采用与神经元最直接相关的信息调整权值。

下面对脉冲序列学习方法进行简单的总结。首先，每一种学习方法都遵循一定的理论基础，这些理论基础往往衍生于传统神经网络已有的研究结果。例如，ReSuMe、SPAN、nSTK和PSD方法都是基于Widrow-Hoff规则，ReSuMe方法采用学习窗口函数来将Widrow-Hoff规则应用于离散的脉冲激发时间，而SPAN、nSTK和PSD方法都是采用卷积方式达到这个目的，FILT方法虽然始于随机模型，但是转换为确定性方法后依然采用类似于ReSuMe的窗口函数调整权值。从某种程度上来说窗口函数与卷积核函数本质上是类似的，不同的是函数的形式和处理的对象。PBSNLR直接采用了感知机规则进行学习。OnMSGDB和E-learning则是利用梯度下降法最小化实际输出与期望输出之间的差别，它们之间的区别则在于误差的计算与表示方法。

除了学习方法的理论基础，另一个区分各种不同方法的依据为学习时权值调整采用的计算方法。无论是哪种学习方法，针对一条突触权值的调整都要依据沿着这条突触到达神经元的输入脉冲信息，所不同的是以何种方式根据输入脉冲信息计算权值的调整幅度。在上述方法中，OnMSGDB和E-learning方法的权值更新计算公式中都以输入脉冲引起的突触后电位(PSP)作为权值调整的核心组成部分。PBSNLR在离散时间点计算感知机输入时也基于PSP，所以这一类基于SRM神经元模型的方法可以总结为突触后电位调整方法。PSD、SPAN、I-learning都是基于LIF神经元提出，并且都采用卷积方法计算权值调整。PSD采用与神经元膜电位表达式相同的卷积核函数对输入脉冲序列作用卷积，I-learning在此基础上在权值调整时携带了该突触的权值信息。SPAN则可以选择多种卷积核函数并且对输入、期望与输出脉冲序列都进行卷积计算。nSTK在卷积的基础上增加了非线性函数。FILT方法采用了独特的权值调整函数，使得输出脉冲之后传输进神经元的输入脉冲也成为有效的突触调整信息。ReSuMe方法利用学习窗口函数计算调整权值，由于可以选用不同的窗口函数，因此体现出较高的灵活性。对几种方法的综合分析与对比结果如表2所示。

3.3 目前存在的问题

目前脉冲神经元脉冲序列学习方法的研究还存在如下几个问题。

脉冲神经元是构建脉冲神经网络的基本单元，脉冲神经网络相对于单神经元来说无论是应用性能还是生物学的合理性都更强。多层脉冲神经网络的学习方法往往以单神经元的学习方法为基础。目前，除了OnMSGDB方法因其梯度下降的特性可以比较方便地扩展到多层网络的学习，其他方法都缺乏直接推广到多层网络的机制。已有的关于多层网络学习的研究结果中层与层之间往往缺乏内在联系，即前层和后层相互独立，分别负责不同的功能。例如在文献［39］中，前层完成对模式的编码，而后层利用单神经元的Tempotron方法实现对模式的分类。在神经网络研究中，网络层与层之间使用紧密联系的统一学习机制是更加合理的策略，因此，如何将多种脉冲序列学习方法推广到多层网络实现多层网络的序列学习是一个非常值得研究的问题。

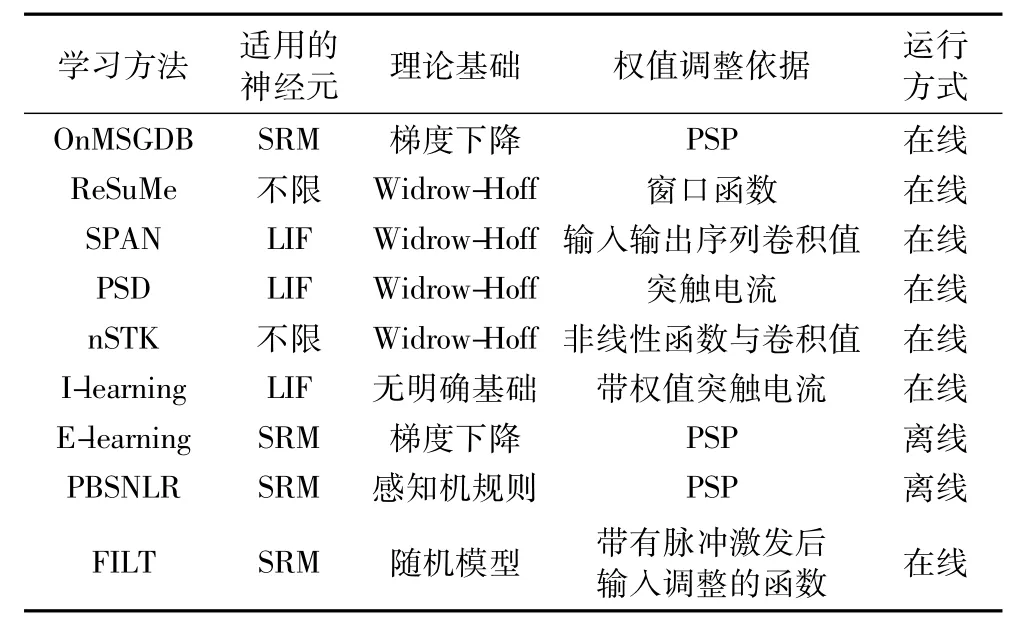
表2 多种脉冲序列学习方法的比较Tab.2 Comparison of different spike sequence learning methods

目前脉冲序列学习方法的研究中缺乏对于序列整体可学习性的评价方法。脉冲序列学习的性能除了和方法本身有关，还和输入、输出脉冲序列的特点有关。脉冲序列激发率、脉冲激发时间间隔、输入与期望输出脉冲的位置关系等都可以影响学习性能，而目前为止缺乏一个从序列本身出发的对于整个学习可能达到性能的评价方法。

目前大多数研究者都从偏向生物学模拟的角度将重点放在序列本身的学习能力上，而对于脉冲序列学习的应用研究略有不足。已有的脉冲神经元应用研究主要集中在如下几个方面:通过将模式用脉冲序列进行编码从而使用脉冲序列学习方法进行模式的识别和分类［40－41］;对于脉冲序列模式或者用脉冲序列进行编码的普通模式的存储［25］;对于某些易于用脉冲序列表达的特殊信号如疾病脑电波信号的识别［18］;利用脉冲序列编码图形从而实现图像的分类［42］等。

这些应用中一部分是基于传统神经网络的应用方式在脉冲神经网络上的扩展，一部分则是基于脉冲序列特点的与脉冲神经元适应性更高的应用方式。这些应用中通用的方式是将应用对象用脉冲序列进行编码，然后使用学习方法调整权值，从而得到期望输出脉冲序列。因此，脉冲序列编码方式、神经元参数选择、学习方法的选择为脉冲神经元应用的三个要素。

但是总体来看目前脉冲神经元的应用研究还比较简单，并没有很好地体现出脉冲神经元与脉冲序列学习方法的特点和优势。由于脉冲神经元模拟真实生物神经元的运行方式，因此其对于模拟人脑复杂模式的记忆、识别、分类，动作控制等，甚至更进一步模拟更加高级的智能活动都具有潜在的优势。另外，脉冲序列的时间特性还使得脉冲神经网络适合于解决与时间相关的问题，如连续动作图像的识别等。脉冲神经元应用研究关键在于如何将实际应用的对象用最合适的脉冲序列表示出来，并且如何确定最合适的神经元模型和参数。

4 结语

脉冲神经元的运行方式完全模拟真实的生物神经元，脉冲序列学习是脉冲神经元特有的有监督学习方式，对脉冲神经网络理论和应用的研究具有重要意义。本文较全面地介绍了典型的脉冲序列学习方法，详细阐述了它们的理论基础和特点并且通过实验比较了它们的学习性能。本文的研究结果可以作为脉冲序列学习应用与进一步研究的基础，进而可以有效地推动整个脉冲神经网络学习理论的发展和完善。