斯特林制冷机自适应主动振动抑制算法研究

李 娟，周 吉

（北京空间机电研究所 中国空间技术研究院空间光学遥感器技术核心专业实验室，北京 100094）

0 引言

随着空间遥感任务对精度要求的提高，卫星上的有效载荷对振动环境也提出了更高要求。机械制冷机产生的振动会对星载仪器产生极大的危害，是影响其空间应用的一个关键因素。目前国际上红外光电探测项目依赖于长寿命机械制冷机的成功应用。由于运动部件和气体穿梭导致制冷机产生振动干扰，尤其是冷指的振动会使红外探测器、焦平面器件偏离仪器光学系统的正常范围，导致成像模糊，对探测目标的分辨率和定位精度下降，甚至引起其他设备、结构的机械共振[1-3]。随着深空高分辨率观测、红外干涉等空间技术的发展，对振动的要求越来越苛刻，必须对输出的振动力进行抑制。

美、欧等国已开展机械制冷机的主动振动抑制算法研究，其中包括JPL（Jetpropulsion Laboratory）[4]、NASA（National Aeronauticsand Space Administration）[5]、Hughes（即 现 在 的 Raytheon）[6]、Lockheed、Sunpower等。占主流地位的是自适应前馈控制方法，其基本原理是利用机械致动器，根据其传递函数在每个谐波频率点产生一定的反振动力，使之与制冷机的原始振动力幅度相等、相位相反，从而达到振动抑制目的。该方法依赖于减振致动器传递函数，因此稳定性、收敛性受传递函数误差的制约，收敛时间较慢[7]。为克服同类振动抑制算法的缺点，从自适应滤波的角度，提出了新的控制算法，大幅提高了振动抑制的稳定性和收敛性。

1 自适应主动振动抑制系统模型

基于filtered-X LMS算法的自适应前馈控制方法算法简单易于实现，且对于线性主动控制系统具有较好的稳定性和可靠性，因而在主动振动抑制中应用最为广泛。众所周知，在自适应信号处理领域仿射投影算法和快速仿射投影算法是收敛速率和计算复杂度之间的折中。虽然这些算法通常不能提供像RLS算法一样的收敛速率，但是与随机梯度算法相比，收敛速率已有很大的提高，与递归最小二乘算法相比，计算复杂度低、稳定性也更高。在这里，仿射投影和快速仿射投影算法被引入到主动振动抑制中。图1是利用自适应FIR滤波进行主动振动抑制的框图。在filtered-X LMS算法中，如果信号有延迟，自适应滤波器的变化不会立即对误差信号产生影响，使得收敛增益μ只能选取很小的值，基于稳态系统的假设自适应滤波器系数变化很缓慢[8]。为了克服这个问题，引入了修正filtered-X滤波器结构[9]，自适应滤波器的任何变化都会及时的反应到新的误差信号，即使有信号延迟，相对于filtered-X LMS算法收敛增益μ仍然可以选取很大的值。

图1 延迟补偿修正filtered-X滤波器结构框图Fig.1 Delay compensated modified filtered-X structure

仿射投影算法的数学推导在这里不再赘述[10]，快速仿射投影算法最初的推导见文献[11-12]，用于主动噪声控制的自适应快速仿射投影算法在文献[13]中有详细地阐述，快速仿射投影算法通过计算“辅助系数”来替代“标准”时域自适应滤波器系数。这里主要研究的是基于延迟补偿修正filtered-X结构的仿射投影算法和其快速实现（MFXFAP）。在这里，所选择的快速仿射投影算法选用了内置滑动窗递归最小二乘算法来计算矩阵求逆，因此是利用延迟补偿修正filtered-X结构的FAP-RLS算法，亦可称之为MFXFAP-RLS算法。算法流程如式（1）～式（13）。

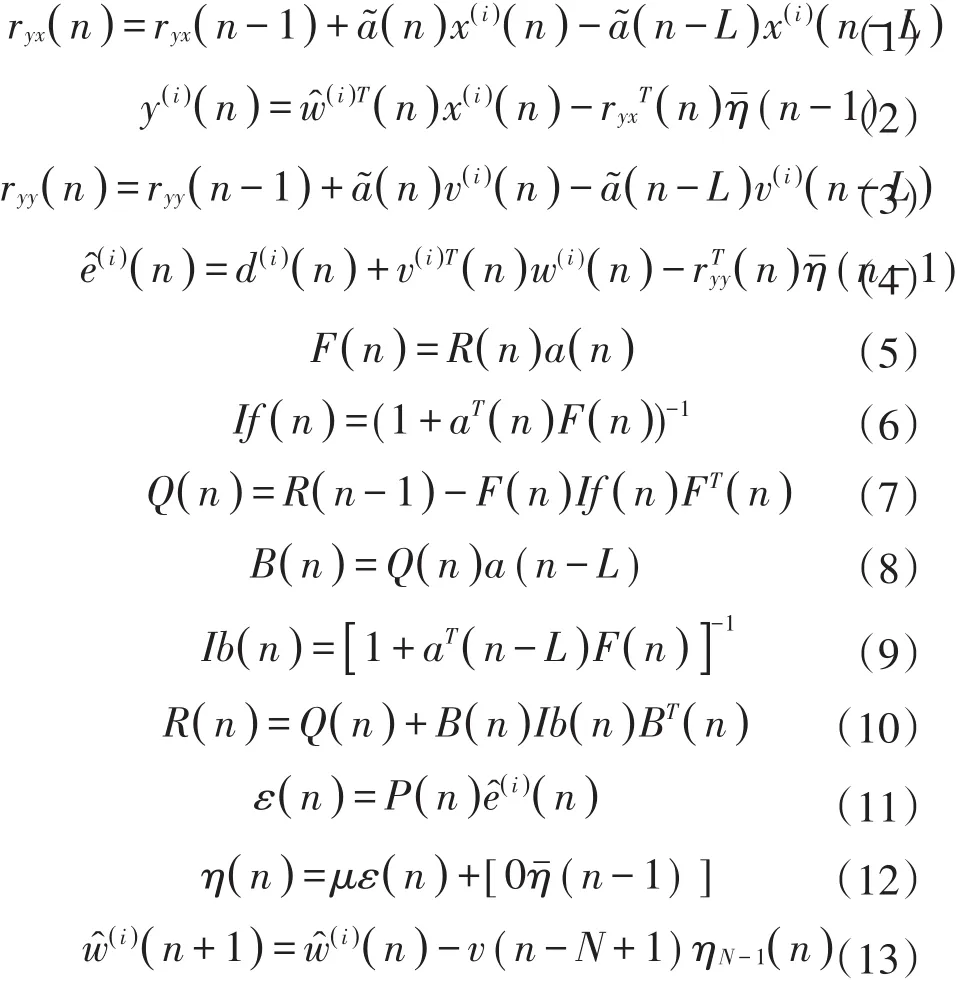
式中：L为自适应滤波器的长度；P为仿射投影阶数；M为估计模型中已知滤波器的阶数；为n时刻的参考信号为n时刻的滤波后信号为n时刻的目标信号为 延迟补偿修正filtered-X滤波器所计算的n时刻“替换”误差信号为 自适应FIR滤波器n时刻的第l个系数；为n时刻由估计模型滤波后的信号；为n时刻的自适应滤波器第l个“辅助”系数，这些辅助系数由快速仿射投影算法计算得出，与不同，仿射投影算法利用额外的方程从而不是中计算和)为滑动窗递归最小二乘算法中用到的逆相关矩阵，用单位阵乘以，对进行初始化，δ是正则化参数为矩阵的第一列为N-1个元素的相关向量，初始值设为为N-1个元素的相关向量，初始值设为0；为N个元素的误差向量的前N-1个元素的最后一个元素的最后N-1个元素。

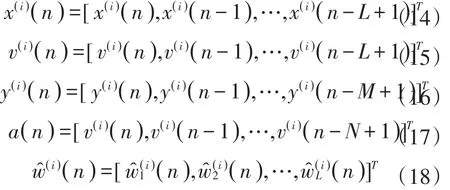
式中：μ为归一化的收敛增益；δ为正则化参数用以保持数值稳定，值得注意的是仿射投影算法的性能对正则化参数δ非常敏感，需慎重选择。

同有源消声技术类似主动振动抑制是利用一定的控制策略产生次振动与干扰振动相叠加，从而减少振动的传递。根据振动抑制的基本原理，自适应主动振动抑制系统模型如图2所示。该系统由控制器和传感器组成，控制器是核心，包括外部电路和控制软件。压缩机驱动信号分成了两部分，一路直接由参考信号驱动；另一路为叠加了振动抑制信号后的驱动，其中振动抑制输出产生了一个反振动力，与原来的振动实现线性叠加后抵消。因为压缩机的振动尤其是高阶振动会受环境条件变化的影响，需要实时监测，所以振动抑制效果由振动传感器反馈给控制器以便实时进行控制参数调整。

图2 自适应主动振动抑制系统图Fig.2 The diagram of adaptive active vibration control system

2 自适应主动振动抑制系统仿真分析

用Matlab进行了仿真实验，对应图2中的变量假设：x是频率为50 Hz的正弦波信号；v是经过估计模型滤波之后的信号，含有x的若干次离散谐波；d是x的延迟信号；e为自适应迭代的误差信号；采样频率为1 000/s，信号迭代次数选择为1 000；μ是归一化的收敛增益，取0.1；δ是正则化参数，取0.1。图3为参考信号x的时域表示，即幅值为1 Nrms的正弦波信号；图4为经过经估计模型滤波后演变为一系列频域上离散谐波，幅值由0 dB依次衰减；图5为参考信号经过时域延迟后的信号，幅值为1 Nrms的正弦波信号；图6为自适应滤波的误差信号，可以看出误差信号从±1 Nrms收敛至0 Nrms附近大概用了0.5 s。误差信号完全收敛说明两台电机产生的机械振动力基本完全抵消。

图3 参考信号x时域表示曲线

Fig.3 Reference signal x in the time domain

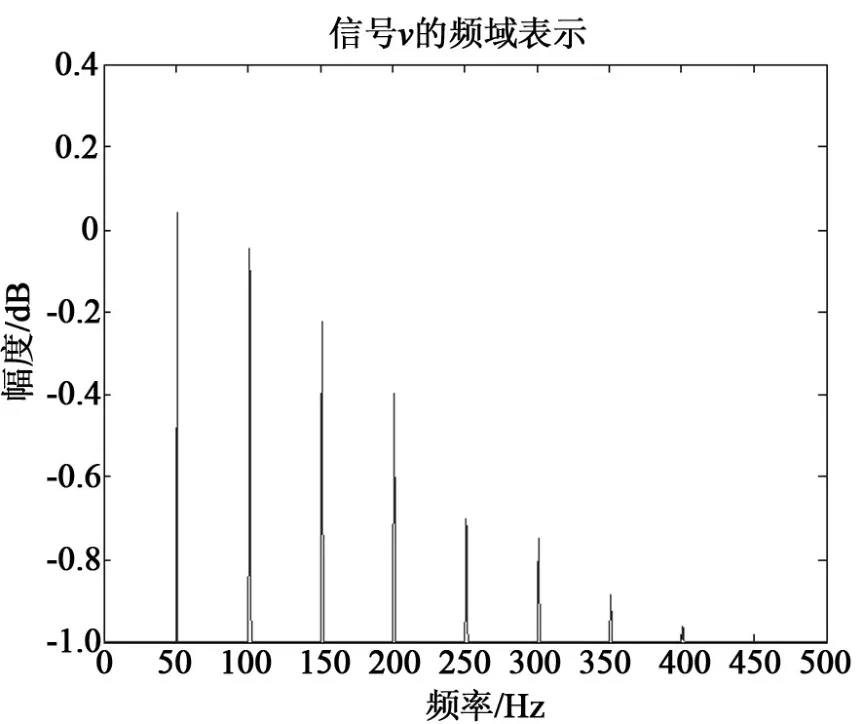
图4 经估计模型滤波后的信号v的频域表示曲线Fig.4 Filtered signal v by estimated model in the frequency domain

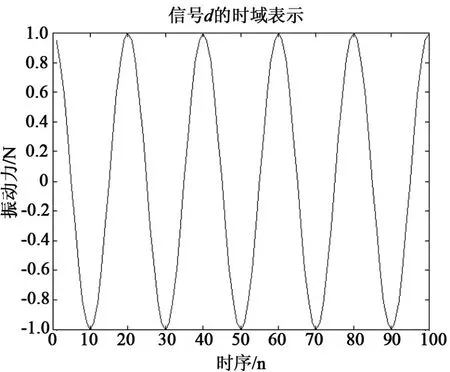
图5 延迟信号d的时域表示曲线Fig.5 Delayed signal d in the time domain

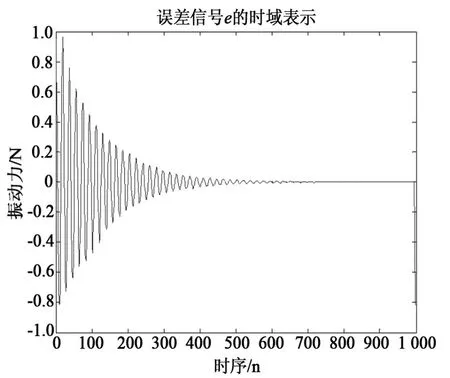
图6 自适应迭代误差信号e曲线Fig.6 Error signal of adaptive iteration

由图2可知基于与模型无关的随机梯度估计理论的自适应滤波算法用于制冷机减振时无需实际减振器的传递函数，因此摆脱了减震器传递函数误差的影响。由表1可知与随机梯度算法相比，收敛速率已有很大的提高，与递归最小二乘算法相比，计算复杂度低、稳定性也更高。由于引入了修正filtered-X滤波器结构，自适应滤波器的任何变化都会及时的反应到新的误差信号，即使有信号延迟，相对于filtered-X LMS算法收敛增益μ仍然可以选取很大的值，因而收敛性更好。

3 结论

要实现适合于空间应用的主动振动抑制需要深入理解机械制冷机振动特性与产生机理；了解如何提高对振动抑制器传递函数误差的容忍能力；研究主动振动抑制算法的收敛性、稳定性与适应性。在自适应信号处理领域，基于与模型无关的随机梯度估计理论的自适应滤波算法用于制冷机减振时无需实际减振器的传递函数，因此可以摆脱受传递函数误差影响的制约。自适应仿射投影算法和快速仿射投影算法是收敛速率和计算复杂度之间的折中。虽然这些算法通常不能提供像RLS算法一样的收敛速率，但是收敛速率已有很大的提高，与递归最小二乘算法相比，计算复杂度低、稳定性也更高。