微型拉瓦尔喷管的流体仿真分析和优化
2018-08-27喻巍岭冯煜东曹生珠张晓宇
喻巍岭,冯煜东,周 晖,曹生珠,张晓宇
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)
0 引言
液化气推进是冷气推进的一种,指工质液化后以气液共存的形式贮存于密闭容器内,当打开阀门后,在液化气自身饱和蒸气压的作用下,以气体的形式喷出[1]产生推力的方式。因液化气工质存储密度高、压力要求低,省去了高压气瓶等影响集成度和质量的部件与结构。因此具有无污染、控制冲量小、成本低、结构简单、可靠性高,适合微小卫星应用的优点。基于非硅基MEMS技术[2-3]的液化气微推进系统[4]具有微型模块化的特点,主要应用于立方星上。在上个世纪末至本世纪初,国外基于非硅基MEMS技术的液化气微推进系统已在轨成功验证并多次获得应用,同时采用非硅基MEMS加工的高集成度一体化平面管道、阀门、喷嘴设计可省去传统管道、接头带来的复杂结构和较大的体积和质量资源占用[5]。从而可大幅提高系统集成度、缩小质量和体积。实现在立方星所能承受的资源条件下为其提供基于推进系统的姿轨控能力,为高性能、低成本卫星技术和任务模式提供技术支撑。因此,基于微机电系统的液化气推进技术在微小型化方面具有独特的优势,在未来的航天任务中将会有非常大的发展潜力和优势。
1 数学模型
1.1 拉瓦尔喷管结构
微推进系统的喷管采用拉瓦尔喷管,示意图如图1所示。
从图1可以看出,拉瓦尔喷管共有五个尺寸因素:入口直径、喉部直径、出口直径、收缩段长度和扩张段长度,为毫米量级。喷管的主要性能指标为推力和有效比冲。研究中要求喷管推力F≥50 mN,有效比冲Isp≥50 s,与当前国外微推进系统性能水平基本一致。确定微推进系统的推进剂,通过对喷管的仿真分析和优化,得到优化结果。
1.2 控制方程
对于拉瓦尔喷管而言,喷管内的流动可视为定常、一维流动,而且在流动过程中满足绝热和无摩擦的条件[6-7]。同时,理想状态下的喷管流动还满足能量守恒方程、连续性方程(质量守恒方程)、动量守恒方程、理想气体定律和等熵过程方程。
(1)能量守恒方程:

(2)连续性方程:

(3)动量守恒方程:
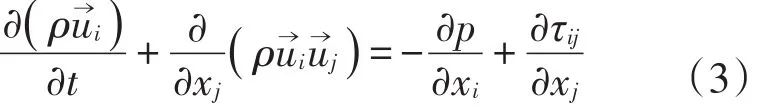
式中:ρ为密度;u为速度矢量;p为静压,τ为黏性应力张量;E为单位质量的总能量;q为热通量。
(4)理想气体定律。对于理想气体,其状态参数满足式(4)规律:

(5)等熵过程方程。气体在喷管中的流动可以看作一个等熵过程,其表达式为:

利用连续性方程、等熵关系方程及排气速度公式不难得到一般条件(流管中不一定会存在临界截面的情形)下通过某一截面x的理想气体定常等熵流动的质量流量公式:

由能量守恒方程可得:

式中:ic和ie分别为单位质量工质在喷管入口截面c和喷管出口截面e的焓;vc为工质在喷管入口截面c的速度。
又流动为等熵流动,根据等熵方程式,可以将式(7)改写为:

一般情形下喷管的推力公式为:

代入式(9)中,推力公式[7-10]可以改写为:

或可表示为:

其中:

式中:k为比热比;p0为入口压力;pe为出口压力;pb为环境压力,取0.001 Pa,近似为0;At为喉部截面面积;Ae为出口截面面积。
有效比冲指单位推进剂的量所产生的冲量,用质量来描述推进剂的量,则比冲拥有时间量纲,如式(13):

式中:Isp为有效比冲,s;g0为标准重力加速度,值为常数,不随所处引力场位置变化而变化,取9.8 m/s2。
2 推进剂选择
作为液化气推进剂的气体一般具有的性质为:可常温下液化贮存,其液态密度远高于气态密度;推进剂的液化压力较低,不需要配置高压气瓶和管路来贮存和输送,从而可降低推进系统的系统质量;比冲较大,在达到相同总冲时所需推进剂质量较小;无毒性,不易燃,从而可免除推进剂加注时的严格防护,降低发射和制造成本。
目前已实际应用的几种液化气推进剂有丙烷(C3H8)、异丁烷(C4H10)、氨(NH3)和一氧化二氮(N2O)等,性能如表1所列。
表1 所列几种液化气推进剂中,一氧化二氮贮存压力远高于其他三种推进剂的贮存压力,造成贮存单元和系统管路质量较大,系统质量难以满足微纳卫星的要求。如图2所示,常用的丙烷、异丁烷和氨三种推进剂中,虽然氨的饱和蒸气压与丙烷相当,贮箱压力也相对较低,且比冲较高,但是氨的气化热较大,充分气化需要的加热功率较大。如图3所示,丙烷和异丁烷在性能上差别不大。两者密度比冲接近,推进系统简单,质量较小,气化热比较接近,具有无毒、无污染和贮存压力低的特点,在微纳卫星上得到广泛应用。但在同等温度条件下,丙烷的饱和蒸气压大约是异丁烷的三倍,这有利于获得更大的推力比冲,因此选择丙烷作为推进剂。

表1 几种液化气推进剂的性能Table1 Properties of several liquefied gas propellants
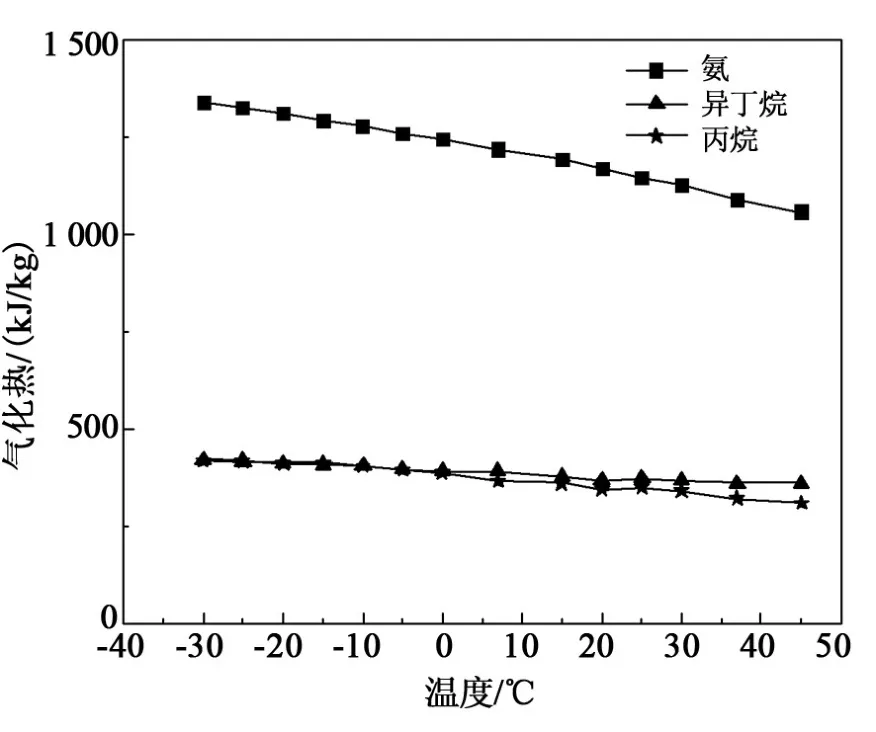
图2 氨、丙烷和异丁烷的气化热曲线Fig.2 Vaporization heat of ammonia,propane and isobutane

图3 丙烷与异丁烷的饱和蒸气压曲线Fig.3 Saturated vapor pressure of propane and isobutane
3 流体仿真
3.1 仿真参数设置
流体仿真对象为微喷管,参数取值为绝对值;求解器类型为基于密度且稳态轴对称的类型;模型为无黏模型并满足能量方程,流体为理想气体状态的丙烷;边界条件包括压力入口边界条件、压力出口边界条件、轴对称边界条件和壁面边界条件。由于推进剂以饱和蒸气压的压力从贮箱进入管道,因管道较短忽略其压力损失,所以压力入口边界条件取推进剂饱和蒸气压,约为0.9 MPa;出口压力取0.001 Pa,近似为0。此外,初始温度取300 K,其余参数默认。求解方法为二阶迎风耦合隐性,适用于高速可压流体,所有参数残差皆取10-5。
3.2 仿真结果
流体仿真采用正交试验[11-12]优化方法,可以得到一定范围内的推力和有效比冲。正交试验优化方法是一种可以研究多因素、多水平的设计方法,正交性从全面试验中挑选出部分有代表性的点进行试验,这些点具备了“均匀分散,齐整可比”的特点,是一种高效率、快速、经济的实验设计方法。
根据正交试验结果得知,在入口直径1~3 mm、喉部直径0.3~0.9 mm、出口直径1.2~3.6 mm、收缩段长度0.4~2.0 mm、扩张段长度2~8 mm范围内时,推力范围大致在100~1 000 mN之间,有效比冲范围大致在50~80 s之间。出口直径的极差为15.26,对目标函数的影响最大;喉部直径的极差为13.42,对目标函数的影响次之;收缩段长度的极差为3.73,对目标函数的影响次之;入口直径的极差为1.18,对目标函数的影响次之;扩张段长度的极差为0.29,对目标函数的影响最小。后三个因素的极差相比前两者小很多,视为次要因素。
由比冲和推力要求较低,可以适当减小喷管尺寸,以减小喷管结构大小和质量。因此,从正交实验中选择有效比冲为72.66 s,推力为120.58 mN的试验结果作为初始值,进行单项因素优化。

图4 喉部直径对推力和有效比冲的影响曲线Fig.4 Effect of throat diameter on thrust and effective specific impulse
从图4中可以看出,喉部直径对有效比冲和推力的影响很明显。喉部直径越大,有效比冲越小,推力越大。在同等初始温度和压力的条件下,由于入口压力不变,喉部直径的增加,会使得处于扩张段的气流压力降得更快,流体速度与之相比也会有所减小。在单位时间内从喷口喷出的流体质量增加,推力增加是必然的。由推力公式亦可得知,推力与喉部直径是正相关的。对于有效比冲,虽然喉部直径的增加导致了推力的增大,但同时质量流量也有很大增加,因此有效比冲变化幅度较小,随喉部直径增加而有所减小。
当喉部直径为0.1 mm时推力14.83 mN,不满足推力要求;喉部直径为0.2 mm时推力56.01 mN,基本达到推力要求。又由有效比冲要求,喉部直径越小越好。因此,喉部直径选择在0.2~0.3 mm之间。
从图5中可以看出,出口直径越大,有效比冲整体趋势增大,推力越大。在其他尺寸因素不变的条件下,出口直径越大,使得出口流体速度越大,质量流量越大,因而推力和有效比冲也会增大。从图中可以看出,在出口直径为1.8~2.0 mm的时候,有效比冲有一个明显的突降,推力增加幅度也有所减小。由于出口直径小于2.0 mm时,小于入口直径,质量流量较小;当出口直径等于入口直径时,质量流量有较大增加,而推力基本不变,因而造成有效比冲的突降。

图5 出口直径对推力和有效比冲的影响曲线Fig.5 Effect of outlet diameter on thrust and effective specific impulse
如图6所示,有效比冲在收缩段长度小于1 mm时变化较大,而在收缩段长度大于1 mm时几乎无变化。由于拉瓦尔喷管的特性,超声速气流必定在喉部直径出达到当地声速,因此在收缩段长度增加到一定值时,收缩段长度对有效比冲的影响会逐渐减小,即只有在收缩段长度较小时与有效比冲存在较好的耦合性。因此收缩段长度对质量流量和推力的影响也小,可认为推力变化与收缩段长度无关。因此,收缩段长度可以适当选择较小的数值,以减小结构尺寸,有利于推进器的集成。
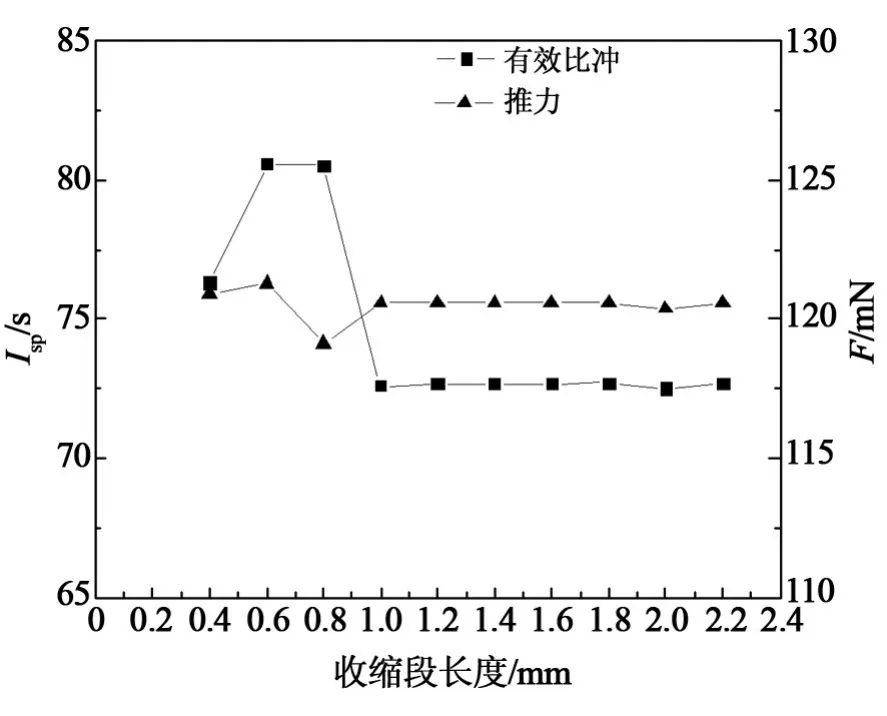
图6 收缩段长度对推力和有效比冲的影响曲线Fig.6 Effect of contraction length on thrust and effective specific impulse
如图7和图8所示,出口直径和扩张段长度的变化对质量流量等因素影响很小,入口直径和扩张段长度的改变对推力和有效比冲几乎没有影响,推力的差值小于0.4 mN,有效比冲的差值小于0.2 s,基本可以忽略不计。

图7 入口直径对推力和有效比冲的影响曲线Fig.7 Effect of inlet diameter on thrust and effective specific impulse

图8 扩张段长度对推力和有效比冲的影响曲线Fig.8 Effect of expansion length on thrust and effective specific impulse
因此,最后选择喉部直径、出口直径和收缩段长度三个因素在更小的范围进行优化,得出喷管的优化尺寸。使入口直径、扩张段长度分别固定为1 mm、2 mm,其余三个因素在一定尺寸范围内:喉部直径0.2~0.3 mm、出口直径0.8~1.2 mm和收缩段长度0.3~0.9 mm,进行正交试验得到一个较好的优化尺寸。最终,进一步仿真分析得到喷管优化尺寸为:入口直径1 mm,喉部直径0.25 mm,出口直径0.8 mm,收缩段长度0.6 mm,扩张段长度2 mm。此时,喷管有效比冲为69.80 s,推力为72.89 mN,质量流量为0.107 g/s,出口轴向平均速度可达620.67 m/s。
4 结论
采用Fluent软件对微型模块化液化气微推进系统的拉瓦尔喷管进行了仿真分析,得到了喷管各个尺寸因素对有效比冲和推力的影响关系,并给出了喷管的最终优化尺寸。
(1)出口直径、喉部直径和收缩段长度对有效比冲和推力的影响较大;入口直径和扩张段长度对有效比冲和推力的影响很小,可忽略不计。
(2)喉部直径越大,有效比冲越小,推力越大;出口直径越大,有效比冲和推力越大,收缩段长度在小于1 mm时对有效比冲有较大影响,对推力基本无影响。
(3)喷管最终优化尺寸为:入口直径1 mm,喉部直径0.25 mm,出口直径0.8 mm,收缩段长度0.6 mm,扩张段长度2 mm。喷管有效比冲为69.80 s,推力为72.89 mN,质量流量为0.107 g/s,出口轴向平均速度可达620.67 m/s。
