氮气在泡沫铜内的流动传热特性模拟研究

陈 曦，凌 飞

（上海理工大学能源与动力工程学院，上海 200093）

0 引言

多孔介质是由固体骨架和由骨架分隔成大量密集成群的微小孔隙所构成的一种复合介质。由于其结构的特殊性，多孔介质在材料、环境科学、能源与动力等学科领域有着广泛的研究和应用。金属泡沫是一种由金属固体骨架和泡沫气孔构成的不均匀的兼具功能和结构双重属性的典型多孔介质，具有优良的力学、热物理、电学和声学等特性[1]，在结构轻量化、能量吸收以及强化换热等方面均具有巨大的应用潜力[2]。金属泡沫优良的换热性能使其具有承受高密度热流的能力，在电子元器件热管理、紧凑型换热器等领域中有着广泛的应用[3]。对多孔介质理论的研究需要多学科相融合，是一项具有很高科研应用价值的基础性研究[4-5]。

多孔介质内部流动和传热过程十分复杂，理论分析难描述，试验测试相对可靠准确，但是由于金属泡沫的制作成本高，时间周期长，花费较大，因此试验研究也具有一定的局限性。近年来相关科学技术与理论的发展，如核磁共振、CT扫描成像以及格子-Boltzmann方法（LBM），格子气模型的建立等，使渗流力学的发展进入一个全新的阶段，尤其是高性能计算机的出现，为金属泡沫流动换热的数值模拟研究带来很大的方便。

目前金属泡沫模拟研究主要有两类方法：宏观尺度和孔尺度。宏观尺度模型忽略了具体孔隙结构分布和复杂固体边界面的影响，通过求解平均的N-S方程，得到多孔介质的流动情况，例如Ansys-Fluent软件的Porous模块基于这种方法。但因结构的概化，难以清晰考虑结构与宏观特性的关联。陶文铨[6]在均化孔隙结构的假设上，采用有限差分法，对泡沫金属的流动换热性能进行了模拟；王晓鲁等[7]对周期性的网状泡沫金属结构，采用软件进行类似的分析。孔尺度模拟建立在泡沫金属微观结构的基础上，Beugre等[8]应用相应泡沫金属样品的结构信息对渗透率进行了测算，并与实验进行了比较；Jeong等[9]在结构信息的基础上对质扩散率与热扩散率进行了模拟分析。采用孔尺度建模进行数值模拟能够真实地反映出孔隙内部流体的实际流动状态，但是在实际应用中也有一定的局限性，比如对孔隙空间随机无序分布的孔结构建模有一定的难度。因此，在模拟中常利用孔尺度理论模型进行周期性建模。另外，卢新伟[10]在宏观尺度和孔尺度下模拟金属泡沫流动换热，并且实现两种方法的对接，提供了一种新的模拟思路。

本文拟开展多孔介质流动传热的数值模拟。通过三维建模在低温制冷机冷头换热器中填充多孔介质泡沫铜，用ICEM划分三维结构网格，导入Fluent软件对氮气在泡沫铜内的流动换热情况进行模拟仿真，研究不同孔隙率、孔密度以及入口流速对流动、传热的影响。

1 控制方程

1.1 动量方程

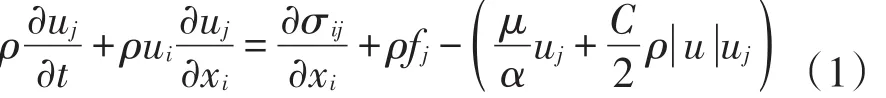
对比微观结构模型，宏观结构模型中去掉了固体骨架部分，固体骨架的几何形状对流场的影响因素用内部阻力和黏性阻力参数来表述。宏观尺度多孔介质流动数值模拟的控制方程主要是通过修改连续体介质的控制方程得到，如在流动标准动量守恒方程上增加动量源项，由黏性损失项和惯性损失项组成，如式（1）。式中：α为多孔介质的渗透性；C为惯性阻力因子，根据经验公式计算推导黏性和惯性阻力系数，其中Fourie[11]推导出牛顿流体在高孔隙率、各项同性的金属泡沫内流动的压降关系式，同时适应于Darcy以及Forchheimer模型。该模型以三维立方体为单胞的一种周期性结构来近似模拟通孔金属泡沫的拓扑结构，但仅能在高孔隙率范围内合理预测通孔金属泡沫的渗透率，为了扩展上述模型的适用范围，提出一个能够准确描述通孔金属泡沫三维流动迂曲度的模型，对合理预测金属泡沫的渗透率显得尤为重要和必要。Ahmadi[12]通过修改表征单元体积法（REV），消除了一些歧义，推导出适用于三维模型的式（2）：

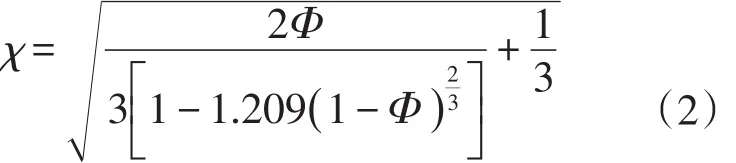
式中：χ为迂曲度；Φ为孔隙率。在Fourie经验公式的基础上，采用Ahmadi推导的公式修正迂曲度，计算黏性阻力系数和惯性阻力系数，在保证准确度的基础上扩展了经验公式的适用范围。

1.2 能量方程

宏观尺度多孔介质换热数值模拟，主要存在两种热分析模型，热力学平衡模型和非热力学平衡模型。非热力学平衡模型理论上可以提高计算精度，但在该模型需要根据经验公式计算骨架与流体之间的对流换热系数，以及多孔介质的比表面积，误差变相增大，综合考虑为了简化模拟，采用热力学平衡模型。在热力学平衡模型中引入了基于孔隙率的等效传热系数，如式（3）～（4）：

式中：Ef为流体总能量；Es为固体区域总能量；ρf为流体密度值；ρs为固体密度；Φ为孔隙率；ν→为流速；p为压力；∇keff、∇T为导热项；keff为多孔介质的等效传热系数，是流体导热率和固体导热率的体积平均值；∇∙为组分扩散项；)为黏性耗散项，τˉ为黏性应力；Shf为流体焓源项；kf为流体热传导率；ks为固体热传导率。

1.3 湍流方程

当多孔介质的几何尺寸对湍流涡结构产生影响时，不能单纯通过求解标准守恒方程计算湍流变量，需添加源项，在k～ε模型中Pedras[13]提出：

式中：Sk、Sε分别为湍流动能源项和湍流耗散率源项；C2为模型特定常数为流体平均流速；Ck=0.28，K为渗透率。

根据Pedras推导的湍流源项公式计算湍流动能和湍流耗散率源项。

2 仿真模型及边界条件

利用三维软件对模拟所需的内嵌多孔介质泡沫铜的低温制冷机冷头换热器进行建模，并通过ICEM划分三维结构网格，完成前处理。如图1所示，A为所研究的泡沫铜实体，泡沫铜前端左侧为圆柱形流体入口，右侧为流体出口，B为低温制冷机冷头换热器结构。

选择相应的控制方程，设置计算域边界条件，边界条件如表1所列；建立作为泡沫铜区域的网格单元，指定该区域为流体域，在此区域上开启多孔介质模型；进行多孔介质宏观参数设定，指定黏性阻力系数、内部阻力以及孔隙率等；选择热力学平衡模型进行热计算，指明骨架材料。另外，这里通过UDF指定泡沫铜黏性阻力系数、惯性阻力系数、湍流动能源项、湍流耗散率源项等。最后求解并对其速度场、压力场、温度场进行分析。

图1 冷头换热器结构网格图Fig.1 Cold head heat exchanger structure grid

表1 仿真模型边界条件Table1 Boundary condition of simulation model

3 模拟结果与分析

通过数值模拟可以得到泡沫铜结构内流体的速度场、压力损失以及氮气降温情况，分析各因素对氮气在泡沫铜内流动换热的影响。

3.1 速度场数值模拟结果

当泡沫铜孔隙率较大、孔密度较小时，流动的阻隔作用较小，速度衰减较慢，渗流性能较好，有可能形成环状流动；而泡沫铜孔隙率较小、孔密度较大时，速度衰减较快，仅入口处流速较快，其他区域流速较慢，如图2所示。

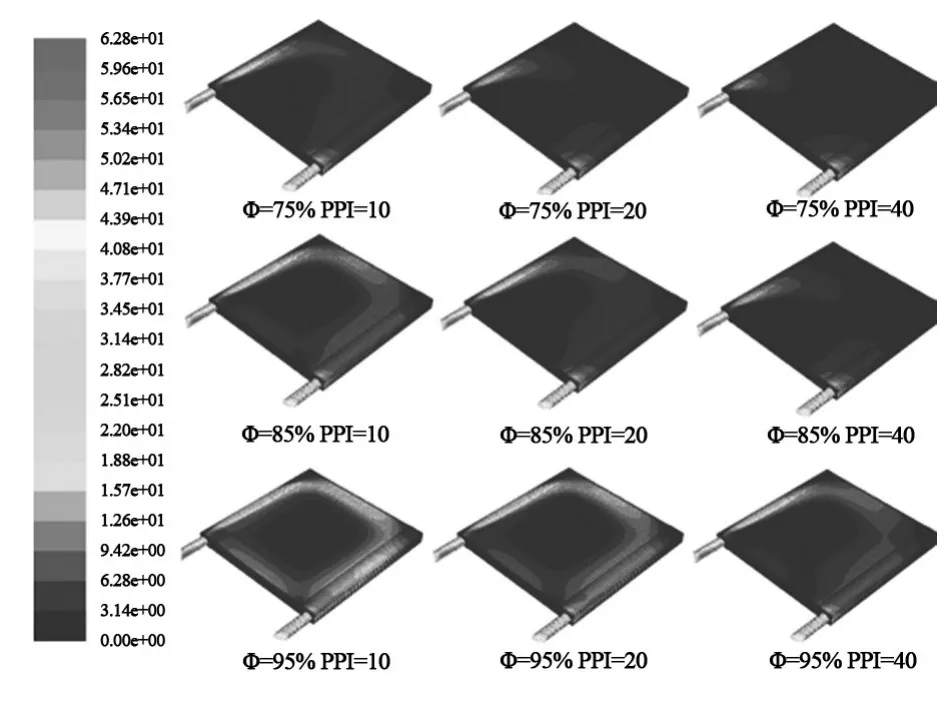
图2 入口流速v=30.0 m/s时的氮气速度云图Fig.2 Nitrogen velocity nephogram（v=30.0 m/s）

3.2 孔隙率对压力场和温度场的影响

当孔密度一定时，压力损失随流速的增加呈现线性增长趋势，低孔隙率泡沫铜的压力损失较大且随着流速的增大而增长得更快，主要是因为低孔隙率对于流动的阻隔作用在高流速下更为明显，随着孔隙率的增大，孔隙内部的通道更为通畅，阻隔作用小，有利于流动，如图3所示。

图3 不同孔隙率下的压力损失曲线Fig.3 Pressure losses under different porosity

随着孔隙率的增大，换热效果变差，因为比表面积随之减少，并且过高的孔隙也减弱了扰流的发生。随着孔隙率减小，换热效果不断提高，但提高的趋势渐缓，因此可能存在某一孔隙率，使得压损与温降的比值最小，即可能存在最优孔隙率，如图4所示。

图4 不同孔隙率下的氮气平均温度曲线Fig.4 Mean temperature of Nitrogen under different porosity

3.3 孔密度对压力场和温度场的影响

当孔隙率一定时，压力损失随流速的增加几乎呈现线性增长趋势，高孔密度泡沫铜的压力损失较大且随着流速的增大而增长得更快，主要是因为密集的孔洞对于流动的阻隔作用在高流速下更为明显，随着孔密度的增大，比表面积增大，从而由无滑移壁面引起的压力损失增大，如图5所示。

图5 不同孔密度下的压力损失曲线Fig.5 Pressure losses under different pore density

如图6所示，高孔密度时降温效果较差，流体平均温度较高，换热效果随孔密度的增高而降低。流体平均温度也随流速的增加呈现线性增长趋势，并非换热效果随流速的增大而降低，而是因为流速的增大，有更多的流体流入泡沫铜内，热负荷增大，从而整体降温效果不好。

图6 不同孔密度下的氮气平均温度曲线Fig.6 Mean temperature of Nitrogen under different pore density

4 结论

通过Fluent软件对泡沫铜内氮气的流动换热情况进行模拟仿真，研究不同孔隙率、孔密度及入口流速下的速度场、压力损失以及换热情况，得出结论：

（1）当泡沫铜孔隙率较大、孔密度较小时，渗流性能较好，氮气速度衰减较慢，有可能形成环状流动，反之速度衰减较快，仅入口处流速较快，其他区域流速较慢。

（2）孔密度一定时，泡沫铜内氮气压力损失随流速的增加几乎呈现线性增长趋势，低孔隙率泡沫铜的压力损失较大且随着流速的增大而增长得更快，低孔隙率对流动的阻隔作用在高流速下更为明显。随着孔隙率的减小，换热效果不断提高，但提高的趋势渐缓，因此可能存在某一孔隙率，使得压损与温降的比值最小，即可能存在最优孔隙率。

（3）孔隙率一定时，随着孔密度的增大，比表面积增大，由无滑移壁面引起的压力损失增大。高孔密度时降温效果较差，流体平均温度较高，换热效果随孔密度的增高而降低。