LTE-A系统中基于小区参考信号的信道估计算法

李慧敏，张治中，李琳潇

(1.重庆邮电大学 通信网与测试技术重点实验室，重庆 400065； 2.重庆重邮汇测通信技术有限公司，重庆 401121)(*通信作者电子邮箱lihuiminMM1009@163.com)

0 引言

增强型长期演进(Long Term Evolution-Advanced, LTE-A)系统的物理层核心技术为正交频分复用(Orthogonal Frequency Division Multiplexing， OFDM)技术和多输入多输出(Multiple-Input Multiple-Output, MIMO)技术。OFDM技术提高了频谱的利用率，并且能有效抗多径衰落，MIMO技术在不增加频率资源的前提下提高传输速率，而这些技术的性能需要良好的信道估计作为支撑，因此，信道估计是整个通信系统不可或缺的一部分，只有对信道进行准确估计，充分了解信道状态信息，才能在整体上提高无线通信系统的性能[1]。

LTE-A系统中通常采用基于参考信号的信道估计方法，对导频的信道估计值进行内插，从而得出数据子载波的信道冲击响应。这种方式有利于追踪信道变化，提升系统的整体性能。工程中经典的频域插值算法有基于离散傅里叶变换(Discrete Fourier Transform, DFT)的插值算法、线性插值、线性最小均方误差(Linear Minimum Mean Squared Error, LMMSE)插值。其中LMMSE频域插值算法性能较好，但要求信道先验信息且复杂度高，到目前为止，已经有很多文献对LMMSE算法进行改进，但往往对性能和算法复杂度进行单一考虑，性能较好的算法复杂度过高，复杂度低的算法精度却不太理想，达不到较好的折中，无法应用于实际的LTE-A系统。文献[2]通过对矩阵进行奇异值分解(Singular Value Decomposition, SVD)，使得算法复杂度有效降低，但它涉及到信道自相关矩阵和信道统计信息。文献[3]采用双对角矩阵的LMMSE信道估计方法，但是仍需知道信道统计信息，而实际中无法提前获取信道的统计信息。文献[4]借助托普利兹矩阵对自相关矩阵进行求取，无需提前获取信道二阶统计信息；但该算法复杂度过高，限制了实际应用。文献[5]通过离散小波变换对含噪信号量化处理，再结合经验模型分解和奇异值分解原理，降低了噪声的影响；但该算法的性能与小波分解层数的选取有关，当系数选取不可靠时，性能下降，易产生模型混叠问题。文献[6]利用门限定阶对信道自相关矩阵近似求取，无需预先知道信道先验统计信息；但该算法需要选出大量点来确定插值权重，算法运算量过大，仅适用于网络稳定的条件下。

针对上述算法需要预先获取自相关矩阵和信噪比(Signal-to-Noise Ratio, SNR)等信道先验知识以及算法复杂度大的问题，本文在现有的简化LMMSE算法的相关研究基础上，提出一种基于小区参考信号(Cell Reference Signal, CRS)的改进LMMSE算法。在借助导频值对自相关矩阵和信噪比进行合理估计后，再利用滑动窗来减小运算复杂度，从而确定LMMSE滤波插值矩阵，完成信道估计运算，达到算法性能与运算复杂度的折中，并与目前广泛使用的经典插值算法进行性能分析仿真对比。仿真实验结果表明：所提算法性能明显优于线性插值以及基于离散傅里叶变换的插值方法，且与传统LMMSE插值算法具有相近精确度。

1 改进算法设计思想

在LTE-A下行信道估计时，常采用基于参考信号的信道估计算法，一般是先估计出导频位置处的信道响应，然后内插得到数据位置的信道响应。基于CRS的整个信道估计流程可分为以下3个模块：

1)用最小二乘(Least Squares， LS)算法得到CRS位置初始信道估计值；

2)在频域进行LMMSE插值；

3)在时域进行线性插值，进而获得信道全响应。

1.1 CRS信道估计

LTE-A协议标准中定义了多种不同的参考信号，其中CRS可用于信道估计。图1描述了当采用天线端口0和1时CRS在时频资源网格中的位置[7]。

任何一个天线端口的资源元素(k,l)被用来发送参考信号，那么其他天线端口相同时隙的这个资源元素置零。对于两发送天线端口，一个无线帧内一共有4个OFDM符号含参考信号。每个发送天线端口在一个含参考信号的符号上频域1个资源块(Resource Block, RB)范围内有2个参考信号资源粒子(Resource Element, RE)[1]。

由于LS算法可满足下行的低功耗要求，易于实现，在实际工程中常用LS算法用于导频位置的信道估计，LS信道估计计算过程如下所述。

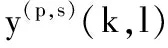
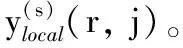
步骤3 对每个接收天线p和发送天线端口s进行LS信道估计：

(1)

其中(·)*表示共轭。

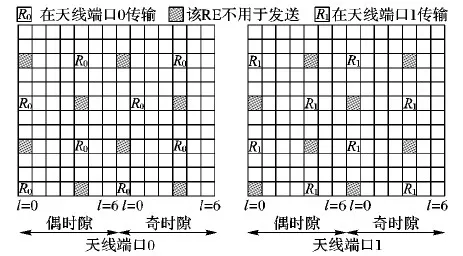
图1 CRS映射图样

为了提高信道估计的性能，本文在LS估计子模块后，以及频域LMMSE插值算法前，通过导频插值模块来增加虚拟导频。以天线端口0[8]为例，导频插值在一个子帧内进行，插值过程如图2所示。信道时域的变化速率取决于多普勒扩展大小，且成正相关，若多普勒扩展的值越大，信道时域上变化速率则越大。即使在多普勒频移高达300 Hz的情况下，信道的相关性仍然很强，因此可由已得到的导频信道相应值先行进行插值，相当于增添了虚拟导频，从而将导频加倍。

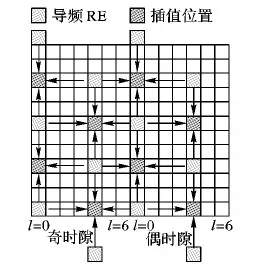
图2 导频插值结构

1.2 频域LMMSE内插

在LS算法基础上，进一步得到LMMSE信道估计插值算法[9-10]表达式为：

(2)

其中：W为频域滤波插值矩阵；RHHp为所有导频位置的信道自相关矩阵；RHpHp为数据位置和导频位置子载波的信道互相关矩阵；I为单位阵；β是取决于所采用调制方式的常数：若调制方式为正交相移键控(Quadrature Phase Shift Keying, QPSK)，β=1；对于16正交振幅调制(Quadrature Amplitude Modulation, QAM)，β=17/9；对于64QAM，β=2.685 4。

从上面可看出LMMSE插值算法的难点在于：信噪比和自相关矩阵两个未知量的求取以及大量矩阵求逆运算[11]。前者决定了算法性能，后者决定了运算复杂度。工程应用中，为了避免实时矩阵求逆导致运算量巨大，需要寻求复杂度和性能的折中。下面给出一系列解决方案。

1.2.1 信道相关矩阵

信道相关矩阵的值和所选信道模型紧密相关。常用信道模型呈多径均匀分布,功率延迟剖面为负指数分布，即θ(τ)=Ce-τ/τrms，则相关矩阵[12-13]为：

RHH=E{HHH}=[rm,n]

(3)

(4)

其中：τrms是均方根时延；L是最大多径时延。

由式(4)可以看出，信道自相关矩阵的值与τrms相关，但在实际工程应用中，时延参数往往是不可知的。众所周知，无线信道的传播环境十分复杂多变，如有诸多建筑的城市与平坦开阔的农村相比，时延参数也大有不同。传统做法通常把τrms取一个固定常数，由此可能导致所选参数值与当前信道不匹配，影响算法估计性能。

由以上分析可知，如若能在不同信道环境下对时延参数进行实时估计，并因此调整自相关矩阵的取值，可获得更好的信道估计性能。为解决传统算法造成的信道失配问题，提出一种对改进算法。由于时域内的信道能量比较集中，因而本算法是在时域内实现的，具体算法步骤如下所述。

1)合并导频LS信道估计值。

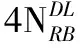
(5)

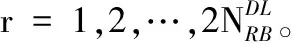
2)进行快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)。

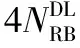
(6)

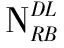
3)寻找信号最强径。

按照以下方式找到经过p根接收天线IFFT合并后的信号最强径对应的位置Dmax及其对应的能量Pmax：

(7)

Dmax=arg{max(Ps(i))}

(8)

其中：i=0,1,2,…,NIFFT-1；arg(·)表示求位置函数。

表1 资源块数和IFFT点数对应关系

4)寻找信号第一径。

从长度为M的搜索窗SW起始点开始，在搜索窗内查找功率大于信号最强径功率γ倍的第一个值，记录此第一个值的位置为信号的第一径位置Dfirst；如果没找到，则认为最强径就是信号的第一径。其中长度为M的搜索窗索引如下：

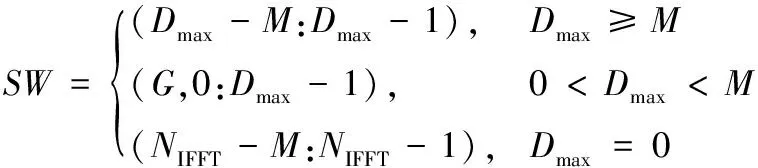
(9)

其中，G=(Dmax-M+NIFFT:NIFFT-1)，γ=1/3以及M=64。

5)计算门限。

步骤1 对Ps(i)进行重新排列得到Ps′(i)：

若Dfirst=0，

Ps′(i)=Ps(i);i=0,1,…,NIFFT-1

(10)

否则，按下面描述进行重新排列：

Ps′(i)=

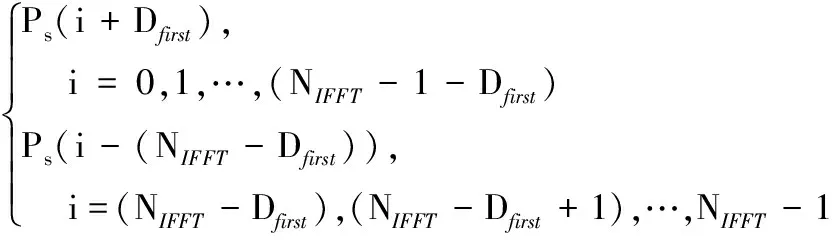
(11)

步骤2 根据步骤3)中的Pmax获得有用信号功率门限TP：

TP=Pmax/64

(12)

步骤3 求出噪声功率PN，并根据PN获得噪声门限TN：

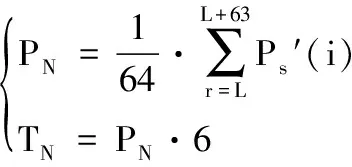
(13)

其中L为设置的多径条数。

6)挑选信号有效径。

在Ps′(i),i=0,1,…,L-1中找出大于等于max{TN,TP}的值，假设有N个值，记作Ps″(n),0≤n≤(N-1)，并记录其位置信息Pos(n),0≤n≤(N-1)。如果没有符合条件的值，则保留Ps′(i)中的最大值及其对应的位置信息。

7)计算均方根时延。

根据Ps″(n)和Pos计算等效的时延扩展均方根τrms：

τrms=

(14)

8)求信道相关矩阵。

把时延参数τrms代回式(4)即求得信道相关矩阵中的值。

τrms估计的总体框图如图3所示。

图3 均方根时延扩展估计过程

1.2.2 接收端SNR

SNR估计模块与自相关矩阵计算类似，需变换到时域进行。在基于上述过程计算出时域信道冲击响应能量Ps的基础上，求出能量Ps的均值Pave。按式(15)计算噪声能量：

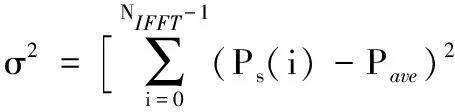
(15)

则接收端信噪比为：

SNR=Pave/σ2

(16)

1.2.3 矩阵求逆运算

LMMSE算法由于存在大量矩阵求逆导致算法复杂度过高，在保证性能的前提下，可通过W值预存和滑动窗来简化算法。

由式(2)可知，如果时延参数和SNR的估计结果发生变化时，滤波矩阵W也需要重新计算更新，即需要进行矩阵的大量求逆运算。在实际应用时，这种巨大的计算量是无法实现的，因此可将SNR和τrms分成几个区间，对LMMSE频域插值系数预先计算并存储，需要时根据估计结果选择调用相应的滤波插值系数。

当系统采用20 MHz带宽时，增加虚拟导频后，则一个OFDM符号内，子载波的个数和导频子载波个数分别为1 200和400，因而自相关矩阵RHpHp维数高达400×400，互相关矩阵RHHp维数高达1 200×400，直接进行频域LMMSE计算复杂度十分高，因而对矩阵采用滑动窗[14-15]的方法来简化运算，减小存储空间。导频子载波之间相关性的强弱与它们相隔的间距有关，距离越近，相关性则越强，因此可以仅利用当前子载波距离较近强相关的导频响应值来进行数据子载波估计，而不是所有的导频信号，这样可以大幅度减小计算量。

以100个RB为例，描述LMMSE滑动窗的算法原理，如图4所示，图中R表示导频子载波，R′表示虚拟导频子载波，阴影部分表示每次滑窗口时利用的导频子载波。采用3个RB为单位进行滤波，也就是12个导频子载波，下一次滑动3个子载波，即滑动一个导频子载波，每次滤波输出取中间3个子载波,则在本文使用的100个资源块的情况下，需进行388次滑窗，开始的18个子载波和最后的18个子载波则用原来的方法滤波，作单独的处理。因而自相关矩阵RHpHp的维数降至12×12，互相关矩阵RHHp的维数降至36×12，实现了降低复杂度的目的。

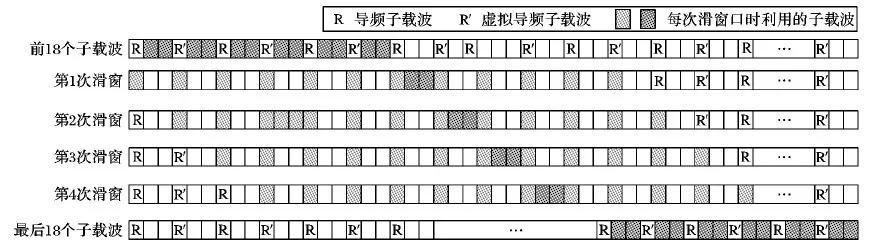
图4 LMMSE滑动窗示意图

1.3 时域线性插值

相关时间内，信道时域变化可认为十分缓慢，而且时域插值需要接收大量数据，衡量算法性能和运算复杂度，采用线性内插，因此在频域LMMSE滤波计算后，在时域进行线性插值，线性插值算法的基本原理是利用相邻参考信号位置的信道频率相应值，得到数据位置的信道频率相应值。

时域线性插值算法公式为：

(17)

其中：HLMMSE(k,l1)、HLMMSE(k,l2)分别对应相同频域位置不同时域位置上的参考信号的信道响应值。

1.4 改进算法整体步骤

改进的基于CRS信道估计算法的整体实现步骤如下：

步骤1 根据小区参考信号映射规则对所有接收信号进行导频抽取得到CRS处的接收信号，利用接收信号与本地导频信号完成LS估计。

步骤2 由已得到的导频信道LS估计值进行插值，相当于增加虚拟导频，从而将导频加倍。

步骤3 通过对信道时延参数和信噪比进行估计，从LMMSE频域插值矩阵存储单元中选择相应的插值矩阵W。

步骤4 频域插值读取W矩阵，利用频域滑动窗算法根据HLMMSE=WHLS估计出含导频的OFDM符号信道估计值。

步骤5 进行时域线性插值，得到全部子载波的信道响应估计值。

其总体流程如图5所示。

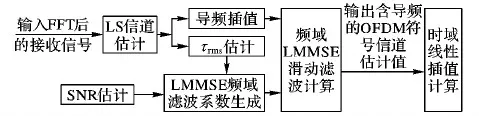
图5 基于CRS的信道估计方案

2 仿真结果及分析

2.1 复杂度分析

在实际应用中，计算复杂度是决定工程成本的一个关键性因素。假设一个OFDM符号上有NP个导频，改进算法可将传统LMMSE算法的复杂度从O(NP3)降至O(NP)。在增加虚拟导频以及资源块为100个的情况下，所提改进LMMSE插值算法的应用可将相关矩阵求逆的维数从400×400降至12×12，矩阵复数乘法和加法的运算次数也大幅度降低，其中比传统LMMSE插值算法运算次数降低了98.67%，比目前成熟的基于奇异值分解(SVD)的LMMSE算法运算次数降低了42.49%，并且，本文提出的改进算法的运行时间显然少于传统LMMSE算法以及基于奇异值分解的LMMSE算法，具体运算复杂度如表2所示。

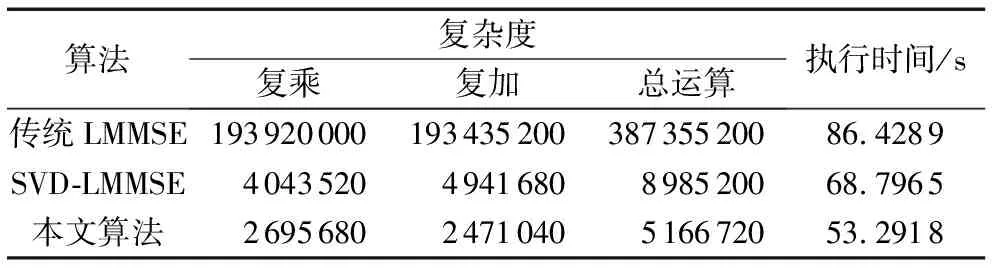
表2 算法运算复杂度及运行时间比较

2.2 性能分析

为了验证本文算法的性能，在导频子载波位置处均利用LS信道估计算法，在时域上采用相同的内插算法即线性插值，在频域上则分别使用多种不同的插值算法，在误码率(Bit Error Rate, BER)和均方误差(Mean Squared Error, MSE)两方面进行性能比较。此外，本文仿真时假设系统理想同步，即接收端和发送端完全同步。所使用的仿真配置如表3所示。

表3 仿真参数

图6(a)给出了当天线采用一发四收时，在不同的插值算法下系统误码率的比较。其中：LINEAR表示线性插值算法；DFT表示基于DFT的插值算法；LMMSE表示理想LMMSE插值算法；IM-LMMSE曲线表示本文改进的LMMSE插值算法性能；NO-WINDOW表示本文改进算法不使用滑动窗；SVD-LMMSE表示基于奇异值分解的LMMSE算法，并以理想信道频率响应下的误码率性能曲线作为参考，用PERFECT表示理想信道下的性能曲线。

从图6(a)中可以看出，在信道二阶统计特性未知的情况下，改进插值算法的BER性能要优于线性插值算法和基于DFT的插值算法以及目前较为流行的基于奇异值分解的LMMSE(SVD-LMMSE)算法。最接近理想信道BER性能的是理想LMMSE特性曲线，改进的LMMSE插值算法性能相对于传统的LMMSE算法和不加滑动窗时的性能损失很小。由于改进算法可以实时估计信道时延参数，因此在SNR较小的条件下，误码率仍较低，且与理想状态下的LMMSE插值算法非常接近。

图6(b)为在一发四收的场景下不同插值算法的MSE性能对比，可以看出，当SNR相同时，改进LMMSE插值算法的MSE性能明显优于其他几种插值算法，在SNR大于15 dB时，改进LMMSE插值算法可有效逼近理想LMMSE特性曲线。所提算法不加滑动窗时(“NO-WINDOW”曲线)的MSE性能略优于加窗的，但由表2可知，滑动窗的使用可大幅度降低算法复杂度。

图7为使用本文提出的算法得到的接收端64QAM星座图，可看出星座图毛刺现象很少，星座图没有发生畸变，由此表明本文所提信道算法可以较好改善信号传输质量，从而降低系统传输误码率。

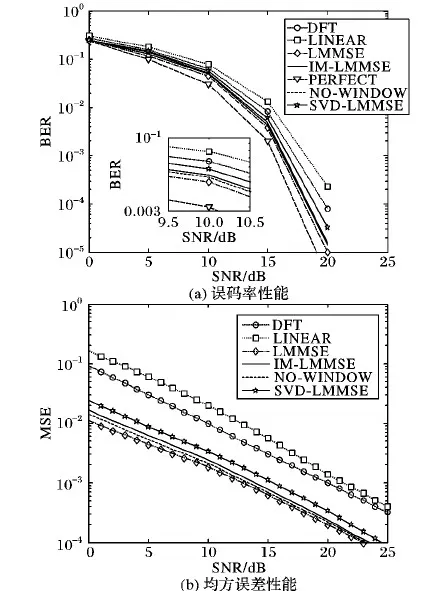
图6 不同插值算法一发四收的不同性能对比

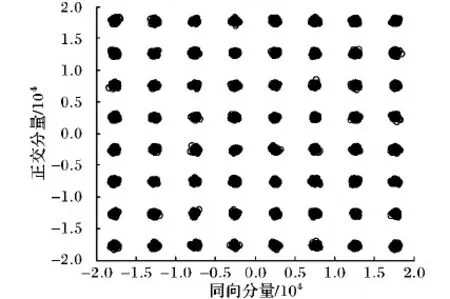
图7 本文算法一发四收下的64QAM接收星座图

最后为了验证算法在其他收发天线的有效性，在四发四收的条件下对不同插值算法进行了误码率性能比较，同样从图8可看出，改进算法的BER仍然明显优于线性插值与DFT插值，从而说明了改进插值LMSME算法的整体性能较好。

3 结语

LMMSE插值算法的实现需要信道先验信息，但是实际环境中往往无法提前获取，且矩阵实时求逆运算量大。针对上述问题，本文对信道时延参数和信噪比进行有效估计，进而选取与当前信道最为匹配的频域滤波矩阵，解决了传统LMMSE算法造成的信道函数失配问题。仿真结果表明，所提算法性能较好，与传统LMMSE算法相比，该算法无需提前获取信道统计特性，此外滑动窗的使用有效降低了运算复杂度，提升了系统运算效率。该算法简单可行，达到了提高实用性和性能的目的，适用于实际工程应用。另外，实际系统并非完全同步，所提算法建立在理想同步的条件下，与实际情况有偏差，因此频偏下的信道估计方案设计将是下一步的研究重点。

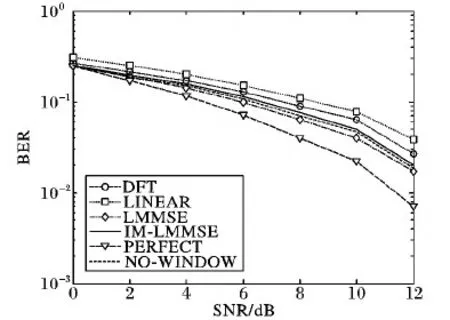
图8 四发四收下不同算法的误码率性能对比