基于分段降维和路径修正DTW的时序特征分类器设计

常炳国，臧虹颖

(湖南大学 信息科学与工程学院，长沙 410082)(*通信作者电子邮箱657475865@qq.com)

0 引言

当前，时间序列的分类和聚类研究正受到越来越多的关注，在图像识别、信号处理、生物信息识别以及金融等领域得到广泛应用。相似性度量作为时间序列挖掘工作的基础步骤，其运算效率以及准确率直接影响时间序列挖掘的最终效果[1]。动态时间弯曲(Dynamic Time Warping， DTW)方法的提出最初是为了解决语音序列长短不一的模板匹配问题，逐渐被应用到不等长时间序列的相似性度量当中[2]。DTW度量允许数据点之间“一对多”的映射，通过动态规划查找数据点之间的最佳匹配路径，以实现数据在时间轴上的伸缩变化。由于其概念简单、准确率高、鲁棒性强等优点，已成为相似性度量中最常用的距离度量方法之一。针对DTW计算复杂度高、算法效率低等局限，Mei等[3]提出了基于Mahalanobis距离的DTW度量方法，该方法先利用马氏距离建立了每个变量和类别之间的准确对应关系；然后再通过DTW对齐时间上不同步的序列。Sharabiani等[4]提出新的逼近方法来减小DTW输入序列的长度，以此提高DTW搜索效率，他将该种降维方法命名为控制图近似法(Control Chart Approximation， CCA)。Sun等[5]提出了一种全局约束度下的修剪动态规划方法，从理论上证明了带有全局约束的DTW匹配路径对于度量修剪策略的有效性，并证明用它能得到序列之间近似最优解。李正欣等[6]在Keogh构造的下界距离，记为LB_Keogh[7]的基础上，提出了一种支持DTW距离的多元时间序列的索引结构，并设计了早停机制以减少计算代价。李海林等[8]结合数值导数构造了新的特征序列，并设计了符合该特征序列的度量函数。综合来看，现阶段的研究主要从降低时间序列维度、制定全局约束条件以及设计新的下界函数三个方面展开[9]，以改善动态时间弯曲度量性能。

针对DTW方法仅关注路径累积距离最短而出现过度弯曲现象，无法准确选择最优弯曲路径，进而影响时间序列分类和聚类准确率的问题，本文提出一种基于路径修正的动态时间弯曲(Updated Dynamic Time Warping， UDTW)距离度量方法，通过给弯曲路径设置惩罚系数，实现了对DTW弯曲变化率的动态调整，有利于从多条序列中选出形态相似的弯曲路径。在进行UDTW距离度量之前，利用改进过的分段聚集近似(Piecewise Aggregate Approximation， PAA)方法提取原始时间序列的特征，以降低DTW计算代价，从而整体上提高时间序列相似性度量的效率和准确率。

1 时序特征提取

假定一条时间序列S的长度为m：S={s1,s2,…,si,…,sm}，另一条时间序列T的长度为n：T={t1,t2,…,tj,…,tn}。创建一个m×n的距离矩阵D，用d(ith,jth)表示(si,tj)两点的路径距离：d(i,j)=‖si-tj‖p，其中‖x‖p表示p-范数。计算DTW距离时，先构造一个累积距离矩阵R，R中对应元素γ(ith,jth)定义为：

γ(i,j)=d(i,j)+min {γ(i-1,j),

γ(i-1,j-1),γ(i,j-1)}

(1)

计算时，按照行(或列)的方向依次计算γ(i,j)的值，最后求得γ(m,n)即为序列S、T的DTW距离。由于对R中每一个元素进行了计算，DTW度量方法的时间复杂度为O(m×n)。由此可见，如果能够缩短时间序列S、T的长度，便能大幅度减少DTW的计算代价。

常用的特征提取的方法有分段线性近似(Piecewise Linear Approximation， PLA)[10]，利用最小二乘法求得分段序列的最佳线性拟合曲线，该方法能较好地还原原始序列的形态，但对于长度为m，分段数目为L的序列来说，时间复杂度高达O(m2L)。类似的方法还有分段多项式表示(Piecewise Polynomial Representation， PPR)、分段回归近似(Piecewise Regression Approximation， PRA)和自适应分段常量近似(Adaptive Piecewise Constant Approximation， APCA)等，虽然这些方法都对序列作了分段处理以达到降维目的，但这些方法本身时间复杂度较高，算法效率较低[11]。

分段聚合近似(PAA)用等长度窗口分割时间序列，每个窗口内序列特征用窗口的平均值来表示。

定义1 PAA。将时间序列S={s1,s2,…,si,…,sm}分为L段的PAA模型表示为：

SPAA={AVG(S1′),AVG(S2′),…,AVG(Sl′)};

l=1,2,…,L

(2)

其中AVG(Sl′)表示第l个窗口内数据子集Sl′的均值，窗口长度w=m/L(或m/L+1)。通过将每段的均值数据相连接形成新序列SPAA，从而实现数据降维的目的。PAA具有概念简单、参数少(仅只有一个参数L)、时间复杂度低等优点，是一种有效的特征提取方法，但它仅反映了序列整体的变化趋势，而忽略了时间序列的形态特征，并且，PAA对均值平稳的独立噪声数据不敏感，存在重要数据点或异常数据点信息丢失的不足[12]。综合考虑PAA的优缺点，本文采用窗口最大值代替平均值的数据提取策略，然后用分段平均值对最大值进行适度平滑处理以消除噪声影响，本文将此种方法称为分段局部最大值平滑法(Piecewise Local Max-smoothing， PLM)。

定义2 PLM。将时间序列S={s1,s2,…,si,…,sm}分为L段的PLM模型表示为：

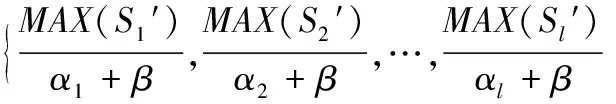
l=1,2,…,L

(3)

用αl=MAX(Sl′)-AVG(Sl′)表示第l个窗口最大值与平均值的差值，β为平滑常数，用于调整数据的变化范围，由于前期对序列作了Z-score规范化处理，β取1即可。图1给出了长度为48的序列S分别经过PLM和PAA方法提取特征值后所形成的特征序列SPLM、SPAA，此处窗口长度w=6。

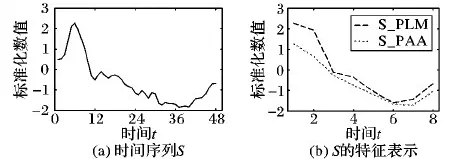
图1 时间序列S及其特征表示举例

PLM方法只需一次遍历序列即可完成特征提取，时间复杂度为O(m)，与PAA相比，PLM能更好地提取数据的形态特征，保留了主要的趋势转折点数据，同时适度的平滑处理消除了部分异常噪声数据的影响，增强了对异常数据的容错能力。

2 修正算法

与欧氏距离(Euclidean)度量方法[13]相比，DTW方法解决了时间点不对齐、形态之间伸缩、扩展的问题，但是DTW在选择最优路径时，为了达到累积距离最短，可能会出现多个点对应到同一点的现象，最终选择出一条在垂直方向或水平方向过度复制的弯曲路径。图2(a)描述了序列A与序列B经过DTW度量后产生的最短弯曲路径距离为5.09；图2(b)给出了序列A与序列B对应的点对点匹配关系；图2(c)描述了序列A与序列C经过DTW度量后产生的最短弯曲路径距离为5.12；图2(d)给出了序列A与序列C对应的点对点匹配关系。在进行相似性度量时，由于序列B与序列A的DTW距离更短，往往会把序列B匹配到序列A所在类别，尽管从形态上看，序列C的变化趋势更符合序列A的特征。在图像检索、模式识别等领域内，序列模式形态的相似性是匹配成功与否的一个重要标准，而DTW度量方法仅仅只基于弯曲距离最短这一限制，极有可能错失正确的分类。

2.1 惩罚函数

两个时间序列之间最理想的对应关系应该是相同特征之间的一一对应，比如一条时间序列上的波峰应与另一条序列的波峰对应，而不是波谷。DTW度量在选择最优弯曲路径时，仅仅只考虑了累积距离最短，没有对其弯曲的步数进行一定的限制，从而忽略了形态相似性的重要性，因此，给过度弯曲的路径设置一定的惩罚系数是有必要的，对于在路径的垂直和水平方向连续转移的步数，要以一定的增长率逐渐增加其惩罚系数，达到约束其弯曲路径的目的。理想的惩罚函数q(x)应满足以下三个条件：

1)有界性。q(0)=0，qmax为常数，即最小惩罚系数为0(不惩罚)，最大的惩罚系数可控。

2)单调性。n-m≥0 ⟹q(n)-q(m)≥0。随着连续弯曲步数的增大，惩罚系数也要逐渐增大。

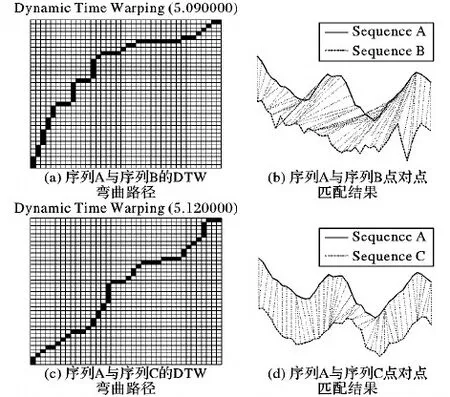
图2 弯曲路径与点对点匹配结果

为了满足以上3个条件，本文定义惩罚函数为：

q(x)=-qmax(cos(πx/2μ)-1);x∈(0,μ)

(4)

其中：qmax为惩罚函数的上界值，可以根据需要进行调整；μ为达到上界值对应的最大弯曲步数，也是算法允许在同一方向连续转移的最大弯曲步数，q(μ)=qmax。图3给出了上界值qmax=10时不同μ值对应惩罚函数曲线，μ值越大，曲线越平缓，则度量时允许连续弯曲的步数越多。最大弯曲步数μ是一个经验值，通过设定μ值的大小来控制惩罚函数的倾斜度，实现对惩罚系数的动态调整。

图3 不同μ值对应的惩罚函数q(x)

2.2 修正动态弯曲距离

假定时间序列S的长度为m：S={s1,s2,…,si,…,sm}，时间序列T的长度为n：T={t1,t2,…,tj,…,tn}。基于惩罚函数计算动态弯曲距离时，采用计数矩阵A记录时间序列S上每个数据点在水平和垂直方向连续转移的步数，计数矩阵B记录时间序列T的数据点连续转移的步数。UDTW的计算步骤如下：

步骤1 初始化计数矩阵A=(ai)1×m和B=(bj)1×n，A与B初始化为零矩阵。

步骤2 计算时间序列S与T之间的距离矩阵D=(dij)m×n，其中dij=d(i,j)=|si-tj|。

步骤3 计算累积距离矩阵R=(γij)m×n中第1行数据γ(s1,T)以及第1列数据γ(S,t1)。

步骤4 按照行(或列)的方向依次求解其他γ(i,j)的值，同时，当路径更新到γ(i,j)时，记录下当前点si和tj被使用的次数，并更新计数矩阵ai和bj的值。在计算γ(i,j)时，按照如下公式求解：

γ(i,j)=min {c(bj)×d(i,j)+γ(i-1,j),d(i,j)+

γ(i-1,j-1),c(aj)×d(i,j)+γ(i,j-1)}

(5)

其中

(6)

步骤5 重复执行步骤4，直至求得修正动态弯曲距离UDTW(S,T)=γ(m,n)。

算法1中给出了UDTW中生成计数矩阵和距离矩阵的伪代码。

算法1 GENMATRIX(S,T)。

输入：时间序列S、T。

输出：计数矩阵A、B，距离矩阵D。

m=len(S),n=len(T)

A=zeros(m),B=zeros(n)

fori=1:m

forj=1:n

d(i,j)=|si-tj|

returnA、B、D

算法2中给出了求解修正动态弯曲距离的伪代码。

算法2 GENUDTW(A,B,D,q(x))。

输入：计数矩阵A、B，距离矩阵D，惩罚函数q(x)；

输出：修正动态弯曲距离UDTW(S,T)。

fori=1:m

R(i,1)=c(B[1])×d(i,1)+R(i-1,1)

B[1]=B[1]+1,A[i]=A[i]+1

forj=1:n

R(1,j)=c(A[1])×d(1,j)+R(1,j-1)

A[1]=A[1]+1,B[j]=B[j]+1

forj=2:n

fori=2:m

T1=c(B[j])×d(i,j)+R(i-1,j)

T1=d(i,j)+R(i-1,j-1)

T3=c(A[i])×d(i,j)+R(i,j-1)

Index,R(i,j)=MIN{T1,T2,T3}

IfIndex=0:B[j]=B[j]+1,A[i]+1

elseifIndex=2:A[i]=A[i]+1,B[j]=1

elseA[i]=1,B[j]=1

returnR(m,n)

2.3 时间复杂度分析

本文所提出方法是在PLM的基础上使用UDTW度量方法，因此可简记为PLM-UDTW(Piecewise Local Max-smoothing-Updated Time Dynamic Warping)。首先通过PLM方法对序列进行特征提取，将长度为m的序列压缩成长度为L的短序列，此处时间复杂度为O(m)。对降维后的序列作UDTW度量时增加了一个更新计数矩阵的操作，但该操作并没有增加其时间复杂度，因此，对两条长度为m的序列作UDTW度量的时间复杂度为O(2m+L2)，当压缩率(m/L)为10%，m=128时，PLM-UDTW的时间复杂度降低了97.4%。

3 实验研究与分析

采用来自UCR[14]时间序列数据集，经过Z-scores(均值为0、方差为1)规范化处理。运用本文提出的修正算法进行实验分析并验证其有效性。数据集分成训练集和测试集两部分，采用“1-近邻”分类方法，运用训练集学习生成分类器，运用测试集验证分类器的准确率。本文算法均使用Python 3.6代码实现。

3.1 分段特征提取

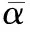
(7)

β=max{α2,α3,…,αi,…,α20}

(8)

此处wmax=20，αi是当窗口长度w=i时算法对应的分类准确率。表1给出了15个时间序列数据集的相关信息，其中I.P.D(ItalyPowerDemand)、M.I(MedicalImages)、T.L.ECG(TwoLeadECG)为对应数据集的缩写模式。

表1 时间序列数据集信息

通过表2结果可以看出，PLM方法在Computers、ECG、Face(four)、Gun-Poin、tLightning- 7、M.I、OliveOil、T.L.ECG这8个数据集上的平均分类准确率和最高准确率均高于PAA方法，在Beef、Coffee、Lightning- 2、Trace这4个数据集上最高分类准确率与PAA方法相同，但平均分类准确率比PAA方法高。证明与PAA方法相比，PLM方法至少可以提高12个数据集上的分类准确率。为了进一步说明PAA方法和PLM方法在具体数据集上的表现，图4给出了Gun-Point数据集在不同窗口长度下分类准确率的变化情况。通过观察可得，随着窗口长度的增大，经过PAA方法提取特征后的数据分类准确率逐渐降低，而PLM方法提取特征后的分类准确率在一定范围内上下波动，当窗口长度w=20时(压缩率为5%)，PLM方法的分类准确率依然保持约90.67%，远高于PAA方法的78.67%。实验结果说明，PLM方法具有更好的鲁棒性，其对窗口长度的依赖性更小。与PAA方法相比，在未增加时间复杂度的基础上具有更好的特征提取效果。

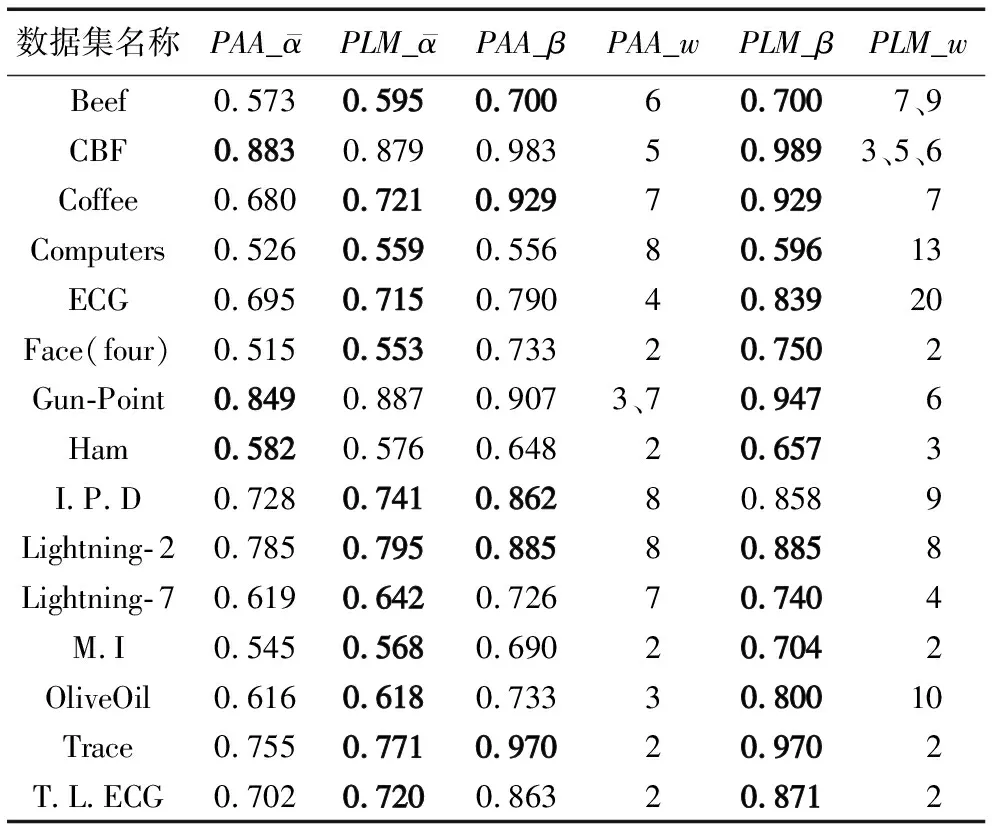
表2 PAA与PLM方法分类准确率对比

图4 Gun-Point数据集不同窗口长度w下的分类准确率对比

另外，通过对表2结果分析可得，最佳窗口长度大多集中在2～10，即当压缩率范围为50%～10%，分段特征提取方法能取得较好效果。

3.2 UDTW度量效果

UDTW中的惩罚函数控制了动态弯曲路径的修正程度，有两个重要参数对分类效果产生直接影响：一个是惩罚系数的上界值qmax，决定了最大惩罚系数；一个是达到上界值所对应的最大弯曲步数μ。由于这两个参数都是对惩罚函数的倾斜度作调整，且上界值对所有弯曲路径是同一标度下的，因此可将qmax固定为1。实验通过调整μ值大小验证UDTW算法的分类效果。图5给出了μ值在[0,10]区间变化时，上述15个数据集分类准确率的波动情况。为提高UDTW计算效率，实验先采用PLM方法对时间序列进行特征提取，此处窗口长度设置为w=7。

参数μ的调整实际是在欧氏距离和DTW距离之间找到一个最优平衡，当μ=0时，UDTW距离向欧氏距离靠近，当μ足够大时，UDTW距离无限逼近DTW距离。针对不同数据集，达到最佳分类准确率的μ值有所不同，说明不同数据集对时间序列形态特征的关注度有所不同。例如数据集ECG的最优参数为μ=0，在该参数下达到最高分类准确率91%，这说明对ECG数据集的分类更关注数据的形态特征，因此倾向于用欧氏距离进行相似性度量；文献[15]也证明了这一观点，即对于ECG数据集来说，欧氏距离作为度量距离能取得更好的分类效果。随着μ值增大，同一数据集的分类准确率会呈现一定的波动，但对于I.P.D、M.I等数据集，分类准确率没有明显变化，经过分析发现原因在于原始序列长度较短，在分段特征提取之后保留的形态特征过少，因此对于这些数据集来说，一个解决的方法是减小特征提取的窗口长度，或者不作分段降维处理。

图5 15个数据集的不同μ值下的分类准确率对比

进一步，为了说明PLM-UDTW的有效性，选择欧氏距离、DTW、导数动态弯曲距离(Derivative Dynamic Time Warping， DDTW)[15]、PLM-UDTW四种距离度量方法，采用1-近邻分类方法直接对上述15个数据集进行分类，表3给出了4种算法在每一数据集下的分类错误率，由于PLM-UDTW对序列进行了分段处理，因此给出达到该分类错误率下的一种窗口长度w和对应的最大弯曲步数μ。错误率的计算公式如下：

Errorrate=测试集中分类错误的个数/测试集大小

(9)

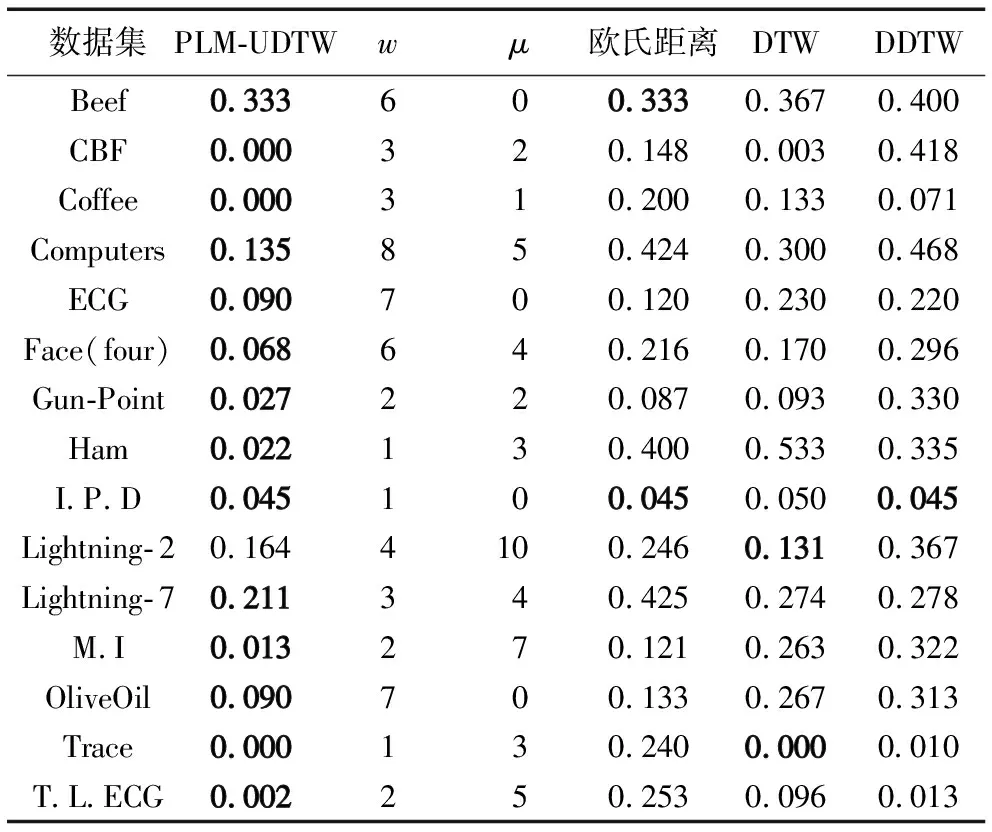
表3 PLM-UDTW与传统度量方法的错误率对比

从表3中可以看出：PLM-UDTW方法在CBF、Coffee、Trace这3个数据集上错误率为0，即达到了100%分类正确；在Beef、Computers、ECG等14个数据集上分类准确率均为4种方法中最高；在Lightning- 2数据集上准确率仅次于DTW方法。与DDTW度量方法相比，PLM-UDTW在CBF、Computers、Ham三个数据集上准确率分别提高了71.8%、62.6%和47.07%，在15个数据集上准确率平均提高了27.7%。与欧氏距离度量方法和传统DTW度量方法相比，PLM-UDTW的分类准确率也有显著提高，最高分别提升了65.7%和109.4%；在15个数据集上准确率平均提高了21%和17.7%，进而证明了本文方法在时间序列分类中的有效性和优越性。

3.3 计算时间开销

根据2.3节描述，分段降维方法能有效降低UDTW的时间复杂度。将时间序列的分类算法分成三个操作过程：1)分段降维过程；2)测试集、训练集距离度量过程；3)1-近邻(1-Nearest Neighbor, 1-NN)分类过程。表4给出ECG数据集在UDTW、DTW、DDTW三种度量方法下的时间开销。

表4 3种算法的平均运行时间对比 s

根据表4分析，DDTW运行时间最长，这是因为DDTW方法比DTW方法增加了一个求数值导数的操作。运行时间最短的是UDTW，尽管与传统DTW和DDTW方法相比新增加了一个分段降维过程，但是算法消耗的总时间减少了很大比例，这个比例主要依赖于窗口长度w。当w=7时(压缩率约为14%)，耗时约减少99%。综上所述，PLM方法能有效降低时序特征分类算法的时间复杂度，与DTW、DDTW方法相比，PLM-UDTW在不影响分类准确率的前提下极大地提高了计算效率。

4 结语

本文提出了一种基于路径修正的DTW(UDTW)度量方法，解决了DTW易陷入过度弯曲而忽略时间序列形态相似性的问题。通过对原始序列进行分段特征提取降低了DTW度量的计算代价，提高了算法的整体效率；同时，对PAA分段降维方法作了改进，使其能更好地提取时间序列的曲线形态特征。实验结果表明，PLM-UDTW算法可以提高15个时间序列数据集中大部分数据集分类准确率，并明显提高分类速度。