补偿目标机动和制导动力学的制导律

李富贵,贾生伟，2,卜奎晨,高 峰,佟泽友

(1.中国运载火箭技术研究院， 北京 100076; 2.南京航空航天大学， 南京 210016)

当前战场环境日趋复杂，导弹飞行过程中面临复杂的对抗环境[1]。诸如主动隐身、电磁干扰、目标机动等给导弹的作战效能来了极为不利的影响。如何在高对抗条件下，提高制导性能是当前迫切需要解决的问题[2]。

制导律是制导系统的重要组成部分，对制导性能的有关键作用。使用先进的制导律是改善制导性能的重要措施。高对抗环境下，导引头捕获目标的作用距离严重下降，造成末制导段的飞行时间严重压缩；同时目标在末制导段的机动会引起更大的需用过载[3]。

当前有部分学者对此问题进行了研究，取得了一些成果，但总体来说，工程实现难度较大。本文研究了一种制导律，通过制导动力学的补偿，缩短了末制导段的需用时间，通过目标机动补偿，降低了导弹需用过载，可以实现高对抗条件下的使用。时域和频域等效方法，可实现对制导动力学的补偿修正。

1 制导律模型与求解

制导律求解用的模型常为线性化模型，以便于利用最优化方法推导出最优解，且模型的复杂度不宜高，否则给求解和实际工程应用将带来巨大的困难[4]。制导动力学包括导弹的动力学和目标的动力学。设导弹动力学模型为

(1)

式(1)中:amc为导弹加速度指令；am为导弹加速度响应； 1/ωm为弹体动力学时间常数。

目标动力学模型为

(2)

式(2)中:atc为目标加速度指令;am为目标加速度响应; 1/ωt为目标动力学时间常数。

(3)

取目标函数为命中时刻脱靶量为零且控制能量最小，即

(4)

式(4)中tF为末制导时间。式(3)对应改写为

(5)

设t为时间，则有：

Φ(t)=L-1[(sI-A)-1]

(6)

则式(5)微分方程的的解为：

(7)

在式(7)中只取第一个状态量，则有：

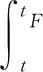
(8)

令剩余飞行时间tgo=tF-t，则式(8)中：

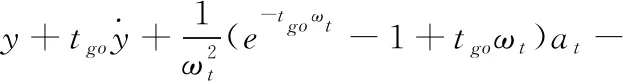
(9)

(10)

把终端条件y(tF)=0代入式(9)，可得：

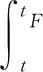
(11)

由柯西不等式有：

(12)

当等号成立时，所需控制能量最小，则由柯西不等式等号成立的条件有：

amc(λ)=kh1(tF-λ)

(13)

把式(13)代入式(12)，可得

(14)

设弹目视线角为q，弹目接近速度为Vc，小角条件下有：

(15)

对式(15)求导得：

(16)

把式(9)、式(10)、式(14)、式(16)代入式(13)后，经过化简可得最优制导律：

(17)

令：

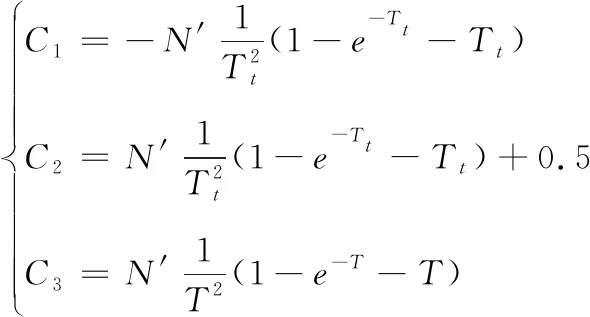
(18)

则最优制导律可表示为

(19)

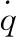
2 制导动力学时间常数等效方法

为使制导律的形式及使用简单，最优制导律推导时假设导弹和目标的动力学均为一阶滞后模型。而实际上导弹和目标的动力学特性是复杂的高阶动力学特性。如何把这诸多的复杂动力学等效为制导律中需用的一阶动力学，以维持最优制导律性能不下降太多是最优制导律应用中须解决的问题。

动力学时间常数可以使用时域或频域特征点进行等效。对于一阶系统t63特征(系统阶跃响应上升到终值63%的时间)即为系统时间常数，对于高价系统也可以系统阶跃响应获得t63指标用于等效时间常数。系统带宽ωb是重要的频域特征点，对于一阶系统，1/ωb即为系统时间常数。

为了对比在不同阶数时ωb和t63等效策略，需要在不同阶数的制导动力学下研究等效后制导律的性能。一个很好的方法是把系统时间常数和系统阶数的影响分开，采用一个多项式动力学系统[4]：

(20)

其中n为系统阶数。

在文献[4]中T也常被取近似为制导系统时间常数，在T=1时，不同阶数n下由t63和ωb计算得到的等效时间常数如表1所示。

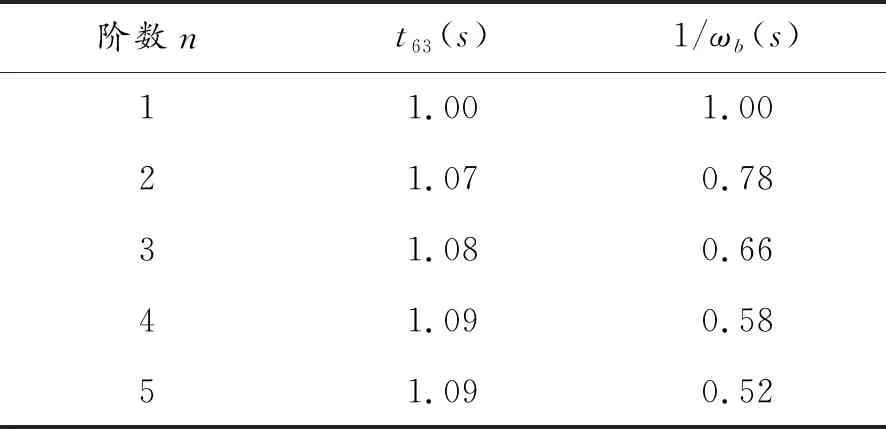
表1 不同阶数下等效时间常数

由上述计算结果可知T≈t63，而随着阶数增加，1/ωb与t63相差越大，当系统为5阶时，两种等效策略得到的时间常数相差1倍。

3 最优制导律性能

最优制导律正向分析模型如图2所示，图中Vm为导弹速度，HE为初始指向偏差角。

取目标机动加速度指令atc=4g，制导时间常数1/ωm=1 s，1/ωt=1 s，飞行时间为10 s。在制导信息理想的条件下本最优制导律(OPN)和比例导引律(PN)[6]及增强比例导引律(APN)[6]的需用加速度指令值如图3所示。

从图3可知，最优制导律加速度曲线为一条直线，末段过载收敛为0，这说明最优制导律正好消除了系统动力学，同时完全补偿了目标机动和重力加速度的影响。比例导引律和增强比例导引律制导律在末端需用加速度极大。

定义无量纲参数：

对图2进行无量纲化，并运用伴随函数法[7]，可得到无量纲伴随函数框图，如图4所示。图4给出了在初始指向偏差和目标机动条件下的无量纲伴随函数框图，其中制导系数也进行了无量纲伴随处理。

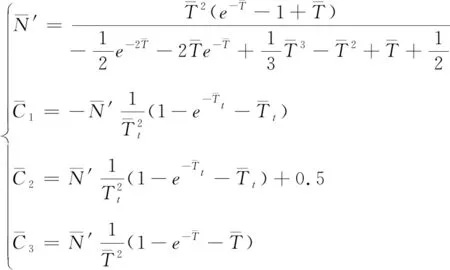
(21)

在初始指向偏差下，图5给出了比例制导律在不同阶数制导动力学下无量纲脱靶量随无量纲末导时间变化曲线，当末制导时间大于10倍的制导动力学时间常数时，初始指向偏差引起的脱靶量才会归零。同样，也可得到初始指向偏差干扰下最优制导律无量纲脱靶量随无量纲末导时间变化曲线，图6中制导系统时间常数等于t63，图7中制导系统时间常数取为1/ωb，当末制导时间大于4～6倍的制导动力学时间常数时，脱靶量会归零。

同理，在目标机动下，图8给出了比例制导律无量纲脱靶量随无量纲末导时间变化曲线，当末制导时间大于10倍的制导动力学时间常数时，目标机动引起的脱靶量才会逐渐趋于零。最优制导律下无量纲脱靶量随无量纲末导时间变化曲线如图9和图10所示。其中图9中制导系统时间常数等于t63，图10中制导系统时间常数取为1/ωb，当末制导时间大于6倍的制导动力学时间常数时，目标机动引起的脱靶量会归零。

综上可知，对于最优制导律制导动力学时间常数取t63还是1/ωb均可获得不错的效果，虽然高阶动力学条件下两种等效策略得到的时间常数相差近一倍，反映了最优制导律对制导动力学时间常数的鲁棒性非常好，在工程中两种制导时间常数等效策略都可以使用。最优制导律不仅减小了需用过载，而且使得所需末制导时间缩小为比例导引律的60%，这较大降低了对导引头探测距离和导弹末端机动过载的需求，对于隐身目标、大机动目标具有非常重要的意义。

4 结论

该制导律可有效降低导弹需用过载，制导末端需用过载收敛为零；该制导律有效降低了需用末制导时间，末制导时间需要6倍的制导时间常数，是比例导引律需用末制导时间的60%；最优制导律对制导系统动力学时间常数修正值具有很强的鲁棒性，时域指标t63或频域指标1/ωb均可作为修正用的制导动力学时间常数。