引信误差对空炸榴弹散布及作战效能的影响

2018-08-27庞春桥任保祥李智宇王小峰

兵器装备工程学报 2018年12期

庞春桥，陶钢，闻鹏，任保祥，李智宇，王小峰

(南京理工大学能源与动力工程学院，南京 210094)

单兵榴弹作为班组作战的主力弹种，其主要战斗任务之一是面杀伤敌方有生力量，为了提高单兵榴弹面杀伤效果，一般采取空炸的模式[1]。在以往的研究中，研究人员往往将射击效率和目标毁伤效率分开研究。文献[2-3]中采用蒙特卡罗方法进行了弹丸模拟打靶研究；文献[4-5]中进行了不同形式的非接触式弹药的杀伤概率计算；然而以上研究是分开独立进行的，很难给出弹丸实际作战效能。在引信的研究方面，目前研究人员最关注的是如何提高引信的精度以及先进引战配合系统设计[6-7]，这在接触式毁伤弹药和防空反导弹药[7]的设计中是很重要的，然而对于单兵空炸榴弹而言，时间引信的精度并非越高越好，这主要是由单兵空炸榴弹的作战使命决定的。因此，引信的选择需要根据弹丸性质及其需要完成的作战使命来确定。

本文首先从外弹道及作战时的射击方法出发，采用蒙特卡洛方法对典型目标距离(300 m，500 m，800 m)进行模拟打靶，得到了时间引信误差对单兵空炸榴弹空间散布规律的影响。然后将射击效率与坐标毁伤定律相结合，给出了非接触式毁伤弹药作战效能的简单计算模型。最后进行了算例分析，得到了时间引信误差对单兵空炸榴弹作战效能的影响。

1 外弹道方程的建立

1.1 气象条件

本文选用我国炮兵标准气象条件[8]，其地面值为：

(1)

在对流层(y≤9 300 m)温度随高度的标准定律为：

τ=τ0n-6.328×10-3y

(2)

气压随高度变化的标准定律为：

(3)

空气密度随高度变化的标准定律为：

H(y)=ρ/ρ0n=π(y)τ0n/τ

(4)

在计算过程中有以下经验公式：

H(y)=e-1.059×10-4y

(5)

1.2 空气阻力函数

弹丸的空气阻力加速度ax应为

ax=Rx/m=gRx/G

(6)

其中：m为弹丸的质量;G为弹重。将空气阻力以阻力系数形式代入式(6)，得

cH(y)F(v)cH(y)vG(v)

(7)

4.737×10-4v2Cxon(M)

若记F(v)=vG(v)=v2K(v)，则有

这里F(v)，G(v)，K(v)统称为阻力函数。从表达式不难看阻力函数不仅是速度v，而且是音速C的函数，对于不同的阻力定律，对应的阻力函数也不相同，本文采用43年阻力定律(见图1)。

1.3 弹丸质心运动方程组

在直角坐标系中，弹丸质心运动方程组可表示为：

(8)

初始条件：t=0时

vx=v0cosφ0cosθ0,vy=v0cosφ0sinθ0,

vz=v0sinφ0，x=0,y=0,z=0

1.4 计算参量及计算方法

弹丸直径：d=82 mm；弹丸质量：m=2.3 kg；弹丸初速：v=255 m/s；弹形系数：i=1.2。

在确定初始值之后，对上述方程组联立采用四阶Runge-Kutta法求解。对于一般情况有s个微分方程组和t个代数方程组，变量则共有s+t个。在这s+t个变量中，第s+1，…，s+t个变量可以表示成第1，…，s个变量的函数，所以仍可以归结为s个变量s个微分方程的求解问题，即

(9)

取步长h=xn+1-xn，如果已知xn,yin，可以用以下公式确定xn+1时的yi,n+1,i=1,2,…,s。

i=1,2,…,s

(10)

其中

i=1,2,…,s

这样，就可以求出整个外弹道飞行过程中各参数随时间的变化规律。

值得注意的是外弹道方程计算的准确性是后文模拟打靶的基础，在进行模拟打靶之前首先需要对外弹道程序进行试验符合。为此分别针对400 m和500 m射程进行了外弹道试验，并将实际初速作为初始条件，实际射程作为截至条件代入上述程序计算弹丸飞行时间，与高速录像记录的实际飞行时间相比，误差在0.5%以下，程序计算结果与试验结果具有很好的一致性，可以保证外弹道计算的精度。

1.5 外弹道计算结果

为了方便射手在战场环境下快速瞄准射击，参考瑞典萨博公司卡尔·古斯塔夫无后坐力炮实战手册射击方法：500 m以内目标均采用统一的射击弹道进行瞄准射击，即射程为600 m的弹道，针对500 m内不同距离的目标只需根据实际距离在弹上进行引信装定即可；而对于500 m以外的目标，采用目标距离加100 m的弹道线进行射击，并在弹上根据实际目标距离进行装定。以此实现其杀伤榴弹在目标顶部一定距离处空炸，提高毁伤效率。

根据上文建立的外弹道方程组，结合以上射击方法要求分别计算300 m，500 m，800 m目标的标准射击弹道线如图2和图3所示。

根据外弹道计算结果可以得到作战条件下的瞄准参数以及弹丸时间引信的装定参数，具体结果如表1所示。

表1 射击瞄准参数及引信装定参数

2 空炸榴弹空间散布规律

2.1 模拟方法

评估空炸榴弹空间散布规律的方法与常规密集度计算方法一致，利用距离概率误差Ex，方向概率误差Ez和高低概率误差Ey进行评定，具体计算公式为：

(11)

影响空炸榴弹空间散布(密集度)的因素很多，对于火炮系统，组成系统的火炮条件、弹药条件、目标探测与计算精度、发射阵地条件及气象条件等都对密集度产生影响，其中很多因素相互关联和相互影响。基于目前的认识，概括起来主要有以下几个方面：影响高低(距离)散布的主要因素是弹道系数散布、初速散布、射角(垂直跳角)散布，时间引信误差[9-10](0.01 s，0.10 s，0.20 s，0.30 s)，弹丸质量误差和纵风散布等；影响方向散布的主要因素是偏流散布、水平跳角和横风散布等。

为了充分利用计算机对实际射击过程中随机因素进行模拟，本文采用蒙特卡罗方法[11]进行模拟打靶，其中模拟过程中考虑的影响因素如表2所示。

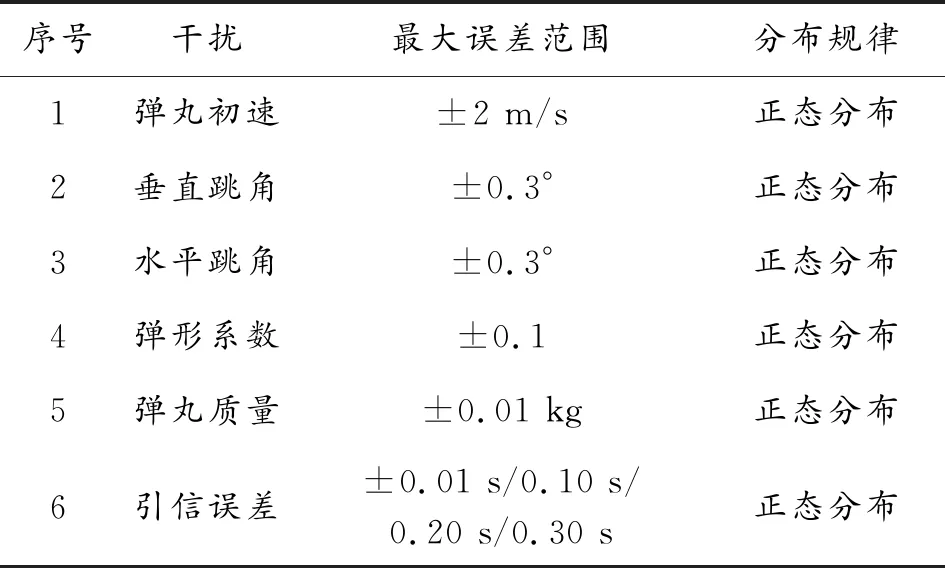
表2 干扰因素误差

表2中的误差项及最大误差范围是影响模拟打靶精度的另一个重要因素，为了控制精度，表中参数综合参考了试验数据，专家意见以及相关参考文献，因此具有较高的可信度，可以满足模拟打靶要求。

2.2 模拟结果

模拟打靶的精度随着模拟次数的增加而提高，综合考虑打靶精度和计算时间效率，每个目标距离进行1 200发模拟打靶，采用4种时间精度的引信进行装定，每种方案各进行300发射击。模拟得到以下散布结果(以300 m处结果为例)，其中图4中深色区域为空炸榴弹的空间分布情况，而图中的浅色区域为空间分布在三个平面内的投影情况。

在图4中，X表示射程，Y表示弹道高，Z表示射击方向，表3表示了空间散布概率误差的具体数据。根据以上模拟结果可知，随着时间引信精度的提高，射程方向上的概率误差Ex大幅度降低，而高低误差Ey和方向误差Ez的变化并不显著。采用高精度引信可以大幅提高时间装定的精度，进而降低弹丸射程方向的概率误差，提高射程方向密集度。

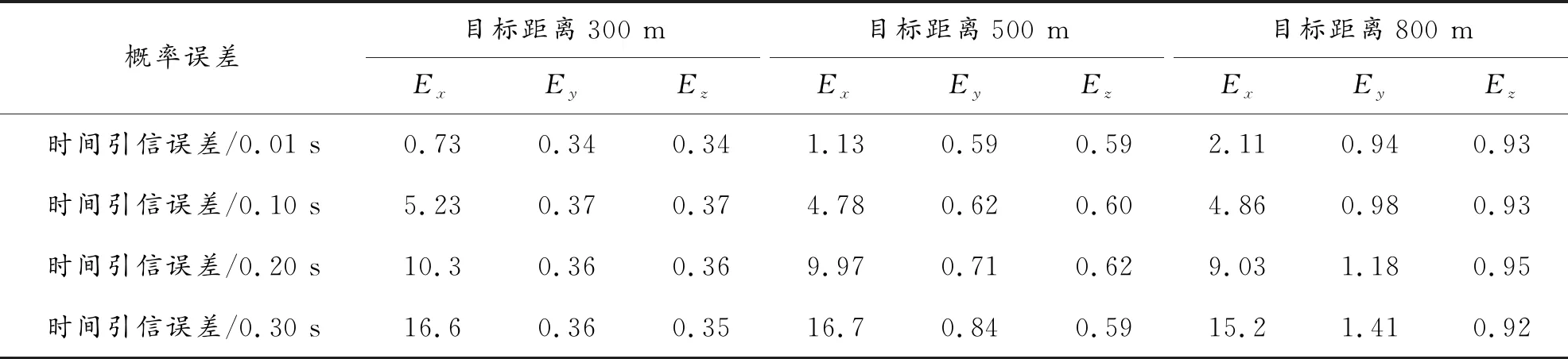
表3 空间散布概率误差

3 作战效能的概率计算

榴弹属于非接触式毁伤弹药，该类弹药毁伤目标是由于冲击波或破片的作用。确定此类弹药的毁伤作用效率主要采用坐标毁伤定律G(x,y,z)，即目标的毁伤概率与弹药相对目标的爆炸位置的函数关系[12]。对于单兵空炸榴弹而言，由于其射角小，弹道平直，所以其在目标上空爆炸时基本呈水平状态如图5所示，此时在地面产生的破片场可以近似认为是一个矩形区域，如图6所示。由此便可以将坐标毁伤定律进行简化，即破片场覆盖区域内的目标绝对毁伤G(x,y,z)=1，而覆盖区域外的目标绝对不毁伤G(x,y,z)=0，坐标毁伤定律呈阶梯形式。然而在进行作战效能评估时，只考虑毁伤概率是不够的，还需要将其与射击效率相结合。

3.1 射击效率评估

在任何类型的射击中都存在散布，这个随机变量的分布率由弹药的命中点(或爆炸位置表征)，被称为散布率。通常情况下，给定的散布率是概率密度φ(x,z)。对于空炸榴弹而言，其具有空间散布特点，因此概率密度可以表征为φ(x,y,z)，此时φ(x,y,z)dxdydz为在元体积dxdydz中具有弹药爆炸的概率。考虑一个简单的随机平面散布情况，首先选择一个固定的平面，在其上建立直角坐标系XOZ。当非接触弹药对海面或地面目标射击时，如果X轴与射击方向一致，则沿X轴的散布表征射程散布，沿Z轴的散布表征方向散布。此时，散布率将具有最简单的形式：

(12)

在实际作战的有效评估中，不常使用σx，σz，而是采用沿OX，OZ轴的概率误差，分别表示为Ex，Ez：

(13)

采用概率误差是非常方便的，Ex表示在射程方向上，有50%的命中点(或爆炸位置)位于X=±Ex的范围内，Ez表示在偏移方向上，有50%的命中点(或爆炸位置)位于Z=±Ez的范围内。此时的散布率具有以下形式：

(14)

其中，射程偏差(Ex)与方向偏差(Ez)通常被认为是独立的。因此，这些值可以被互相独立的处理。

3.2 作战效能评估

对于单兵空炸榴弹而言，其主要作战使命之一是对分布在一定区域内的敌方有生力量进行覆盖杀伤。根据上文对坐标毁伤定律的阶梯形式简化，以及单兵空炸榴弹破片场的描述可知，其实现毁伤的爆炸点位置(根据目标位置和破片场的宽度a确定)可简化为一个矩形区域如图7所示，即弹丸在该区域爆炸，目标绝对毁伤。此时，便可以得到单发射击单个目标的毁伤概率计算公式：

(14)

其中:φ(x,z)为散布率；G(x,z)为坐标毁伤定律，呈阶梯形式，即毁伤G(x,z)=1，不毁伤G(x,z)=0。

在大多数情况下，积分式(14)由已知的函数表示，当弹丸实现毁伤的爆炸点位置是如图7所示的矩形时，根据概论统计知识可以方便地给出相应的计算公式为：

(15)

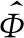
(16)

通过方程式(15)可以计算出射击一发时单个目标的毁伤概率，如果不考虑射击相关性，当进行n发射击时，该目标的毁伤概率为：

(17)

当每发射击下的目标毁伤概率相等时，方程式(17)可以简化为Wn=1-(1-W1)n。

以上讨论了单个目标毁伤概率的计算公式。对于分布在一定区域内的敌方有生力量而言，属于多目标毁伤的情况。大多数情况下，对一组多目标射击的任务构成是命中尽可能多的组成单元。在这种情况下，为了评价武器的作战效能，往往选择被毁伤目标的平均数(数学期望)作为评估指标，即：

Mm=M[Xm]

(18)

其中随机变量Xm表示毁伤目标的数目。该方程给出了数学期望最普遍的形式，适合任意多目标射击的情况。为了推导毁伤单元数学期望数的公式，我们提出毁伤目标的总数是m个随机变量的总和：

(19)

对于第j个目标单元对应的Xj，定义如下：

如果第j个单元被毁伤，Xj=1；

如果第j个单元未被毁伤，Xj=0；

从上面的方程中很容易发现，毁伤目标的总数Xm等于所有随机变量Xj的总和，由复杂数学期望的定理可得：

(20)

用Wj表示在所有射击完成时第j个目标单元的毁伤概率。于是，根据数学期望的定义有：

M[Wj]=Wj·1+(1-Wj)·0=Wj

(21)

将方程(21)代入方程(20)可以得到：

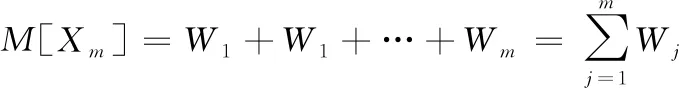
(22)

3.3 算例及结果

根据第二章模拟打靶结果，采用不同时间精度引信的差异主要体现在弹丸射程散布，而引信精度对弹丸方向散布和高低散布的影响较小，特别是针对近距离目标。尽管如此，在进行某一距离处的作战效能计算时，为了保证评估结果的准确性，仍然需要考虑弹丸的空间散布影响。然而在分析时间引信精度对某一距离处作战效能的影响计算时，炸高散布变化的影响远小于射程散布变化的影响。因此为了简化计算，可以不考虑炸高的散布。

为了探讨引信误差和破片散布扇形角对单兵空炸榴弹作战效能的影响，我们对弹丸及目标参数做如下假设：

1) 弹丸分别采用最大误差范围是±0.01 s，±0.10 s，±0.20 s，±0.30 s的4种时间引信；

2) 由于射角较小，假设弹丸空炸时均处于水平状态；

3) 弹丸破片飞散扇形角分别为30°和60°，且破片飞散中心角均为90°，其密集杀伤半径为20 m；

4) 300 m处目标上方弹丸的炸高均为8 m(参照图2)；

5) 敌方一个9人的标准战斗班组分布在300 m处一个30 m×30 m的正方形区域，如图8所示；

6) 作战中不能获悉敌班组各个成员的具体位置，射击时将目标区域看作一个组目标进行瞄准射击，瞄准点为其散布区域正中心；

7) 多发射击时，不观察结果，不转移射击，不考虑射击相关性。

根据前面介绍的方法及对弹丸目标参数的假设，对单兵空炸榴弹的作战效能进行计算评估可以得到以下结果。

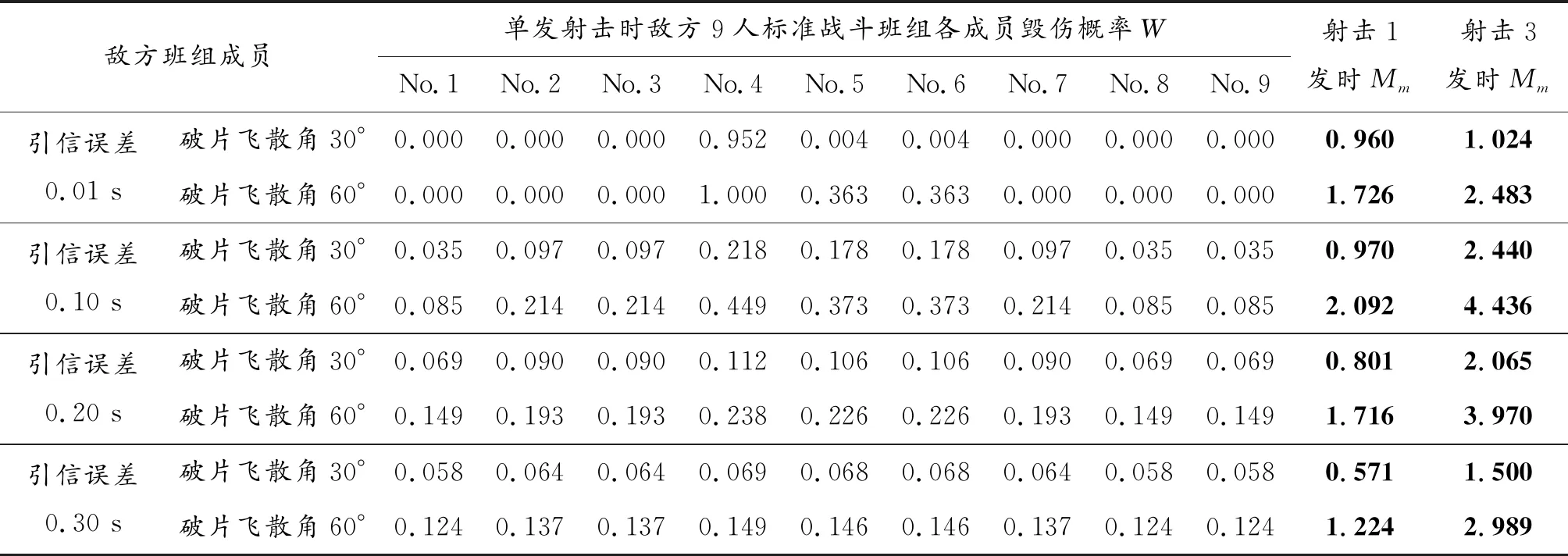
表4 敌方标准战斗班组分布为(a)时的毁伤效能

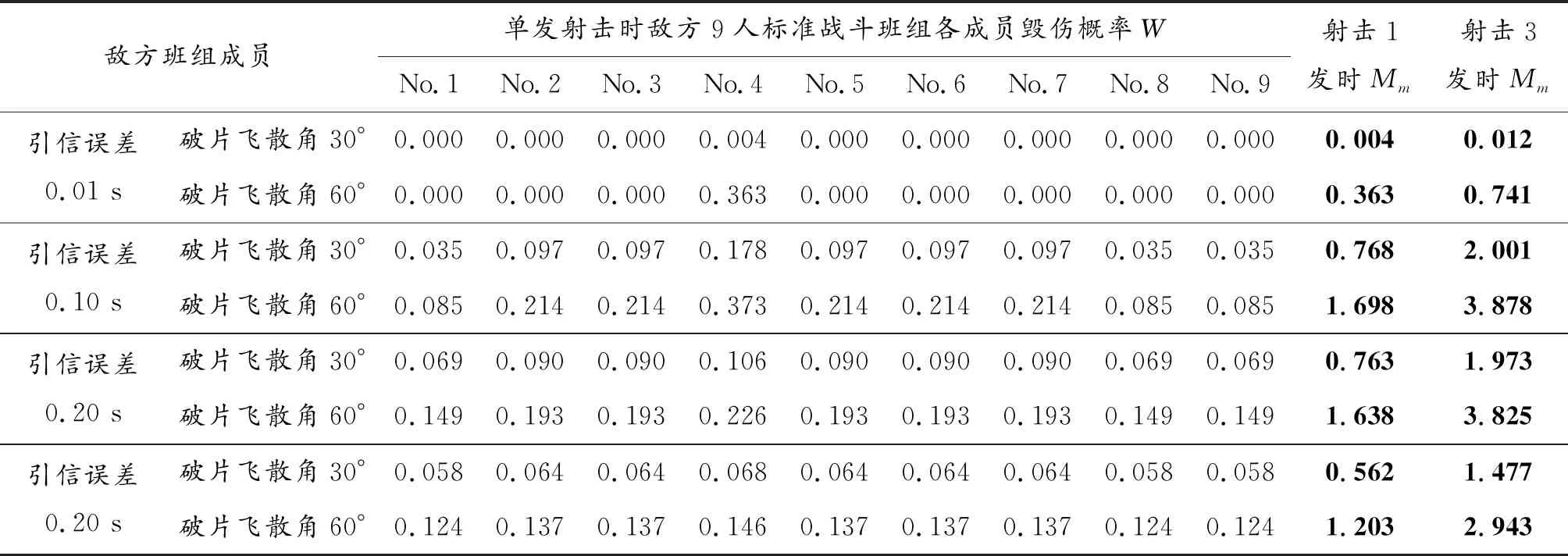
表5 敌方标准战斗班组分布为(b)时的毁伤效能

图8给出了敌方一个9人的标准战斗班组分布情况，其中相比图8(a)中的分布，图8(b)中的成员No.4，No.5，No.6沿火线方向移动5m。表4和表5分别给出了敌方标准战斗班组在两种不同的分布条件下，单兵空炸榴弹的作战毁伤效能结果。根据结果可知：在不提高破片飞散角的情况下，提高时间引信的精度时，敌班组成员被杀伤的数学期望数先增大后减小；在不提高时间引信精度的情况下，提高弹丸破片飞散角(由30°提高到60°)时，敌班组成员被杀伤的数学期望数平均提高两倍以上。此外，随着时间引信精度的提高，单兵空炸榴弹作战效能受到目标分布状态的影响逐渐增大。因此，在单兵空炸榴弹的研制过程中，需要合理选择时间引信精度。