基于强跟踪滤波的单脉冲星/惯性/星光组合导航算法
2018-08-27王宏力由四海何贻洋
王宏力,许 强,何 星,由四海,何贻洋
(火箭军工程大学 导弹工程学院, 西安 710025)
随着现代科技的发展,战争对武器的要求也越来越高。弹道导弹作为国之重器,是一个国家军事实力的重要体现。由于各种拦截及干扰手段的出现,弹道导弹要想实现有效突防和精准打击,就必须保证导航系统不仅具有较高的精度,而且也要满足自主性和抗干扰性要求。
目前,弹道导弹常用的导航方式为惯性导航。其具有信息更新速率高,隐蔽性好,不易受干扰等优点,但是会存在严重的误差累积[1]。当前,实际武器装备上常通过多种导航方式组合的方法提高精度。对于弹道导弹而言,主要增加的组合导航方式为卫星导航与星光导航[2-4]。但引入卫星导航之后,导弹本身的抗干扰性会降低,在特殊时期可能根本无法使用[5]。这对于可靠性要求较高的中远程弹道导弹而言比较致命[6]。如果不加入卫星导航,采用惯性/星光组合导航方式,其虽为一种被动、无源的自主性导航,但是无法对加速度计偏置造成的导航误差进行估计和补偿,位置和速度仍然会存在一定程度的累积[7-8]。
X射线脉冲星导航是近几年发展起来的另一种天文导航方式。可通过对比模型预测的脉冲到达时间(Time of Arrival,TOA)与计算所得的脉冲到达时间之间的差值,确定航天器的位置及速度误差。X射线脉冲星导航相对于卫星导航具有抗干扰性强,可靠性高等优点,是一种极具潜力的导航方式[9-11],许多学者也都研究了与其相关的组合导航算法[12-14],但是以弹道导弹为背景的研究较少。
单独的脉冲星导航如果要实现绝对定位必须要同时观测三颗以上的脉冲星。当前X射线脉冲星探测器的面积约在平米量级。一方面,添加3个不同的脉冲星探测器将大大增加导弹的载荷。另一方面,在其工作的中段,导弹姿态较难同时完成三颗脉冲星的对准。并且要想得到信噪比较高的脉冲信号,需要进行较长时间的光子累积,导致脉冲星导航开始工作时导弹基本已经为中段末期,此时位置和速度已经产生较大偏差,而X射线脉冲星导航所能够提供的修正次数又较为有限。所以本文结合星光导航及惯性导航,设计一种基于强跟踪滤波的单脉冲星/惯性/星光组合导航算法。该算法通过引入一颗脉冲星的脉冲TOA观测信息,改善惯性/星光组合导航中加速度计偏置估计不准确的问题。并在脉冲星导航工作时引入强跟踪滤波,增大观测量在估计结果中的比重,加强单次脉冲星导航的位置和速度误差修正效果,有效提高估计精度。
1 强跟踪滤波器
本文中使用带有次优渐消因子的强跟踪卡尔曼滤波器(Suboptimal Fading Extended Kalman Filter,SFEKF)。
考虑如下的非线性离散系统:
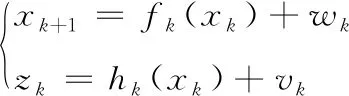
其中:xk和zk分别为n维状态向量和m维系统量测向量;wk和vk分别为n维系统噪声和m维量测噪声;fk(·)和hk(·)分别为系统非线性状态函数和量测函数。
假设1:wk和vk是互不相关的高斯白噪声,且满足如下统计特性:
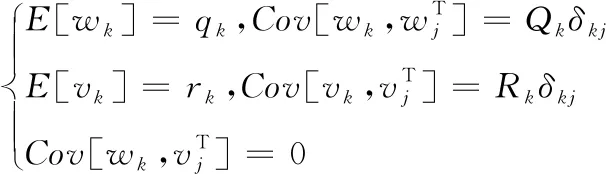
其中,Qk和Rk均为正定对称阵;δkj为Kronecker-δ函数。
假设2:初始状态x0与wk、vk互不相关,且服从高斯正态分布,其均值和协方差为:
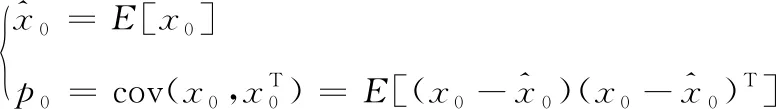
通过参考文献[15]可得,SFEKF的递推公式相对于EKF而言最大差别在于误差方差阵的一步预测公式多了一个系数因子Lmd。如下所示:
其中:
次优渐消因子Lmd可通过以下过程求得:
其中,ρ为遗忘因子,常取0.95。
2 组合导航算法设计
2.1 组合导航方案
由于X射线脉冲星导航需要的脉冲累积时间为数百乃至上千秒,故可将第1次脉冲累积周期之后的其他每一次脉冲累积周期与前一次周期重叠一部分,关系说明如图1所示。这样一来,只有第1个脉冲信号会等待完整的一个累积周期,从第2个脉冲星信号开始可缩短输出周期,增加脉冲星导航对导弹的修正次数。
即使使用这种脉冲累积方法,为保证信号质量,脉冲星导航的输出周期仍需要维持在百秒量级。所以,为降低组合导航算法的复杂性,可设置脉冲星导航的输出周期为星光导航的整数倍,星光导航的输出周期为惯性导航的整数倍。导航系统中仅存在纯惯性、惯性-星光、惯性-星光-脉冲星3种工作模式。在无脉冲星导航信号时,使用传统扩展卡尔曼滤波(Extended Kalman Filter,EKF)进行惯性及星光的组合导航解算。存在脉冲信号时,添加次优渐消因子,变为强跟踪滤波。以捷联惯性导航(Strapdown Inertial Navigation System,SINS)为例,组合导航系统的工作流程如图2所示。
2.2 状态方程
组合导航系统以发射惯性坐标系为基准,状态量可以选为X=[φx,φy,φz,δVx,δVy,δVz,δx,δy,δz,εx,εy,εz, ▽x, ▽y, ▽z],依次代表3个方向的平台失准角、发射惯性坐标系的3个速度和位置误差、3个陀螺仪常值漂移、3个加速度计常值偏置。
则状态方程可表述为[16]
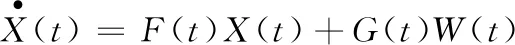
2.3 观测方程
当仅存在星光信号,无脉冲星信号时,使用EKF进行两者的信息融合,其观测方程为
其中:V(t)为星敏感器的量测噪声,与星敏感器的自身参数有关。
X射线脉冲星导航的基本观测模型如下所示[17]
(1)
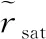

通过文献[18]中的分析可知,式(1)右侧除第一项外其余项的量级都非常的小,在使用位置误差作为状态量而不进行绝对定位时可以省略。则本文中脉冲星导航部分的观测模型可以简化为
式中:ΔxBCRS为导弹在BCRS坐标系中的位置误差。
由于脉冲星导航的观测模型使用的是导弹在BCRS中的位置误差,故需要将其转化到发射惯性坐标系中。
导弹在发射惯性坐标系中的位置误差Δx与BCRS坐标系中的位置误差ΔxBCRS满足:
结合以上分析,该模式下的观测方程可以写为
3 仿真分析
3.1 仿真参数设置
地球赤道半径Re=6 378.245 km,地球扁率e=1/298,地球自转角速率we=7.272 205×10-5弧度/s,地球重力加速度g0=9.780 326 771 4 m/s2,地球引力常数GM=3.986 005×1014m3/s2,重力二阶带谐系数J2=0.001 082 63。
发射点纬度λ=39.98°N,发射点经度μ=116.34°E,发射方位角A=90°,仿真时间1 500 s,主动段转弯结束时间为60 s,发动机关机时间为180 s,推力加速度为45 m/s2,陀螺常值漂移0.1 °/h,加速度常值偏置50 μg,陀螺噪声标准差0.05 °/h,加速度计噪声标准差25 μg。仿真使用的标准弹道如图3所示。
SINS采样周期0.01 s,CNS采样周期0.1 s,XPNAV采样周期100 s,X射线探测器脉冲累积时间 1 000 s,面积1 m2。分别使用B0531+21、B1821-24及B1937+21三颗脉冲星进行仿真实验,其具体参数见表1所示,并通过文献[20]中的噪声计算公式计算出三颗脉冲星的观测噪声标准差分别为77.78 m,232.23 m,247.02 m。星敏感器精度3″。初始失准角[90″,90″,90″],初始比例因子1.5。
其中,D0为脉冲星距离太阳系质心的距离,P为脉冲周期,W为脉冲宽度,Fx为X射线脉冲星辐射光子流量,pf为在一个脉冲周期内的脉冲辐射流量与平均辐射流量之比,Bx为宇宙X射线背景流量。
3.2 仿真结果
限于篇幅,在图4中仅展示使用B1821-24脉冲星的组合导航仿真过程,使用其余脉冲星的仿真结果最终统计于表2。
通过分析以上仿真结果可得,在第180.1 s,星敏感器开始工作,此时系统相当于惯性/星光组合导航系统,可以有效消除由陀螺漂移及初始失准角造成的位置、速度误差累积,大幅提高精度。但是由于无法弥补加速度计偏置造成的导航误差,所以系统仍然存在一定的漂移。在第1 180 s,X射线探测器开始输出TOA信号,并此后以100 s为周期持续输出。当存在TOA信号时,基于EKF的单脉冲/惯性/星光组合导航虽然有所改进,但由于卡尔曼滤波的“中和”作用,效果不是很明显,最好的情况下位置和速度仅比惯性/星光组合导航分别提高28.8%和26.7%。而引入SFEKF后,增加脉冲星观测量在最终结果中的比重,校正效果提升明显,最好的情况下位置和速度可以比惯性/星光组合导航分别提高63.8%和75.9%。
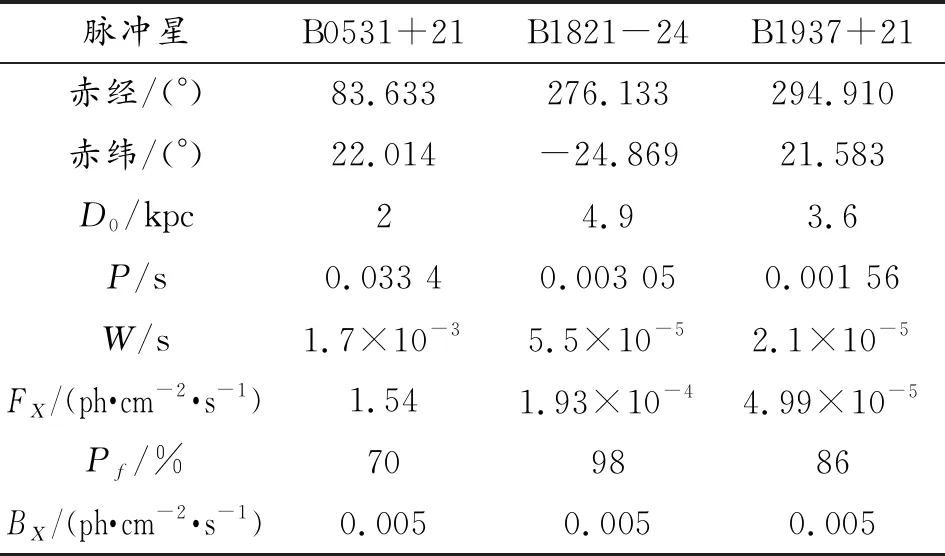
表1 导航用脉冲星参数
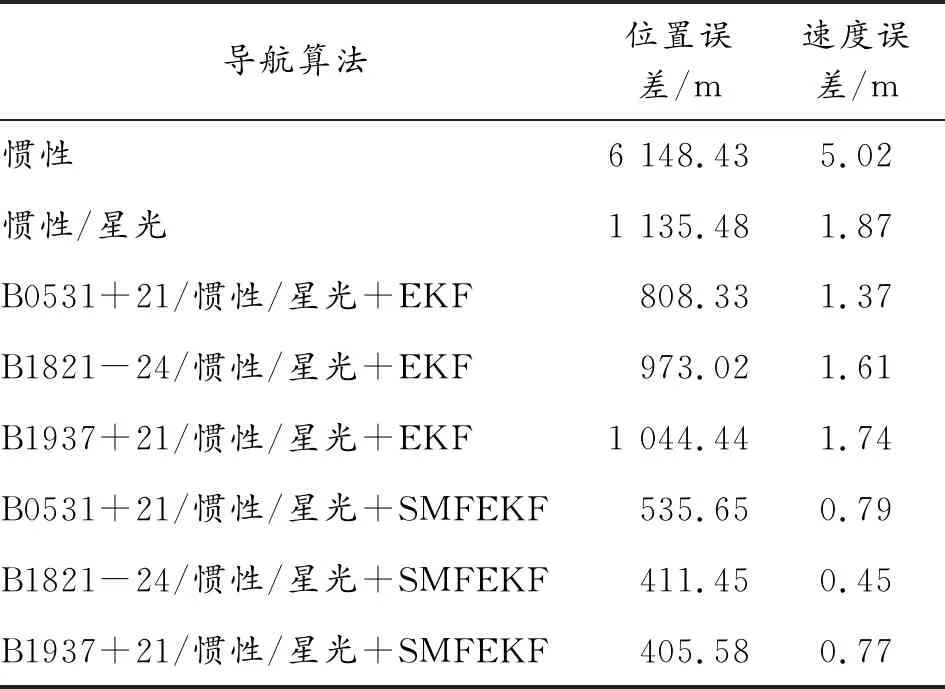
表2 不同导航算法结果统计
4 结论
本文研究了基于强跟踪滤波的单脉冲星/惯性/星光组合导航算法,通过在惯性/星光组合导航中加入脉冲星的观测信息,削弱加速度计偏置导致的位置和速度误差累积。同时引入强跟踪滤波,使在脉冲星导航工作时的中段末期,位置、速度误差减小,提高传统扩展卡尔曼滤波计算精度。通过仿真分析,证明了本文提出的算法的有效性。
