基于Copula函数及确定优化的结构可靠度评估

2018-08-27赵维涛李久安祁武超

兵器装备工程学报 2018年12期

赵维涛，李久安，祁武超

(沈阳航空航天大学航空宇航学院，沈阳 110136)

在工程设计中，随着对结构可靠性要求的不断提高，人们将结构设计变量间的相关性和不确定性逐步纳入到考虑范畴[1-2]。而且近年来的研究结果表明，证据变量间的相关性可能对可靠性计算结果产生较大影响，常用的独立性假设会对可靠性计算结果产生较大的误差。因此，由Sklar定理[3]发展而来的Copula函数逐步被用于处理相关性问题中，以减小由独立性假设带来的误差。近年来围绕Copula函数的研究，着重点为最优Copula函数的选择方法[4]和已知Copula函数形式条件下的参数估计方法[5-6]。目前最优Copula函数的选择常用解析法和AIC(Akaike’s information criterion)准则法，解析法需要以二元经验分布函数作为二维Copula函数的估计量，AIC准则法需要计算Copula函数的密度函数，这两种方法在使用过程中都会受到不同程度的限制。李霞[7]对Archimedean Copula函数模型选择方法的改进，充分考虑了函数的对称性及有效估计量，可更好地刻画了参数之间的相依性。任仙玲[8]等在基于核密度估计的条件下，提出了选择最优Copula函数的核密度选择原理，该方法避免了求解各Copula函数的密度函数。David Huard[9]等引入了一种基于Bayesian思想的最优Copula函数的选择方法，这种方法具有良好的理论基础，并且独立于参数的选择，可以由较少的数据得出理想的选择结果，在使用过程中具有一定的优势，本文在最优Copula函数选择环节沿用Bayesian思想。

确定性优化算法[10-11]广泛应用于工程结构设计中，优化结果可靠，收敛效率高，MATLAB编写程序简明。而暴力组合(枚举法)在求解极限状态函数的极值时，可能会由于节点间距选择不当，造成计算精度差或计算效率低等问题。鉴于确定性优化算法中的迭代求解方式可以避免以上问题出现，本文将该算法嵌入到基于Copula函数的结构可靠度评估过程中，代替原有的极值求解方法，可以避免由于节点间距选择不当而产生的误差，并且提高计算效率。本文通过算例证明所提方法在使用过程中具有一定优势。

1 Sklar定理及Copula函数

Sklar定理[3]是在1959年由Sklar首次提出，初步展示了一维边缘分布和联合分布函数的关系以及相关的变化特征，阐明Copula函数在多维分布及其一维边缘分布的关系中所扮演的重要角色。Copula函数在统计学中的重要性主要体现在Sklar定理。以二维分布为例，设H是一个联合分布函数，其边缘分布函数分别是FX(x)和RY(y)，则一定有一个Copula函数C，使得对实数域中所有的x和y有式(1)成立，若FX(x)和RY(y)是连续的，则C是唯一存在的，否则C在实数域中不是唯一确定的。

H(x,y)=C(FX(x),RY(y))

(1)

将Sklar定理推广到n维，边缘分布为F1(x1),F2(x2),…,Fn(xn)的n维联合分布函数可以表示为：

F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))

(2)

式(2)中，C为与F对应的Copula函数。

如果边缘分布函数均为连续函数，则存在唯一的Copula函数C使得下式成立：

(3)

式(3)中，u1=F1(x1),u2=F2(x2),…,un=Fn(xn)，且满足ui∈[0,1],i=1,2,…,n。

对式(2)两侧求导，可得X的联合概率密度函数为：

(4)

式(4)中，c为Copula函数C的概率密度函数。其求解关系式如下：

(5)

Copula函数C(u1,u2,…,un)的上下界可由Fréchet-Hoeffding边界[12]给出，具体为：

W(u1,u2,…,un)≤C(u1,u2,…,un)≤M(u1,u2,…,un)

(6)

式(6)中：M(u1,u2,…,un)=min(u1,u2,…,un)，W(u1,u2,…,un)=max(u1+u2+…+un-n+1,0)。

2 改进的结构可靠性分析方法

2.1 证据理论与可靠度区间

D-S证据理论即Dempster-Shafer理论[13]，可以对各类不确定信息进行合理地描述和处理，旨在减小由多重不确定因素耦合作用造成的影响，是处理不确定信息的有力工具。将证据理论与可靠度评估结合，能够很好地解决涉及多源不确定因素的可靠度评估问题，对可靠度区间上下限进行准确量化，而且具有较高的求解效率。

关于证据理论，最重要的基础理论之一为基本可信度分配函数(Basic Probability Assignment，BPA)。令2Θ表示识别框架Θ的幂集，由Θ包含的所有命题可能组成。证据理论用基本可信度分配表示对命题A的信任程度，BPA是一个满足如下公理的映射：

0≤m(A)≤1, ∀A∈2Θ

m(φ)=0

∑A∈Θm(A)=1

(7)

式(7)中：φ表示空集，对m(A)>0的子集A称为焦元，命题A的基本可信度分配值m(A)表示证据对命题A的支持程度。

根据证据理论，可在缺乏信息的情况下，利用区间[Bel(A),Pl(A)]来描述证据对命题的支持程度，其中可信度与似真度可以由下式得出

(8)

式(8)中：B为同一识别框架下的已知证据；Bel(A)称为可信度，是完全支持A的证据BPA之和；Pl(A)为似真度，是所有完全或部分支持A的证据BPA之和。

2.2 基于Copula函数与证据理论的可靠度求解

2.2.1Kendall相关系数τ与Copula函数相关系数

Kendall秩相关系数[7]是在Copula函数研究中最常用到的相关性测度，主要是通过分析变量之间的变化是否协调来判断两变量之间的相依关系。具体以二维随机变量为例，令(x1,y1)，(x2,y2)为随机变量(X,Y)的两组观测值，若(x1-x2)(y1-y2)>0，则称(x1,y1)与(x2,y2)是一致的，即正相关的。若(x1-x2)(y1-y2)<0，则称(x1,y1)与(x2,y2)是不一致的，即负相关的。基于以上正负相关的讨论，Kendall秩相关系数可由下式得出：

(9)

式(9)中：τ是由观测值计算得出的秩相关系数；sign(·)为符号函数。

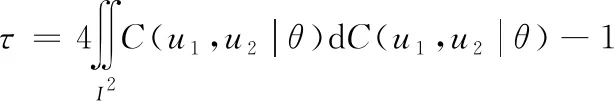
(10)

2.2.2Bayesian方法求最优Copula函数

(11)

式(11)中：Cl为第l个备选Copula函数；P(Cl)是在得出观测数据之前，Copula函数为Cl的先验概率；P(Q|Cl)为在备选Copula函数Cl条件下，数据Q的似然。

在备选Copula函数给定的情况下，P(Q)为常数，所以式(11)等价于：

P(Cl|Q)∝P(Q|Cl)P(Cl)

(12)

在实际工程设计工作中，由于对结构参数的未知性，缺乏具有说服力的先验认识，可以将P(Cl)取为相同的概率，因此最优Copula函数完全由P(Q|Cl)确定。当参数θl为离散值时，根据似然函数的定义，P(Q|Cl,θl)具体表达式为：

(13)

综上关于Bayesian思想的叙述，最优Copula函数的选择标准为：

(14)

式(14)中，arg max(·)表示求解具有最大函数值的参量。

2.3 可靠度评估方法的改进

2.3.1嵌入确定优化的可靠度评估

基于上述理论基础，本文创新性地将确定性优化算法嵌入到可靠度评估过程中，将原有的可靠度评估方法进行改进。首先考虑，一个含有n维证据矢量X的不确定性结构，其可靠域G可定义为[15]

G{g∶g(x1,x2,…,xn)≥0}

(15)

式(15)中，g为功能函数，定义一个n维识别框架如下：

D=X1×X2×…×Xn=

{dk=[x1i,x2j,…,xnl];

x1i∈X1,x2j∈X2,…,xnl∈Xn}

(16)

式(16)中：[x1i,x2j,…,xnl]构成第k个焦元dk，i,j,…,l为证据变量所分区间数量，且满足k=i×j×…×l。

证据变量联合BPA和可靠域G，结构安全的可信度Bel和似真度Pl可以通过式(8)得出。

(17)

理论上，真实的结构可靠度P=P{g(x1,…,xn)≥0}应该属于区间[Bel(G),Pl(G)]。为计算上述两个可靠性测度Bel和Pl则需要判断dk⊆G(焦元dk完全位于可靠域内)或dk∩G≠φ(焦元d完全位于或者部分位于可靠域内)，为此需要计算极限状态方程在每个焦元dk上的极值。本文将利用确定性优化算法求解极值，该方法具有可行性，并且相比较简单极值求解，具有一定优势确定性优化模型如下：

(18)

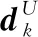
(19)

对于焦元dk，如果gmin和gmax均为正，则dk⊆G，焦元dk的BPA同时计入Bel(G)和Pl(G)中；如果gmin和gmax均为负，则dk∩G=φ焦元dk的BPA既不计入Bel(G)，也不计入Pl(G)中；如果gmin为负，gmax为正，则dk∩G≠φ，焦元dk的BPA计入Pl(G)但不计入Bel(G)。

2.3.2本文流程

基于以上所提的理论基础，总结得出本文方法的总体流程如下：

1) 设计变量X样本值，边缘BPA。

2) 将样本值转换为[0,1]上的均匀变量，并计算Kendall秩相关系数。

3) 运用Bayesian方法求出最优Copula函数。

4) 利用优化算法式(18)求解出每个焦元上极限状态函数极值[gmin,gmax]。

5) 获得结构可靠度区间[Bel(G),Pl(G)]。

本文所提出的改进方法流程图如图1所示。

3 算例

本文所提出的改进可靠度评估改进方法涉及到确定性优化算法，因此在极限状态函数极值计算时调用MATLAB优化工具箱中的fmincon[16-17]函数求解。

3.1 算例1

矩形截面梁[18]载荷位置与截面尺寸如图2所示，本算例根据对该梁固定端最大应力处进行强度校核，得出极限状态方程如下：

g(x1,x2)=S-3 000x1-1 500x2

(20)

式(20)中：x1和x2为证据变量，也是确定性优化算法中的优化变量；S为悬臂梁极限强度。

在本算例中，证据变量离散点数据来源于文献[18]，并对材料参数进行调整后，将自编程序计算结果作为对比参考。将证据变量x1,x2转换为在[0,1]上的均匀变量。然后由式(9)计算得出Kendall秩相关系数τ=0.683 3。根据式(10)中给出的Copula函数相关性系数θ与Kendall秩相关系数τ的微积分关系，求得各Copula函数的相关性系数θ见表1。对于该算例，沿用Bayesian方法选取最优Copula函数，各Copula函数的权重比由表1给出，符合证据变量的最优Copula函数为Gumbel Copula函数。证据变量x1,x2的区间分布与边缘BPA由表2给出。当充分考虑证据理论相关性模型与最优Copula函数的内在关系后，本文将确定性优化算法的表达式(18)引入可靠性评估过程中，得出极限状态函数在各焦元中的极值。在此基础上，悬臂梁可靠度评估结果如表3所示，从结果中可以明显看出，本文算法在保证计算精度的条件下，很大程度地提高了计算效率。

表1 最优Copula函数选择

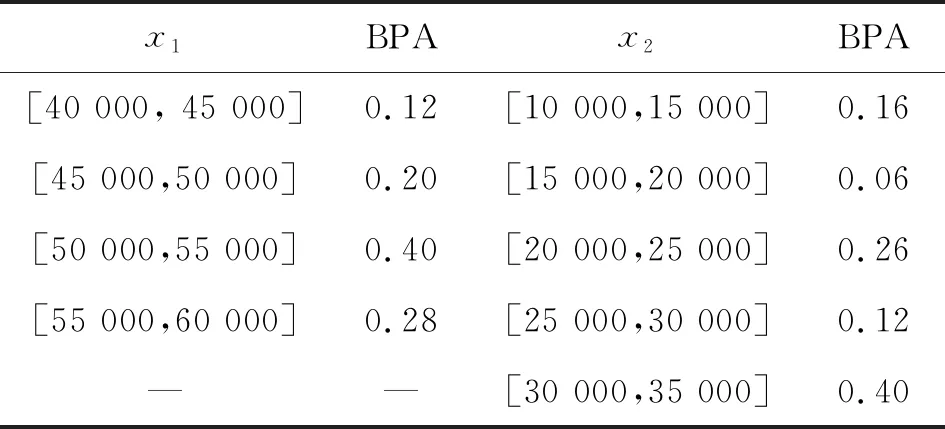
表2 边缘BPA

表3 可靠度评估结果

3.2 算例2

某齿轮减速箱的齿轮组及箱体如图3所示，本算例中例包含三个证据变量，分析后得出的极限状态函数如下：

(21)

式(21)中：φ1为输出轴直径；φ2为输入轴直径；x1为输出轴固定轴承的间距。

本算例因为无法进行试验操作得出数据，所以通过MATLAB随机生成符合Gaussian Copula函数分布特征的离散数据点，作为可靠度评估的数据来源。通过后续的计算分析，也间接验证了本文最优Copula函数选择方法的有效性与正确性。

在本算例中，将进一步计算包含三维证据变量x1，φ1和φ2的齿轮减速机构的可靠度区间。首先根据证据变量离散数据点的一致性概率求出Kendall秩相关系数为τ=0.508 0，然后由Copula相关性系数θ与Kendall秩相关系数τ的微积分关系，求得各Copula函数的相关性系数见表4，同时表4也给出了由Bayesian方法求出的各Copula函数的权重比，本算例最优Copula函数为Gaussian Copula函数。证据变量x1，φ1和φ2的区间分布及边缘BPA，由表5给出。在此基础上，齿轮减速机构可靠度评估过程及结果如表6所示。

由表6所示的计算过程和结果对比可以看出，当节点间距较大时，暴力组合(枚举法)可以提高计算效率，但是会引起可靠度评估结果不稳定。随着节点间距逐渐减小，可靠度评估结果逐渐趋于稳定，但是计算量较大，计算耗时长。当引进确定性优化迭代计算过程代替极值求解方法，可以通过少量迭代计算得出较为理想的评估结果，该方法在保证计算精度的条件下，很大程度地提高了计算效率。

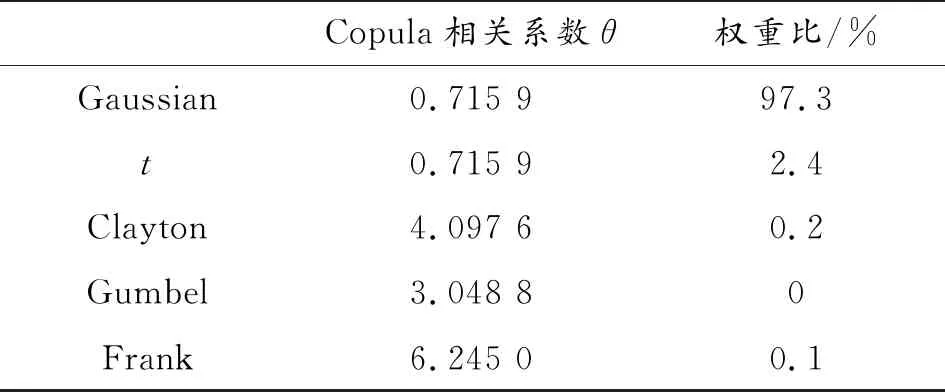
表4 最优Copula函数选择

表5 边缘BPA

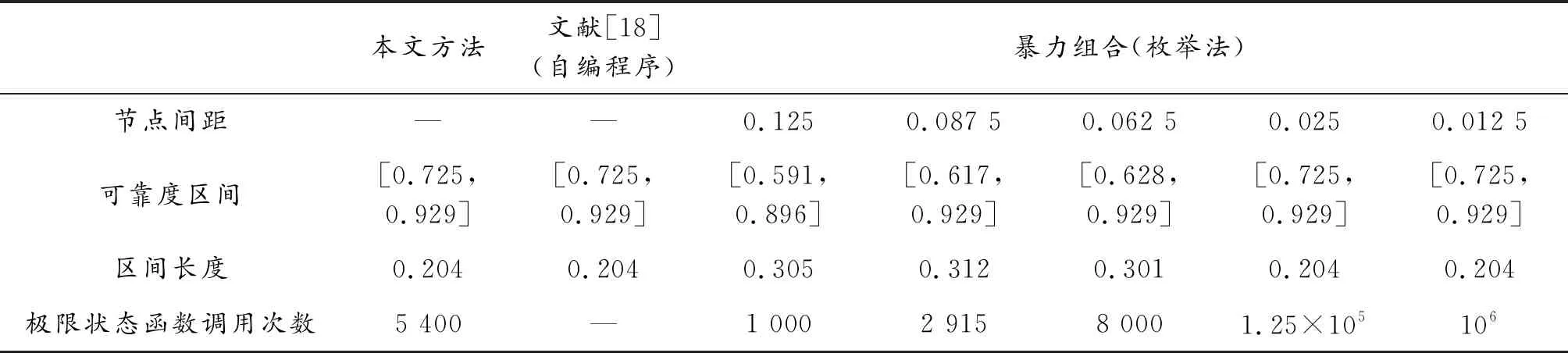
表6 可靠度评估结果

3.3 算例3

十杆桁架结构[19-20]如图4所示，图4中水平方向和竖直方向桁架长度L=9.144 m，材料弹性模量E=68 948 MPa。其中1～6杆横截面积为70 cm2，7～10杆横截面积为65 cm2，节点4受到竖直作用力x1，节点2受到竖直作用力x2和水平作用力x3。本算例将节点2处的竖向位移d2max作为最大位移极限，隐式极限状态方程如下：

g(x1,x2,x3)=d2max-δ2(x1,x2,x3)

(22)

式(22)中：δ2(x1,x2,x3)为节点2处的竖向位移。

在本算例中，x1,x2,x3离散数据生成原理同算例2，此处不再赘述。对十杆桁架结构进行可靠度评估，着重研究本文算法与其他算法在计算精度及计算效率方面的比较。首先，由证据变量x1,x2,x3的离散数据点的一致性概率得出秩相关系数τ=0.505 1，各备选Copula函数的相关性系数θ见表7，同时表7也给出了各备选Copula函数的权重比，本算例的最优Copula函数为t Copula。证据变量x1,x2,x3的区间分布及边缘BPA由表8给出。

本文方法与其他方法的计算结果见表9，从表9中可以看出，本文方法与文献[18]方法求得的可靠度区间一致，说明本文方法具有一定的计算精度。文献[20]中的响应面法选取106个样本点进行分析，得出可靠概率Pr=0.879 1，文献[21]静态响应矩法计算得出的可靠概率Pr=0.888 2。可以看出，所涉及文献中计算得出的可靠度都介于本文方法计算得出的可靠度区间内。通过该算例可知，本文方法在求解可靠度区间问题是可行的。