基于主从记忆空间模型的时空上下文跟踪算法
2018-08-31赵宇飞郭拯坤王枫宁
宋 勇,李 旭,赵宇飞,郭拯坤,杨 昕,王枫宁
(1.北京理工大学光电学院, 北京 100081;2.精密光电测试仪器及技术北京市重点实验室, 北京 100081)
作为计算机视觉领域的重要研究方向,目标跟踪算法在视频监控、人机交互、智能交通等领域具有广泛的应用前景[1]。根据不同的建模方式,目标跟踪算法可分为三类:基于目标特征匹配式跟踪算法[2],基于目标和背景特征判别式跟踪算法[3]和基于目标和背景相关性跟踪算法[4]。其中,基于目标和背景相关性跟踪算法有效利用了目标和背景信息,具有相对较高的跟踪精度。
作为一种新型基于目标和背景相关性的跟踪算法,时空上下文目标跟踪算法[4](Spatio-Temporal Context Learning,STC)通过贝叶斯框架对目标及其周围区域的时空关系进行建模,得到目标及其周围区域的统计相关性。根据这一时空关系计算置信图,利用置信图中似然概率最大的位置来预测新的目标位置。STC算法结合了时间信息和空间信息,考虑了目标和周围环境信息,根据傅里叶变换学习时空关系,具有较高的目标跟踪精度和速率,是一种具有重要应用前景的目标跟踪算法[5]。另一方面,由于STC算法采用固定的学习参数更新时空上下文模板,易将错误信息更新到目标模板中。当出现目标被遮挡、姿态突变、目标短暂消失后重现、环境光照变化等情况时,易出现跟偏或跟丢目标,导致目标跟踪精度下降。
针对上述问题,Wei X G等[6]将时空上下文算法与卡尔曼滤波相结合进行目标跟踪,虽在一定程度上解决了遮挡后目标漂移问题,但却难以避免模板的错误更新;XU Jian-Qiang 等[7]赋予上下文不同区域不同的权值,引入Harris角点跟踪目标,并且引入权值矩阵计算不同区域的权值,在一定程度上提高了跟踪结果的鲁棒性,但降低了算法速度;刘威等[8]采用点跟踪器完成目标初步定位,由多维特征时空上下文模型完成精确定位,提高了目标遮挡、光照变化条件下的跟踪能力,但当目标姿态变化较大时,算法跟踪性能下降。
人脑视觉系统作为人类大脑获取外界信息最主要的手段完成了人类70%以上的信息获取。人脑视觉系统具有多种信息处理机制,包括:侧抑制、记忆机制等[9]。其中,人脑记忆机制具有敏捷性、持久性、备用性的特性,有助于解决目标跟踪中的目标遮挡、姿态突变等问题[10-11]。
基于上述分析,本论文提出了一种基于主、从记忆空间模型的时空上下文跟踪算法。该算法将人脑记忆机制融入STC算法的时空上下文模板更新过程,通过构建主、从记忆空间,形成基于记忆的更新策略。通过记忆先前出现的场景,解决目标跟踪过程中的目标被遮挡、姿态突变、目标短暂消失后重现、环境光照变化等问题。同时,通过设置多个置信图峰值点作为目标位置候选点,选取与目标模板相似度最大的目标位置作为最终跟踪结果,减少置信图引起的误差,提高目标跟踪精度。实验结果表明,所提出的算法可以解决跟踪过程中的目标被遮挡、姿态突变、短暂消失后重现等条件下的跟踪精度下降问题,有利于实现鲁棒性、高精度的运动目标跟踪。
1 基于主、从记忆空间模型的STC算法
1.1 STC算法原理
STC算法通过贝叶斯框架对目标和周围区域的时空关系进行建模,得到目标及其周围区域的统计相关性。根据生物视觉系统上的视觉注意特性,得到预测目标位置的置信图。STC算法的主要过程包括:
1) 在已知第一帧跟踪窗的情况下容易得到目标置信图和先验概率;
2) 根据过程1)得到的结果,求出目标和局部上下文的空间关系h,再利用这一关系学习下一帧的时空关系H为:
Ht+1=(1-ρ)Ht+ρht
(1)
式(1)中,Ht+1为第t+1帧时空上下文模板;Ht为第t帧时空上下文模板;ht为第t帧空间上下文模板;ρ为学习参数。
3) 根据学习到的时空关系计算置信图,由置信图中似然概率最大的位置预测出新的目标位置。其中,置信图计算公式为:
c(x)=p(x|o)=∑c(z)∈xcp(x,c(z)|o)=
∑c(z)∈xcp(x|c(z),o)p(c(z)|o)
(2)
式(2)中,x表示目标位置;o表示目标出现;xc为上下文空间信息;p(c(z)|o)是上下文先验概率,定义了目标周围局部上下文的表观,如公式(3)所示;p(x|c(z),o)是条件概率,定义为建模目标与局部上下文的空间关系,如公式(4)所示。
p(c(z)|o)=I(z)ω(z-x*)
(3)
p(x|c(z),o)=h(x-z)
(4)
式(3)、(4)中,I(z)为是点z的灰度;x*为给定的目标位置;w是一个加权函数,z离x越近,权值越大;h(x-z)是一个关于目标x和局部上下文位置z的相对距离和方向的函数。
1.2 基于主、从记忆空间模型的时空上下文模板更新
本论文所提出的算法采用基于主、从记忆空间模型的时空上下文模板更新策略,更新目标和局部上下文之间的时空关系。如图1所示,该模型包括主、从两个记忆空间。其中,主记忆空间用于存储判别匹配程度的彩色直方图模板,从记忆空间用来存储时空上下文关系模板。因为时空上下文模板是一种复杂矩阵,所以借助于更直观的直方图模板作为匹配模板决定是否更新。每一层记忆空间均构建瞬时记忆、短时记忆和长时记忆三个空间,其中,短时记忆空间和长时记忆空间分别可以存储R个模板。
依据主记忆空间中的模板和目标模板的匹配程度,决定从记忆空间中的时空上下文模板是否进行更新。其中,在主记忆空间中,将当前帧跟踪结果所得到的估计模板(目标跟踪窗彩色直方图特征)存入瞬时记忆空间,依次与短时记忆空间、长时记忆空间中的目标模板进行匹配:若匹配成功,则根据更新规则对主记忆空间中目标模板进行更新,同时更新从记忆空间中的时空上下文模板;若均匹配失败,则将瞬时记忆空间中的估计模板记忆到短时记忆空间。时空上下文模板更新总体流程如图2所示。
时空上下文模板更新具体步骤为:
步骤1初始化记忆空间。
将当前帧的估计模板(彩色直方图特征)存储于瞬时记忆空间。将第一帧目标的彩色直方图特征作为当前目标模板,存储于主记忆空间中短时记忆空间的第一个位置。类似地,将第一帧时空上下文模板存储于从记忆空间中短时记忆空间的第一个位置。
步骤2与短时记忆空间匹配。
将瞬时记忆空间存储的彩色直方图与主记忆空间中短时记忆空间的R个模板依次进行匹配,采用巴氏距离计算出相似度。根据相似度与匹配阈值的比较结果确定是否匹配成功。若在短时记忆空间中匹配成功,则根据当前模板对目标模板进行更新,如式(5)所示:
qt=(1-ε)qt-1+εp
(5)
式(5)中,qt为当前模板;p是瞬时空间的估计模板;ε是学习参数。同时,从记忆空间中相对应地对时空上下文模板进行更新,如式(1)所示。
如果短时记忆空间中的R个模板匹配均不成功,则将短时记忆空间中最后一个分布记为MR,继续与长时记忆空间中的模板进行匹配。
步骤3与长时记忆空间匹配。
将瞬时记忆空间存储的彩色直方图与主长时记忆空间中的R个模板依次进行匹配,同样采用巴氏距离计算相似度。根据相似度与匹配阈值的大小比较确定是否匹配成功。
如果存在匹配模板,根据公式(1)、 (5)更新匹配模板,记短时记忆空间最后一个模板为MR。同时在不可记忆情况下提取匹配的模板遗忘MR。在MR可记忆情况下,交换匹配模板和MR。
如果长时记忆空间中也不存在匹配模板,则更换主记忆空间中的当前模板,同时从记忆空间中的时空上下文模板也相对应更换。
1.3 置信图多峰值点
在常规STC算法中,取置信图最大峰值点作为目标位置。由于置信图生成过程存在一定的误差,真实的目标位置可能在其他峰值点,而非置信图的最大峰值点处。例如:图3是FaceOcc1序列第228帧,由于置信图生成过程导致的误差,利用置信图最大峰值点求得的目标位置(实线)偏离了跟踪目标(人脸)。而真实目标位置(虚线)对应于置信图的第二峰值点。
针对上述问题,在根据时空上下文计算置信图时,基于主从记忆空间模型的STC算法设置N个目标位置候选点,从中选取与目标模板相似度最大的目标位置作为最终跟踪结果,从而减少了置信图误差对跟踪精度的影响。具体方法为:
计算求得N个候选目标跟踪窗的彩色直方图特征,记第i个彩色直方图特征为pi(i=1,2,3,…,N),记忆空间存储的目标模板为q,计算pi与q的相似度(pi与q均为L维向量)。最大相似度S的计算公式为:
(7)
取最大相似度对应的候选目标作为最终目标。
2 算法设计
基于主从记忆空间模型的STC算法,利用目标和局部上下文的统计相关性,以及由视觉注意特性学习到的先验概率,计算出下一帧中的置信图,选取最相似置信图峰值点作为目标位置。图4为基于主、从记忆空间模型的STC算法的流程框图。
具体算法步骤如下:
基于主从记忆空间模型的STC算法的具体步骤如下:
步骤1利用初始化第一帧的置信图和上下文先验概率学习第一帧的空间上下文模板,同时作为第二帧时空上下文模板。由公式(2)-(4)推导出置信图计算公式为:
c(x)=h(x)⊗(I(x)ω(x-x*))
(8)
式(8)中,I(x)为像素点x的灰度;x*为给定的目标位置;w是一个加权函数,x离x*越近,权值越大。
由式(8)结合傅里叶变换和反傅里叶变换,推导出第一帧的空间上下文模板作为第一帧的时空上下文模板,计算公式为:
(9)
步骤2学习空间上下文模板,根据t-1帧得到的目标中心位置与记忆空间匹配,根据1.2.3节的更新规则,更新得到第t帧的时空上下文模板。
步骤3学习当前帧上下文先验概率,结合步骤2得到的第t帧时空上下文模板,计算第t帧置信图,有:
(10)
根据置信图最大N个峰值点,计算目标N个目标位置候选点。
步骤4根据候选目标区域彩色直方图特征与目标模板做匹配,取相似度最大的候选点为第t帧目标位置。
步骤5匹配第t帧确定的目标窗口的彩色直方图和记忆空间中的模板,根据主记忆空间中的更新情况更新从记忆空间中时空上下文模板,用于确定t+1帧目标。
3 实验与结果分析
3.1 实验条件
以粒子滤波算法[12](PF)、压缩感知跟踪算法[13](CT)、常规时空上下文目标跟踪算法(STC)等目标跟踪算法为比较算法,开展对比实验,验证基于主从记忆空间模型的STC算法的性能。其中,PF为典型的目标跟踪算法,CT与常规STC为近年来出现的新型目标跟踪算法,其对目标外观变化和背景变化具有鲁棒性[14]。
实验采用Visual Tracker Benchmark视频测试集中的Girl序列、Crossing序列、FaceOcc1序列、Walking序列以及本论文在在背景相对复杂的实际环境中采集的Li1序列、Li2序列为实验对象。Visual Tracker Benchmark视频测试集[1]是2013年由Wu Yi等人发表在CVPR上的用来作为目标跟踪的数据集,由50个可见光序列组成,2015年,扩充到100个序列。其中,在Girl序列中,目标发生姿态变化且存在目标遮挡,图像分辨率为128(96;FaceOcc1序列中,目标发生姿态变化、反复遮挡和遮挡后重现,图像分辨率为352(288;在Crossing系列中,目标发生光照变化,图像分辨率为360(240;Walking序列帧数较多,图像分辨率为768(576。本论文采集的Li1序列、Li2序列分辨率为960×544。实验各序列的特点如表1所示。
其他实验条件设置包括:Intel(R) Core(TM) i3 CPU 3.07GHz,4.00G的PC机,MATLAB 2013a平台。实验中参数设计包括:目标位置候选点的数量N=5;当前模板的匹配阈值Tc=0.9,短时记忆空间模板的匹配阈值Ts=0.8,长时记忆空间模板的匹配阈值Tl=0.8[12],短时记忆空间和长时记忆空间存储的模板数量R=5。
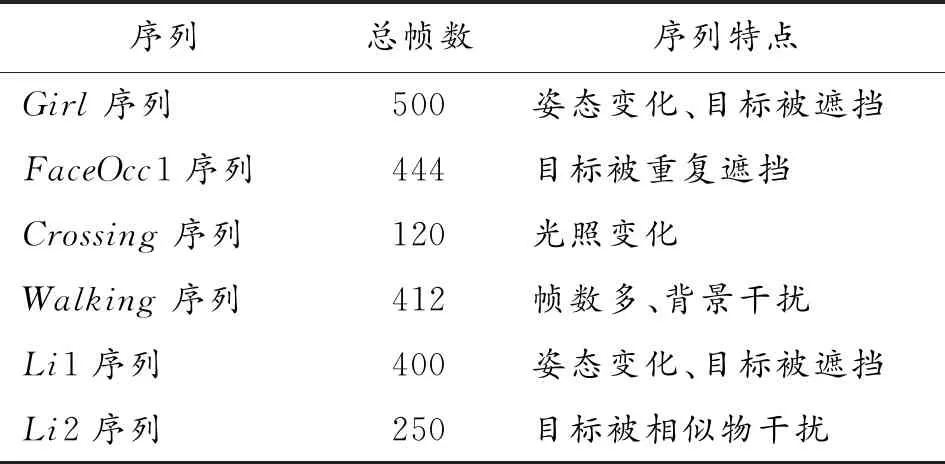
表1 各序列特点
3.2 实验结果与分析
3.2.1定性分析
图5~图10为粒子滤波跟踪算法(PF)、常规STC算法(STC)、压缩感知算法(CT)以及本论文所提出的基于主从记忆空间模型的时空上下文跟踪算法(MSTC)分别对6个视频序列的目标跟踪实验结果。其中,图5是对Girl视频序列跟踪结果图。 由图5可以看出,Girl序列第310帧存在目标姿态变化,CT算法出现跟踪偏移;第420帧以后,目标(女性人脸)出现被遮挡的情况,粒子滤波算法、CT算法、STC算法均错误地跟踪了遮挡物(男性人脸)。同时,本论文提出的算法在目标被遮挡时仍能保持鲁棒性的目标跟踪。
图6是对FaceOcc1序列跟踪结果图。FaceOcc1序列目标(女性人脸)存在被干扰物(书籍)长时或反复遮挡问题,粒子滤波算法和CT算法在第234帧目标被书籍遮挡后出现明显的跟踪偏移;STC算法完全偏移;本论文提出的算法在目标被干扰物遮挡以及再次被遮挡的情况下,仍能准确地跟踪目标。
图7是对Crossing视频序列的目标跟踪结果图。从图7可以看出,Crossing序列在第45帧时出现背景干扰以及光照变化的情况,粒子滤波算法在第45帧开始出现跟踪框偏移,第70帧跟踪到了干扰物(汽车)上;CT算法在第70帧开始出现偏移,第118帧以后跟踪不到目标(行人);STC算法中,在序列第70帧以后跟踪框位置保持不变;本论文所提出的算法到序列最后一帧(120帧),仍可准确地跟踪目标(行人)。
图8是对Walking序列的目标跟踪结果图。Walking序列的背景相对复杂,帧数较多。粒子滤波算法在第343帧及以后均错误地跟踪到图像右方的草坪;STC算法在序列后面几十帧开始出现偏移,目标跟踪出现偏差。相对而言,CT算法和本论文所提出的算法的跟踪效果较为准确。
图9是对Li1序列的目标跟踪结果图,Li1序列中存在多帧目标(人脸)被书本遮挡的情况,粒子滤波算法和常规STC算法均完全丢失目标,CT算法的跟踪结果存在偏差,本论文算法能保持精确的跟踪。
图10是对Li2序列的目标跟踪结果图,Li2序列中存在多帧相似物(人脸)干扰的情况,粒子滤波算法鲁棒性较低,在第94帧即丢失目标;常规STC算法在序列第196帧受到相似物遮挡后,后续帧跟踪到干扰物上,丢失目标;CT算法的跟踪结果存在偏差,本论文算法能保持精确的跟踪。
3.2.2定量分析
利用跟踪精度图,以Girl序列、FaceOcc1序列、Crossing序列、Walking序列为实验对象,对本论文所提出算法及其比较算法的性能进行定量分析。图11为本论文算法与其他算法的跟踪精度对比,其中距离阈值设为20 pixels[14]。
从图11(a)可以看出,在对Girl序列的目标跟踪中,运动目标发生姿态变化且被遮挡时,本论文提出算法的精度可以达到0.99,粒子滤波算法、CT算法、STC算法分别为0.75、0.65、0.9。从图11(b)可以看出,在FaceOcc1序列中,运动目标存在反复遮挡后又重新出现等情况,本论文所提算法的精度达到0.8,粒子滤波算法、CT算法、STC算法分别为0.3、0.5、0.4。从图11(c)可以看出,在Crossing序列中存在光照变化等情况,本论文算法跟踪精度达到1,而粒子滤波算法、CT算法、STC算法分别为0.3、0.95、0.6。从图11(d)的实验结果表明,尽管CT算法和本论文所提出算法对于Walking序列的跟踪效果均较为准确(如图8所示),但CT算法的跟踪精度为0.9,本论文提出的算法精度可以达到1。此外,STC算法分别为0.8,而粒子滤波算法完全偏移。
综上所述,本论文提出算法可在目标被遮挡、姿态突变、短暂消失后重现等条件下仍具有较高的目标跟踪精度。
4 结论
1) 提出了一种基于主从记忆空间模型的时空上下文跟踪算法,通过基于主、从记忆空间模型的模板更新策略,解决了STC算法的模板更新错误的问题。
2) 提出了多置信图候选点,降低了置信图误差带来的影响。
3) 所提出的算法精度高、鲁棒性强,可解决目标被遮挡、姿态突变、短暂消失后重现等目标跟踪问题,在复杂背景、干扰条件下的运动目标跟踪中具有广泛的应用前景。
