基于删除方法构造码长固定的多速率LDPC码

穆锡金，白宝明，贾 倩

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

0 引言

低密度校验(low-density parity-check，LDPC)码是一类逼近信道容量限的线性分组码，是由Gallager于20世纪60年代首先提出的[1]。LDPC 码自提出以后被忽视了很久，直到20世纪90年代，一些学者通过对图码和迭代译码的研究，发现了具有稀疏校验矩阵的线性分组码在迭代译码算法下的性能也能够逼近信道容量限[2]，进而导致了LDPC码的重新发现和广泛研究。由于具有高译码吞吐量、低错误平层、自交织、自校验和码参数设计灵活等优点， LDPC码已经被广泛地应用于蜂窝通信、光纤通信、深空通信、卫星数字广播和大数据存储等多种系统中[3]。

实际的无线通信系统往往需要码率可变的LDPC码来适应无线信道的时变特性，同时为了降低系统的整体复杂度，多个码率的码应该能用一套编译码器实现[4-5]。码率可变的LDPC 码成为当下研究热点，其主要包括两类：码长固定的多速率LDPC(Multi-rate LDPC，MR-LDPC)码和信息位长度固定的速率兼容LDPC(Rate-compatible LDPC，RC-LDPC)码，其中MR-LDPC码是在固定码长的条件下，通过改变信息位长度实现码率可变的；而RC-LDPC码是在固定信息位长度的条件下，通过改变码长实现码率可变的。可以通过打孔和缩短的方法构造码率范围较广的RC-LDPC码[6-8]，其优化的打孔和缩短模式保障了所构造的码具有较好的性能。除了打孔和缩短方法外，扩展也是一种构造RC-LDPC码的有效方法，基于该方法构造的码具有较广的码率范围和较好的性能[11]。MR-LDPC码的码长不随着码率的变化而改变，因此适合于一些需要码长固定的场景，如多层编码调制系统等。Casado等人利用行合并的方法构造了一类MR-LDPC码，所得到的码在各个码率下都具有较低的错误平层[12]。王琪等人通过修正渐进边增长的方法构造了一类具有准循环结构的MR-LDPC码，所构造的码具有低复杂度的编译码结构[13]。

本文基于删除方法构造了一类码长固定的多速率LDPC码。与此同时，利用LDPC码的叠加构造整体设计所有码的校验矩阵，其构造的码易于编译码器硬件实现，并且能够用校验矩阵直接编码。仿真结果表明，所构造的码在多种码率下都具有较好的瀑布区和平层区性能。

1 删除方法

删除是一种构造多速率码的有效方法，其过程是先构造一个高码率母码，然后在保持码长不变的条件下减少高码率母码的信息位数目，进而获得低码率的码。图1和图2分别展示了应用删除方法得到低码率LDPC码时校验矩阵和Tanner图的变化，可以看到，校验矩阵的列数没有变化，但行数增加了；Tanner图中对应信息比特的变量节点数目减少了，但变量节点的整体数目没有变化，与此同时，校验节点的数目增加了。

图1 校验矩阵的变化

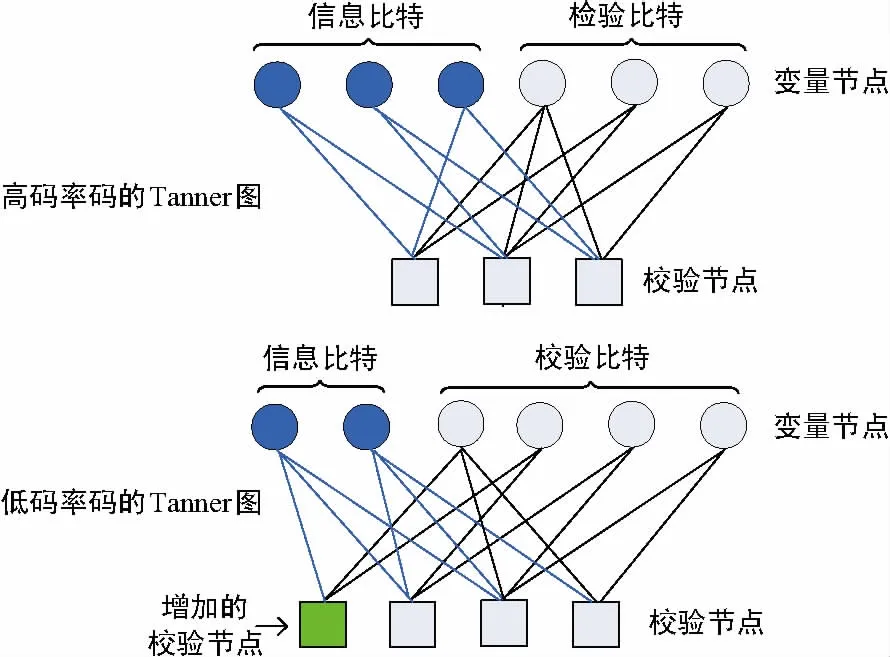
图 2 Tanner图的变化

2 LDPC码的叠加构造

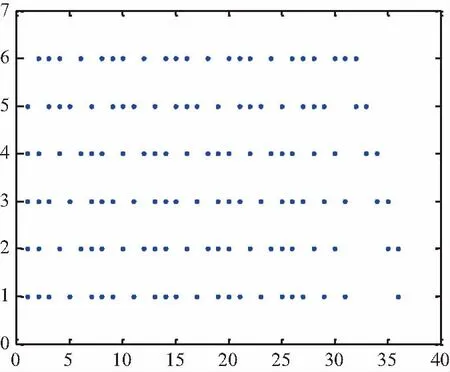
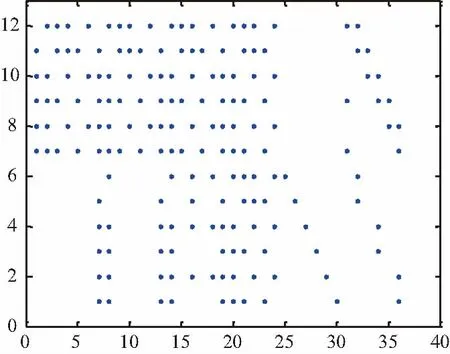
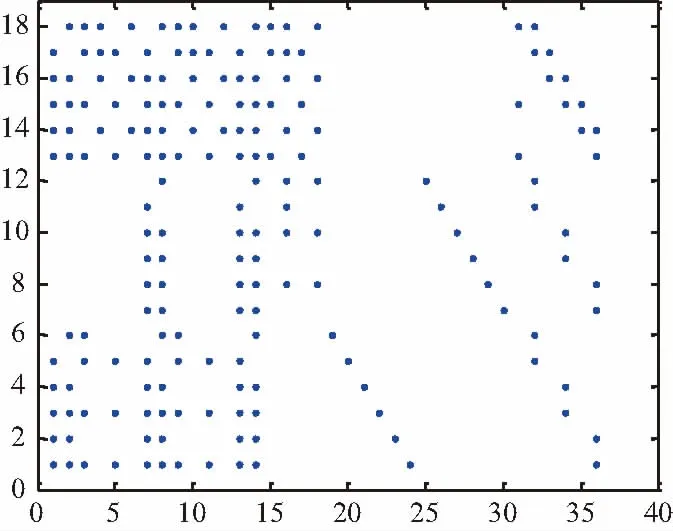
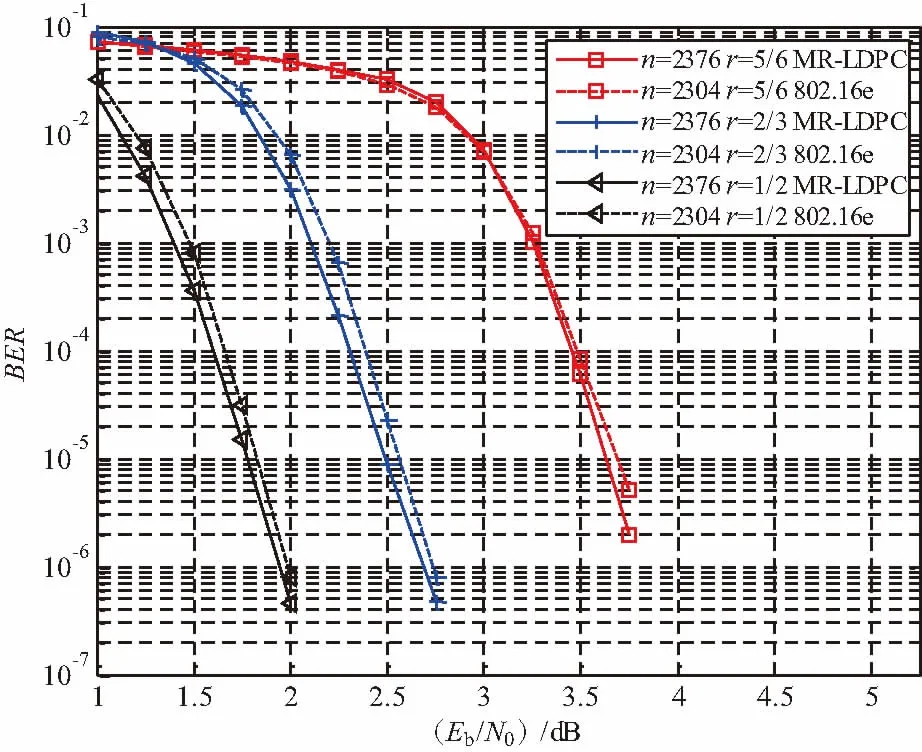
LDPC码的叠加构造最早是由Lin等人于2001年提出的[14]。构造过程涉及了一个大小为M×N的基矩阵B=[bm,n]0≤m

Hmask=Z⊗H=[zm,n·Am,n]0≤m

(1)

当zm,n=1时，zm,n·Am,n=Am,n；当zm,n= 0时，zm,n·Am,n=O，即一个全零矩阵。其中二元矩阵Z被称为掩模矩阵，经过掩模操作后得到的矩阵阵列Hmask的零空间即可定义一个LDPC码。

3 基于删除方法构造MR-LDPC码

按照删除的过程，首先构造一个具有系统形式的高码率LDPC码，为了在码长固定的条件下降低码率，需要在减少信息位的同时增加校验位。其中的难点在于：如何在保持已有高码率LDPC码校验矩阵结构的前提下，实现信息位的减少和校验位的增加。针对以上难点，采用LDPC码的叠加构造来整体设计所有码的校验矩阵。

假设要构造的MR-LDPC码的码集合为{C1(n,k1),C2(n,k2),…,CS(n,kS)}，其中k1>k2>…>kS。码Cs(n,ks)对应的码长为n，信息位长度为ks，码率为rs=ks/n，校验矩阵为Hmr,s，其中s∈{1,2,…,S}。图3展示了MR-LDPC码校验矩阵的设计流程，首先基于有限域设计叠加构造中的基矩阵B；然后用循环置换矩阵(Circulant Permutation Matrix，CPM)作为叠加矩阵集合中的成员矩阵，并对基矩阵进行扩展操作，得到矩阵阵列H；分别选择H中的部分行阵列，构成矩阵阵列H1,H2,…HS，将H1,H2,…HS分别与给定的掩模矩阵Z1,Z2,…ZS进行掩模操作，最终得到各个码率的校验矩阵Hmr,1,Hmr,2,…,Hmr,S。

图 3 MR-LDPC码校验矩阵的设计流程

可以利用有限域来设计基矩阵[15]，假设GF(q)是包含q个元素的有限域，α为GF(q)的一个本原元，GF(q)中所有的元素可以表示为α幂次的形式，其中0=α-∞,1=α0,α1,α2,…,αq-2，S1={αi0,αi1,…,αiM-1}和S2={αj0,αj1,…,αjN-1}是GF(q)的2个子集，其中im,jn∈{0,1,…,q-2},0≤m

(2)

式中，αcm,n=αim-αjn,0≤m

扩展操作是将基矩阵B中的元素αcm,n替换成大小为(q-1)×(q-1)且循环系数为cm,n的CPM，经过扩展操作可以得到矩阵阵列H，分别从H中选择前M1,M2,…,MS个行阵列就可得到矩阵阵列H1,H2,…HS，其中Ms=(n-ks)/(q-1)。

掩模矩阵是由“0”元素和“1”元素组成的二元矩阵，可以通过计算机优化搜索或代数理论设计的方法得到。将H1,H2,…HS分别与给定的掩模矩阵Z1,Z2,…ZS进行掩模操作，得到各个码率的校验矩阵Hmr,1,Hmr,2,…,Hmr,S，具体过程为：

Hmr,s=Zs⊗Hs=[zm,n·Am,n]0≤m

(3)

式中，当zm,n=1时，zm,n·Am,n=Am,n；当zm,n= 0时，zm,n·Am,n=O。

4 数值结果

本节根据上述方法构造了MR-LDPC码，并通过数值仿真对所构造的码的性能进行检测和验证，本节的所有仿真都是假设码字经过二进制相移键控(Binary Phase Shift Keying，BPSK)调制后在加性高斯白噪声(Additive White Gaussian Noise，AWGN)信道中传输，译码器采用和积译码算法(Sum-product Algorithm，SPA)，最大译码迭代次数为50次。

所构造码的码长为2376比特，码率为5/6、2/3、1/2。选择有限域GF(67)，本原元α= 2，集合S1包含18个从GF(67)中随机选取的元素，集合S2包含36个从GF(67)中随机选取的元素，根据S1和S2可以构造大小为18×36的基矩阵B。对基矩阵B进行扩展操作可以得到矩阵阵列H，分别从H中的选择前6、12、18个行阵列就可以得到矩阵阵列H1,H2,H3。

图4、图5及图6分别展示了给定的掩模矩阵Z1，Z2，Z3的散点图。

图4 掩模矩阵Z1的散点图

图5 掩模矩阵Z2的散点图

图6 掩模矩阵Z3的散点图

将H1,H2,H3分别与给定的掩模矩阵Z1,Z2,Z3进行掩模操作，最终得到各个码率的校验矩阵Hmr,1,Hmr,2,Hmr,3。

图7展示了所构造的MR-LDPC码的误比特率(Bit Error Rate，BER)性能。

图7 所构造的MR-LDPC码的性能

可以看到，所构造的码在各个码率下都具有较好的瀑布区性能，并且在BER等于10-6时没有明显的错误平层。图7还展示了所构造的MR-LDPC码与IEEE 802.16e标准[16]中具有相似码率和码长的LDPC码之间的性能比较，可以看到，本文所构造的MR-LDPC码具有更好的性能。

5 结束语

基于删除方法构造了码长固定的多速率LDPC码，在码长不变的前提下，通过减少高码率母码信息位数目得到低码率码。通过叠加构造法整体设计了不同码率的LDPC码的校验矩阵，最终构造的码具有易于编译码器硬件实现的准循环结构，并且能够用校验矩阵直接编码。仿真结果表明，与IEEE 802.16e标准中具有相似码率和码长的LDPC码相比，所构造的码在较大的码率范围内都具有较好的瀑布区和平层区性能。