散射通信中的LDPC码性能分析与优化

戴精科，林开亮

(1.火箭军工程大学，陕西 西安 710025； 2.西北农林科技大学，陕西 西安 712100)

0 引言

散射通信利用对流层或电离层中不均匀介质对电磁波产生的散射进行通信，其信道具有典型的衰落特征，需要引入信道编码提高传输可靠性。低密度奇偶校验(Low-Density Parity-Check，LDPC)码作为一种性能逼近香农极限的先进信道编码技术，具有极强的纠错能力，因此将其应用于散射通信可提高系统的抗衰落能力，改善通信质量[1-3]。

由于散射通信的超视距和多径传播特性，其信道一般建模为瑞利衰落信道，即接收机只接收到散射信号分量而没有直射信号。文献[4]利用密度进化[5-6](Density Evolution，DE)理论确定了LDPC码在瑞利衰落信道中的性能界，而文献[1-2]则对有限长LDPC码在散射通信系统中的性能进行了仿真。近年来，有学者将散射信道建模为低莱斯因子衰落信道[7-8]，即通信中不仅存在反射信号，还存在一个较小的“直射”分量。文献[9]证明了莱斯信道满足对称性，给出了译码稳定性条件并和文献[10]分别利用密度进化和离散密度进化[11](Discretized Density Evolution，DDE)分析LDPC码在莱斯信道中的性能并进行了度分布优化。文献[7-8]则针对低莱斯因子信道进行了LDPC码误码率仿真。但是DE、DDE以及实际码字的蒙特卡洛仿真需要很大计算量且非常费时，在搜索优化的不规则码时更是如此[12]。

Lehmann针对上述缺点，提出一种基于高斯近似的方法[13]，推导出了LDPC码在加性高斯白噪声和瑞利衰落信道下的误码率闭合表达式，在误差可接受的情况下极大降低了计算复杂度。文献[14-15]将该方法推广至采用分集合并的瑞利和Nakagami衰落信道，推导误码率闭合表达式并与实际码字性能进行了比较。但是，Lehmann方法需要得到信道输出消息(对数似然比LLR)的闭合表达式，而莱斯信道的初始LLR只存在积分形式[9]，难以得到误码率闭合表达式。因此，本文将Lehmann方法与快速傅里叶变换相结合，推导出LDPC码在莱斯衰落信道中的误码率。通过仿真发现，该误码率与实际码字性能非常吻合，且相应的MATLAB程序时间只有DE方法的百分之一到千分之一。对差分进化算法进行修改，解决了度分布参数无效问题，并获得了优化的不规则码，在误码率为10-6时所需信噪比相对规则码要低0.5～0.7 dB。

1 系统模型

系统采用BPSK调制和相干解调方式。设传输符号x∈{0,1}，调制信号映射为w=1-2x，则解调器输出y的条件概率密度函数(Probability Density Function,PDF)为[9]：

(1)

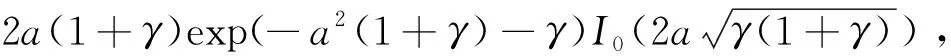
信道输出的对数似然比为：

在全零假设[5](即x≡0)下对式(1)进行变量代换则可得到u0的条件PDF：

(2)

将其对a取平均有：

(3)

式中，I0(x)为零阶修正的贝塞尔函数。

2 LDPC编码系统误码率

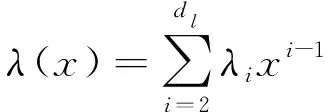
2.1 校验节点

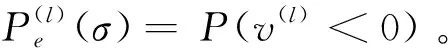
(4)

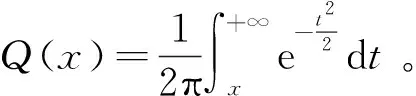
2.2 变量节点

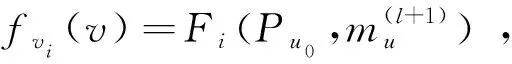
(5)

第l+1次迭代结束时的错误概率为：

(6)

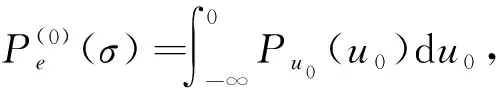
3 码优化

但该算法在实现时会出现下列问题：① 由于L维向量元素都是随机选择的(取值范围限定在区间[0,1])，在计算参数λ2、ρ2和λdl时并不能保证它们的取值也在区间[0,1]中；② 在进行差分进化时“新”向量组由“前一代”向量组的线性组合生成，参见文献[4]中式(27)，因此也不能保证生成的新向量取值都在区间[0,1]中。

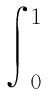
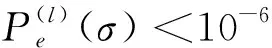
表1 优化后不规则LDPC码的度分布

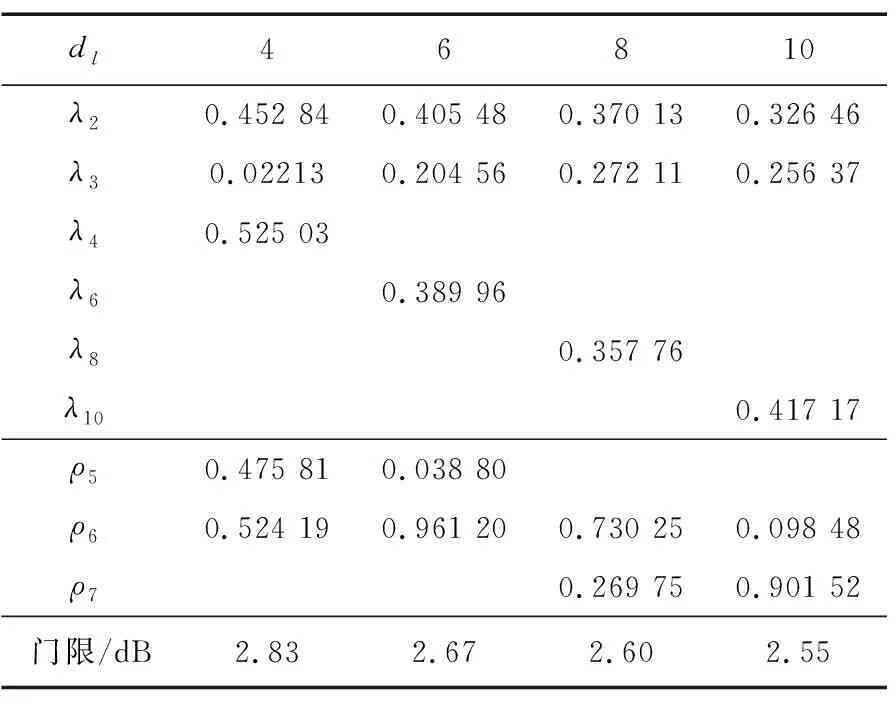
dl46810λ20.452 840.405 480.370 130.326 46λ30.022130.204 560.272 110.256 37λ40.525 03λ60.389 96λ80.357 76λ100.417 17ρ50.475 810.038 80ρ60.524 190.961 200.730 250.098 48ρ70.269 750.901 52门限/dB2.832.672.602.55

4 仿真结果

本节对LDPC码在散射信道中的性能进行仿真和比较，莱斯因子分别设为0 dB(图1)和6 dB(图2)，所用码字为1/2码率的(3,6)规则码(reg)和表1中dl=10的不规则码(irreg)，Sim表示码长为104实际码字误码率仿真，GA代表本文基于高斯近似推导的理论误码率，DE代表利用密度进化得到的译码门限。

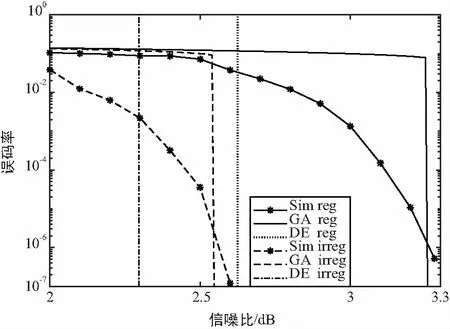
图1 莱斯因子0 dB信道中LDPC码的误码率性能

从仿真结果可以看出，在高信噪比区域理论计算和实际码字仿真获得的性能非常接近，当误码率在10-6附近时两者的误差在0.01～0.2 dB以内，例如，莱斯因子为0 dB时规则码的理论误码率小于10-6时所需的信噪比为3.27 dB，而仿真结果约为3.28 dB；莱斯因子为6 dB时不规则码所需的信噪比为1.75 dB，而仿真结果约为1.89 dB。这说明本文推导的误码率非常准确地预测了实际码字的性能。DE获得的译码门限最低，因为其代表了码长趋向于无穷大时的性能，但这在实际通信中是不可能实现的，GA方法能够对有限长码字的性能进行快速和有效的估计[14]，因此更有实际意义。通过比较Matlab程序运行时间，DE方法耗时是GA的数百倍。另外，本文得到的不规则码性能明显优于规则码，在两种信道条件下实际码字的增益约为0.7 dB和0.5 dB。

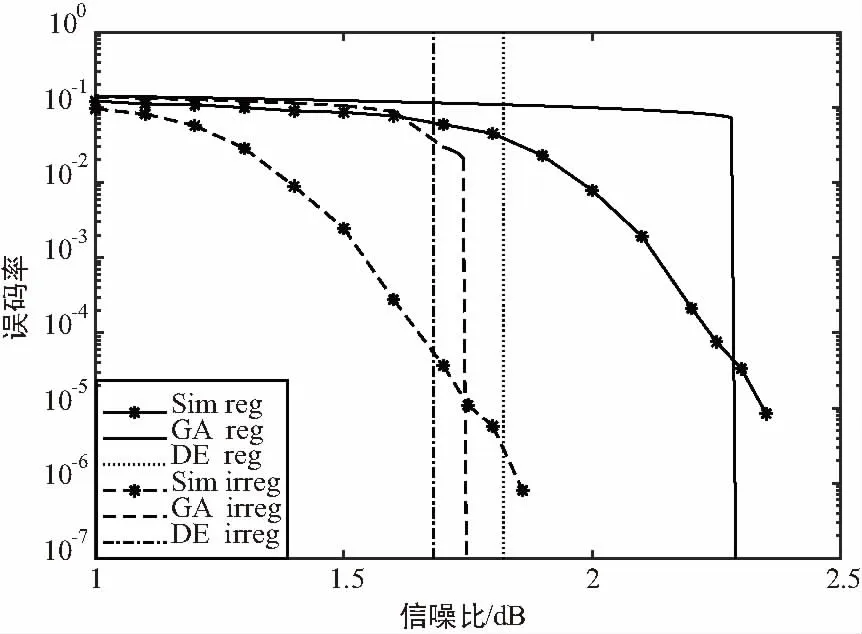
图2 莱斯因子6 dB信道中LDPC码的误码率性能

5 结束语

本文将散射信道建模为低莱斯因子衰落信道，分析了LDPC码在该信道中的性能并对其度分布进行了优化设计。基于高斯近似和快速傅里叶变换推导了码字的理论误码率，仿真结果表明该值与实际码字性能非常接近，且计算量远小于密度进化方法。对差分进化算法进行修改，避免了搜索过程中出现的度分布值无效问题，且优化的不规则码在相同信道条件下相对规则码有0.5～0.7 dB增益。