衰落信道下的信源数目估计方法

王艳温,郭 楠

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.陆军航空装备发展办公室，北京 100012)

0 引言

信源数目估计[1]对盲信号分离和超分辨测向的性能影响较大。盲信号分离方法[2-3]一般是以信源数目已知为前提，但实际应用中信源数目未知，需要进行估计。当信源数目欠估计时，只能分离出部分信号，导致信号信息的丢失；当信源数目过估计时，导致盲分离算法失效，无法正确地分离信号。因此信源数目估计在盲信号分离中起到了十分重要的作用，它直接关系到盲分离算法的正确性和稳定性。在超分辨测向中[4-5]，信源数目估计也是必须的。信源数目过估计时，源信号子空间的维数高于实际值，使得之后计算出的空间谱出现伪峰；源信号数目欠估计时，源信号子空间的维数低于实际值，使得之后计算出的空间谱的谱峰消失；这样导致了源信号子空间与噪声信号子空间同样不再正交，最终估计的空间谱与实际的信号之间出现较大偏差。

信源数目估计不单单在盲信号分离和超分辨测向中有重要的作用，在战场、刑侦、检测及图像等实际问题中，同样具有很大的应用价值。而现有较成熟的基于信息论、最大似然及线性预测等信源数目估计方法均是利用白噪声信号模型推导出来的，仅适用于白噪声条件。但在实际中，由于多径干涉、外界环境等各种因素的影响，导致接收信号的幅度相位出现较大程度的抖动，接收信道[6-7]不再是理想的高斯白噪信道，而变成衰落信道。在衰落信道下现有信源数目估计方法的性能下降严重。因此，对衰落信道下的信源数目估计方法进行研究有着十分重要的理论和实际意义。

1 瑞利平坦衰落信道下信源数目估计方法

对于瑞利平坦衰落信道[8-11]下的信源数目盲估计，其问题的关键在于利用噪声分布已知的特性来进行判断。较为成熟的算法有AIC、MDL和PET算法[12-13]。AIC、MDL算法虽然不需要人为设定判决门限，但是其利用噪声满足高斯分布的特性，估计收敛性较差。PET算法在性能上较之前两种有很大改进，但是它需要人为设定判决门限。根据这些经典算法已有的固有缺陷，本文提出了基于Wishart矩阵[14-15]最大特征值分布特性的估计算法(WME)，该算法利用高斯随机矩阵特征值以较快的收敛速度渐进服从精确的TW分布这一特点，进行信源数目盲估计，并可获得较好的性能。

利用阵元个数为M的天线阵列接收数据计算协方差矩阵，对协方差矩阵进行特征值分解得到特征值并按降序排列，利用随机矩阵理论构造检测统计量，求解判决门限，确定检测统计量属性，估计得到信源个数N。

天线阵列接收数据的协方差矩阵R：

式中，E[·]表示数学期望，上标H表示复共轭转置，X(i)表示第i次快拍的天线阵列接收信号，L表示快拍数。

对协方差矩阵R进行特征值分解，得到M个特征值，满足：

λ1>λ2≥…≥λM-1>λM。

设置虚警概率Pfa，并令k=1；

计算检验统计量Uk：

计算判决门限γk：

式中，FTW2(x)表示第二类Tracy-Widom分布函数[16]的逆函数，μM-N,L和εM-N,L为归一化参数，其表达式如下：

在计算判决门限时，需要计算分布函数FTW2(x)的逆函数。目前在数学领域，Tracy-Widom分布函数的闭合表达式是很难得到的。在实际工程应用中，FTW2(x)的逆函数计算结果大多是通过查表的方式获得。

判决：

如果Uk<γk，则lk∈Ls，k=k+1，重新计算检验统计量Uk+1；

如果Uk>γk，则信源个数N=k-1。

2 频率选择性衰落信道下信源数目估计方法

以上所提到的一系列经典算法包括WME算法都只适用于瑞利平坦衰落信道环境，而频率选择性衰落信道[17-19]更贴近于实际的通信环境，因此有必要对在频率选择性衰落信道条件下的信源数目估计算法进行研究。基于此提出了一种基于对噪声功率精确估计的假设检验[20]估计算法(FKN)。具体实现步骤如下：

步骤1：计算天线阵列接收数据X(t)的协方差矩阵R：

步骤2：构造检测统计量

Ⅰ 对协方差矩阵R进行特征值分解，并将分解得到的特征值按降序排列：λ1>λ2≥…≥λM-1>λM，其中,λk表示按照降序排列的第k个特征值，1≤k≤M。

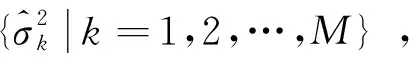
步骤3：求解判决门限值γk

γk=F-1(1-Pfa)εL,Nr-k+μL,Nr-k，

式中，F-1(1-Pfa)表示第二类Tracy-Widom分布的逆累积分布函数，Pfa表示预先设定的虚警概率，归一化系数为：

步骤4：确定检测统计量属性

如果检测统计量Uk大于判决门限γk，则将检测统计量Uk判定为信号统计量；

如果检测统计量Uk小于判决门限γk，则将对应检测统计量Uk判定为噪声统计量。

步骤5：确定信源数目N。

3 仿真验证分析

3.1 瑞利平坦衰落信道

在瑞利平坦衰落信道条件下，对信源数目估计经典算法AIC、MDL、PET与所提WME算法的正确估计概率进行了对比。仿真条件如下：

·信源数目：4；

·阵元数：16；

·噪声特性：瑞利分布色噪声；

·信噪比范围：-10～5 dB；

·采样点数：50～600；

·蒙特卡洛次数：1 000次。

WME算法的估计概率随信噪比变化曲线如图1所示，WME算法的估计概率随采样点数变化曲线如图2所示。

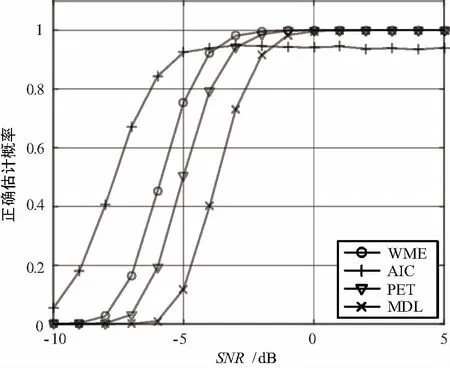
图1 WME算法估计概率随信噪比变化曲线

由图1可以看出，WME算法在低信噪比条件下的正确识别率要高于PET和MDL算法，稍逊于AIC算法，但是由于AIC算法是非一致算法，在较高信噪比条件下无法收敛于1。

图2 WME算法估计概率随采样点数变化曲线

由图2可以看出，WME算法在样本数40以上的性能优于MDL算法，在更少的样本数下优于AIC和PET算法。

3.2 频率选择性衰落信道

在频率选择性衰落信道条件下，对提出的FKN信源数目估计算法的性能进行了仿真分析。仿真条件如下：

·工作频段：1.5～30 MHz；

·信源数：2～4；

·阵元数：8；

·信道条件：多径数为3、最大延时≤0.05 ms、最大反射系数为1的频率选择性衰落信道；

·信噪比：-8 ～8 dB；

·采样点数：10～300；

·蒙特卡洛次数：1 000次。

FKN算法的估计概率随信噪比变化曲线如图3所示，FKN算法的估计概率随采样点数变化曲线如图4所示。

图3 FKN算法估计概率随信噪比变化曲线

图4 FKN算法估计概率随采样点数变化曲线

由图3可以看出，在频率选择性衰落信道中FKN算法在低信噪比条件下能够达到较高的估计概率，且随着信源数目的增加，达到估计概率100%所需的信噪比越高。

由图4可以看出，在频率选择性衰落信道条件下，FKN算法的估计概率高于AIC和MDL，且样本数在50以上就能达到100%的估计概率。

4 结束语

在瑞利平坦衰落信道和频率选择性衰落信道中，针对现有信源数目估计方法在低信噪比条件下估计效果差、高信噪比条件下容易出现过估/欠估、算法收敛较慢的特点，提出了具有快速收敛特性的基于小样本的信源数目估计算法，通过仿真分析所提算法具有较好的估计性能。本文的研究成果可用于短波、超短波等侦测系统的盲信号分离和测向处理中，能够有效提高侦测性能。