非概率响应面界限法在桥梁可靠性评估中的应用

边晓亚， 陈旭勇， 陈 谦,2， 樊建平

(1. 武汉工程大学 土木工程与建筑学院， 湖北 武汉 430074； 2. 武汉市汉阳市政建设集团公司， 湖北 武汉 430050；3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

桥梁作为运输线路的咽喉要道和交通枢纽，其可靠性与人民的生命财产安全息息相关。技术状况不佳的桥梁不仅会对车辆通行造成极大的隐患，而且还会导致重大的经济损失。因此，对桥梁进行可靠性评估就显得尤为重要。

桥梁评估是指利用影响桥梁结构的各种作用及其在结构上产生的效应，通过检测、计算和分析，对桥梁的病害状况、承载能力、正常使用功能及损伤程度进行鉴定[1]。现有的桥梁结构可靠性评估方法有外观调查法、荷载试验法、专家经验法及概率可靠性法[2]。概率可靠性是指在大样本空间情况下，已知精确的概率密度分布函数或隶属函数，通过概率统计方法计算结构的可靠度或可靠性指标[3]。但在实际工程中，足够大的样本空间、精确的概率密度函数或隶属函数往往不易获得或不能获得。

针对概率可靠性理论的局限性，Qiao[4]用凸集模型处理结构分析和设计中的不确定性问题，讨论了当前非概率可靠性的局限性，提出了一种新的非概率可靠性模型，并证明了所提出模型的可行性。Meng等[5]提出了一种基于解耦策略的非概率可靠性优化算法，进一步建立了新的非概率可行性准则。Li等[6]提出了一种在结构振动主动控制系统中具有未知但有界参数的非概率可靠性分析方法，讨论了一种新的非概率可靠性度量指标，用于确定基于面积比的可靠性概率。陈旭勇和樊建平[7]提出了基于非概率可靠性的改进的一维优化算法，并且成功地运用到桥梁的评估中，为在役桥梁的简化评估提供了理论依据。Peng等[8]对含有概率不确定变量和非概率有界不确定变量的层板进行了可靠性分析与优化，证明了考虑非概率不确定性变量可以得到更保守的结果。陈旭勇等[9]针对结构复杂的拱桥，引入非概率可靠性理论进行可靠性评估，验证了非概率可靠性评估的合理性。Li和Chen[10]利用凸集模型描述不确定参数，在凸集模型和功能函数的基础上建立非概率可靠性模型，利用梯度投影法求解非概率可靠性指标，并证明利用非概率可靠性进行桥梁评估更合理、更经济。Wang等[11]提出了一种新的非概率时变可靠性指标，对含裂纹工程结构的安全寿命进行了准确评估。Wang等[12]结合非概率凸集模型，提出了混合安全可靠性的数学定义，并对复杂的工程实例进行强度和刚度准则的数值计算。

虽然常见的非概率可靠性指标的算法已有很多，诸如一维优化算法[13]、改进的一维优化算法[7]、梯度投影法[14]、全局最优解法[15]和空间搜索法[16]等。但这些方法均基于功能函数已知情况下求解非概率可靠性指标，而实际工程中功能函数往往不易得到。面对这样的困境，本文针对在功能函数未知情况下非概率可靠性指标不易求解的问题，引入基于区间模型的非概率响应面界限法对在役桥梁进行可靠性评估。

1 基于区间模型的非概率可靠性指标

M=g(x)=g(x1,x2,…,xn)

(1)

当g(x)为xi(i=1,2,…,n)的连续函数时，M也为区间变量。按结构非概率可靠性理论，称超曲面g(x)=0为失效面。当g(x)<0时，结构处于失效状态；当g(x)>0时，结构处于安全状态。

设M的均值和离差分别为Mc和Mr，则非概率可靠性指标为[13]：

(2)

从几何意义上讲，非概率可靠性指标η为按无穷范数度量，从坐标原点到失效面的最短距离。从物理意义上讲，非概率可靠性指标η代表了结构的可靠性系数。

产品结构管理是通过物料清单，把产品的所有工程数据和文档联系起来，实现对产品数据的有效组织、控制和管理，为各阶段，各部门和各类技术及管理人员提供信息服务。

2 非概率响应面界限法

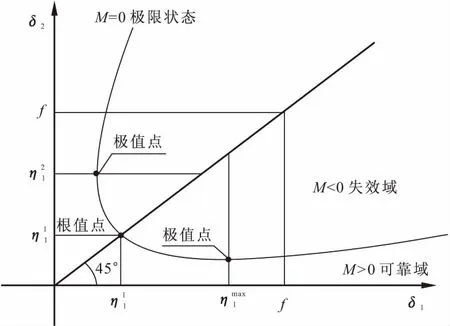
图1 第一次迭代过程

图2 第n次迭代过程

上述界限法基本步骤归纳如下：

(2)根据初始参数值，利用有限元方法及Matlab等软件得到2n+1个函数值M，构造二次型功能函数方程，求解线性方程组，得到2n+1个待定系数a，bi，ci(i= 1, 2,…,n)，即求得初始响应面函数M=g(x)，将xi(i= 1, 2,…,n)标准化，得到正则化的极限状态函数G(δ)。

ηn-ηn-1<εηn-1,ε=0.0001

(3)

3 实例分析

现有一座三跨PC连续刚构桥，桥梁跨径为75+130+75 m，下部结构为双薄壁柔性墩[18]。

3.1 评估流程

基于非概率响应面界限法的桥梁可靠性评估流程如图3所示。

图3 可靠度评估流程

3.2 确定控制参数

研究表明，预应力钢筋和混凝土抗压强度都是影响桥梁极限承载力和结构性能的重要因素[19]。因此，选取混凝土的抗压强度C及预应力筋截面面积As为变化参量进行分析。普通混凝土分为14个等级[20]，其中C50的混凝土是指50 MPa≤C≤ 55 MPa，因此将混凝土抗压强度区间优化为C∈[50, 55] MPa。公称直径为15.24 mm的钢绞线公称直径允许误差为[-0.2, +0.4] mm[21]，公称直径为d∈[15.04, 15.64] mm，根据公称直径计算预应力筋截面积As的区间估计，As∈[138, 144] mm2。

3.3 有限元模型建立

通过Midas软件建立有限元模型(见图4)，分析可知中跨(跨径为130 m)的跨中截面弯矩最大。因此，以中跨的跨中截面为控制截面，对结构进行非概率可靠性分析。

图4 有限元模型

3.4 承载能力极限状态评估

令f=2，模型的初始参数及其利用Midas求得的抗力R和效应值S如表1所示。

表1 初始参数值

根据以上参数，利用本文提出的非概率响应面界限法进行非概率可靠性指标的求解，拟合的功能函数为：

M=1.21×10-4-4.83×103x1+1.04×103x2+

正则化功能函数后，求解得到非概率可靠性指标η=(3.225, 287.221, 16.356, 1.168)，而满足条件f<2的最大值为1.168，即η=1.168。再令η=1.168，进行第一次迭代计算。第一次迭代后参数值如表2所示。

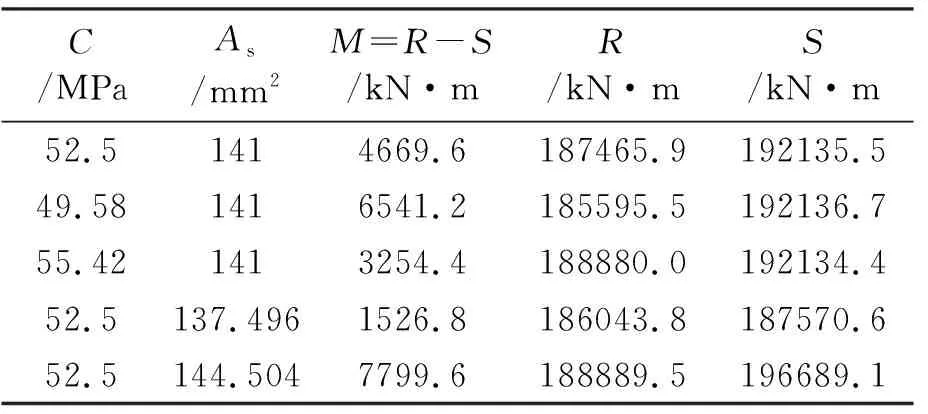
表2 一次迭代后参数值

根据以上参数，利用非概率响应面界限法进行非概率可靠性指标求解，拟合的功能函数为：

M=-2.86×104-3.37×103x1+1.04×103x2+

正则化功能函数后，求解得到非概率可靠性指标η= (4.206, 285.896, 23.976, 1.198)，而满足条件η<1.168的值不存在，即η=1.168=ηmin，η=2=ηmax。再令f=1.168和f=2分别选取迭代点，进行第二次迭代计算。第二次迭代后参数值如表3所示。

表3 二次迭代后参数值

根据以上参数，利用非概率响应面界限法进行非概率可靠性指标求解，拟合的功能函数为：

M=-9.76×104-2.86×103x1+1.82×103x2+

正则化功能函数后，求解得到非概率可靠性指标η= (6.041, 49.325, 41.241, 1.15751)，而满足条件η<1.168的值为1.15751，则η=1.15751。再令f=1.15751，进行第三次迭代计算。第三次迭代后参数值如表4所示。

表4 三次迭代后参数值

根据以上参数，利用非概率响应面界限法进行非概率可靠性指标求解，拟合的功能函数为：

M=1.1185×108-5.2234×105x1-1.4187×106x2+

正则化功能函数后，求解得到非概率可靠性指标η=(1.184, -1.248, 1.289, 1.15762)，而满足条件1.15751<η<1.168的值为1.15763，且(1.15762-1.15751)/1.15751<10-4，满足收敛条件，最终的非概率可靠性指标η=1.15762>1，结构在承载能力极限状态下处于可靠状态。

4 结 论

本文提出了可以高效求解非概率可靠性指标的非概率响应面界限法，并建立了适用于在役桥梁的非概率可靠性评估方法。以一座三跨PC连续刚构桥为例，在功能函数未知，已知参数较少的情况下，利用非概率响应面界限法及非概率可靠性评估流程，对桥梁进行非概率可靠性评估，快速地求得了非概率可靠性指标，η=1.15762>1。此结果表明该桥梁在承载能力极限状态下是可靠的，也证明了提出的非概率响应面界限法及可靠性评估流程在在役桥梁可靠性评估中的可行性。因此，本研究提出非概率响应面界限法及非概率可靠性评估流程为在役桥梁的可靠性评价提供了一种新的途径。