基于迭代学习控制的永磁同步电机转矩波动抑制策略
2018-08-22刘亚清邓惟滔
刘亚清,邓惟滔
(1.巴陵石化公司合成橡胶事业部,岳阳 414000;2.湖南理工学院信息科学与工程学院,岳阳 414000)
文章编号:1007-1423(2018)22-0014-06DOI:10.3969/j.issn.1007-1423.2018.22.003
0 引言
永磁同步电机具有功率密度高、效率高、鲁棒性强和结构简单等优点,因而在工业生产中得到广泛应用[1-4]。但空间磁场分布非正弦、齿槽效应和电流检测误差等因素引发的转矩波动问题严重影响了调速系统的控制精度,限制了永磁同步电机在高性能直驱系统的应用[5]。
为了抑制永磁同步电机的转矩波动,国内外学者提出了各种方法,大体可分为两类。第一类是从电机设计角度,主要有斜槽或斜极和改进绕组分布等[6,7]。这类方法增加了电机设计与制造过程的复杂性,从而最终增加了电机的成本。第二类是从控制系统设计角度,通过优化控制策略来减小转矩波动。早期的文献中常采用电流波形优化(Current Profiling)的方法[8],关键在于获取转子位置及相应转矩波动量的先验关系,属于开环补偿方式。文献[9]基于傅里叶变换分析电机反电势的各次谐波,并由此计算出产生恒定转矩需要的电流波形,从而通过注入谐波电流达到抑制转矩波动的效果。文献[10,11]在永磁同步电机矢量控制系统基础上,将迭代学习控制器(ILC)引入q轴电流参考值生成环节,通过ILC对周期性信号的学习能力,实现q轴电流参考值的修正,获得平滑转矩控制。但是,上述策略需要转矩的测量或估算,因此控制系统的成本和复杂性有所增加。
针对永磁同步电机转矩波动问题,本文提出一种参数自适应迭代学习控制算法构建系统转速环控制器。该策略通过记忆机制积累控制经验,实现对下一周期控制信号的调整,产生适当的q轴电流参考信号,达到抑制转矩波动的目的。同时对控制器参数的在线调节,兼顾系统的稳态性能与动态性能。该控制器兼有PI控制和迭代控制的优点且无需反馈转矩信号,利于简化控制系统结构。
1 永磁同步电机数学模型及转矩波动分析
1.1 迭代学习控制原理
迭代学习控制(Iterative Learning Control,ILC)是一种基于记忆机制的无模型控制方法,它的主要思想是利用控制系统先前的控制经验,根据所测的系统实际输出和给定目标轨迹的偏差修正不理想的控制信号,使被控对象产生期望的运动。其基本结构如图1所示。
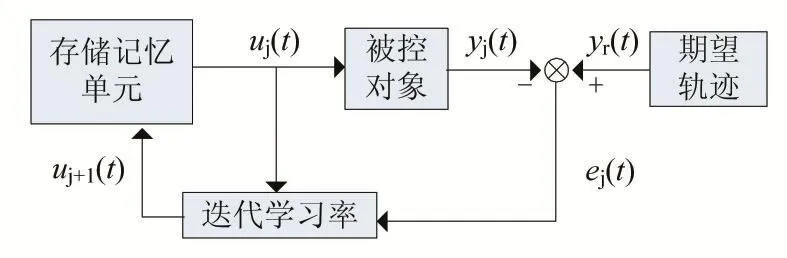
图1 迭代学习控制系统框图
图1中迭代学习率利用当前迭代周期的控制信号及系统输出误差计算出下一迭代周期的控制信号,并存入存储记忆单元。迭代学习率可表示为:

式中,uj(t)、uj+1(t)为控制信号;ej(t)=yr(t)-yj(t),ej+1(t)=yr(t)-yj+1(t)为误差信号;yr(t)为给定信号;yj(t)、yj+1(t)为反馈信号;下标j、j+1表示迭代周期数。当式(1)中含有ej+1(t)时称为反馈型迭代学习控制;当仅含有ej(t)时称为前馈型迭代学习控制,图1所示即为前馈型迭代学习控制。为提高响应速度,本文采用反馈型迭代学习控制,并且学习率中不包含ej(t),以简化控制器的结构及设计。
采用反馈型迭代学习控制算法时,有:
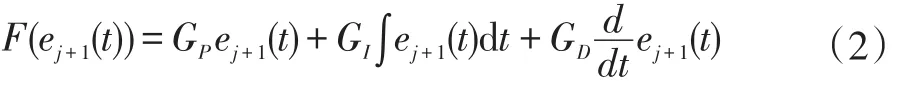
式中的学习增益GP、GI和GD不同为零时,可构成P型、PI型、PD型等迭代学习控制算法。为简化控制器的设计,本文采用P型迭代学习控制,从而迭代学习率为:

式中 f为学习增益。
迭代学习控制对系统周期性扰动具有抑制效果,但是对非周期扰动则无法抑制,并且随着迭代次数的增加非周期扰动将逐渐累积。为了削弱非周期扰动的累积效应,需引入松弛因子a,则得到迭代学习率:

由文献[12]知,迭代误差收敛的充要条件为a=1或∣a∣<1。
1.2 迭代学习控制对PMSM系统中周期性扰动的抑制能力分析
基于ILC的控制系统简图如图2所示:
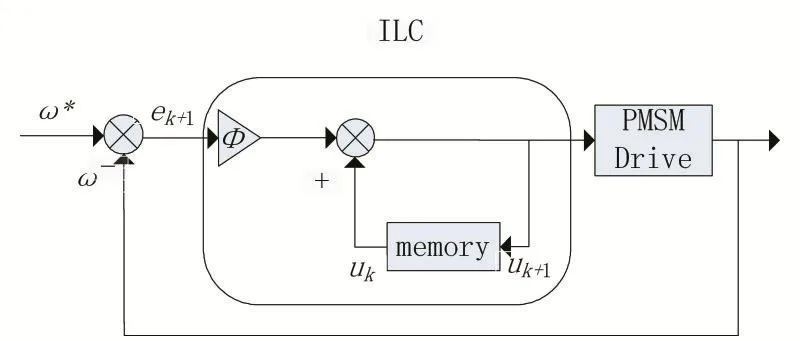
图2 迭代学习控制系统框图
PMSM采用转速、电流双闭环矢量控制,内环采用传统PI控制器,外环采用迭代学习控制器。由于内环时间常数远小于外环,假定电流实时跟踪给定值,即有Te=Te*=Keiq*,其中Ke为电机的转矩系数则电机模型可简化为输入为iq、输出为ωr的传递函数。当电机稳定运行时,存储器输入与输出时间间隔固定,可视为延时环节e-τs,其中τ即为延迟时间。故可将系统用传递函数形式表示,如图3所示:
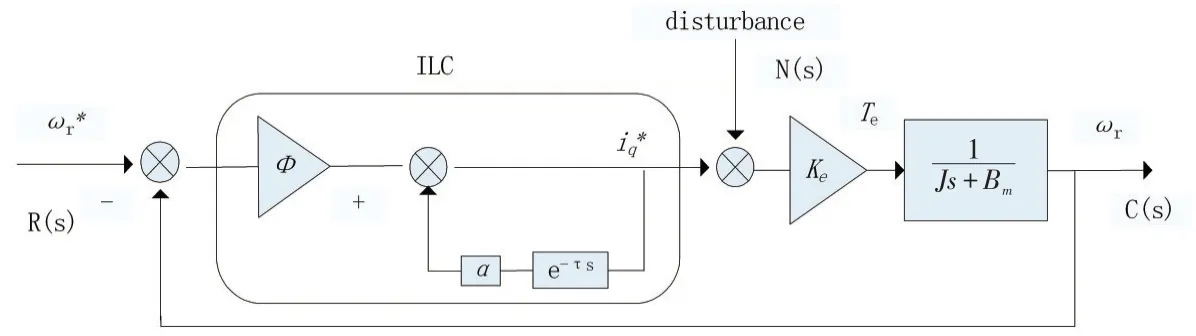
图3 ILC控制系统传递函数框图
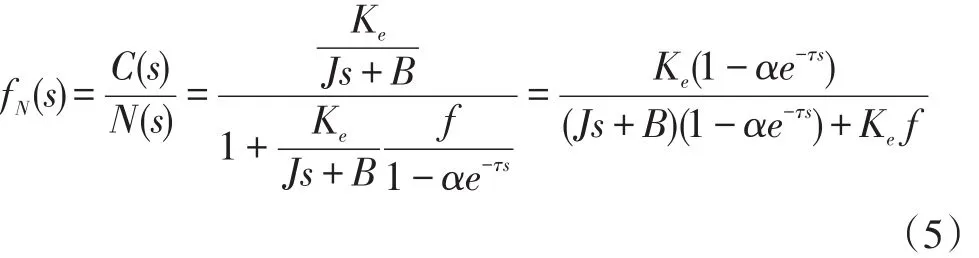
为了抑制周期性扰动,应满足存储器的延迟时间τ与扰动周期Tripple一致。取τ等于转矩波动一次谐波周期,即:

式中ωe=pωr为电机的电角速度。
从而有:

于是式(5)可简化为:
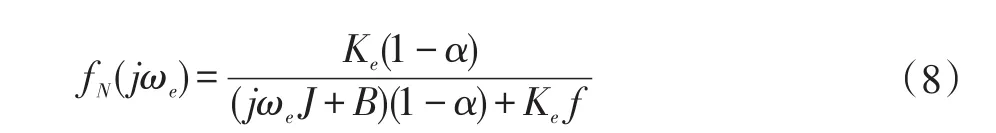
由式(8)可知,当a=1时等式为0,故可以完全抑制周期性扰动对系统输出产生的影响,且a越接近1,抑制作用越强。而a较大时,将造成非周期扰动的积累,严重时可能造成算法发散,因而通常将a取为小于1但尽量接近1的值。并且当a较大时,在动态过程中易造成系统较大波动。由此可见,a值的选取,对系统动静态性能有较大影响。为了选取合适的a值,本文基于误差最小原则对a值进行在线调节。
2 迭代学习控制参数在线调节

式中状态变量x(k)=ω(rk),输入u(k)=i(qk),输出y(k)=ω(k),w(k)为扰动量,
r,C=1,Ts为采样周期。
通常假定初始状态x(0)=0。当k分别取1,2,…,N时,得到N组等式,整理成矩阵形式即:

式中:
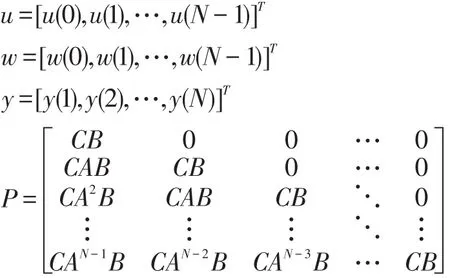
对于线性定常系统,P、Q均为常数矩阵。对第j次迭代及第j+1次迭代,式(11)可分别写成:

两式作差得:

系统输出误差为:

式中,y*=[yr(1),yr(2),…,yr(N)]T为系统期望输出。迭代学习率为:

将式(13)及(14)代入式(12),整理得:

为了选取合适的a值,需要构造一个最优问题并进行求解。仿照文献[12]可构造最优问题如下:
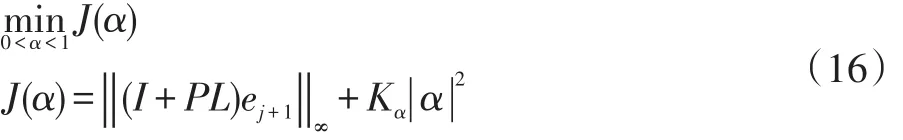
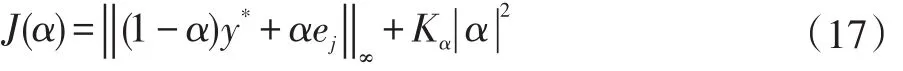
为求解最优a值,根据极值法将上式对a求导,并令导数为零,即解得a表达式:

若Ka取定值,可知a与‖ej‖∞成线性关系。在式(g)中可将 Ka视为|α|2项的权重。在动态过程中,即‖ej‖∞较大时,应重点考虑使 ‖ej‖∞减小,故 Ka应取较小值;而当‖ej‖∞较小时,则可以增大Ka取值。这样a与‖ej‖∞将不再成线性关系,其取值关系可以近似由图4表示:

图4
图4中曲线近似于sigmoid函数曲线的一部分,可将式(18)拟合为:

3 仿真结果及分析
为了验证方法的有效性,在MATLAB/Simulink环境下建立了PMSM矢量控制系统仿真模型。电机参数如表1所示。
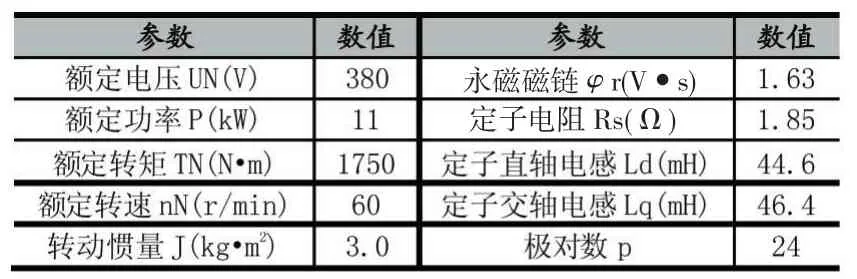
表1 PMSM仿真模型主要参数
在理想系统模型条件下,电机转矩响应中没有明显的周期性波动,为了验证算法的有效性,需要在仿真模型中加入扰动,使得转矩波形中含有谐波。因此在三相电流信号中加入0.2A的直流偏置误差及5%的增益误差。
图5给出了采用PI控制器和迭代学习控制器的仿真结果。仿真中,电机参考转速为30r/min,负载转矩为400N.m。转速环PI控制器参数为:Kp=2.02,Ki=47.65。电流环PI控制器参数:Kp=8.22,Ki=340。迭代学习控制器参数为:a=0.8,ϕ=2.02。仿真步长为Tstep=2μs。由图 5(a)与(b)可知,与 PI控制相比,采用 ILC时转矩与转速波动均得到明显抑制。则采用ILC后,转矩波动系数由7.25%下降到4.75%,转速波动系数由1.6%下降到0.38%。
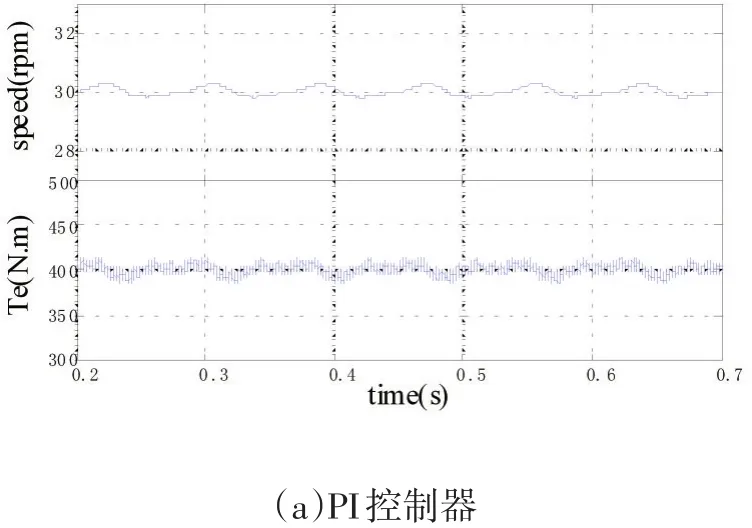
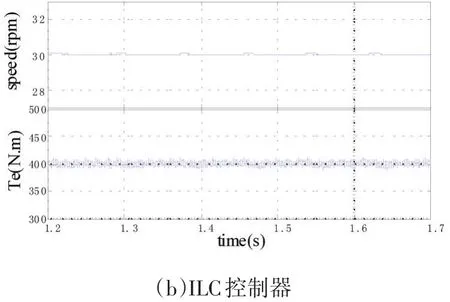
图5 30r/min时稳态响应波形
为了验证在不同转速下都能对转矩波动有效抑制,图6给出了15r/min时的仿真波形。由(a)与(b)比较可知,采用采用ILC后,转矩波动系数由5.25%下降到3.5%,转速波动系数由3.26%下降到0.73%。仿真结果表明,在不同转速,亦即不同波动频率下,转矩与转速波动均能得到有效抑制。

图6 15r/min时稳态响应波形
为了验证本文参数自适应型ILC在对系统动态过程的改善作用,图7和图8分别给出了在负载阶跃和转速给定阶跃过程中,分别采用α固定和α可调的ILC的动态响应仿真结果。固定的α值取为0.8。
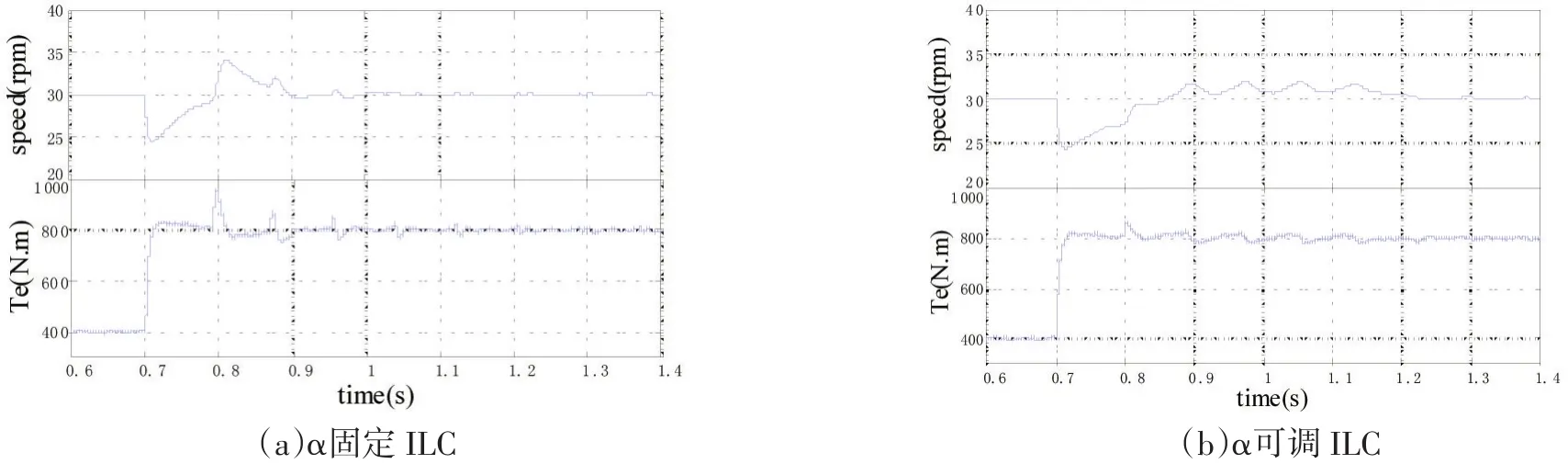
图7 负载阶跃动态响应波形

图8 转速阶跃动态响应波形
由图7与图8的仿真波形可知,与α值固定相比,可调型ILC的动态过程更加平稳。
4 结语
本文通过对永磁同步电机周期性转矩波动问题的研究,提出了基于参数自适应迭代学习控制的抑制策略,对迭代学习控制策略抑制周期性扰动的能力进行了分析,在抑制转矩波动的同时,加快了算法收敛速度,改善了系统的动态性能,仿真结果验证了本文算法的有效性。
