一种改进的结构化LRR算法

张燕

（上海海事大学信息工程学院，上海 201306）

0 引言

近年来，子空间分割在图像表示、计算机视觉和一些其他相关的领域起着非常重要的作用。所谓子空间分割，就是把数据样本划分到他们所属的类别中。在目前的研究中[1-11],[20]，常用的子空间分割方法有：代数法[1]、迭代法[2]、统计法[3]和基于谱聚类的方法[4-11]。其中，谱聚类的方法在实际的应用中取得了极大的成功。

一般来说，可以将基于谱聚类子空间分割算法分成两大步骤：1）通过所给的数据集，利用相关算法计算得到相似矩阵；2）根据得到相似矩阵，利用相关谱聚类算法得到分割结果（常用的分割算法有Ncut[12]）。根据现有研究可以发现，在子空间分割任务中，相似矩阵的好坏直接影响着最后的分割结果。

目前，对于如何获取相似矩阵的研究主要集中在自我表示模型上。自我表示模型的主要思想是指每个数据样本可以被来自同一类数据集中的其他样本线性表示。在此基础上，Elhamifar等人首次提出了稀疏子空间分割算法（SSC）[13],该算法通过最小化l1范数[14]来计算每个数据样本的系数矩阵，然后通过集中重构系数矩阵向量得到系数相似矩阵。SSC旨在获取每个数据样本的最稀疏表示，但是该算法却忽略了最终解的全局约束。为了解决有损数据的全局约束问题，Liu等人提出了低秩表示算法（LRR）[15]来获取所有样本的重构系数矩阵，该算法通过最小化矩阵的核范数[16]来实现系数矩阵的最小秩的要求。相关实验表明，最小核范数约束能够更好地发掘有损数据的全局结构。所以，在有损数据的子空间分割问题上，LRR的性能比SCC要好得多。

LRR在获取相似矩阵上取得的成功也促使很多学者也在此基础上做了很多相关的后续研究。例如，Chen等人[17]提出的用来获取高维数据集的子空间结构的对称低秩表示算法；Zhuang等人[18]提出的从非线性流形混合数据集中获取非直接的相似矩阵的局部低秩表示算法；Zhang等人[19]提出的通过一个有监督的学习方法创建一个判别重构字典的结构化低秩表示算法；Wei等人也相继提出了自我正则固定秩分割算法[20]和谱聚类指导低秩分割算法[21]。Zhuang等人[22]提出的一种将非负和稀疏约束结合应用在LRR算法中的非负低秩稀疏表示（NNLRSR）。相关的实验表明上述算法在不同的数据集的子空间分割应用中都能够获得不错的效果。

然而，传统的LRR算法仅适用于子空间完全独立的状态。我们知道，在实际应用中，子空间完全独立的是一种非常特殊的情况。因此，Tang等人[23]提出了结构化约束低秩表示算法（SCLRR）来改进LRR在不相交数据集中的应用，该算法通过在LRR的目标函数中加入一个正则项来获取数据集的结构信息。事实证明该方法对于多重不相交子空间分割是非常有效的。而且在SCLRR的基础上，Liu等人[24]提出了将低秩约束和结构信息相结合于系数矩阵的结构低秩字典学习算法；Wu等人[25]也提出了CS-LRR来获取最佳谱聚类；前面提到的Wei等人[21]提出的SCSLRR算法也可以看作是SCLRR算法的拓展。以上的算法都表明，SCLRR是一个切实有效并得到广泛认可的结构化LRR算法。

对于SCLRR，新引入的正则项带来了一个新的调节参数，并且该参数对算法的正确率有着直接的影响。但是我们知道，原始的LRR已经有了一个调节残差项的参数，因此，SCLRR算法变成了很难调节的双参数问题。而且在SCLRR基础上提出的其他算法[21],[24-25]也不可避免引入了新的参数。如图1所示。

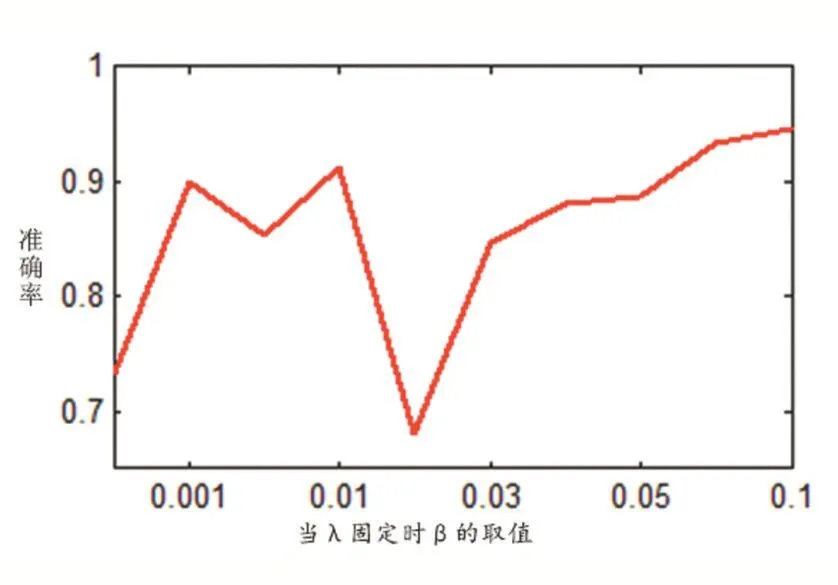
图1 当参数λ固定时算法SCLRR对参数β的敏感度

我们给出了在数据集Fashion-MINIST[29]上的一个简单测试来观察算法SCLRR对参数β的敏感度。我们可以发现，算法SCLRR的性能随着β的变化而发生很大的变化。因此，我们尝试去寻找一种新的方式来在LRR中引入数据集的结构化信息。在本文中，我们提出了一种改善的结构化低秩表示算法ISLRR。在ISLRR中，我们将数据集的结构化信息引入到LRR的等式约束的系数矩阵中，从而得到一个结构化的系数字典来计算获得结构化的低秩解。相关的实验表明，本文所提出的ISLRR在处理不相交数据集的子空间分割问题上简易有效。

1 相关算法介绍

在本节中，我们对算法LRR和SCLRR进行简要的介绍。

1.1 LRR算法

假设一组数据 X=[x1,x2,...,xn]∈Rd×n，其中 d 是每个数据样本的维度，n是所有数据样本的数量。由于每个样本能被来自相同子空间的其他样本线性表示，我们可以将自我表达模型定义如下：

其中，A = [a1,a2,…,am]∈Rd×m是字典，Z 是系数表示矩阵。在LRR中，我们将数据集X本身作为数据字典，则模型可以写为如下：

然而，在实际应用中，数据点一般都是充满噪声或是受损的。而且我们知道，核范数可以用来实现低秩约束，所以考虑到这些因素，可以将标函数改写如下：

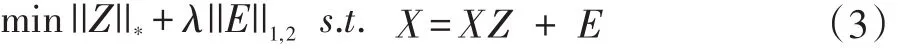
我们可以ALM算法来解决公式（3）的最优解问题。一旦求得了Z，定义G=[Z+ZT]/2作为相似矩阵并使用Ncut[12]算法获取最后的分割结果。

1.2 SCLRR算法

我们知道，LRR算法只能在子空间完全独立的情况下才能取得很好的效果。然而，独立子空间在不相交子空间问题中是一种特殊的情况。为了改善LRR在不相交子空间分割中的应用，SCLRR算法在LRR的目标函数中引入权值系数矩阵来改善其解的结构。通过这种方式，秩的惩罚项将会比只考虑核范数的情况要小的多，也就是说，该种方式能够很好地改善解的结构。考虑到噪声等情况，SCLRR的目标函数定义如下：

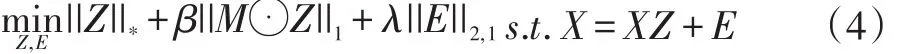
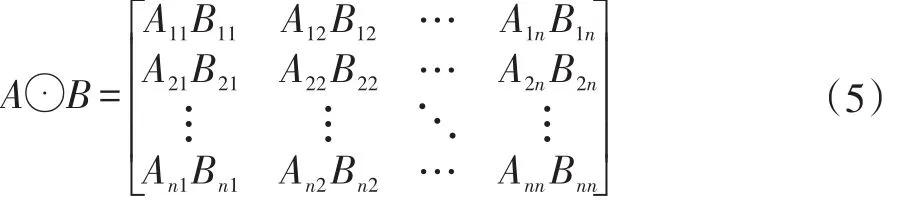
其中⊙叫作Hadamard积[22],β和λ是两个平衡参数。如果有两个相同大小m×n的矩阵，则Hadamard积表示如下：

相关的实验表明，SCLRR比LRR更能发掘不同数据集的子空间结构。

2 改良的结构化LRR算法

在本节中，我们提出了一种改良的结构化LRR算法并将其命名为ISLRR，并给出了算法的一般求解步骤。

2.1 算法提出动机

从文献[10]、[23]中我们得到，LRR得到的解的结构直接影响着最后的分割结果。根据LRR在独立子空间问题中的解的结构中发现，我们希望得到的块对角结构的解能够准确揭露类内数据样本之间较强的关系和类间数据样本之间较弱的关系。

并且我们知道，LRR在处理不相交子空间情况下的能力是比较弱的。为了改善LRR的相关性能，我们需要找到一种能够准确地将得到的解进行结构化的方法。而且在LRR算法中引入结构特征的目的也是希望能够获得一个能够用于不相交子空间问题中的块对角矩阵。从对SCLRR的介绍中，我们知道SCLRR算法比LRR更能准确地揭露不相交数据集的子空间结构，但是该算法却引入了额外的参数β来增加了算法的调节难度。

因此，我们希望能够有一个不引入新的参数但是却能准确获取到数据集的结构信息的方法。在LRR[7][8]中，我们知道系数矩阵Z用来表示数据集的内部结构。在SCLRR的描述中，权值矩阵M可以准确揭露数据样本之间的关系。我们假设能够在一组数据集X=[x1,x2,...,xn]∈Rd×n中获得权值矩阵 M ，那我们可以得到一个新的结构化系数矩阵M⊙Z来反映数据集的结构信息。不同于SCLRR的是，我们将该结构化的系数矩阵应用于LRR的等式约束项中，从而形成一个新的结构化公式来准确表示每个数据样本，并最终得到一个结构化的低秩解用于子空间分割。综上，考虑到噪声等原因，我们将ISLRR的目标函数表示如下：

很明显，当我们把M的所有元素设置为1时，我们可以将ISLRR转化为LRR。也就是说，我们可以将LRR考虑为ISLRR的一种特殊情况。当得到结构化的低秩解Z，我们定义G=(Z+ZT)/2坐为相似矩阵并用于最后的子空间分割。

一般来说，我们期望权值矩阵M的元素取值情况是类间样本的权值尽可能小而类内样本的权值尽可能大。根据文献[23]，本文也将权值矩阵M定义如下：

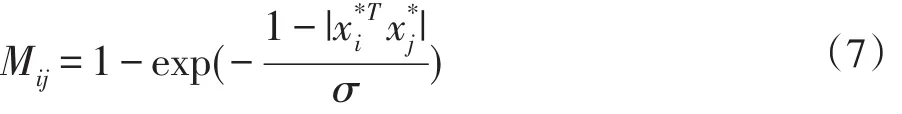
2.2 最优化相关解及算法步骤

为了获取问题（6）的最优化解，我们引入两个辅助参数J和T在目标函数中，并将公式（6）表示如下：

则公式（8）的增广拉格朗日函数可以表示如下：

其中Ya,Yb和Yc是拉格朗日乘子，μ＞0是一个参数。我们可以通过一个迭代算法来最优化以上未知项。

然后我们可以得到Z, J, T, E的每次更新如下：

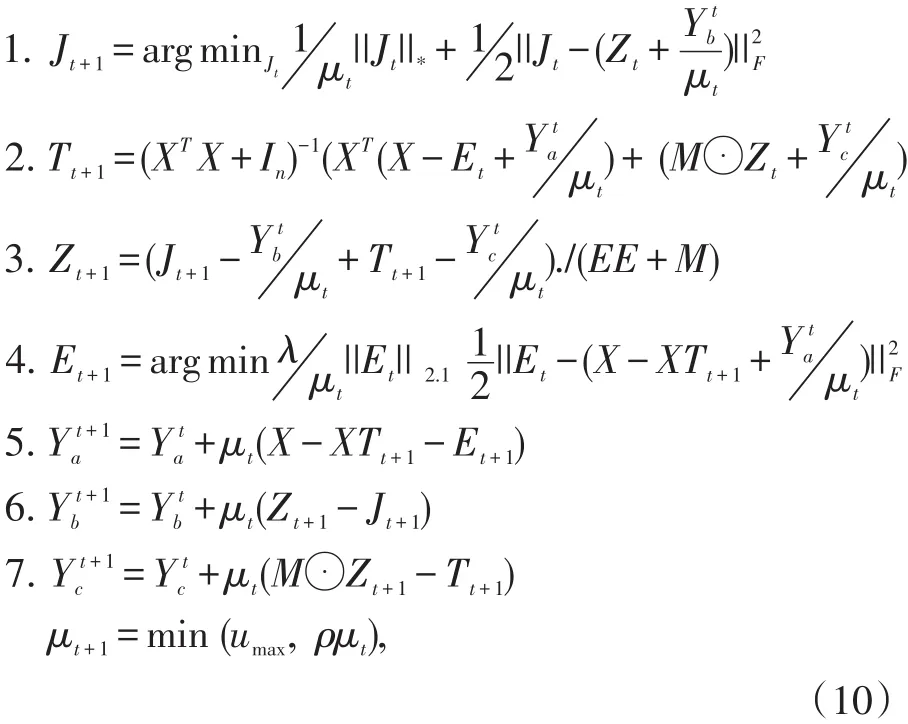
其中，μmax和ρ是两个调节参数，t是迭代次数。根据以上描述，算法ISLRR的基本步骤可以总结如下（通过计算得到低秩矩阵Z,得到相似矩阵G=(Z+ZT)/2,再通过Ncut切割算法得到最后的分割结果）：

算法1：ISLRR

输入：数据集X,参数λ,权值矩阵M,最大迭代次数Maxiter.

输出：系数矩阵T,低秩矩阵Z和噪声矩阵。

1.初始化参数：

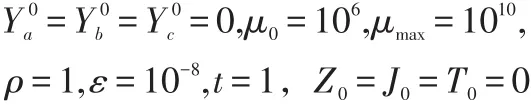
2.while||X-XT-E||∞＞ ε,||Z-J||∞＞ εand t＜Maxiter.执行

3.更新错误!不能通过编辑域代码创建对象。根据公式.(14)-1,2,3,4

5.t=t+1;

6.end while

7.return系数矩阵T=Tt,低秩矩阵Z=Zt,噪声矩阵E=Et

3 实验结果

为了验证ISLRR算法的可行性和算法效果，我们采取一些常用的人脸数据集：Extended Yale B[27]和AR[28]和图像数据集Fashion_MNIST[29]来验证我们的算法。并且，我们也选用几个经典的子空间分割算法SSC[4],LRR[7-8]和SCLRR[23]来进行对比试验。

本次实验的硬件配置是环境是Intel Core i5-6500 3.20GHz处理器，4GB运行内存，500G的硬盘内存。软件环境是64位Windows 7 Professional操作系统，MATLAB R2014a。

下面，我们将对实验中3个数据集进行简单的介绍：

Fashion-MNIST数据集是一个商品数据集，一共包含60000个训练样本和10000个测试样本。它们被分为十个大类，分别是：T恤、裤子、连衣裙、外套、衬衫、运动鞋、凉鞋、包和短靴。在本次实验中，我们选取训练集中每个类别的前50张照片作为实验数据集，每张照片的大小为20×20。Fashion-MNIST样本图片如图2（a）。

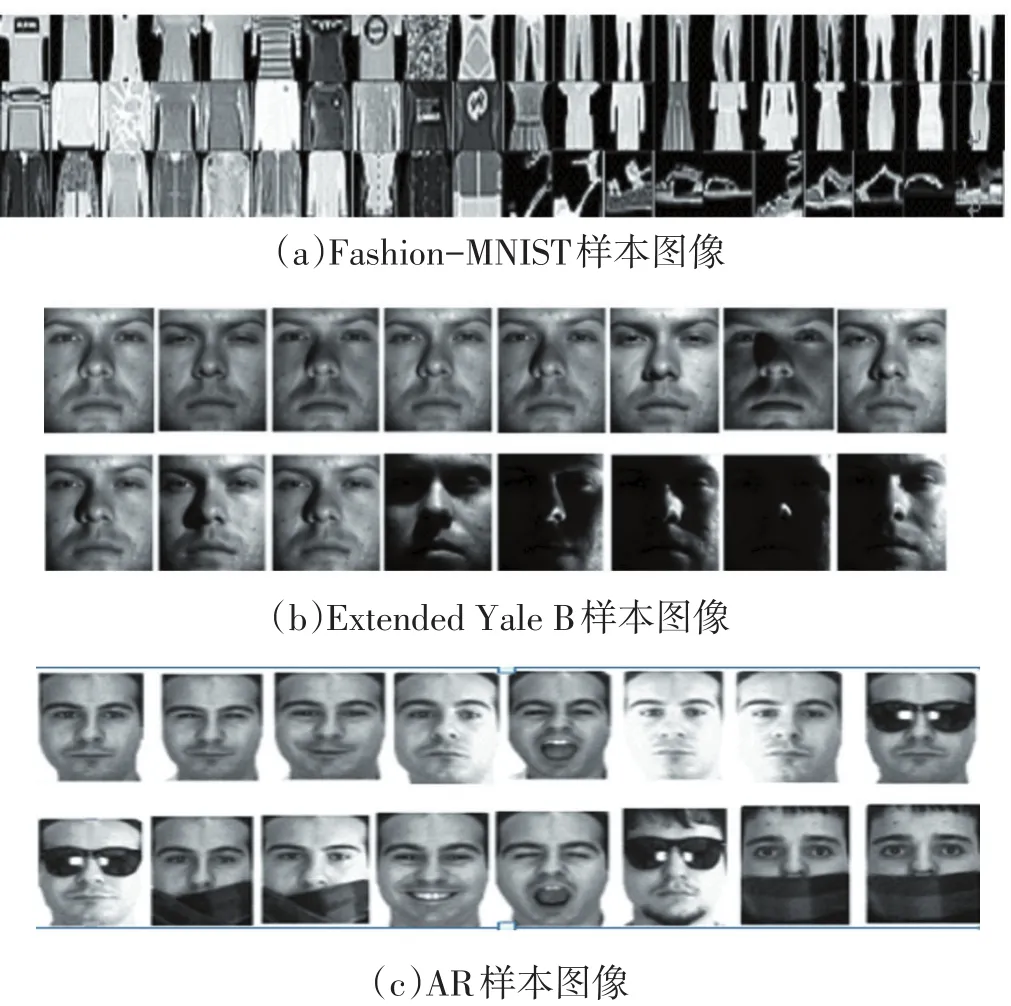
图2 静态图像样本

Extended Yale B人脸数据集包含38个不同的对象一共2414张图像，每个成员对象有9个不同的姿势，每个姿势有64个不同的灰度级。并且，这些图像还拥有不同命的光照环境和人脸表情。在本次实验中，我们将每张照片裁剪成32×32大小，样本图片见图2（b）。

AR人脸数据集拥有126个对象超过4000张的图片。每个对象拥有2模式26张图片，也就是说，每个模式又15张图片。这些图片都是在不同的视角和光照条件下拍摄而成的。在本次实验中，我们选取每个成员对象的前120张照片（一共2000张）作为实验数据集，我们将每张图片的大小裁剪为50×40。样本图片见图 2（c）。

图3 不同的算法在不同的数据集上随着分类数量变化准确率的变化和其他算法的对比

为了验证算法的有效性和可行性，本文将ISLRR算法与SSC、LRR和SCLRR几个经典的子空间分割算法进行对比试验。

我们针对每个数据集选取不同数量的类别进行实验。在实验中，我们选取q类（q的值选取范围为3～数据样本的类别总量）来计算相应的准确率。参数β的选取范围为[0.001,20]，参数λ的设置范围为[0.0001,50]，相应的最佳值如图3所示。

从图3可以看出：1）随着数据集类别数量的增加，所有算法的准确率都在下降；2）对于人脸数据集Extended Yale B，相对于其他几个算法，ISLRR算法在大部分情况下能够取得相对比较好的结果。

以上表明，ISLRR算法在一定的情况下用于的图像的子空间分割上能够取得不错的结果，也就是说，ISLRR在不相交子空间的分割应用中是一个有效的子空间分割算法。

4 结语

本文提出了一种新的子空间分割算法ISLRR，在ISLRR中，我们将数据集的结构信息引入到LRR的等式约束项中来改善解得的结构。对比SCLRR算法，ISLRR避免了带来新的参数，也就是说，该算法解决了SCLRR中调节双参数的困难。为了证实算法的有效性，我们用了三个相关的算法在四个常用的图像数据库上进行对比实验。最后的实验结果表明，ISLRR算法在解决不相交的子空间分割问题是简单可行的。