小麦籽粒振动筛分黏弹塑性接触模型构建及其参数标定

刘凡一，张 舰，陈 军

（西北农林科技大学机械与电子工程学院，杨凌 712100）

0 引 言

离散元法能够实时地通过颗粒-颗粒/几何体间的接触来计算颗粒受力和运动，因此其在农业物料振动筛分中得到了广泛应用[1-3]。颗粒接触模型是离散元法的重要基础，其准确性直接决定了颗粒所受力和力矩的大小，直接影响计算结果的准确性。

离散元接触模型主要包括两类：黏弹性接触模型和滞回接触模型。其中根据颗粒加载过程中的力-位移关系，黏弹性接触模型又可分为线性黏弹性和非线性黏弹性接触模型。1979年，Cundall和Strack最早提出linear spring模型[4]，该模型具有计算量小，计算时步大的优点。然而，linear spring模型采用线性弹簧和阻尼，其力-位移关系是完全线性的，这与大多数生物质材料非线性特性不符；此外，该模型在计算法向弹簧刚度时，需要指定颗粒特征速度，这增加了模型的使用难度。为解决力-位移关系完全线性的问题，学者们根据Hertz非线性接触理论先后提出了多种非线性黏弹性接触模型，其中常用的包括：Hertz-Mindlin(no slip)模型[5]、Kuwabara and Kono 模型[6]。

为模拟颗粒材料的塑性变形，Walton等[7-11]先后提出了多种滞回接触模型。根据力-位移关系的不同，滞回接触模型可分为线性滞回模型和非线性滞回模型。滞回接触模型都有一个共同的特点，即加载和卸载阶段弹簧刚度不同，以此表征接触过程中的塑性变形及能量损失。

关于现有接触模型在农业物料颗粒动力学模拟中的计算精度，Wojtkowski等[12]通过不同含水率的油菜-钢板碰撞研究了黏弹性接触模型和滞回接触模型的计算精度，结果表明：对于低含水率的颗粒，滞回接触模型计算精度高于黏弹性接触模型；但对于高含水率的颗粒，结果相反。Johnstone在应用Hertz-Mindlin(no slip)模型模拟谷物颗粒固结试验时发现：由于该接触模型缺少塑性，导致卸载过程中发生过量的弹性回弹，同时这也使得再加载-卸载过程中不再有形变发生[13]。与大部分工业生产中的颗粒材料不同，农业固体物料流变学特性研究表明农业物料颗粒往往同时具有 3种基本性质：弹性、黏性以及塑性[14]。现阶段，有关黏弹塑性材料接触理论已进行了大量研究[15-17]，但对农业物料黏弹塑性接触模型的研究还较少。卢立新等[18]基于果实等速压缩变形特征,提出了由3个非线性弹簧元件、1个黏性元件以及1个滑块元件组成的黏弹塑性模型，并通过试验对所建立的模型进行了验证。郑晓等[19-20]在物料流变学试验基础上，采用理论模型与经验模型结合的方法，先后建立了油菜籽、芝麻及花生的非线性黏弹塑性本构模型。

为更好地模拟麦粒振动筛分过程，本研究在现有离散元接触模型基础上，构建了一种黏弹塑性接触模型，并结合真实试验（加载-卸载、碰撞及旋转鼓）对其参数进行标定，最后通过振动筛分试验对标定结果进行验证。

1 黏弹塑性接触模型构建

该黏弹塑性接触模型通过 EDEM 2.7软件应用程序编程接口（application programming interface, API）实现，该接口允许用户通过C++语言构建用户自定义接触模型、自定义颗粒工厂以及自定义耦合接口。

法向方向，该接触模型通过将Kuwabara and Kono非线性黏弹性接触模型中的黏性耗散项引入Thornton滞回接触模型[9]进行构建。与 Thornton接触模型相似，该接触模型法向分量包括4个阶段。

第一阶段为黏弹性加载/卸载阶段，该阶段颗粒接触重叠量小于屈服重叠量δy，其法向接触力Fn计算式为

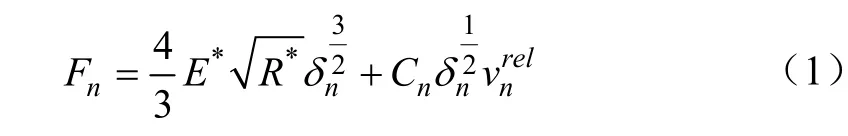
其中

式中E*为等效弹性模量，Pa；R*为等效接触半径，m；δn为颗粒-颗粒/几何体法向接触重叠量，m；Cn为颗粒-颗粒/几何体法向阻尼系数；为颗粒-颗粒/几何体法向相对速度，m/s；Ei、Ej为颗粒/几何体的弹性模量（i、j均为颗粒/几何体编号），Pa；νi、νj为颗粒/几何体的泊松比；Ri、Rj为颗粒/几何体的接触半径，m。

第二阶段为黏塑性加载阶段，其法向接触力Fn计算式为

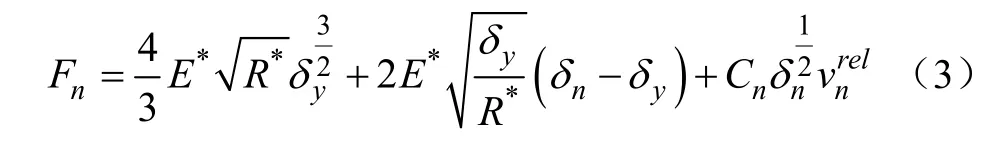
第三阶段为黏弹性卸载/重加载阶段，其法向接触力Fn计算式为

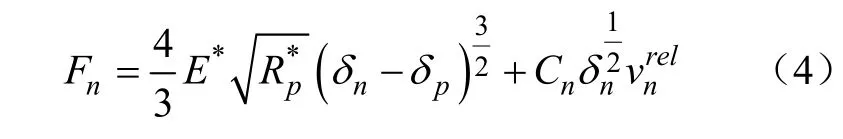
式中Fnmax为最大法向接触力，N；Fny为屈服力，其值等于颗粒发生屈服时的法向接触力，N；δnmax为最大法向接触重叠量，m。

第四阶段为颗粒塑性变形恢复阶段，颗粒间法向接触力Fn始终为0，直至颗粒发生完全分离。

切向方向采用简化Thornton切向接触模型[21]。该接触模型基于Mindlin and Deresiewicz非滑移接触理论，计算切向力时在每一时步中对上一时步切向力进行修正，第n时步切向接触力计算式如式（6）～（8）所示。如果 Ft≤μFn，则

式中ΔFn为法向接触力增量，N；kt为切向弹簧刚度，N/m；Δδt为切向重叠量增量，m；a为接触面半径，m；G*为等效剪切模量，Pa；Gi、Gj为颗粒/几何体的剪切模量，Pa。

如果 Ft＞μFn，则

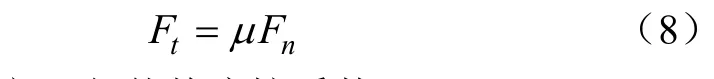
式中μ为颗粒-颗粒/几何体静摩擦系数。

滚动摩擦力矩计算同 Hertz-Mindlin(no slip)接触模型，通过接触面上的力矩Ti计算得到，即

式中μr为颗粒-颗粒/几何体滚动摩擦系数；ωi为接触点处颗粒的单位角速度矢量，rad/s。

2 模型参数标定

标定试验中所用麦粒由西北农林科技大学小麦育种中心提供，品种号为西农 223，含水率为 10.05%，密度为1 350.30 kg/m3。麦粒为三轴不等颗粒，随机选取150颗利用数显游标卡尺（精度：0.01 mm）对其三轴尺寸进行测量，得到平均长、宽、厚分别为6.21、3.16和2.93 mm。麦粒弹性模量通过 ASAE S368.4[22]标准测量得到，其值为1.93×109Pa，泊松比取0.40[23-25]。研究中几何体材料为钢，其密度、剪切模量和泊松比分别为7 800 kg/m3、7×1010Pa和 0.30。

大量研究表明，精确的颗粒模型并不能显著提高模拟精度，通常只需通过少量的单元球建立粗略的非球形模型即可得到较好的模拟精度[26-28]。因此，根据麦粒三轴尺寸，采用如图4所示的19球填充颗粒模型（长×宽×厚：6.21 mm×3.16 mm×2.93 mm）。在旋转鼓及振动筛分模拟中，基于真实麦粒长轴尺寸分布，确定仿真中麦粒按照标准正态分布生成（平均值为1，标准差为0.06）；为避免生成过小及过大的颗粒，根据实际测量得到的最小、最大颗粒尺寸，将颗粒半径限制在 0.65～1.21倍的初始半径之间。在所有模拟中，仿真时步取1×10-7s，网格尺寸取最小球形单元半径的3倍。

据上述黏弹塑性接触模型中法向接触力计算公式，可知待确定参数包括麦粒屈服重叠量 δy以及麦粒-麦粒/钢板法向阻尼系数Cn。单轴加载-卸载试验中，加载板速率较小，整个过程可看作是准静态的，可以忽略法向阻尼系数Cn的影响（模拟中阻尼系数为0），因此采用单轴加载-卸载试验即可对麦粒屈服重叠量δy进行标定。恢复系数反应了物体碰撞过程中的能量损耗，故选用碰撞试验中所测恢复系数去标定麦粒-麦粒/钢板法向阻尼系数。

对于切向接触力和滚动摩擦力矩，待确定参数包括麦粒-麦粒/钢板静摩擦系数及滚动摩擦系数。颗粒材料在旋转鼓试验中的动态休止角能够很好地反映颗粒的流动特性，常被用于颗粒离散元参数的标定[13]，此外麦粒在振动筛分过程中是动态的，因此选用旋转鼓试验对其摩擦系数进行标定。预试验结果表明，对于本文中所建立的模型，滚动摩擦系数对动态休止角影响较小，因此本文中麦粒-麦粒/钢板滚动摩擦系数均取 0.05，只对麦粒-麦粒/钢板静摩擦系数进行标定。

2.1 单轴加载-卸载试验

随机选取10颗麦粒，采用DDL10型电子万能试验机（长春机械科学研究院有限公司，长春）进行单轴加载-卸载试验（加载速度为1 mm/min），得到麦粒平均力-位移曲线如图1所示。由力-位移曲线可以看出，即使在位移量较小的情况下（0.10 mm），麦粒仍然表现出显著的塑性行为。

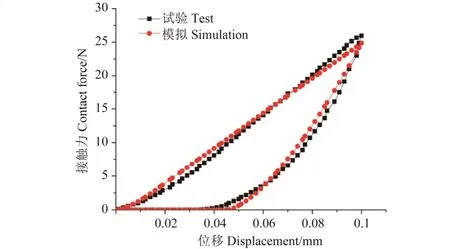
图1 麦粒单轴加载-卸载试验中力-位移曲线Fig. 1 Force-displacement curves in uniaxial loading-unloading test of wheat

利用EDEM软件模拟麦粒单轴加载-卸载试验，得到各采样点处模拟-试验接触力误差平方和D随屈服重叠量δy的变化规律如图2所示。通过Origin 8.0软件拟合，发现二者关系可以通过方程（10）表示。

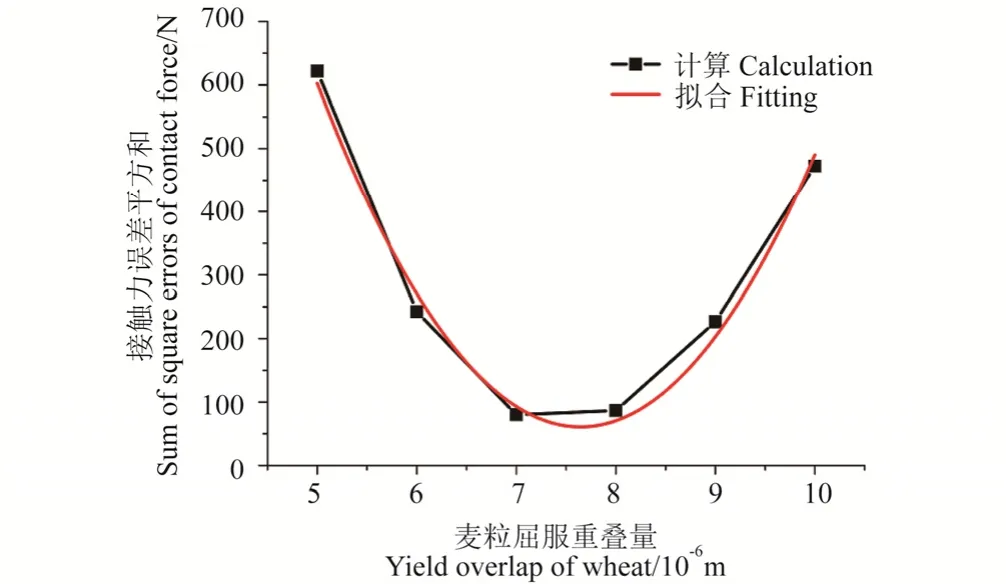
图2 接触力误差平方和随麦粒屈服重叠量变化趋势Fig. 2 Changes of sum of squared errors of contact force with yield overlap of wheat

求解方程(10)可得，当麦粒屈服重叠量为7.63×10-6m时，模拟-试验接触力误差平方和最小（D=60.83 N），此时模拟所得麦粒力-位移曲线如图1所示，从中可以看出模拟值与真实试验值非常接近，说明麦粒屈服重叠量标定结果良好。

2.2 碰撞试验

2.2.1 麦粒-麦粒

麦粒-麦粒恢复系数采用 Gonzálezmontellano等[29]所用双摆装置进行测量，测量原理如图3。测量时，为防止释放时麦粒具有一定的初速度，颗粒 1由真空泵吸引，静止在高度为h0处。关闭真空泵，颗粒1在重力作用下开始向左摆动，至最低点处（高度为0）与颗粒2发生碰撞。碰撞后，颗粒1、2均向左摆动，摆动高度分别为h1和h2，麦粒-麦粒恢复系数epp可通过式（11）计算。

整个测量过程通过奥林巴斯I-speed3高速摄影机（奥林巴斯（中国）有限公司，广州）以500 fps记录。测量时，选取5组（10颗）麦粒，每组试验重复20次，得到麦粒-麦粒恢复系数为0.46±0.09。

图3 麦粒-麦粒双摆碰撞示意图Fig. 3 of double pendulum test of wheat-wheat collision

离散元模拟中，通过EDEM软件自定义颗粒工厂接口（API），将麦粒-麦粒双摆碰撞简化为无重力水平碰撞。如图4所示，碰撞前，颗粒1、2水平速度分别为v1、v2；碰撞后，两颗粒的速度分别为v3、v4。根据恢复系数的定义，麦粒-麦粒恢复系数epp计算如式（12）所示。

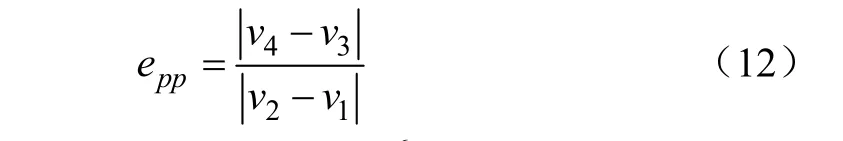
当麦粒屈服重叠量为7.63×10-6m时，改变麦粒-麦粒法向阻尼系数Cn-pp进行碰撞模拟，得到麦粒-麦粒恢复系数随法向阻尼系数变化趋势如图5a所示。利用Origin软件进行拟合，得到二者关系如下

以麦粒-麦粒恢复系数真实测量结果为目标值，求解二次方程可得麦粒-麦粒法向阻尼系数Cn-pp为190.68，此时模拟所得麦粒-麦粒恢复系数（0.44）与真实试验值的相对误差为4.35%。

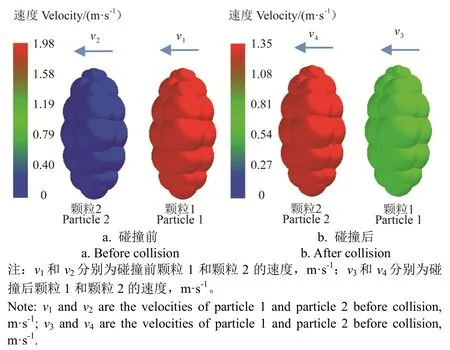
图4 麦粒-麦粒双摆试验离散元模拟Fig. 4 DEM simulation of wheat-wheat double pendulum test

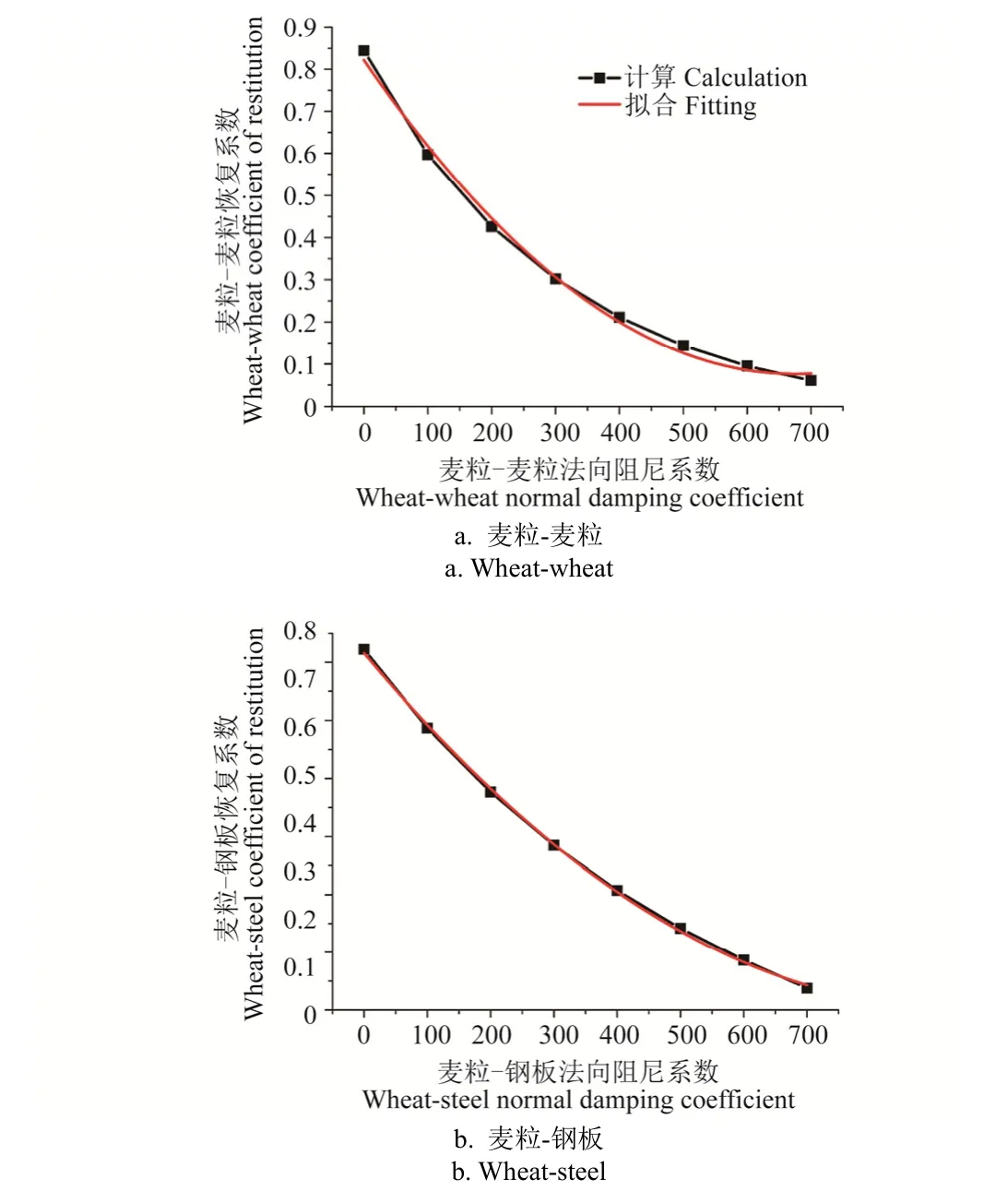
图5 恢复系数随法向阻尼系数变化趋势Fig. 5 Changes of coefficient of restitution with normal damping coefficient

2.2.2 麦粒-钢板

麦粒-钢板恢复系数采用类似黄小毛等[30]所用倾斜平面法进行测量，测量原理如图6a所示。测量时，同样采用真空泵通过吸头将麦粒吸住，此时麦粒相对碰撞点 O的高度为H0。关闭真空泵，麦粒与倾斜板发生碰撞后落在落料板上，落料板与碰撞点O的相对高度为H1，麦粒水平位移为S1；改变落料板与碰撞点O的相对高度（H2），得到麦粒水平位移为 S2，此时麦粒与倾斜板间的恢复系数epw可通过式（14）计算。

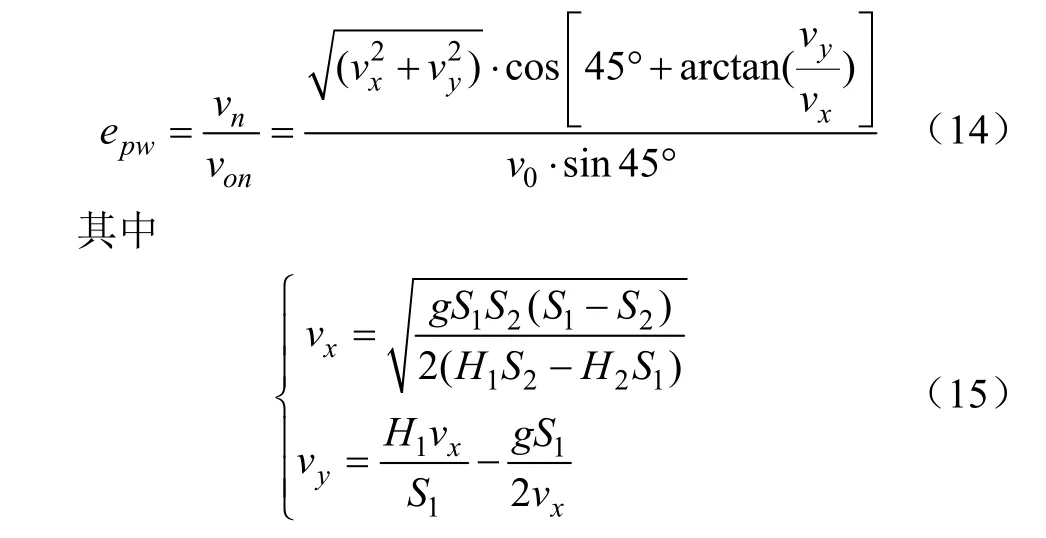
式中von、vn分别为碰撞前、后法向速度分量，m/s；vx、vy分别为碰撞后水平、垂直速度分量，m/s；v0为碰撞前垂直速度分量，m/s。

图6 麦粒-倾斜面碰撞试验Fig. 6 Wheat-inclined plane collision test

为防止麦粒与落料板接触后发生回弹，在落料板上涂上一层黄油以“捕获”麦粒。同时，麦粒与倾斜板碰撞后极易产生旋转，导致被测物同时具有X和Y方向位移，这与恢复系数计算时颗粒只具有 X方向的位移假设不符。因此，为减小麦粒 Y方向位移导致的测量误差，黄油在Y方向上的宽度为50 mm，即麦粒Y向位移小于25 mm时，麦粒将被落料板“捕获”，如图6b所示。测量时，随机选取50颗麦粒进行测量，得到麦粒-钢板恢复系数为0.48。通过EDEM软件模拟颗粒-倾斜面碰撞过程，改变麦粒-钢板法向阻尼系数Cn-pw，求得不同法向阻尼系数下的麦粒-钢板恢复系数，如图5b所示。拟合发现二者关系可以通过二次多项式进行表示。

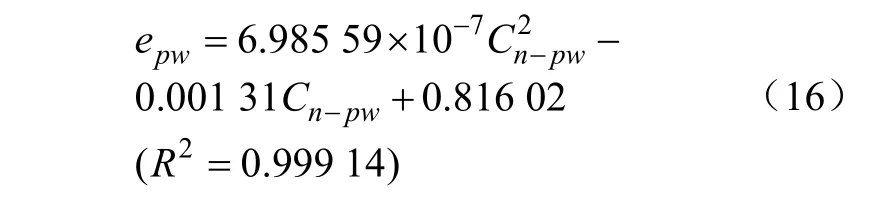
以麦粒-钢板恢复系数真实测量结果为目标值，求解所建立二次方程可得麦粒-钢板法向阻尼系数为306.65。采用标定参数模拟麦粒-倾斜面碰撞，得到恢复系数模拟值（0.479 02）与真实测量值（0.484 35）差距极小。

2.3 旋转鼓试验

旋转鼓试验设置与Johnstone研究中的设置相似[13]。其中，钢质旋转鼓内径和厚度分别为150和30 mm，为观察记录旋转鼓内颗粒流动，旋转鼓一侧采用有机玻璃挡板，如图7a所示。为获得平整的颗粒自由流动表面，旋转鼓的转速设为7 r/min，颗粒填充率为40%。麦粒在旋转鼓中的流动图像通过数码相机获取（快门1/1 600 s），随机选取5张图片进行动态休止角测量。

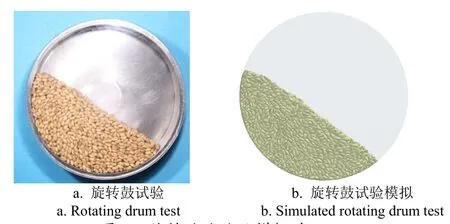
图7 旋转鼓试验及模拟对比Fig.7 Comparison of rotating drum in lab test and simulation

为减小人为因素导致的测量误差，采用计算机图像技术进行动态休止角测量。测量时，首先采用Image J软件截取圆形旋转鼓图像；然后在MATLAB中采用K均值聚类的方法提取图像边界点；最后通过线性拟合得到拟合边界，该直线斜率的反正切值即为麦粒动态休止角，本研究中测得麦粒动态休止角为（33.87±0.40）°。

动态旋转鼓模拟试验设置与真实试验一致，仿真总时间为5 s，从4.2 s开始，每隔0.2 s截取颗粒流动图像。结合国内外离散元模拟中麦粒-麦粒/钢静摩擦系数的取值[13,25,31-33]，确定了参数变化范围，具体参数组合及模拟结果如表1所示。从表1中可知，当麦粒-麦粒/钢板静摩擦系数分别为 0.40和 0.44时，旋转鼓动态休止角为（34.79±0.37）°，最接近真实试验值（如图7b所示）。

表1 旋转鼓模拟试验设计及其结果Table 1 Design and results of rotating drum simulation test

3 试验验证

为验证所建立的接触模型及标定的模型参数能否用于麦粒振动筛分试验，选用鱼鳞筛进行筛分试验，如图8所示。振动筛分试验中，鱼鳞筛开角、筛面倾角及振动方向角分别为15°、2°和15°，振幅为30.71 mm，频率为4 Hz。研究中筛分试验重复3次，每次试验中麦粒总质量为3.90 kg。模拟中考虑到筛面在宽度方向的完全对称及计算量[3]，宽度方向采用周期性边界条件选取100 mm进行建模，仿真中共生成31 706颗麦粒。

图8 振动筛分试验及其离散元模拟Fig.8 Vibratory screening test and its DEM simulation

为比较振动筛分试验及其离散元模拟结果，在筛面下方设置接料盒，并在长度方向将其分为 7个区间。待筛分完成后，统计试验及模拟所得各区间内颗粒质量分数，结果如图9所示。由图9可知，试验及模拟结果具有极为相似的变化趋势，筛下物分布均主要存在于前 3个区间，最大误差出现在第 2区间（8.97%）。为评价试验与模拟结果有无显著性差异，采用SPSS软件对2组数据进行配对T检验，得到其P值为0.99，远大于0.05，说明2组数据无显著性差异的概率为99%。同时，2组数据的相关系数为0.98，说明两组数据具有极高的相关性。综合分析，两组数据无显著性差异且高度相关，这表明所建立的黏弹塑性接触模型及标定的参数能够很好地模拟麦粒振动筛分过程。

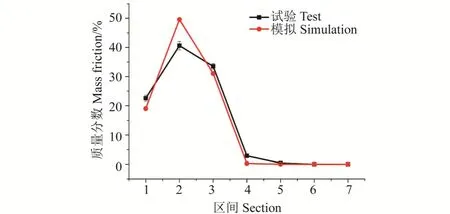
图9 振动筛分试验及模拟中筛下物分布对比Fig.9 Comparison of distribution of wheat in vibratory screening test and its simulation

4 结 论

本文以麦粒为研究对象，在现有离散元接触模型基础上，建立了一种黏弹塑性接触模型。利用单轴加载-卸载试验、碰撞试验及旋转鼓试验对麦粒接触模型参数进行标定，得到麦粒屈服重叠量为7.63×10-6m、麦粒-麦粒/钢板法向阻尼系数分别为 190.68和 306.65、麦粒-麦粒/钢板静摩擦系数的最佳组合为0.40和0.44。麦粒振动筛分验证试验表明所建立的接触模型及标定的模型参数能够很好地模拟麦粒振动筛分过程，模拟与试验所得筛下麦粒质量分数最大误差为8.97%。研究结果可为其他农业物料黏弹塑性模型构建及其参数标定提供参考。