山羊蹄底部非规则曲面仿生形貌数学模型构建及验证

2018-08-21王亚飞马田乐王甲甲徐锐良郭志军

农业工程学报 2018年15期

张伏，王亚飞，马田乐，王甲甲，徐锐良，郭志军

（1.河南科技大学农业装备工程学院，洛阳 471003；2.机械装备先进制造河南省协同创新中心，洛阳 471003；3.河南科技大学车辆与交通工程学院，洛阳 471003）

0 引言

随着农业自动化发展，农业机器人的研究得到众多学者的重视[1-6]。目前应用于农业的可移动机器人主要有履带式、轮式和足式[7]，履带式机器人通过性强但灵活差[8]，轮式机器人移动快但越障能力差[9]，足式机器人具有良好的越障能力和运动灵活性[10]。用于农业的足式机器人有四足机器人、六足机器人和八足机器人，因六足、八足机器人相对于四足机器人具有较多冗余性[11-12]，目前用于农业的足式机器人中四足机器人较多，但在农业作业时，由于农业地面环境复杂，对四足机器人的行走稳定性要求高，而四足机器人的足端形状是影响其稳定行走的关键因素之一[13-14]。四足机器人的足有平底形脚掌、圆柱形脚掌、球形脚掌、仿生脚掌；平底形脚掌、圆柱形脚掌、球形脚掌作为足式机器人足端结构，存在防滑性差，不能适应复杂地形的情况，而仿生脚掌以自然界动物脚掌为仿生原型，相对于其他形状的脚掌而言，具有对地面环境适应性强、行走阻碍小、越障性能好的特点[15-16]。在仿生足研究领域，相关学者做了大量研究，并取得丰硕的成果。吉林大学的佟金等[17]以黄牛为研究对象，分析黄牛在水稻田行走步态和牛蹄与土壤的作用力。西南科技大学的蔡楷旋[18]以黄牛为仿生对象，研究仿牛四足机器人，并对仿牛脚掌与地面接触进行仿真，仿牛脚掌比半球形脚掌机器人行走阻碍小。吉林大学的张锐等[19-20]以鸵鸟为仿生对象，研究鸵鸟足底非规则曲面形貌用于仿生巡视器车轮，得出仿生轮的牵引力提高。吉林大学的王骥月等[21-22]以山羊为仿生对象，研究山羊蹄匣用于仿生减震设计，仿生减振缓冲足受到冲击力的峰值小于普通减振缓冲足。本文从自然界获取灵感，以山地动物——山羊为仿生原型，结合工程仿生学技术，研究山羊在复杂地形稳定行走机理，有助于解决农业四足机器人在复杂地形行走稳定性差、越障能力差的问题。

山羊作为一种典型的山地动物，在崎岖地形的行走能力令人瞩目，且体型适中，四肢强劲有力；可自主选择最佳落足点，进行跨越运动；行走步态敏捷轻快，适于长距离运动[23-25]。此外，山羊经常在凹凸不平的地面上行走，四肢蹄掌表面进化出能适应不同地表的几何形状，且蹄掌附着能力较强[26-28]。山羊蹄底部特征形貌是其在复杂地形环境稳定行走的关键因素之一，研究山羊蹄底部形貌并结合仿生学原理设计仿生足，可改善农业四足机器人的行走稳定性和越障性能。因此，本文以山羊足为仿生原型，研究一种在复杂地形行走时适应性强、越障性能好的仿生足并将其应用于农业四足行走机器人，对解决农业四足机器人在崎岖地形难以稳定行走的问题具有重要意义[29-31]。

本研究基于逆向工程技术，获取山羊蹄底部非规则曲面三维点云数据，利用Matlab软件采用数据拟合的方法对山羊蹄底部曲面进行数学建模。

1 山羊蹄底部非规则曲面模型重构

1.1 山羊蹄底部曲面几何模型

为获取山羊蹄底部曲面几何模型，选取 6个月的雄性波尔山羊蹄，为便于扫描，在山羊蹄底部喷FA-5反差增强剂并粘贴哑光黑圆点标记点，如图1a所示。为得到山羊蹄的三维点云数据，将试验所用的山羊蹄放在自动转台上，采用天津微深科技有限公司的 VTOP系列三维扫描仪（如图1b所示）对山羊蹄进行扫描。

图1 试验材料与设备Fig. 1 Experimental materials and equipment

扫描得到的山羊三维点云数据如图2a所示。由于三维扫描仪扫描时会扫到山羊蹄周围的物体，因此得出的模型有噪声点和体外孤点。此外，由于山羊蹄表面凹凸不平，部分区域三维扫描仪较难扫描，出现漏洞等缺陷，须借助逆向工程软件 Geomagic Studio 对模型进行修复工作才能得出理想的山羊蹄几何模型。把三维扫描仪扫描得到的山羊蹄三维点云模型保存为.ASC文件，然后导入到Geomagic Studio软件中，利用Geomagic Studio软件中的删除噪声点、体外孤点功能删去模型周边的杂点。通过封装，把点云数据转化为由三角形组成的曲面模型，利用软件中的网格医生自动诊断功能自动识别山羊蹄模型需要修复的区域，并逐个对各个区域进行补漏洞、去除尖点操作，用去除特征、松弛网格、填充孔、锐化等命令对模型处理，处理结果如图2b所示。把点云数据多边形处理结果切换到精确曲面，进行创建曲面、栅格处理等一系列操作直至获取完整模型，模型如图2c所示。

图2 山羊蹄几何模型处理Fig. 2 Geometric modeling of goat’s hoof

对模型进行偏差分析，分析结果如图3所示，3D偏差的最大值范围为-6.098 9～+6.099 6 mm，平均值为-0.856 6～+0.678 3 mm，标准偏差为1.402 2 mm。

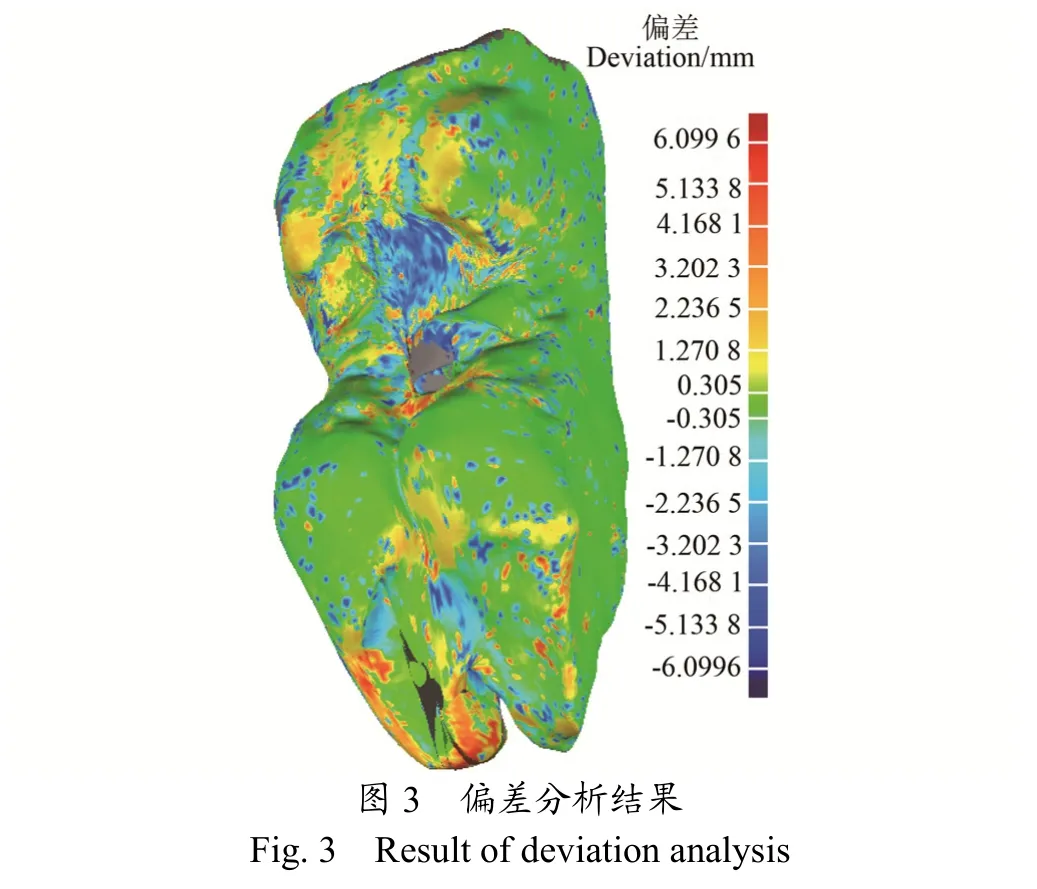
由图3可知，山羊蹄底部模型的偏差主要集中在-0.305 0～+0.305 0 mm之间，部分偏差范围为+0.305 0～+1.270 8 mm和-0.305 0～-1.270 8 mm，以及少数偏差范围为+1.270 8～+2.236 5 mm；在仿生设计时主要对山羊蹄底部非规则曲面进行设计，而模型底部的偏差相对于试验所用的山羊蹄底部长5.3 cm、宽3.8 cm和厚2.8 cm而言，满足工程设计上的允许误差范围±5%[32]，因此，山羊蹄几何模型处理结果满足工程仿生设计需求。

山羊蹄为偶形蹄，蹄底部为非规则曲面，据此，在Geomagic Studio 软件中对蹄底部分别处理，分为左侧和右侧。利用Geomagic Studio软件中的曲线切割功能对山羊蹄实现分割，获取的2个曲面如图4所示。

从分离出的 2个曲面形状发现，从山羊蹄底部上侧看，山羊蹄底部左侧部分呈现中间向上凸起，两侧向下凹陷，在蹄尖和蹄跟处凸起，山羊蹄底部右侧部分呈现中间凸起，往两端逐渐下凹。以上山羊蹄底部曲面形状是其长期在凹凸不平的地面上行走，进化出能适应不同地表的几何形状，此种蹄底部非规则曲面是山羊在崎岖地面稳定行走的关键因素之一。

图4 山羊蹄底部非规则曲面模型Fig.4 Irregular surface model of goat’s hoof

1.2 山羊蹄底部曲面点云处理

在Geomagic Studio软件中把2个分割好的由三角形组成的曲面转化为点云模型，并分别保存为.igs格式文件。把2个曲面的点云数据导入到Catia软件的数字化设计（Digitized Shape Editor）模块中，对曲面点云进行过滤处理。由于点云的数据量会影响后续曲面拟合的运算速度，且保留能体现山羊蹄底部曲面形貌的特征点，并以.txt文件格式导出2个曲面的特征点云三维坐标。

对 2个曲面分别进行非均匀过滤处理，过滤前后点云如图5所示，其中图5a和5b为过滤前的2个曲面的点云数据图，数据点分别为5 059个、5 353个；图5c和图5d为过滤后2个曲面的点云数据图，数据点分别为581个、497个。过滤后的点云数据大量减少，但从点云图形看，山羊蹄底部 2个曲面的形状特征依然清晰，点云过滤未影响2个曲面的形貌特征。

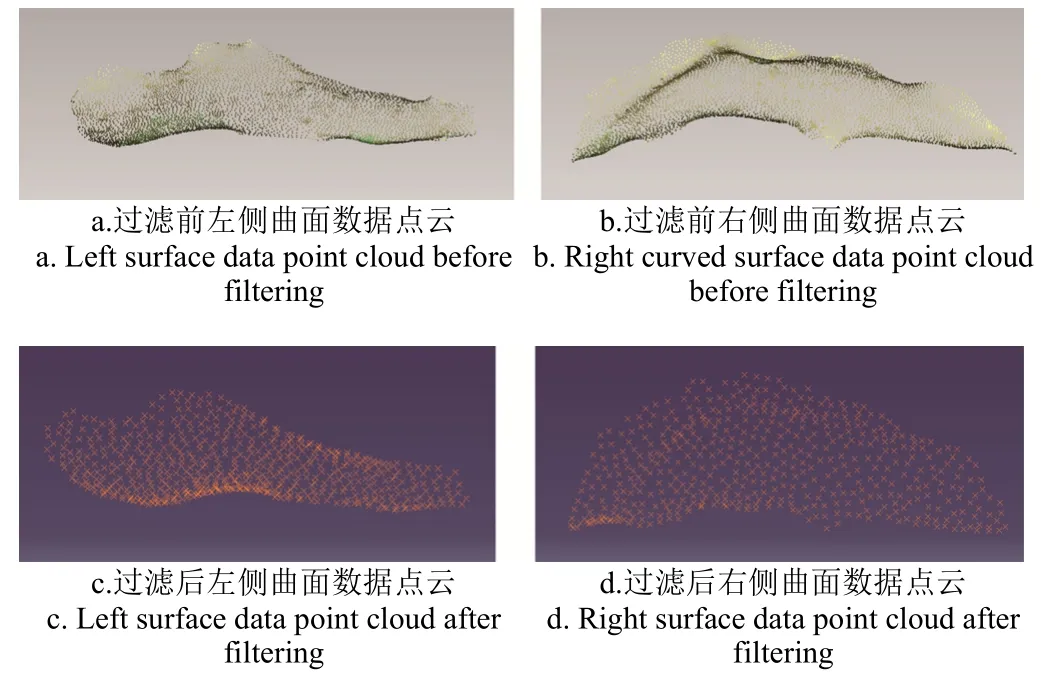
图5 山羊蹄底部2个曲面点云过滤前后对比图Fig. 5 Comparison diagram of 2 curved surface patches at bottom of goat’s hoofs

2 山羊蹄底部曲面数学模型

山羊蹄底部的 2个曲面从外观上看不符合固定的数学模型，因此采用多项式拟合方式对其进行拟合。Matlab 2014自带工具箱（toolboxes），利用工具箱里的曲面拟合（cftool）对点云数据进行多项式拟合。

2.1 山羊蹄底部左侧数学模型

把山羊蹄左侧点云数据导入到 Matlab软件中，以x和y为自变量，以z为因变量，以多项式拟合曲面特征点云。在Matlab软件的cftool拟合模块中，选取多项式进行拟合，同时选择x，y的次幂数，x，y的次幂数值越高，曲面拟合的精度越高，但曲面的复杂程度也越高。由于建立数学模型要用于仿生四足机器人足端上，因此拟合时不仅考虑拟合精度，还要考虑模型复杂程度。精度不高模型失去其原有特征，复杂程度大会增加加工成本，综合2个因素考虑。x，y不同指数的拟合结果如表1所示。

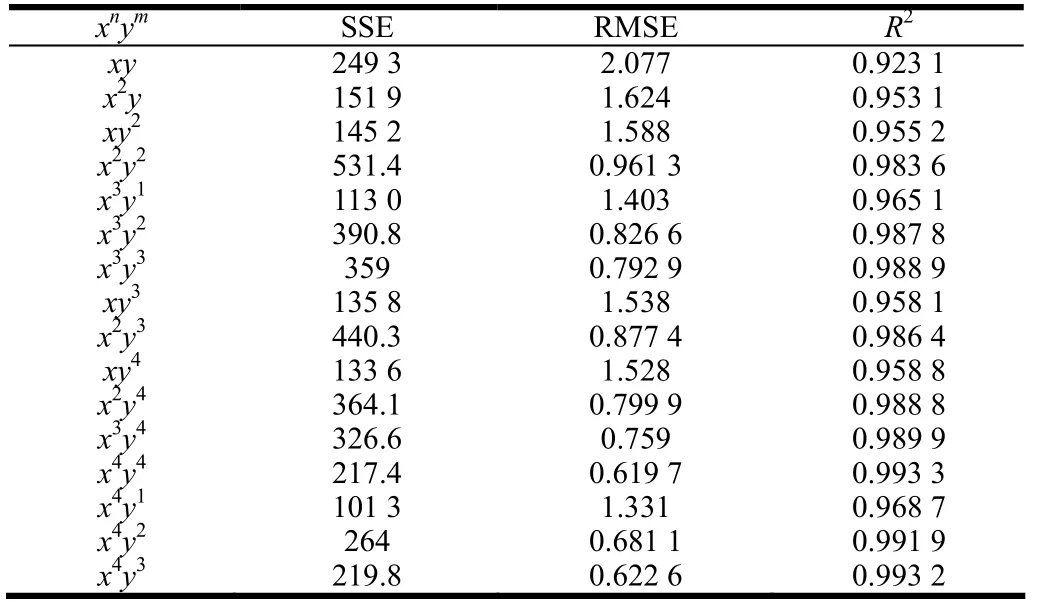
表1 不同指数自变量左侧面的拟合结果Table 1 Fitting results of left side bottom for different index of independent variable

由分析表1可知，随着x和y的指数不断增加，对点云的三维坐标数据进行的Matlab多项式曲面拟合的残差平方（SSE）和均方差（RMSE）的值在不断减小，决定系数（R2）在不断增加，说明随着x，y的指数增大，拟合的曲面越接近实际曲面的形貌特征。但在x，y的指数增大到3以后，每增加1个自变量的指数，SSE、RMSE、R2数值变化不大，如当x，y的指数由x3y3增加到x4y3时，残差平方（SSE）由359减小到219.8，均方差（RMSE）由0.792 7减小到0.622 6，决定系数由0.988 9增加到0.993 2；如当x，y的指数由x3y3增加到x3y4时，残差平方（SSE）由359减小到326.6，均方差（RMSE）由0.7 927减小到0.759，决定系数由0.988 9增加到0.989 9。继续增加次数幂，结果参数会变得更小，但曲面的复杂程度会大大增加。当指数都为 3时，曲面拟合结果为SSE=359，RMSE=0.792 9，R2=0.988 9，决定系数接近1，对于复杂的生物表面拟合结果来说，拟合精度符合拟合要求。综上，x，y的指数都选择3为自变量。山羊蹄左侧曲面的拟合方程为：

残差平方（SSE）=359；均方差（RMSE）=0.792 9；决定系数（R2）=0.988 9。

山羊蹄左侧曲面Matlab拟合曲面如图6所示。

图6 山羊蹄底部左侧拟合曲面Fig. 6 Fitting surface of goat’s left hoof bottom

2.2 山羊蹄底部右侧数学模型

采用同样的方法在Matlab软件中对山羊蹄底部右侧曲面的点云数据进行曲面拟合，同样考虑精度和加工复杂程度。x，y不同指数的拟合结果如表2所示。

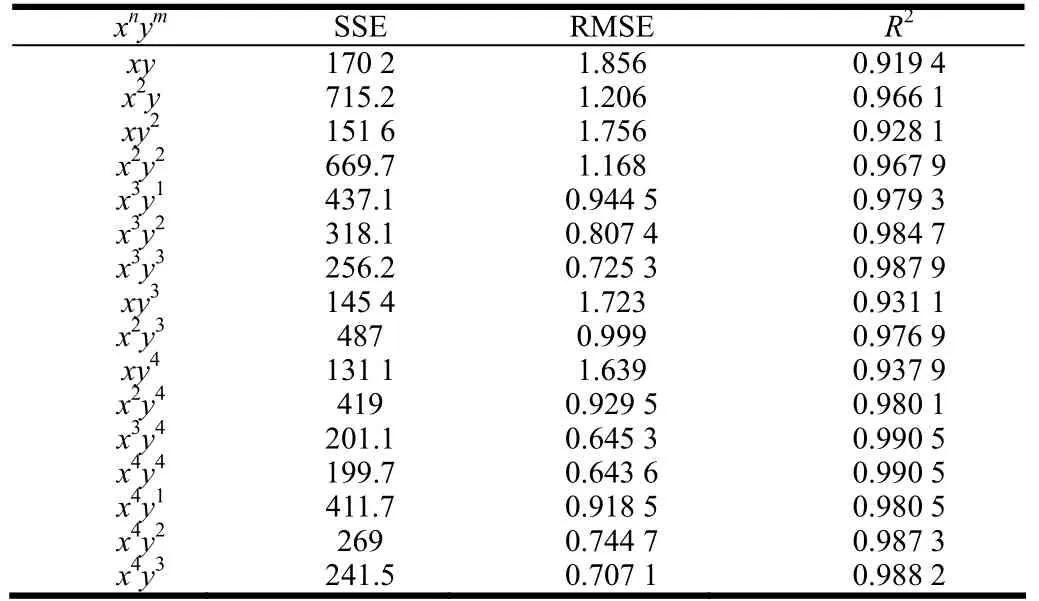
表2 不同指数自变量右侧面的拟合结果Table 2 Fitting results of right side bottom for different index of independent variable

分析表2可知，随着x和y的指数不断增加，拟合的曲面的残差平方（SSE）和均方差（RMSE）的值在不断减小，决定系数（R2）在不断增加，说明随着x，y的指数增大，拟合的曲面越接近实际曲面的形貌特征。但在x，y的指数增大到3以后，每增加1个自变量的指数，SSE、RMSE、R2数值变化不大，如当 x，y的指数由 x3y3增加到x4y3时，残差平方（SSE）由256.2减小到241.5，均方差（RMSE）由0.725 3减小到0.707 1，决定系数R2由0.987 9增加到0.988 2；当x，y的指数由x3y3增加到x3y4时，残差平方（SSE）由256.2减小到201.1，均方差（RMSE）由0.725 3减小到0.645 3，决定系数由0.987 9增加到0.990 5。继续增加次数幂，结果参数变得更小，但曲面复杂程度大大增加。当指数都为 3时，曲面拟合结果为SSE=256.2，RMSE=0.725 3，R2=0.987 9，决定系数接近1，对于复杂的生物表面拟合结果来说，拟合精度较高，符合拟合要求。综上，x，y的指数均选择3为自变量。山羊蹄右侧曲面拟合方程为：

残差平方（SSE）=256.2；均方差（RMSE）=0.725 3；决定系数（R2）=0.987 9。

山羊蹄右侧曲面Matlab拟合曲面如图7所示。

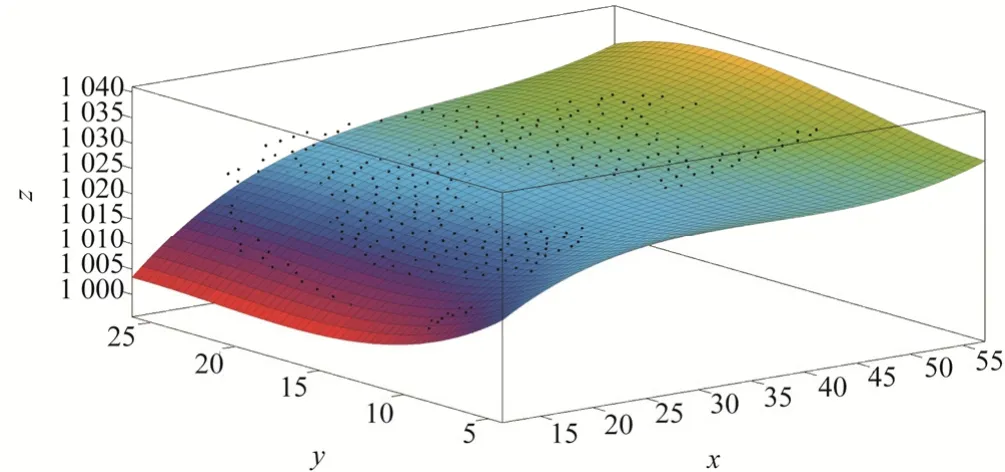
图7 山羊蹄底部右侧拟合曲面Fig. 7 Fitting surface of goat’s right hoof bottom

2.3 数学模型验证

为验证山羊蹄底部非规则曲面数学模型，选取建模之外的同种山羊的 3个蹄作为验证样本，对样本进行喷FA-5反差增强剂并粘贴哑光黑圆点标记点，并用三维扫描仪获取三维点云数据，然后把点云数据导入Geomagic Studio进行点、多边形、精确曲面等一系类处理得到样本三维模型，把得到的特征曲面的点云数据导入到Catia软件的数字化设计（Digitized Shape Editor）模块中，对曲面点云进行处理，并以.txt文件格式导出特征曲面的点云三维坐标。将得到的 3个验证样本的特征曲面的 x和 y坐标值分别代入所建的数学模型中，对数学模型拟合值和原坐标值进行分析得到残差和相对误差，结果如表 3所示。

表3 不同山羊蹄特征曲面模型拟合值与实际值对比分析Table 3 Comparison analysis between fitting values and actual values of characteristic surface of different goat's hoof

分析表3可知，文中所建立的2个数学模型的计算值与实际值的一致性良好，相对误差均小于10%，模型1和模型2的相对误差的最大值分别为8.63%和9.58%，相对误差均值分别为4.32%和4.73%，相对误差均值满足工程设计允许的误差范围±5%[33]，验证了文中所构建的山羊蹄底部非规则曲面数学模型的有效性。

3 结论

1）通过三维扫描仪扫描获取了山羊蹄底部的三维点云数据，通过Geomagic Studio软件对山羊蹄底部点云经过点、多边形、精确曲面处理，对处理结果进行3D偏差分析，偏差最大值范围为-6.098 9～+6.099 6 mm，平均值为-0.856 6～+0.678 3 mm，标准偏差为1.402 2 mm。

2）通过Geomagic Studio软件对山羊蹄底部进行划分，得到山羊蹄底部左侧曲面和右侧曲面，把曲面点云数据导入Catia软件进行过滤并导出点云数据的三维坐标；利用Matlab软件曲面拟合功能，对山羊蹄底部2个曲面的点云数据进行多项式拟合，得出拟合后图形和拟合方程。山羊蹄底部左侧曲面的拟合方程为：