基于数值仿真的泵阀变刚度弹簧设计与优化
2018-08-21董世民
董世民,朱 葛
(燕山大学机械工程学院,秦皇岛066004)
0 引 言
往复泵是一种通用的水力机械设备,在国民经济的各个领域均得到了广泛应用。泵阀是往复泵的重要部件,往复泵泵阀主要采用自动锥形阀结构。弹簧是自动锥形阀的重要组成部分,弹簧的主要作用是平衡惯性力,降低阀盘的落座速度与滞后高度,但是也降低了阀盘升程,增大了阀隙间的水头损失,降低了吸入性能,因此弹簧对往复泵的工作性能影响明显。国内外的许多专家学者在泵阀的工作理论、设计计算和应用方面进行了大量的研究工作[1-9]:阿道尔夫于1968年建立了泵阀运动规律的二阶非线性常微分方程;针对阿道尔夫所建立泵阀运动微分方程在泵阀开启瞬间存在奇点的问题,董世民等[7]综合考虑流体可压缩性与魏氏效应对泵筒与阀隙液体连续流方程的影响,建立了适用范围更广的泵阀运动规律仿真模型;基于泵阀运动规律的数值仿真方法,张慢来等[10-13]分析了弹簧刚度与预紧力对于泵阀运动特性的影响;郑淑娟等[14-19]基于CFD流场可视化技术仿真分析了阀隙流场与阀出流特性;Pei等[20]基于台架模拟试验系统测试了泵阀运动规律。
弹簧刚度与预紧力等泵阀结构参数对泵阀动力特性有显著影响,但目前的研究[10-19]仅限于单因素的仿真分析,基于优化设计理论的泵阀结构参数优化设计方法的研究尚不深入。例如,吴亮等[21-22]基于泵阀最大升程、最大滞后高度与落座冲击速度的简化解析模型给出了泵阀结构参数的简化计算方法。目前,基于流体动力学仿真的优化设计技术已经广泛应用流体机械结构的优化设计[23-26]。
目前往复泵锥阀结构与运动规律的研究都是针对定刚度弹簧的泵阀结构。结合非线性弹簧技术在改善机械系统动态特性领域的实际应用,笔者设计了变刚度系数弹簧的泵阀结构,以达到改善泵阀动力特性与泵吸入特性的目的。本文在建立变刚度弹簧泵阀运动规律仿真模型的基础上,仿真分析变刚度弹簧对泵阀动力特性与泵吸入性能的综合影响,进而建立基于系统动力仿真的变刚度弹簧参数的优化设计方法。
1 泵阀运动规律数学模型的建立
液缸内压力过低时会引起液缸内出现明显的空化现象,降低泵的充满系数,同时泵出口处的流量脉动和压力脉动大幅增加[27-29],因此本文以吸入阀为研究对象,建立泵阀运动规律的数学模型,重点研究阀隙间的水头损失和阀盘运动特性。为便于研究,做如下简化和假设:1)忽略液体在液缸内流动时的沿程阻力损失;2)忽略连杆、活塞以及液缸等元件的弹性变形;3)假设液缸内的液体密度与压力与液缸内的位置无关。
图1与图2分别为往复泵工作原理示意图与往复泵锥阀结构示意图。
1.1 阀盘运动微分方程
往复泵在吸液过程中,活塞由左死点向右运动,液缸内液体膨胀,压力开始降低,当内外压差足以克服弹簧预紧力与阀盘重力时,吸入阀开启,此时阀盘分别受到以下几个力的作用:阀盘下部与上部液体压差作用下产生的举升力、阀盘自身重力、弹簧弹力、液体对阀盘的水力阻力以及阀盘导向爪与阀座之间的摩擦力(摩擦力的作用方向与阀盘的运动速度方向相反),阀盘的运动微分方程为
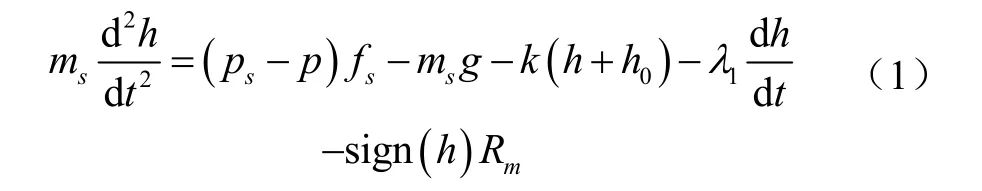
式中 ms为阀盘质量,kg;p为液缸内液体压力,Pa;ps为吸入管内吸入阀口处的液体压力,Pa;fs为阀盘面积,m2;g为重力加速度,m/s2;k为弹簧刚度,N/m;h为阀盘升程,m;h0为弹簧预紧量,m;λ1为阻力系数;Rm为阀座对阀盘导向爪的摩擦力,N;sign(h)为符号函数,当h≥0时,sign(h)=1;当 h<0时,sign(h)= -1;t为时间,s。
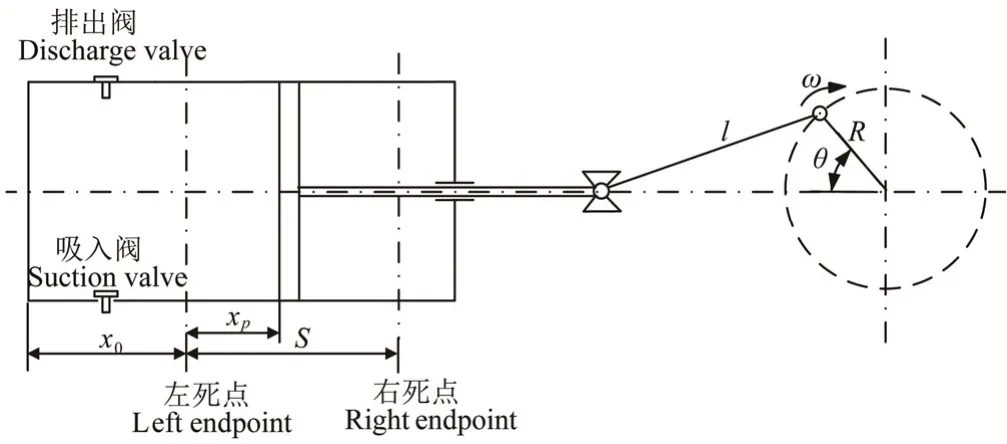
图1 往复泵的工作原理图Fig.1 Working principle diagram of reciprocating pump
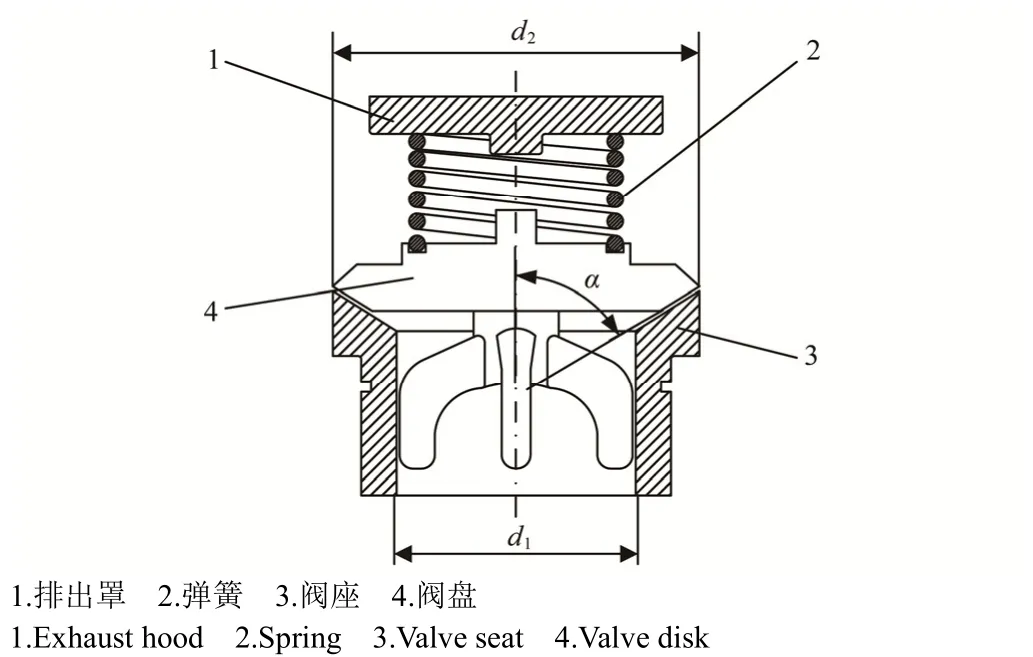
图2 自动锥形阀结构图Fig.2 Structure diagram of automatic cone valve
目前,往复泵锥阀采用定刚度系数弹簧。若弹簧刚度系数随弹簧变形量的变化而变化,则弹簧是变刚度系数弹簧。设弹簧刚度与弹簧变形量之间的函数关系为

式(1)中液体对阀盘的水力阻力、阀座对阀盘导向爪的摩擦力一般较小,忽略这两项力的影响,吸入阀运动微分方程简化为
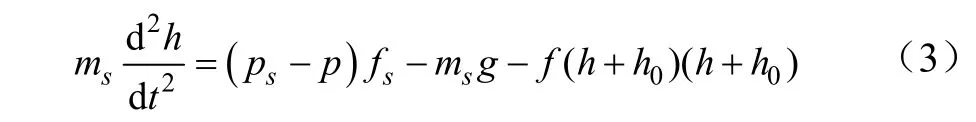
1.2 泵阀阀隙连续流方程
根据单位时间内泵缸内流体质量的增量 dM1应等于经过泵阀阀隙流入泵缸的流体质量 dM2,即可建立流体连续性方程

其中单位时间内泵缸内流体质量的增量 dM1为
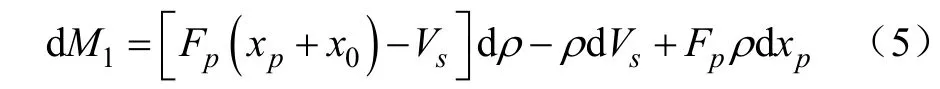
式中Fp为液缸内圆面积,m2;ρ为t时刻液缸内液体的密度,kg/m3;Vs为t时刻阀盘、阀隙与阀座所形成的空间体积且Vs=fsh,m3;xp为t时刻活塞的位移,m;x0为余隙长度,即将余隙容积转化为横截面为Fp的圆柱体所对应的长度,m。
液缸内的液体密度与压力之间的函数关系为
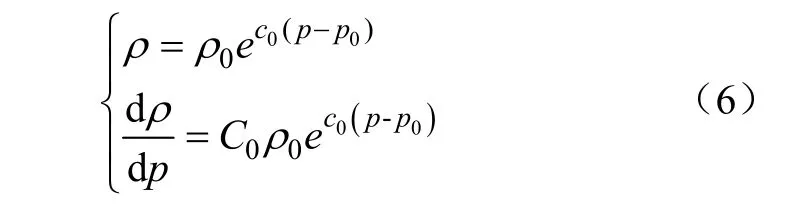
式中ρ0为液缸内液体在标准下的密度,kg/m3;C0为液体的压缩系数;p0为标准压力,Pa。
活塞运动位移xp与速度vp可由式(7)、(8)确定。
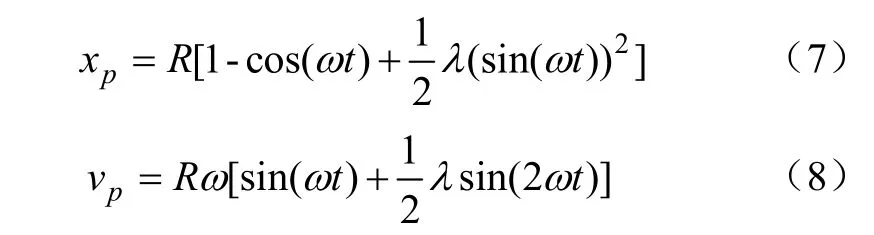
式中λ为连杆比,其中λ=R/l;R为曲柄半径,m;l为连杆长度,m。
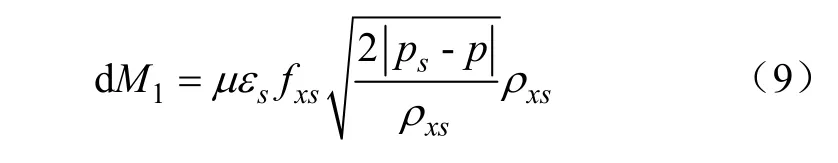
单位时间内经过阀隙流入液缸内的液体质量为式中 μ 为流量系数;εs为系数,εs=±1;ρxs为经过阀隙流动液体的密度,kg/m3;fxs为阀隙的过流面积,m2。
当 Ps-P≥0 时,εs=1,ρxs=ρs(液体在吸入压力 ps条件下的密度);Ps-P<0 时,εs=﹣1,ρxs=ρ。
其中阀隙的过流面积有
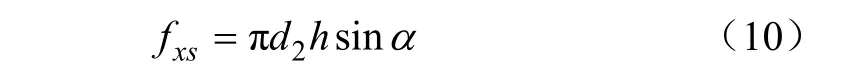
综上推导可有
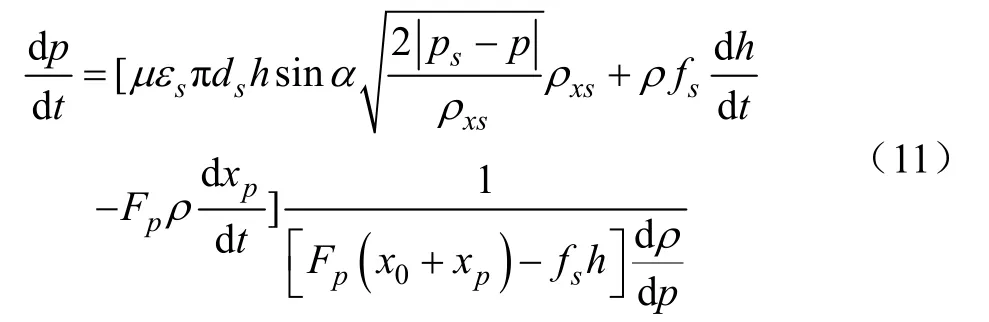
1.3 吸入阀运动初始条件的确定
由于滞后角的存在,活塞运动到左死点时,排出阀并未关闭,阀盘还存在一定的滞后高度,当排出阀关闭时,活塞由左死点向右走过的距离为xod,曲柄转过的对应角度为ψod(排出阀的滞后关闭角)。随着柱塞的继续运动,泵缸内的压强开始逐渐降低。当阀盘的上下压差Δp产生的举升力足以克服阀盘的重力与弹簧预紧力时,吸入阀开启,由此可推导出泵阀的开启压差与开启压力为
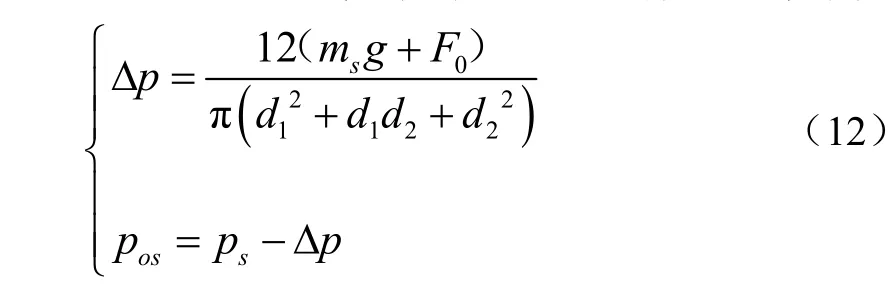
式中F0为弹簧预紧力,N;pos为吸入阀开启瞬间对应的缸内压力,Pa。
而弹簧预紧力F0与弹簧预压量h0满足如下的函数关系为
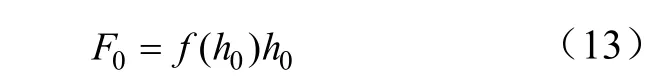
式中f(h0)是弹簧变形量为h0时对应的弹簧刚度。
根据泵缸内液体质量守恒可求得吸入阀打开瞬时的活塞位移xos为
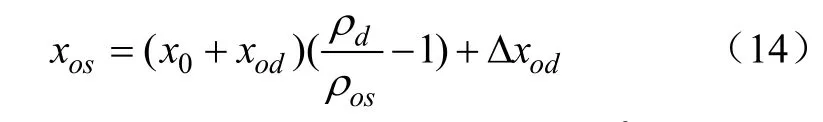
式中 ρd为液体在排出压力 Pd下的密度,kg/m3;ρos为液体在排出压力pos下的密度,kg/m3。
根据活塞位移可求得吸入阀打开时刻ost满足

式中tos为阀盘开启瞬时对应的时间,s。吸入阀运动的初始条件为
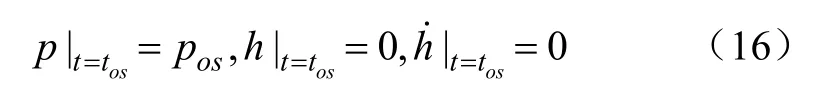
1.4 吸入阀运动规律的数学模型
根据上述建立的吸入阀运动微分方程、泵阀连续流方程以及初始条件,建立了描述吸入阀运动规律的数学模型,可以写成如下的一阶常微分方程组
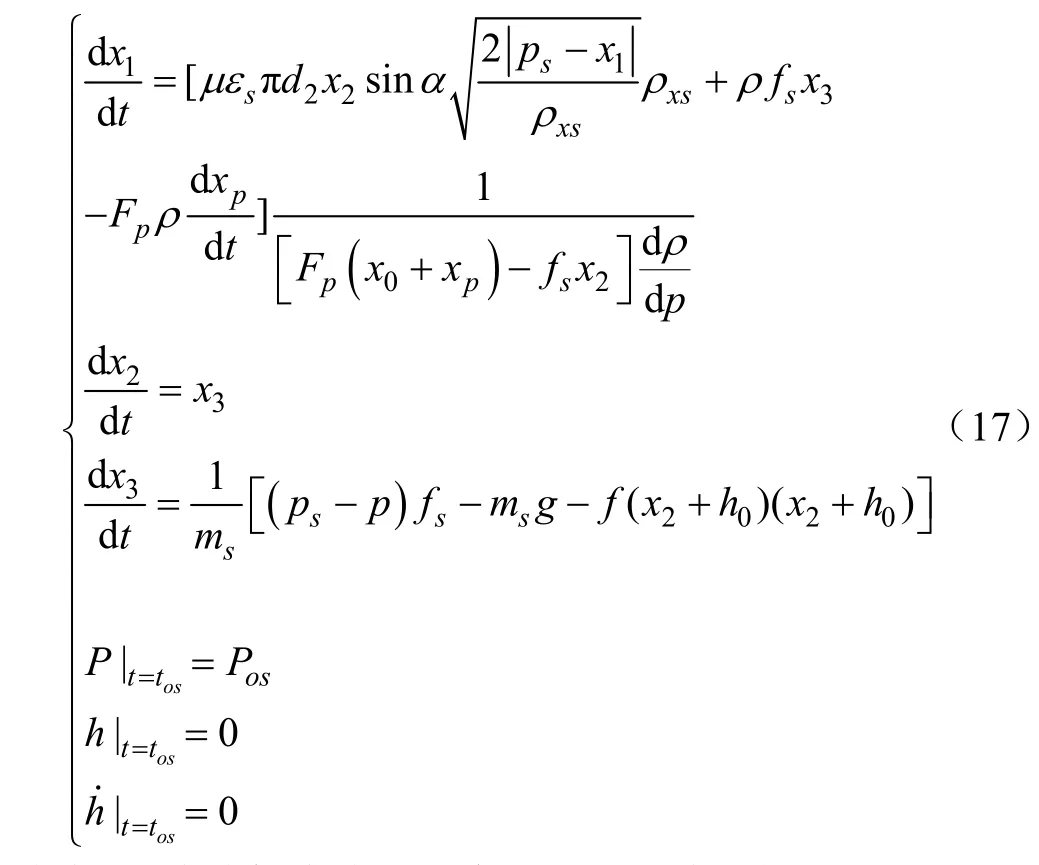
式中 x1为液缸内液体压力,Pa;x2为泵阀升程,m;x3为阀盘的运动速度,m/s。
根据液缸内液体瞬时压力的仿真结果,计算吸入阀吸液过程中阀隙间的最大水头损失为
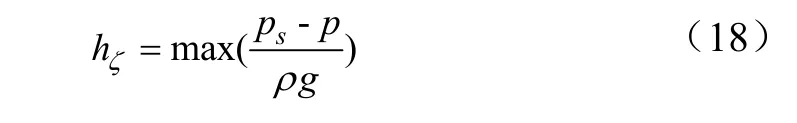
2 泵阀运动规律的仿真计算
2.1 仿真模型精度验证
根据上述建立的弹簧变刚度系数条件下泵阀运动规律的数学模型,本文采用龙格—库塔法建立了泵阀运动规律的仿真模型,并基于Matlab开发了泵阀运动规律仿真程序。为了验证仿真模型的计算精度,利用该程序对油田3NB-1300型钻井往复泵进行了仿真试验,该泵的仿真试验参数为:冲程0.254 m,液缸直径0.170 m,钻井液密度1 100 kg/m3,阀盘质量为4.0 kg,弹簧为普通圆柱螺旋弹簧,刚度系数7 500 N/m,预紧力230 N。
仿真过程中,给定工况参数:排出压力Pd为0.16 MPa,吸入压力Ps为0.13 MPa,冲次为74 min-1。根据式(12)、(14)以及(15)求出吸入阀开启瞬间对应的液缸内压力Pos等初始条件,代入上述建立的泵阀运动规律仿真程序,得到该泵冲次为74 min-1时的阀盘升程、运动速度以及液缸内压力随曲柄转角变化规律的仿真曲线,结果如图3所示。
实际测量过程中,使3NB-1300型钻井往复泵在相同工况条件下运转,使用半导体应变片压力传感器测定液缸内与吸入管内压力,采用阀位移传感器测量阀盘位移,使用自制的测死点装置获得柱塞左、右死点位置,得到吸入阀开启过程中不同转角下阀盘升程的实测结果[7],与仿真结果对比如图3所示。
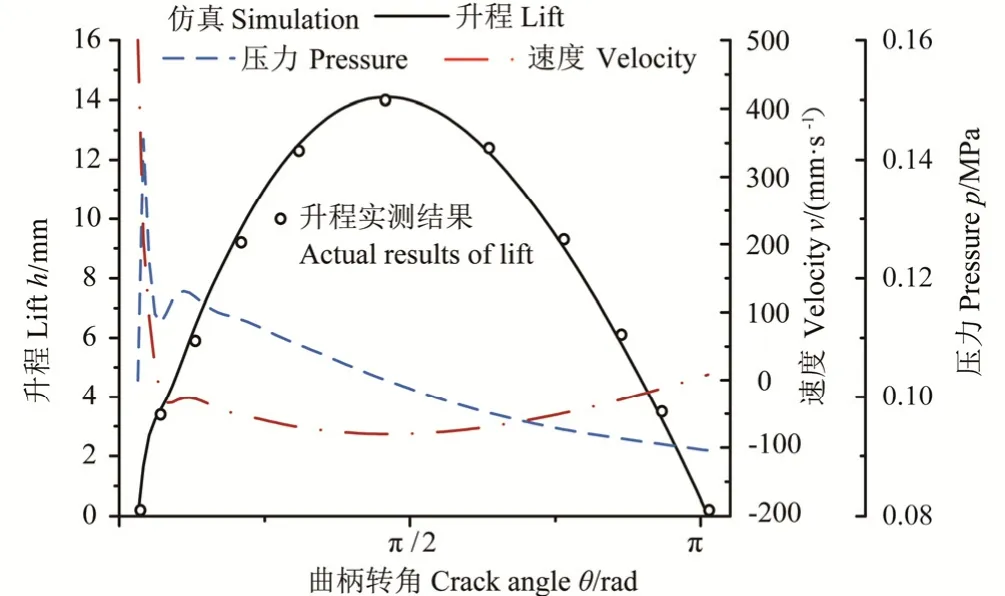
图3 74 min-1冲次阀盘升程、运动速度与液缸内压力曲线Fig.3 Curve of valve disc lift, movement velocity and pressure in liquid cylinder under stroke frequency of 74 min-1
为了进一步验证不同工况条件下仿真模型的计算精度,仅改变冲次参数,分别提取不同冲次下阀盘最大升程仿真结果与实测结果[7]进行对比,如表1所示。
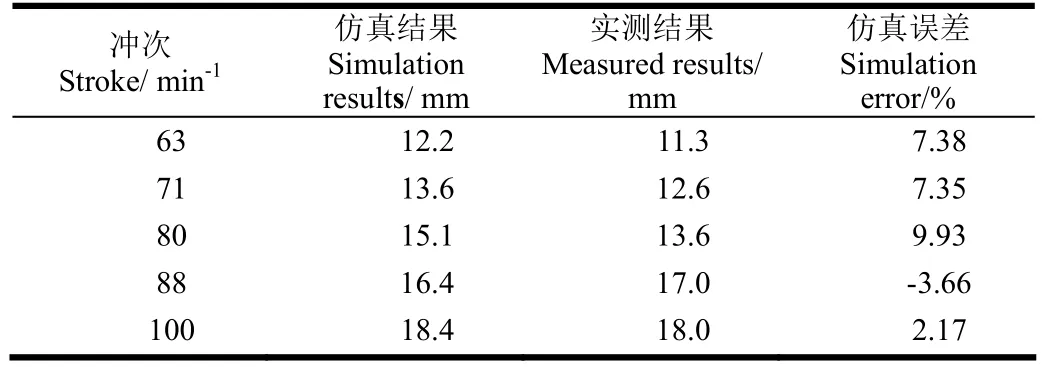
表1 泵阀最大升程仿真结果与实测结果对比Table 1 Comparison between simulation results and measured results about maximum lift
由图3可见,泵阀升程的仿真曲线与实测结果比较吻合,仿真误差小于±8%;对比表1中的仿真结果与实测结果,泵阀的最大升程仿真误差小于±10%,说明上述建立的描述泵阀运动规律的仿真模型基本满足工程实际的精度要求。
2.2 不同弹簧类型泵阀运动规律及吸入性能仿真对比
2.2.1 定刚度系数弹簧仿真试验
图 4为使用定刚度系数弹簧时,不同预紧力与刚度组合条件下阀隙间最大水头损失、滞后高度与阀盘落座速度的仿真图像。

图4 定刚度系数弹簧时泵阀性能仿真结果图4 Simulation results of pump valve performance under constant stiffness coefficient condition
由图4可以得出以下结论:
1)对于定刚度系数弹簧,吸液过程中阀隙间最大水头损失随预紧力与刚度的增大而增大,阀盘落座速度与滞后高度随预紧力与刚度的增大而减小;
2)在所有仿真实例中当F0=100 N,k=1 000 N/m时,流体流经阀隙的最大水头损失最小,仅为1.372 2 m,但此时阀盘的落座速度与滞后关闭高度达到最大;相反当F0=300 N,k=100 000 N/m时,阀盘的落座速度与滞后高度最小,但阀隙最大水头损失最大,达到9.590 9 m。
综上可以看出,阀隙间水头损失与落座速度以及滞后高度的变化趋势相互矛盾,即对于定刚度系数弹簧,很难通过单纯的调节刚度与预紧力的方式达到既降低水头损失又降低落座速度与滞后高度的目的。
2.2.2 变刚度系数弹簧仿真试验
当泵阀采用变刚度弹簧时,吸入过程中液缸内的最低吸入压力、泵阀最大升程、泵阀滞后高度以及泵阀落座冲击速度都是弹簧刚度函数的函数,即都是弹簧刚度函数的泛函。为便于仿真分析以及优化及建模,将弹簧刚度函数式(2)简化为
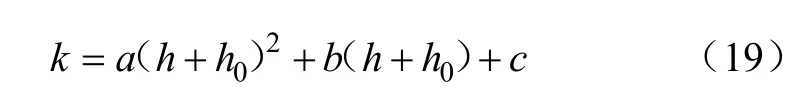
式中a,b,c为常数。
弹簧恢复力与变形量之间的关系可分为以下 3种类型:直线型、渐增型、渐减型。式(19)中,取系数a,b,c的不同组合便可以得到不同类型的弹簧。以下对比仿真不同类型弹簧泵阀的运动参数与阀隙水头损失。仿真计算的弹簧类型以及有关系数见表2,仿真结果如图5所示。
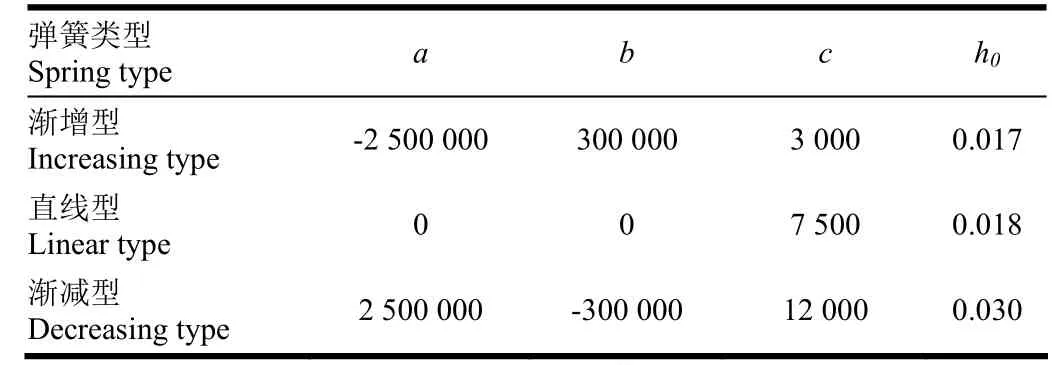
表2 不同弹簧类型仿真参数Table 2 Simulation parameters of different spring types

图5 不同弹簧类型泵阀性能对比Fig.5 Pump valve performance comparison among different spring type
通过以上对不同类型弹簧的仿真试验可以看出: 1)阀盘的落座速度与滞后高度一定时,对比阀隙间的水头损失,渐减型弹簧的最大水头损失最小,吸入性能最好,且在泵阀开启后,渐减型弹簧的水头损失稳定,对于减小液缸内的压力波动也具有一定的作用;2)发现渐减型弹簧的阀盘开启过程中速度较大,开启后的最大升程最大,升程曲线与坐标轴所夹面积最大,有利于降低整个吸液过程中总的水头损失。
3 泵阀变刚度系数弹簧参数优化
由上述仿真结果可知,变刚度系数弹簧对于改善往复泵的工作性能确有一定的作用,下面将基于仿真优化的思想对变刚度弹簧系数进行优化设计。
3.1 设计变量
根据式(19)确定的弹簧刚度与变形量之间的对应函数关系,其中系数a,b,c对于刚度的变化趋势影响明显。此外,常刚度系数弹簧的刚度近似认为恒定,预紧量确定后,预紧力在整个工作过程中不变,但是在变刚度系数条件下,随着弹簧刚度的变化,预紧力部分也随之发生变化,因此对变刚度弹簧进行优化设计时,选取了式(19)中的系数a,b,c以及弹簧的预紧量h0进行优化。
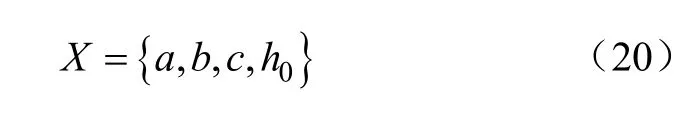
3.2 目标函数
在吸入条件不变的情况下,即吸入口压力恒定时,流体流经阀隙时的水头损失越大,缸内的压力越低,当缸内压力低于流体的空气分离压力或饱和蒸气压时,就有可能引发空化,使往复泵的充满系数降低,影响往复泵的工作性能。因此本次优化选取吸入阀阀隙间的最大水头损失为目标函数。
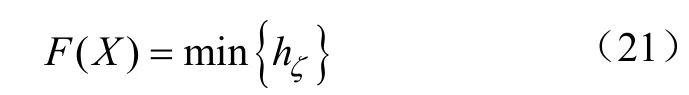
3.3 约束条件
泵阀的质量和它的关闭速度会形成机械动能,在泵阀关闭的瞬间会对阀座造成冲击,由于泵阀经常处于启闭交替地工作状态,启闭比较频繁,因此,在泵阀设计中除了要满足静压下的强度校核,还要特别注意泵阀的关闭速度。根据阿道尔夫无冲击理论,当阀盘的落座速度小于允许关闭速度时,就可近似认为不产生冲击,即对阀盘的使用寿命影响不明显[30]。所以,控制阀盘的允许关闭速度对泵阀设计至关重要,其中泵阀的允许关闭速度是根据阿道尔夫的试验结果最终确定的,即
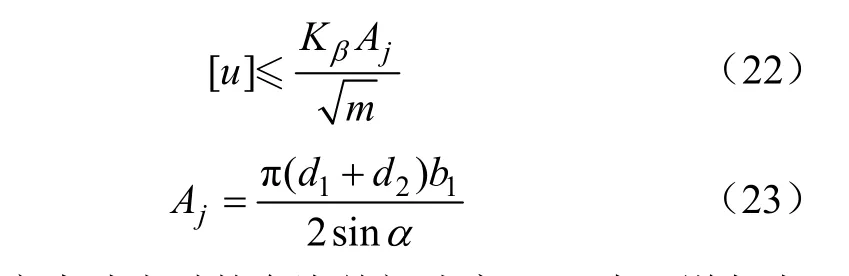
式中[u]为不产生冲击时的允许关闭速度;Kβ为阿道尔夫试验系数;Aj阀盘与阀座接触面积;m阀盘质量;d1为阀盘直径;d2为阀座孔直径;α为阀盘锥角;b1为阀座壁厚。
此外,弹簧预紧量、预紧力以及阀盘升程最大时的弹簧力必须为正值因此约束条件即为
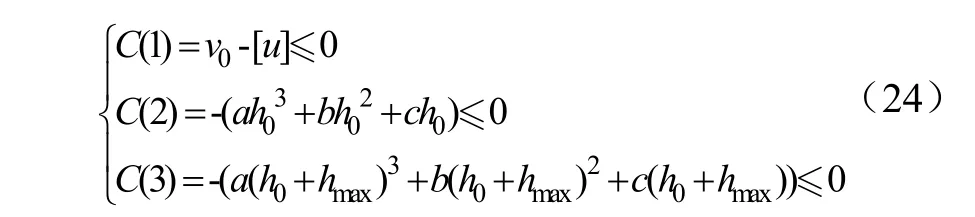
综合上述目标函数和约束条件,基于数值仿真的变刚度弹簧参数优化设计数学模型为
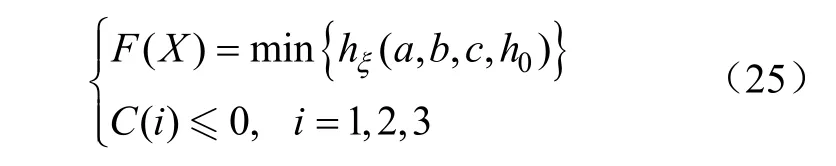
3.4 仿真与优化实例
使用2.1中的仿真参数,计算[u]时,取阿道尔夫试验系数 Kβ=1.30,b1=0.5 cm,由式(23)计算出 Aj=20.2 cm2,由式(22)可以计算出泵阀的允许关闭速度[u]=10.1 cm/s。调用仿真优化程序,采用遗传算法与模式搜索综合的智能优化算法进行求解,将优化结果与传统设计方案中的常刚度系数弹簧进行对比,对比结果如表 3所示,图 6为优化后的变刚度弹簧与定刚度弹簧泵阀性能对比曲线。
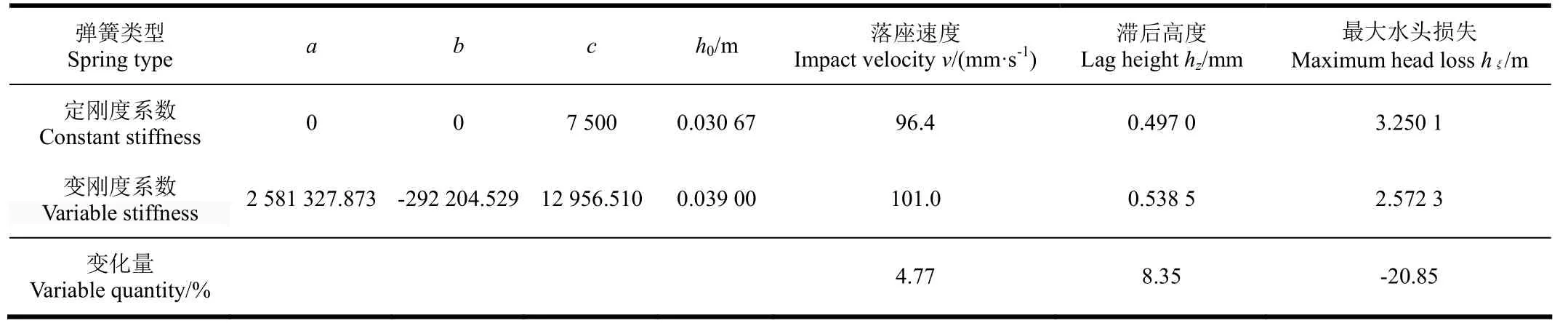
表3 变刚度系数弹簧优化结果与定刚度系数弹簧性能对比Table 3 Comparison of variable stiffness spring optimization results constant stiffness coefficient spring
由以上的仿真曲线可以看出,在限定阀盘的落座速度满足无冲击条件时,优化后阀隙间的水头损失明显降低,其中最大水头损失远低于定刚度系数弹簧。由表 3可以看出,与使用传统设计方法确定的定刚度系数弹簧泵阀相比,使用变刚度系数弹簧后,阀隙间最大水头损失降低幅度达到了20.85%,即液缸内压力得到显著提升,对于避免液缸内流体发生空化,提高往复泵的吸入性能具有重要意义。
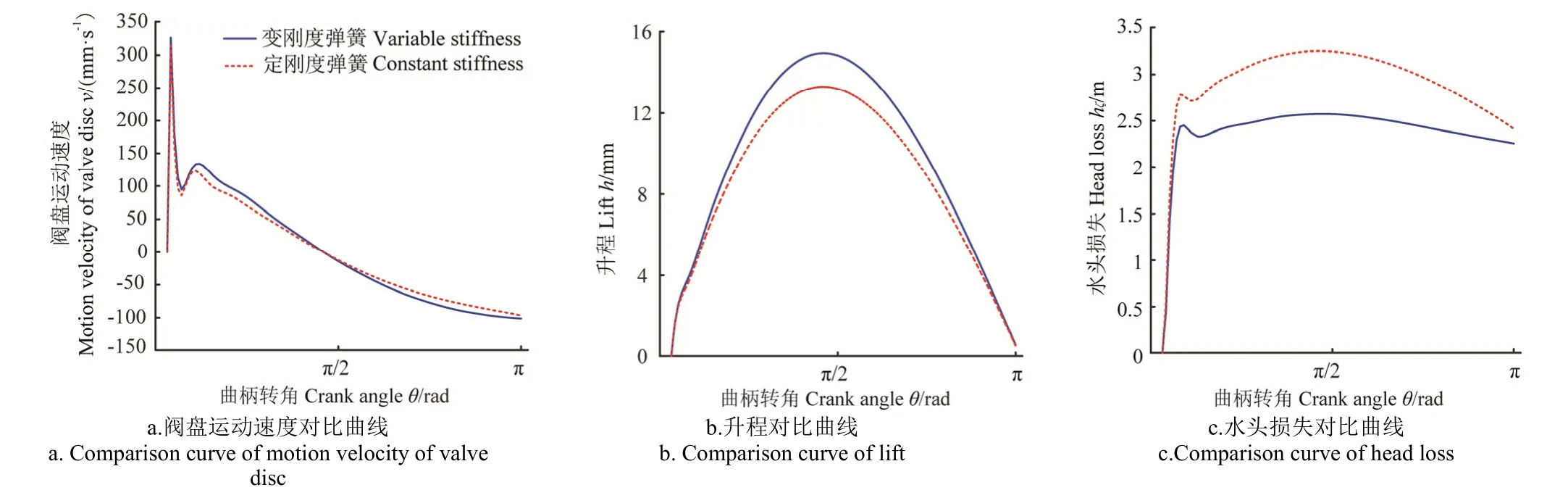
图6 优化后泵阀性能对比Fig.6 Pump valve performance comparison after optimization
4 结论与讨论
本文建立了弹簧变刚度系数条件下泵阀运动规律的数学模型,分别比较了定刚度系数弹簧与变刚度系数弹簧对泵阀性能的影响,并提出了基于数值仿真的变刚度系数弹簧参数优化方法,对变刚度系数弹簧进行了优化设计,得到如下结论:
1)渐减型变刚度系数弹簧可以在不增加落座速度与滞后关闭高度的同时,降低阀隙间的最大水头损失,提高往复泵的吸入性能。
2)优化后,在满足无冲击条件下,阀隙间最大水头损失降低了20.85%,说明变刚度系数弹簧在往复泵泵阀上的应用具有一定的工程实际意义。
针对优化后变刚度系数弹簧与定刚度系数弹簧对泵阀性能的影响,本文仅就数值仿真结果进行了初步对比,具体试验验证部分还需进一步完善。
