基于改进PSO-RBF算法的纯电动汽车剩余里程实时预测∗

陈德海，任永昌，黄艳国，华 铭

前言

电动汽车具有低污染、低噪声的显著特点，使之引领未来汽车工业的发展，电动汽车剩余里程的预测是关键技术之一。根据国家标准法规(EV863)规定，剩余里程指汽车在当前情况下保持现有驾驶模式还能继续行驶的里程。电动汽车剩余里程不仅与动力电池的剩余电量有关，而且还受到外部驾驶环境的影响，因此其预测须融合二元因素。电动汽车的剩余里程与电池端电压、放电电流、电池温度、非必要耗能、坡度系数和循环次数等因素有关。纯电动汽车剩余里程是用户最关心的参数之一，它能有效消除驾驶人因担心剩余里程达不到目的地而产生的里程焦虑[1]，因此精确、迅速、稳定地预测电动汽车剩余里程具有重要意义。

目前对纯电动汽车剩余里程(Sre)的预测算法主要分两大类。第一类，间接预测，具体又分两种:(1)Sre≈f(SOC)≈f(OCV)，只考虑单一影响因素，通过检测端电压Ub间接得到其开路电压OCV，再间接得到其SOC，最后根据SOC值来估算出剩余里程，此类方法比较简单快捷，但是误差很大，最大达到18%，在剩余电量后期甚至超过30%；(2)Sre≈f(SOC)，综合考虑影响因素，通过预测SOC间接估算其剩余里程，SOC类比燃油汽车的燃油量，但电动汽车的SOC受电池端电压、充放电电流、电池温度、循环次数和均衡效应等因素影响，难以直接检测，此类方法在产业界普遍使用，但该方法与真实工况有差别，存在一定误差。第二类，直接预测(Sre(因素))，根据真实工况，检测剩余里程的表征参数，比如剩余电量、标准里程、坡度系数(路况)、载荷和车载设备耗电量等，融合电池包内部参数和驾驶环境外部参数二元因素，建立数学模型直接预测剩余里程，此类方法误差较小，但数学模型复杂、计算量大、硬件设备要求高、成本相对较高。文献[2]中基于电动汽车的高效的能量最优路径而建立续驶里程预测模型。文献[3]中基于动力电池能量状态估计与车辆能耗之间的映射关系而建立续驶里程预测模型。文献[4]中基于模糊能耗与卡尔曼滤波相结合，在识别工况基础上建立剩余续驶里程估算模型。文献[5]中基于动态交通信息的电动车辆剩余里程估算方法而建立预测模型。针对现有方法误差大、自适应性差、数学建模复杂的不足，本文中基于改进的PSO-RBF法对纯电动汽车剩余里程的实时预测进行研究。

1 问题描述与数学模型

影响剩余里程的因素有很多，且其具有时变、非线性的特点。由于多数电动车使用者驾驶路线和用车环境变化较小，因此本文中限定在固定、常用的用车环境中采集数据训练模型，定义动态自适应的标准容量和标准续驶里程，它根据历史状态和工况环境改变而改变。由复杂、非线性的影响因素建立优化PSO-RBF神经网络预测模型，而由易于建立数学模型的影响因素建立应用场景数学模型，用后者对前者加以修正。

1.1 标准RBF

1988年，Broonhead和Lowe利用神经学和数学原理进行优化改进从而建立径向基神经网络(radial basis function，RBF)。它具有BP神经网络很强的泛化能力和线性系统的快速响应特性，同时具有学习速度快、结构简单和最佳逼近特性，无局部极小值，非常适用于非线性的在线实时预测。RBF网络具有3层，如图1所示。

图1 径向基神经网络结构

图1 中:x1…xM为输入层的输入，q1…qq为隐含层的输入，y1…yL为输出层的输出；wij为输入层到隐含层的加权系数，wki为隐含层到输出层的加权系数。RBF的学习过程分为无教师学习阶段和有教师学习阶段。隐含层的输出为

式中:δi为第i个隐节点的标准化常数；ci为第i个隐节点的高斯函数的中心向量；xM为输入层的输入向量。隐含层到输出层是线性映射，输出层的输出为

式中:wi为第i个隐节点到输出层的权系数，运用最小二乘法拟合得来。计算训练的总误差为

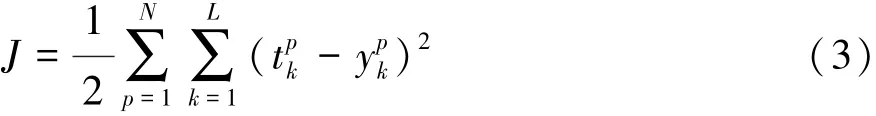
RBF神经网络优点是速度快、结构简单和无局部极值点，缺点是3个参数q，ci和δi无法确定[6]，目前一般运用计算机选择、设计和再检验等试凑法，盲目性高、效率低。

1.2 标准PSO法

粒子群优化(particle swarm optimization，PSO)算法是群体智能算法的一种，其原理是模仿鸟类觅食行为，通过个体和集体的相互竞争来寻找最佳觅食途径，达到快速寻优目的[9]，它具有模型简单、速度快等特点，广泛用于最优化问题。主要分为惯性部分、个体影响部分和社会影响部分，数学模型如下。

设在D维空间中，有N个粒子。粒子i的位置为 xi＝(xi1，xi2，…xiD)，将 xi代入适应函数 f(xi)求适应值；粒子 i速度为 vi＝(vi1，vi2，…viD)；粒子 i个体经历过的最好位置为 pbesti＝(pi1，pi2，…piD)；种群所经历过的最好位置为 gbest＝(g1，g2，…gD)。

粒子i的第d维速度更新公式:

粒子i的第d维位置更新公式为

经过PSO聚类算法初步得到RBF样本输入的隐节点高斯函数的中心向量ci和标准化函数δi，为接下来运用改进的PSO-RBF神经网络做铺垫:

式中:dik＝min(‖zi-zj‖)，j＝1，2，3，…，n，i≠j，为粒子i到最近中心向量 ci的距离；dspk＝为所有粒子到类中心向量的距离

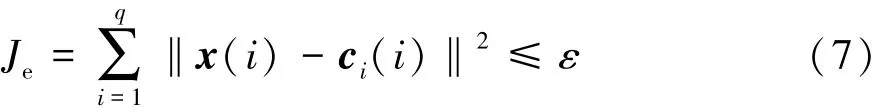
电动车剩余里程的预测具有非线性、时变的特性，随着循环次数、行驶状况不同，预测模型参数须具有动态自适应性。

利用PSO对RBF进行聚类，可以同时具有二者最佳逼近特性、无局部极小值、快速、准确的优点[10]。PSO 3个参数w，c1和c2对其搜寻性能有很大影响，因此参数选择至关重要[11]。参数选择目前主要有固定和时变两大类:前者模型简洁，运行速度快，但精度不高，易陷入局部极值，自适应性差；后者模型复杂，运行速度慢，但是精度较高，具有一定的自适应性。为了同时具有二者的优点，避免其缺点，建立固定和时变相结合的模型。在不同状态下各个参数的不同组合能达到不同的预测效果，本文中综合考虑了各个参数组合下的预测精度和计算速度，计算出参数的界限，设计了一种固定值和时变值组合的参数组合，根据训练样本的总误差，优选出效果最好的一组参数，作为训练结果。为此，引入改进的PSO-RBF法。

1.3 改进的PSO-RBF法

在上述3个参数w，c1和c2中，惯性参数w相对比较容易确定，它应随着寻优迭代次数不断递减，学界普遍认为范围为和，表征粒子群的分散程度。聚类效果为

式中:wmax为最大惯性权重；wmin为最小惯性权重；run为当前迭代次数；runmax为算法迭代总次数，为了计算模型简洁，通过前期训练按比例优选出一定数量的wm(m＝1，2，3…)固定值。至于c1和c2经过大量试验表明c1＝c2＝15时寻优效果比较好，因此把其作为初值，其边界范围为 0.5≤c1≤2.5，0.5≤c2≤2.5，变化步长为0.1。惯性参数w每改变一次，将c1和c2按其变化范围，分别选取不同数值进行训练，根据结果确定该w下效果最好的c1和c2参数组合。然后再由式(7)优选出误差最小的PSO参数组合w，c1，c2，最后再根据PSO聚类算法得到RBF的参数组合q，ci，δi作为模型最终训练结果。

1.4 计算非必要设备能耗

纯电动汽车的非必要能耗设备如空调、灯饰、音响之类因为会消耗电量，影响剩余里程的预测，但此类因素具有偶发性，不能作为改进的PSO-RBF预测模型的参考输入，因此需要另外根据应用场景建立能耗数学模型来修正，解决其建模复杂的难题。剩余里程与剩余SOC之间具有近似线性的映射关系，在标准里程确定的情况下，二者近似成正比关系。因此可以在标准里程SN和标准容量SOCN一定的前提下，把容量参数和耗能功率参数都转化成里程参数。

标准里程SN:城市道路循环工况(CYC＿UUDS)下测量出其标准里程值，电池容量或道路坡度里程每达到一次设定值时更新一个末值:

式中:SN1，…，SNn为在 CYC＿UUDS工况下测试得到的标准里程，n表示测试次数，最后求平均数SN，为了使SN同时具有自适应性和抗波动性，n等于15。

标准容量SOCN:为减小SOC累积误差，使其具有动态自适应性，温度或循环次数每达到设定值一次时更新一次末值:

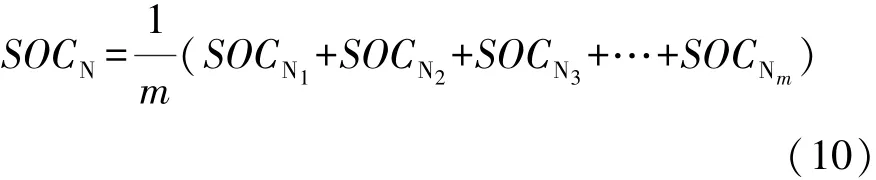
式中:SOCN1，…，SOCNm为在定期测试的标准容量，m表示测试次数，最后求平均数SOCN，为了使SOCN同时具有温度和循环次数自适应性和抗波动性，m取为5。

车载非必要设备能耗里程参数的转化:电动汽车其他必用设备已经考虑在标准里程SN和标准准容量SOCN里，因此不会干扰剩余里程的预测，不必再计算。把非必须耗能设备的总额定容量累积后再转化成里程值Scon:

式中:Scon为非必要耗能设备转化而来的里程值；INk为其第k个额定电流，为已知参数；tk为其第k个耗能时间；η4为转折损系数，由试验测得。

1.5 数学模型

影响电动汽车动力电池剩余里程预测的因素很多，其中，内部因素主要是电动汽车电池的表征参数，如电池端电压、充放电电流、电池温度和循环次数等；而外部因素，有已行驶路程、道路坡度和车载设备的耗能等。为精确、迅速、稳定地预测电动汽车剩余里程，优选内部因素电池端电压Ub、电流I和外部因素载荷、车载非必要设备能耗(空调、音响、灯饰等)和已行驶路程作为预测剩余里程的表征参数。虽然路况系数对电动汽车剩余里程的影响也较大，但本文中限定的是一定范围内的熟悉、规律的日常生活的电动汽车应用场景，在训练预测模型时已考虑该参数因素，为简化模型，不再把该因素作为模型参考输入。改进的PSO-RBF法模型如图2所示。

图2 改进的PSO-RBF法模型

图2 中，改进的PSO-RBF法模型的输入为端电压Ub、端电流Ib、温度 T和载荷 L，输出为 Sre(剩余里程)，并归一化处理(0＜Sre＜1)以减小误差，根据总误差优选出最佳参数组合，作为训练结果。

由于影响剩余里程预测的主要有与电池包有关的内部因素和与行车环境有关的外部因素，因此分两部分建立预测剩余里程模型，前者利用改进的PSO-RBF预测得到，后者利用固定的、常用的应用场景数学建模公式(式(11))来预测，因此总的预测模型为

1.6 剩余里程预测流程

步骤1:以EV-1型纯电动车为试验对象，在UDDS工况下，分别采集数据 Ub，Ib，T，L和已行驶里程S，然后随机选择1 500组数据作为预测值和测试值。为减小误差，对所有数据进行归一化处理。

步骤2:初始化参数，设置PSO粒子群数N＝60，惯性参数w＝0.9，学习参数c1＝c2＝1.5，最大迭代次数为200，误差小于设定值时停止。

步骤3:根据式(3)计算每个粒子的适应度值，再与该组的下一个粒子的适应度值进行比较，如果大于它更新位置，否则不予更新，检索出该组适应度值最小的粒子的位置作为局部极值pbesti。同样方法计算出所有组适应度值，再检索出适应度最小的粒子的位置作为全局极值gbesti。

步骤4:经过PSO聚类算法得到pbesti和gbesti后，初步得到RBF样本输入的隐节点高斯函数的中心向量ci和隐节点数q，再由式(6)分别得到δi，建立并训练改进的PSO-RBF预测模型。最后按条件更新SN和SOCN。

2 试验测试与分析

利用试验数据进行训练和测试，建立4个输入、1个输出的改进的PSO-RBF模型，训练、测试并与标准RBF，PSO-RBF做比较。

2.1 仿真

在Matlab平台上利用式(13)非线性SIF函数和式(14)逻辑时间序列函数产生1 500个非线性的函数数据对，750组作为训练，另外750组数据作为测试，利用该函数来测试算法的拟合性能。本文算法分3部分编程计算:第1部分确定PSO参数，第2部分确定RBF参数，第3部分进行RBF学习训练。试验结果如表1所示。表中的学习时间只包括第3部分所耗时间，不包括前两部分确定参数所耗时间。

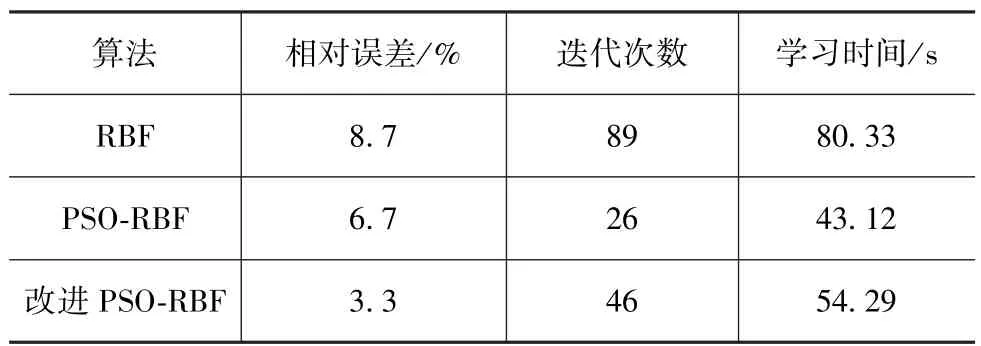
表1 3种方法拟合效果对比

通过表1中3种方法的对比可以得出，改进的PSO-RBF模型的相对误差有了明显降低，迭代次数和学习时间介于二者之间，验证了该优化方法的可行性。

2.2 试验测试

以EV-1型纯电动车为试验对象，依据《电动汽车能量消耗率与续驶里程试验方法》，以40km/h车速进行等速试验，为防止过放电损害电池包，在SOC等于0.02时停止试验，再次充电并静置12h，消除内部极化现象后再继续，重复以上试验。在UDDS工况，分别采集Ub，Ib，T和L，以及能耗设备的启动与运行时间t和实测剩余里程S∗。随机选择1 500组数据作为参数预测得S值，并与相应的试验值S∗做比较。为减小误差，对所有原始数据进行归一化处理。

对RBF法、PSO-RBF法与改进的PSO-RBF法预测剩余里程进行对比。图3和图4分别为基于改进的RBF-PSO法优化的剩余里程预测结果和相对误差，最大相对误差为3.8%；图5为基于RBF法的预测结果，最大相对误差为9.9%；图6为基于PSORBF法预测结果，最大相对误差为6.2%。通过以上3种剩余里程预测法对比，改进的RBF-PSO算法的最大相对误差大幅减小，预测精度有所提高，结果表明改进的PSO-RBF算法预测效果相比其他两种算法有明显改善，证明该预测方法具有显著的优化效果。

图3 改进的PSO-RBF法预测剩余里程

图4 改进的PSO-RBF法预测相对误差

图5 RBF法预测相对误差

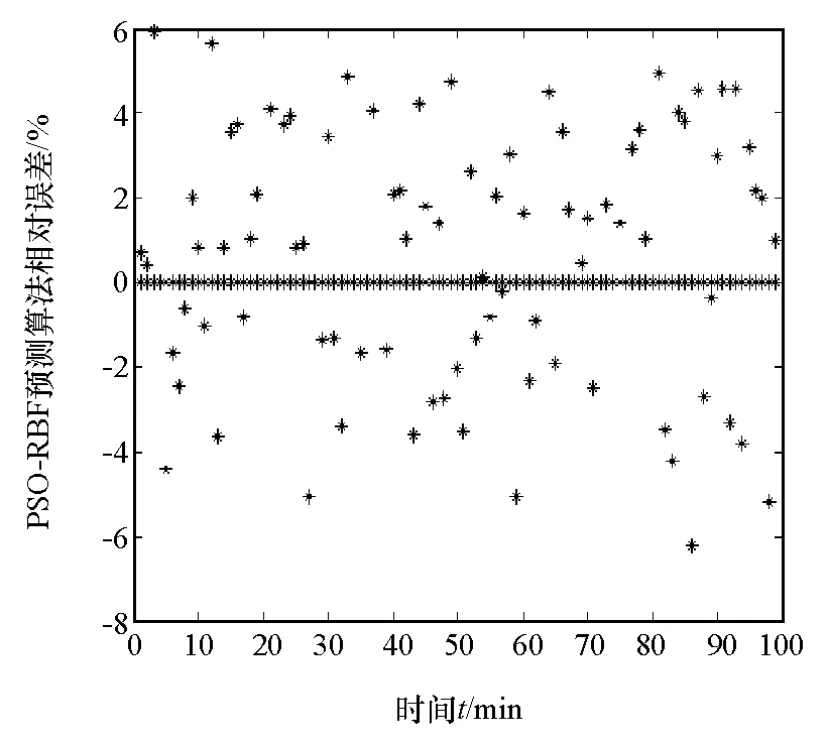
图6 PSO-RBF法预测相对误差

3 结论

利用改进的PSO-RBF算法解决标准RBF法的神经网络隐含层中隐节点数量q，隐节点高斯函数中心向量ci和标准化常数δi难以确定的缺点，融合影响剩余里程内、外部二元因素建立预测模型，解决了剩余里程预测误差大、自适应性差、数学建模复杂的难点。经仿真和EV-1型纯电动车试验测试，优化效果有明显提高，验证了基于改进的RBF-PSO法预测电动汽车剩余里程的优化的可行性。