基于改进K＿means的发动机状态评估方法

谷广宇，刘建敏，乔新勇

前言

发动机作为装甲车辆的心脏，其技术状况的优劣直接影响车辆性能和战斗力，因此如何科学有效地评估发动机技术状况，已成为部队关注的重点。目前，我军在装甲车辆发动机技术状况评估方面，已经做了部分研究[1-2]，然而这些研究主要集中在根据先验样本数据建立评估模型，对未知样本进行评估，而对于在没有先验知识的情况下，如何确立发动机各技术状况等级的划分基准的研究，仍相对缺乏。

现有对发动机状况等级基准划分的研究中，文献[3]中提出了将发动机根据摩托小时划分技术状况阶段，再拟合各阶段的平均值确定相应等级的评估基准。文献[4]中提出了利用主成份分析法根据散点图分布划分技术状况区域，再通过神经网络建立评估模型。这两类方法解决了没有先验知识的情况下有效评估发动机技术状况的问题，但无论是以摩托小时进行阶段的划分，还是以散点图分布进行区域划分，都存在很大的主观因素，不同的划分标准也会对最终的评估结果造成很大影响。由于环境条件、工作强度等因素影响，发动机的实际技术状况存在很大随机性，不同样本下建立的评估基准与评估模型可能存在较大差异，并且由于受试验成本、试验周期等条件的限制，通常无法进行大量试验来获取大样本，这也会增加样本随机性对评估模型的影响，难以保证其最终得到评估结果的可靠性。

为解决上述问题，本文中通过改进K＿means聚类算法，利用试验样本数据分布，计算各等级聚类中心及其分类，建立更加客观稳定的评估模型，实现基于数据驱动的发动机状态评估，并融合Bootstrap小子样统计方法，利用其通过再生抽样将小样本问题转化成大样本的特性，削弱试验样本随机性对评估模型的影响，增强发动机评估模型的稳定性。

1 K＿means算法

K＿means算法是一种典型的基于划分的聚类算法，属于无监督机器学习方法的一种。该算法将一个含有n个样本的集合划分为K个子集合，其中每个子集合代表一个类簇，同一类簇中的样本具有高度的相似性，不同类簇中的样本相似度较低。

1.1 K＿means算法基本思想

K＿means算法的基本思想是:首先从n个样本集中随机选择K个样本作为初始聚类中心，根据每个样本与各个聚类中心的相似度，将其分配给最相似的聚类中心，得到K个互不相交的类簇集合；然后重新计算每个类簇的新中心，再将每个样本根据相似性原理分配给最近的簇中心，重新计算每个类簇的新中心，分配每个样本到距离最近的类簇。这个过程不断重复，直到各个类簇的中心不再变化，得到原始样本集合的K个互不相交的稳定的类簇。

该方法在聚类过程中采取距离就近原则，将数据样本中的每个属性变量统一看待，而忽略了每个属性在聚类分析过程中对于数据样本划分的不同重要性。例如在发动机状态评估中，特征序列与使用时间序列的相关性越大，表示特征参数随使用时间逐渐劣化的趋势越明显，用来评估发动机技术状况优劣的效果越好，在聚类过程中应给予相应重视。

由于K＿means算法是一个局部搜索过程，其聚类结果依赖于初始聚类中心和初始划分[5]，因此本文中提出基于加权欧氏距离最小方差优化初始聚类中心的K＿means改进算法。

1.2 K＿means算法一般过程

在K＿means算法中，对于待聚类的数据样本X＝(x1，…，xn)和 K 个初始聚类中心 C1，C2，…，CK，基本定义如下。

样本xi与xj间加权欧氏距离:

样本xi到所有样本的平均距离:

样本xi的方差:

数据样本的平均距离:

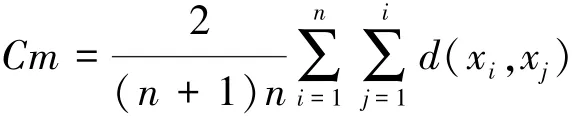
聚类误差平方和:

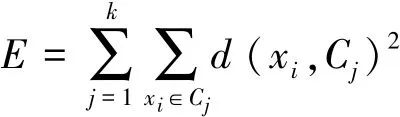
其一般过程如图1所示。

图1 K＿means算法一般流程

2 算法改进

2.1 相关性加权欧式距离

在传统聚类算法中，按样本间相似度进行聚类划分通常以欧氏距离为准，即

为了反映特征序列与使用时间序列的相关性，通过对多种赋权法的比较[6]，提出了基于特征序列相关性指标的定权方法。相关性指标是在相关系数的基础上提出的，以取绝对值的方法将其限定在[0，1]区间，表征了特征序列与使用时间间的线性相关程度。某个特征序列的相关性指标值越大，其与使用时间的线性相关性也越大，从而该特征也能更好地描述发动机技术状况从优到劣的变化过程。该方法权重计算步骤如下。

对于样本数据的第i个特征序列，其相关性指标是其相关系数的绝对值，即

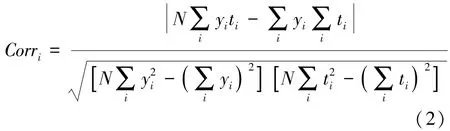
式中:Corri为第i个特征序列的相关性指标；Y＝(y1，y2，…，yN)为第 i个特征序列；N 为检测次数，即序列长度；T＝(t1，t2，…，tN)为相应时间序列。 根据样本所有属性的变异系数，计算各属性的权重:

此时计算样本间相似度可采用加权欧氏距离:

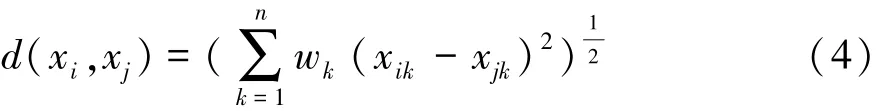
2.2 初始中心优化选取

由于样本分布存在不确定性，传统K＿means算法中依靠随机选取产生的初始聚类中心，有可能是一些孤立点或噪声点。这将导致聚类结果偏离真实分布，从而得到错误的聚类结果，并且这一现象在小样本条件下的发动机状态评估过程中将更加严重。因此本文中提出最小方差启发式初始聚类中心优化选取方法。

该方法的基本思想是:以样本方差作为启发信息，选取方差最小的样本作为初始聚类中心，并以样本平均距离划分初始聚类，从而选择出周围样本分布比较密集的初始聚类中心，避免孤点和噪声点的干扰。算法流程如图2所示。

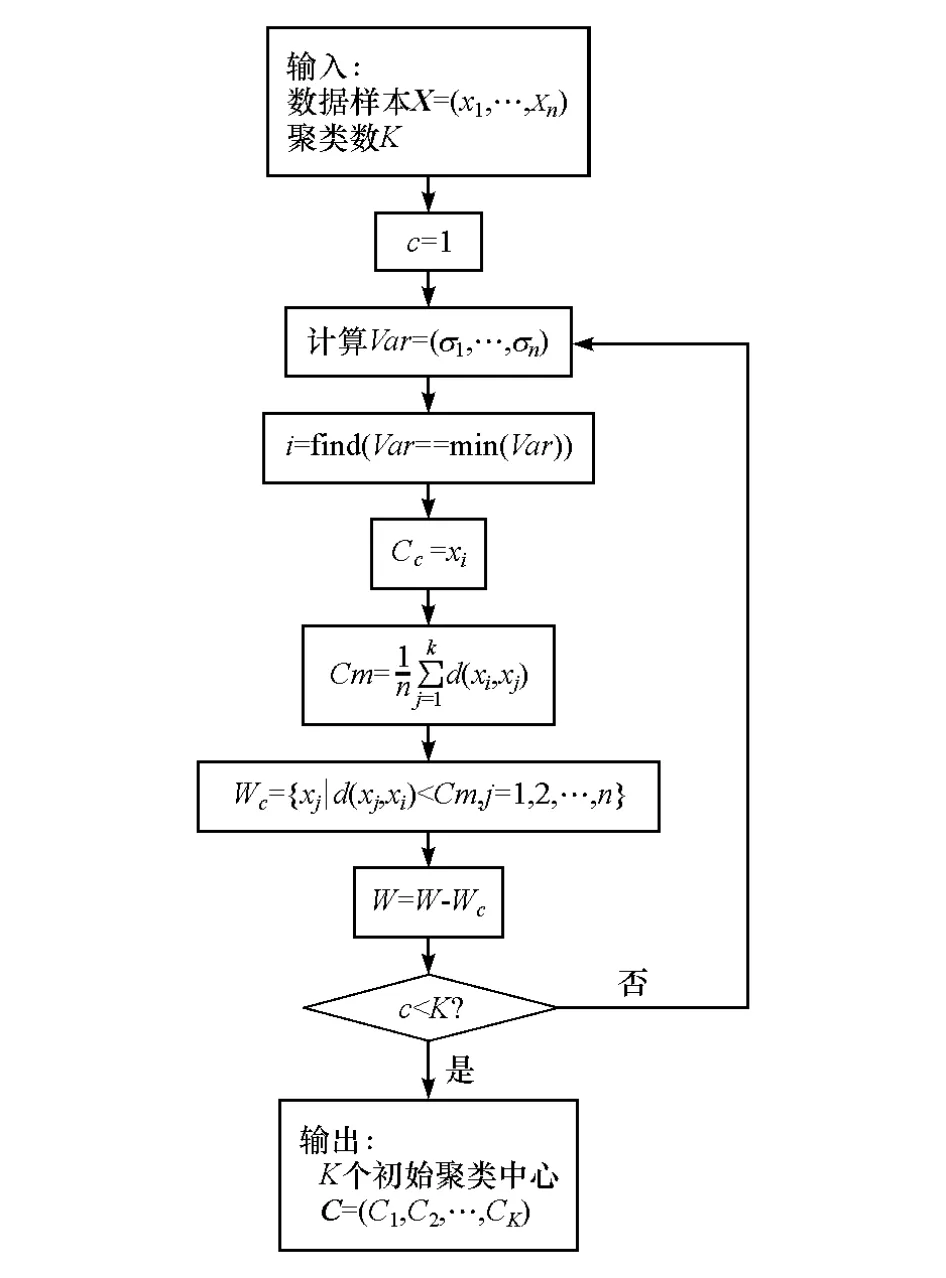
图2 初始聚类中心计算方法

2.3 Bootstrap小子样统计方法

Bootstrap小子样统计方法是一种自助估计方法，其思路是用现有的资料去模仿未知的分布，通过再生抽样将小样本问题转化成大样本，因此该方法适用于小样本条件下的统计推断。

Bootstrap方法基本原理主要根据观测到来自于未知总体分布F的随机子样X＝(X1，…，Xn)，估计总体分布F的某一分布特征R(X，F)，如均值、方差等，从而推测总体分布F，具体方法如下。

设总体分布F的某个分布特征θ＝θ(F)(如均值，方差等)，由观测子样 X＝(X1，…，Xn)构造经验分布 Fn，则有对 θ的估计 θ＾＝θ＾(Fn)，估计误差为

根据经验分布 Fn，重新抽取再生子样X(1)＝(X(11)，…，X(n1))，进而构造经验分布函数F(n1)。于是由X(1)又可得到θ的估计F(n1))。此时可得到估计误差Tn的Bootstrap统计量R(n1)，即

重复抽取多组再生子样 X(i)，i＝ 1，2，…，m，可计算相应的R(ni)，i＝ 1，2，…，m，进而可利用 R(ni)的分布去逼近Tn的分布，即可根据式(1)得到θ(F)的样本:

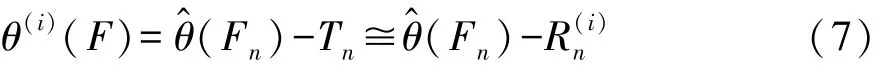
在小样本估计中，该方法较传统统计方法具有较高精度。

3 发动机状态评估实例

3.1 评估样本数据采集整理

以某型装甲车辆柴油机为研究对象，其常用的技术状况评估指标体系如图3所示[7]。对累计使用时间在0～550摩托小时内的发动机，尽量按每间隔50摩托小时选择1台作为基准样本，同时选取3台状态已知的发动机作为测试样本，以验证方法的有效性。采集处理后部分样本状态参数如表1和表2所示。

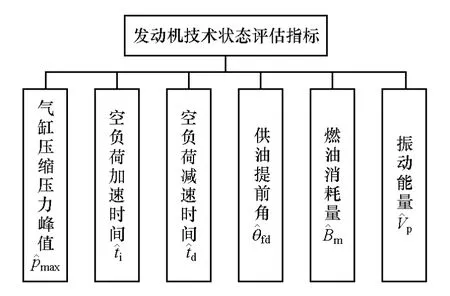
图3 某型装甲车辆柴油机评估指标体系

表1 基准样本状态参数

表2 测试样本状态参数

3.2 发动机状态评估步骤

(1)评估数据选取

在实例验证中，表1样本为基准样本，建立发动机状态评估模型，划分各技术状况等级基准；选取表2样本为测试样本，利用上述模型评估其技术状况，以验证该方法的有效性。

(2)确定评语集

根据柴油机技术状况的优劣程度，建立5级评语集。 将柴油机划分为“好”、“较好”、“一般”、“较差”和“差”5个技术状况等级。

(3)计算各属性权重

根据表1所示样本数据，计算特征参数对应的变异系数:

V＝[0.116，0.482，0.353，0.280，0.724，0.687]

由式(3)可得各属性权重:

W＝[0.044，0.182，0.134，0.106，0.274，0.260]

(4)初始聚类中心

对于发动机而言，由于出厂后需要经历一定时间的磨合，磨合期结束后发动机状态达到最佳，发动机达到规定使用时长的极限，返厂大修时，其状态为最差。因此在采用K＿means聚类算法时，可直接采用磨合期结束时(约50摩托小时)和返厂大修规定摩托小时(约550摩托小时)的样本数据xi和xj分别作为“好”和“差”两个等级的初始聚类中心，并根据其他样本数据，采用图1所示算法流程，计算“较好”、“一般”和“较差”3个技术状况等级的初始聚类中心。

(5)分配样本、更新聚类中心

将测试样本依据式(4)分配到距离最近初始聚类中心相应的簇类中，并根据图2的流程，重新计算聚类中心。更新后聚类中心矩阵为

(6)聚类中心修正

根据原样本分布，重新抽取N组再生子样X(n)，n＝1，2，…，N。 并对再生子样重复步骤(4)和步骤(5)，计算相应聚类中心根据式(6)可知原样本聚类中心的估计误差分布为

本文中取N＝50重新抽取再生子样，依照上述方法估计测试样本聚类中心的误差分布矩阵:

依据Bootstrap小子样统计方法，可利用再生子样修正原样本各技术状况等级的聚类中心:

根据式(9)可得修正后聚类中心:

(7)样本状态评估

利用权重向量V和聚类中心C，根据相似性原理评估13～15号样本的技术状况，测试样本对各等级基准的相似度和评语如表3所示。

表3 测试样本评估结果

测试样本的评估结果能够定量、定性地反映发动机技术状况，并且与发动机实际状况一致，因此该方法可作为在缺少先验知识和小样本条件下对发动机进行状态评估的有效手段。

4 方法对比分析

为对比本文方法与文献[3]中所述传统方法的客观性和稳定性，在上文1～12号基准样本的基础上，以相同方法重新采集整理一组对比样本，如表4所示。

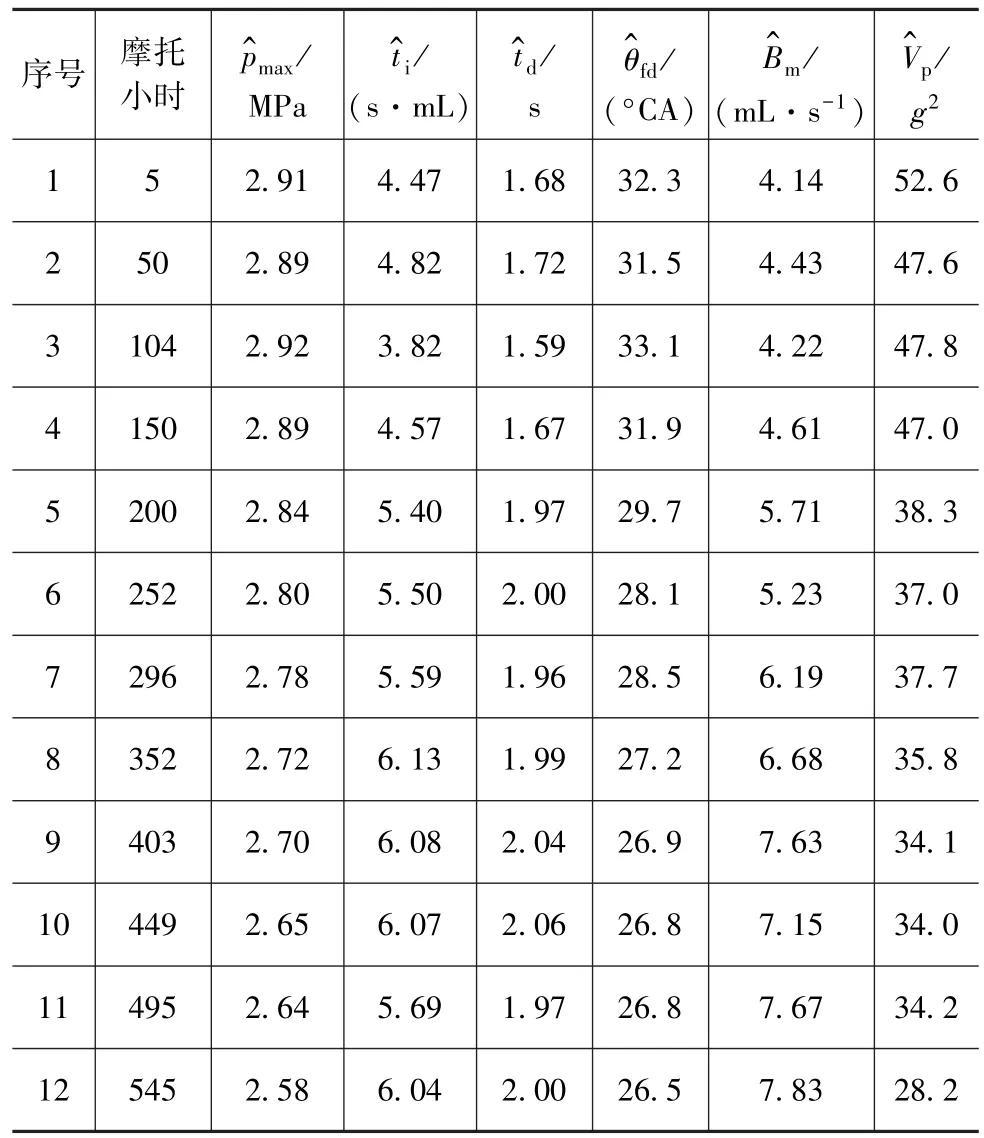
表4 对比分析样本

采用本文提出的基于状态参数方法，分别以第1组和第2组样本建立评估模型，并对所有样本进行评估，结果见图4。

图4 本文方法的评估结果

由图可见:发动机的技术状况随着摩托小时逐渐劣化的趋势明显；在0～200摩托小时内基本为“好”和“较好”，在200～350摩托小时内基本为“较好”和“一般”，在这两个区间内技术状况呈现了两种技术状况变化的过渡，体现了技术状况变化的逐渐性和模糊性；在350～450摩托小时内为“较差”，在500摩托小时以上为“差”。技术状况的这种变化趋势与理论分析的结果大致吻合。

采用文献[3]中所述传统方法，分别以第1组和第2组样本建立评估模型，并对所有样本进行评估，结果见图5。

图5 传统方法的评估结果

用传统方法评估所有27个样本时，有6个样本在两组不同样本建立的评估模型下的结果不同。而本文方法在相同条件下只有2个样本得到了不同结果。这表明本文中提出的基于状态参数发动机状态评估方法在处理少量状态参数样本时比传统方法具有更强的稳定性。

5 结论

本文中利用加权欧氏距离和最小方差启发式算法对K＿means聚类算法进行了改进，并通过融合Bootstrap小子样统计方法提出了一种基于改进K＿means的发动机状态评估方法。

该方法能在缺少先验知识的小样本条件下，建立稳定的发动机状态评估模型，实现发动机技术状况的有效评估。与传统方法相比，该方法在处理随机性较大的状态参数样本时具有更强的稳定性，并且该方法完全依靠发动机状态参数，具有更强的客观性。