表贴式永磁电机磁场的解析计算与分析∗

张河山，邓兆祥，2，杨金歌，妥吉英，张 羽

前言

永磁电机具有高转矩密度、高效率、高功率密度等优点，广泛应用于电动汽车、船舶等工业领域[1]。其结构参数对电机性能影响较大，因此，为设计性能优异的电机需要改变和优化电机结构参数，并采用有限元法或解析法分析其电磁场特性。有限元法可考虑材料非线性影响和分析较复杂结构电机性能，但计算过程耗时、占用资源，且难以对电机特性及其影响因素进行规律性研究，具有明显局限性。电磁场数值解析法计算量较小，物理概念清晰，能清晰反映电机性能与设计参数的关系，适用于电机设计参数优化，因此逐渐引起国内外学者广泛关注。

Bracikowski[2]和Chen[3]等利用集总参数磁路法建立永磁电机电磁场模型，可进行平均磁场分析，计算量小，但无法分析磁场具体分布，计算准确性受模型影响较大。Zhu等[4-5]基于拉普拉斯和泊松方程的磁位解析法对不考虑定子开槽时永磁无刷电机均匀气隙磁场和电枢绕组磁场进行建模与分析。在此基础上，Chen等[6-7]引入相对比磁导函数来修正不考虑定子开槽时光滑气隙磁密，可模拟定子开槽的影响，但无法考虑具体槽型和齿尖对磁场的影响。Zarko等[8-9]将定子槽深假设为无穷大，通过共形映射求解电机气隙相对比磁导函数，可较准确地刻画电机齿槽效应对气隙磁场的影响，但是由于其不能考虑具体槽深对磁场的影响，也不能考虑定子槽间的相互影响，工程应用较少。Zhu等[10]采用傅里叶级数法，将电机求解域划分为多个子域，结合磁场边界条件，将定子槽作为求解域，考虑了定子槽的实际尺寸，计算了永磁电机开路磁场，计算精度较高，但未建立定子槽开口子域模型。郭思源等[11]将子域法应用到外转子游标电机，并考虑了径向、平行和Halbach充磁方式，分别计算了气隙磁密、空载反电势和绕组电感，并通过有限元验证，但也未建立定子槽开口子域模型。Wu等[12-13]在文献[10]的基础上考虑定子齿尖的影响，将定子槽开口作为求解子域，分析了考虑齿尖时永磁电机空载磁场和电枢绕组反应场的分布情况，计算结果与有限元法吻合较好。Liang等[14]利用子域模型法分析轮辐式永磁同步电机，将磁桥作为求解子域，考虑了电枢反应场对磁桥饱和的影响，将子域模型法推广到更实际的工程应用。

在文献[12]和文献[13]的基础上，本文中以一台在定子齿上开有辅助槽的永磁电机作为研究对象，在二维极坐标平面，以矢量磁位为求解变量，在永磁体和定子槽子域建立泊松方程，在气隙、定子槽开口和辅助槽子域建立拉普拉斯方程，通过分离变量法求解各子域矢量磁位通解，根据边界条件和不同子域交界面条件求解各阶次谐波系数。计算电机气隙磁密、空载反电动势、齿槽转矩和电磁转矩等性能，应用有限元验证解析法的准确性。在此基础上，研究了极弧系数、辅助槽尺寸和定子槽开口宽度对电机齿槽转矩和电磁转矩的影响规律。另外，提出一种不等槽开口宽度配合的解析模型，可降低齿槽转矩和电磁转矩脉动。

1 解析计算模型

以内转子表贴式永磁电机进行磁场解析计算，二维极坐标系下结构如图1所示，将整个求解域划分为5类子域:永磁体(子域Ⅰ)、气隙(子域Ⅱ)、定子槽(子域Ⅲ)、槽开口(子域Ⅳ)和辅助槽(子域Ⅴ)。各子域矢量磁位分布的通解可通过求解子域内的拉普拉斯方程或泊松方程得到。为便于数学建模，作如下假设:

(1)忽略端部效应；

(2)永磁体材料去磁曲线为线性；

(3)定、转子铁心材料的磁导率无穷大；

(4)定子槽内线圈边的电流密度Ji1和Ji2均匀分布。

磁场分布可用矢量磁位表示:

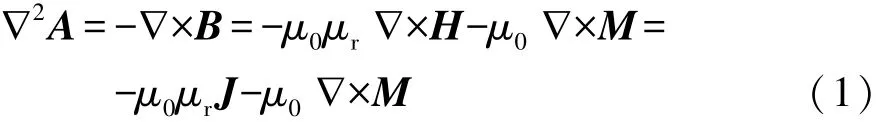
式中:A为矢量磁位；B为磁通密度；H为磁场强度；J为电流密度；M为永磁体剩余磁化强度。

1.1 永磁体子域通解

永磁体子域满足泊松方程[15]为

式中:Mr和Mα分别为永磁体剩余磁化强度的径向和切向分量:

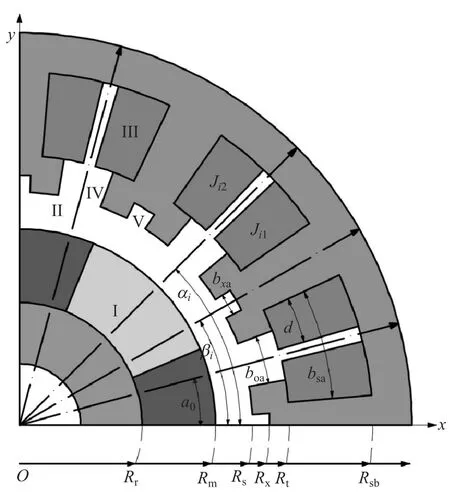
图1 电机几何模型和子域设置

其中

当永磁体径向充磁时[16]:

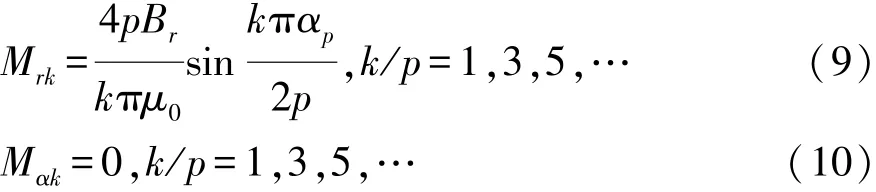
当永磁体平行充磁时:

其中

由于假设定转子铁心磁导率为无穷大，可认为磁力线垂直于铁心表面，所以切向磁感应强度和切向磁场强度皆为零[17]，因此满足边界条件:

由分离变量法可得永磁体子域通解为

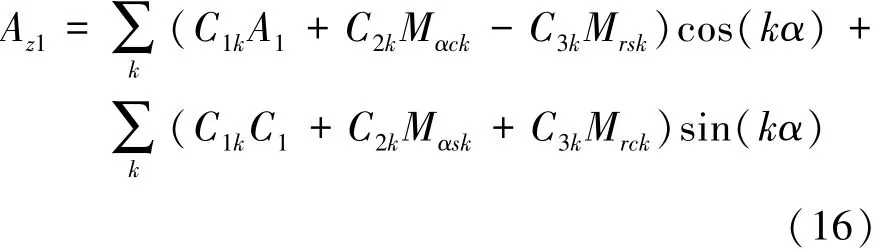
其中

1.2 气隙子域通解

气隙子域满足拉普拉斯方程[18]:

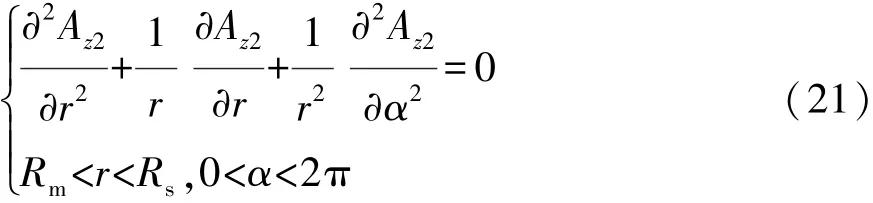
由分离变量法可得气隙子域通解为

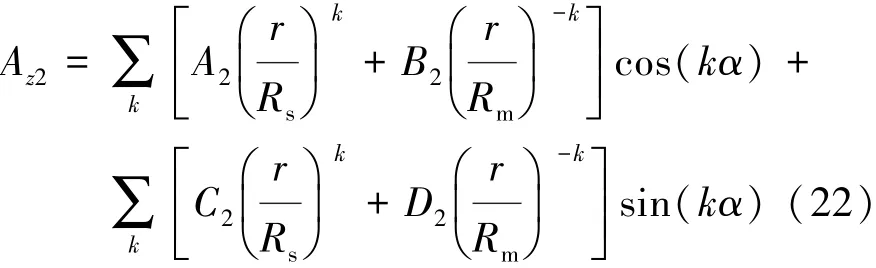
1.3 定子槽子域通解

定子槽子域满足泊松方程:

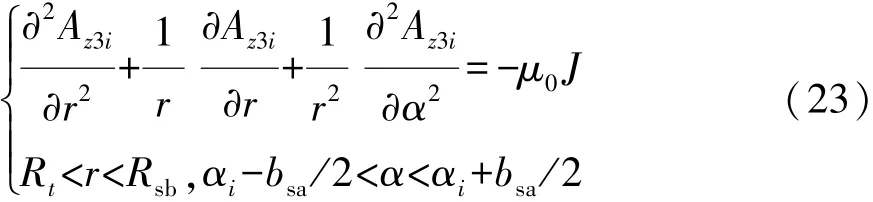
因假设磁力线垂直于铁心表面，故满足边界条件:

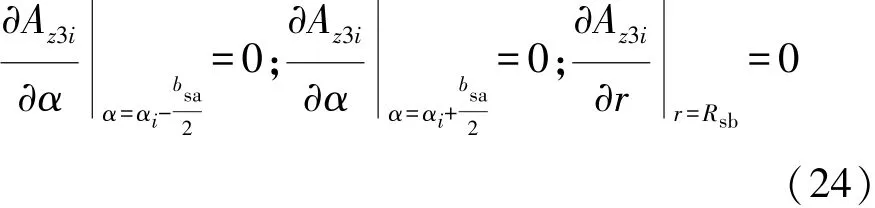
电枢绕组电流密度为

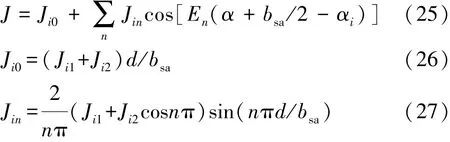
由分离变量法可得定子槽子域通解为

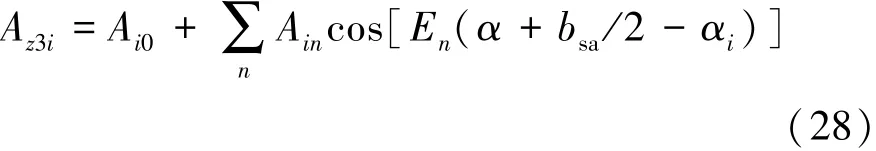
其中

1.4 定子槽开口子域通解

定子槽开口子域满足拉普拉斯方程，即

其边界条件为

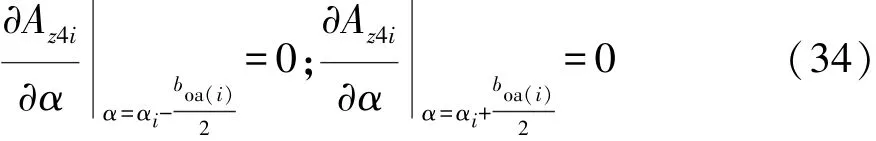
由分离变量法可得槽开口子域通解为

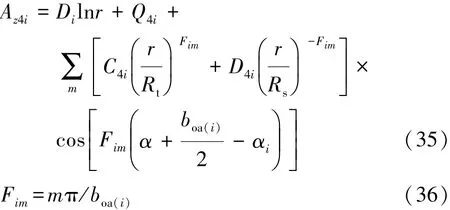
1.5 辅助槽子域通解

辅助槽子域满足拉普拉斯方程:

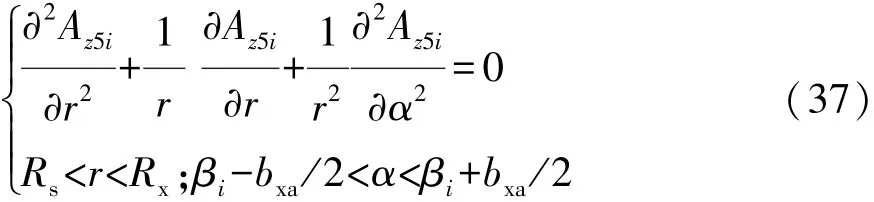
其边界条件为

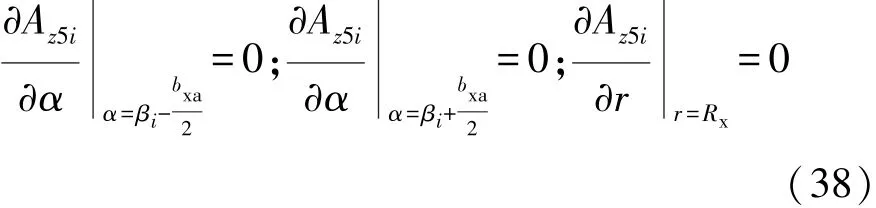
由分离变量法可得辅助槽子域通解为

2 边界条件

在不同子域的交界面法向磁密和切向磁场强度具有连续性，上述各子域通解中的谐波系数可通过建立如下边界条件确定。

(1)在永磁体子域和气隙子域的交界面法向磁密和切向磁场强度相等，可得

(2)在定子槽子域与定子槽开口子域交界面法向磁密和切向磁场强度相等，可得

(3)在气隙子域、定子槽开口子域和辅助槽开口的交界面法向磁通密度和切向磁场强度相等，可得:

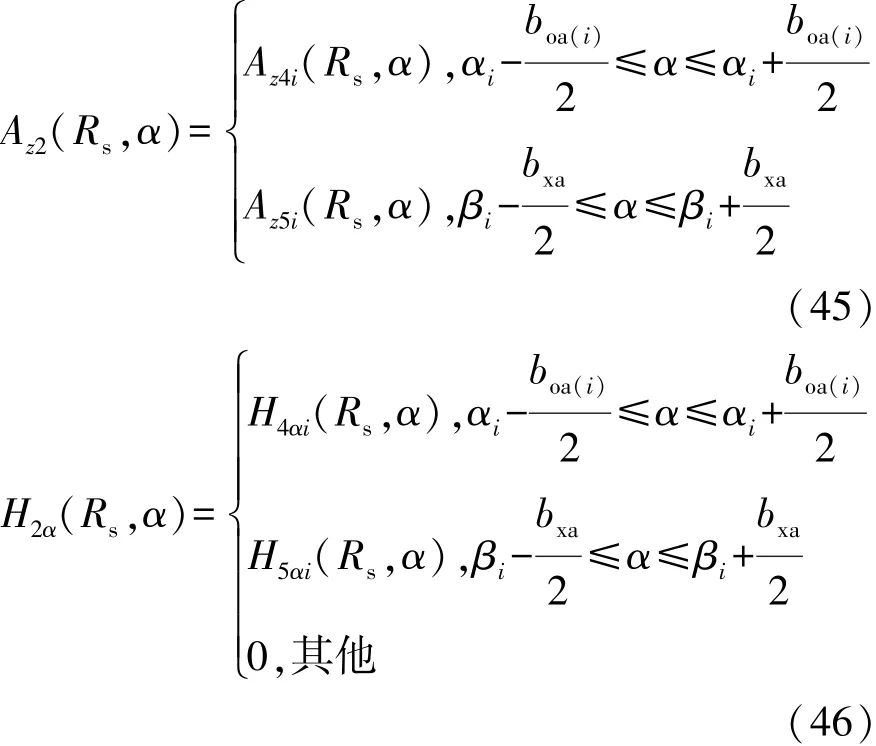
利用式(41)～式(46)求解积分常数，将其改写为矩阵形式，然后联合求解可得到5类子域中各阶次傅里叶级数的系数。

3 电磁性能

电枢槽内左侧线圈边的磁链可通过矢量磁位分布计算:

同理，另外一侧线圈边的磁链为

每个线圈边的面积为

定子槽内绕组布线可通过矩阵表示:

三相磁链为

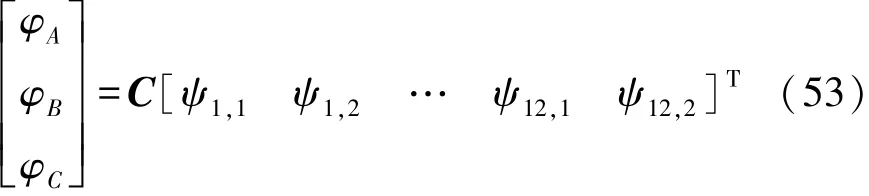
A相反电动势为

齿槽转矩为

电机的电磁转矩为

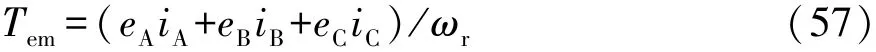
4 磁场计算与有限元验证

以一台8极12槽的永磁电机为例，其主要参数如表1所示。

气隙磁密的径向和切向分量为

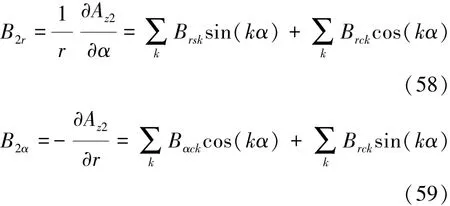
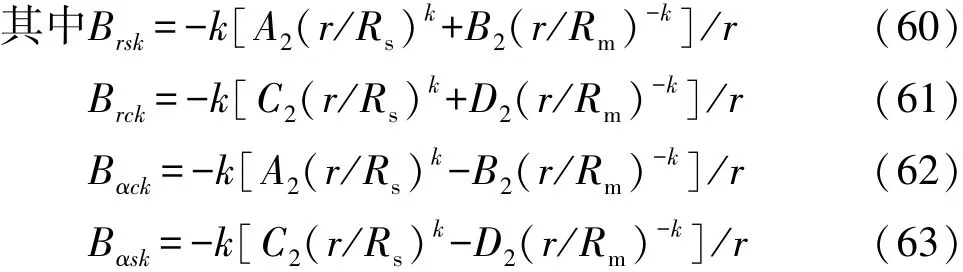
为验证上述理论推导的正确性，分别利用Matlab和Ansoft/Maxwell建立永磁电机磁场模型。图2～图5分别为用解析法和有限元法算得的空载气隙磁密、反电动势、齿槽转矩和电磁转矩。可以看出，解析法与有限元法的计算结果吻合得较好，证明了解析法计算结果是可信的。

表1 电机主要参数

5 电磁特性影响因素研究

在验证解析计算结果正确的基础上，研究了极弧系数、辅助槽宽度与深度和定子槽开口宽度对电机齿槽转矩和电磁转矩的影响。

极弧系数是影响电机的齿槽转矩和电磁转矩的重要因素之一。图6为电机齿槽转矩和电磁转矩随极弧系数的变化曲线。由图6(a)可知，随着极弧系数的增大，齿槽转矩先减小后增大。当极弧系数为0.76时，齿槽转矩最小为0.054 9N·m；当极弧系数为1时，齿槽转矩最大为0.673N·m。由图6(b)可知，随着极弧系数的增大，电磁转矩均值由5.339逐渐增大至6.812N·m，增幅为27.59%。因此在设计极弧系数时应综合考虑，在降低齿槽转矩的同时保持有较大的电磁转矩。

图2 空载径向和切向气隙磁密

图3 空载反电动势

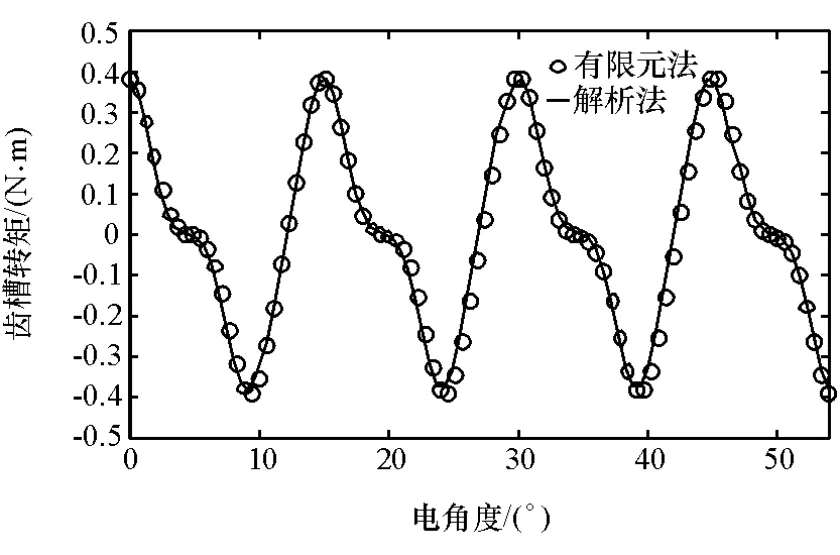
图4 齿槽转矩

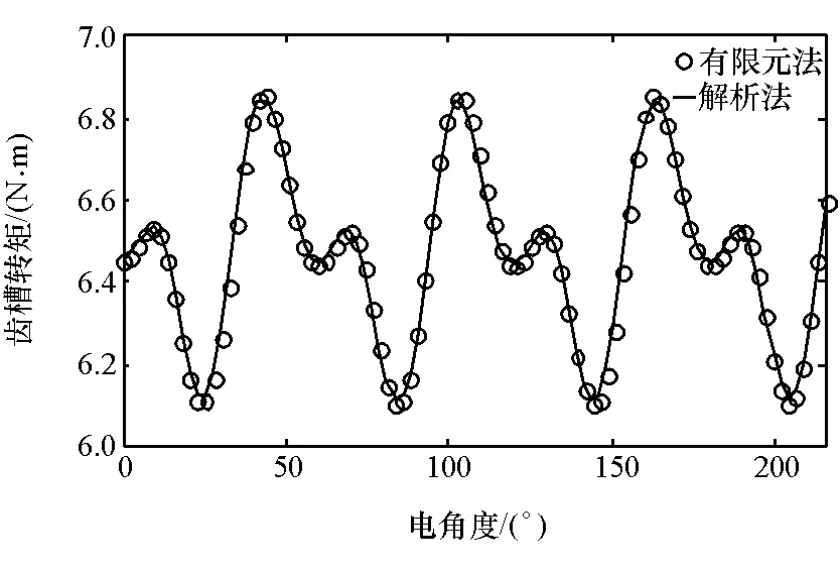
图5 电磁转矩

图6 极弧系数对齿槽转矩和电磁转矩的影响

图7 为电机齿槽转矩和电磁转矩随辅助槽宽度的变化曲线。由图7(a)可知，随着辅助槽宽度增大，齿槽转矩呈现不规则的变化趋势，当辅助槽宽度与定子槽开口宽度比值为1.67时，齿槽转矩最大，为0.884 7N·m；当比值为3.33时，齿槽转矩最小，为0.046 6N·m。由图7(b)可知，随着辅助槽宽度增大，电磁转矩均值由6.514逐渐下降至4.966N·m，降幅为23.76%。因此只有合理选取辅助槽尺寸才能在有效降低齿槽转矩的同时保持较好的电磁转矩特性。

图7 辅助槽宽度对齿槽转矩和电磁转矩的影响

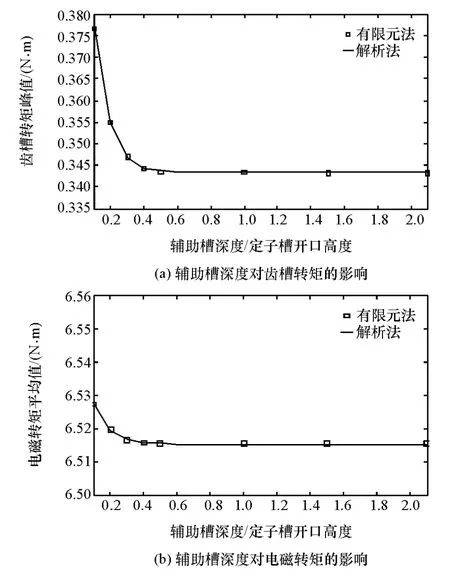
图8 辅助槽深度对齿槽转矩和电磁转矩的影响

图8 为电机齿槽转矩和电磁转矩随辅助槽深度的变化曲线。由图8(a)可以看出，齿槽转矩随辅助槽深度的增大而减小。当辅助槽深度与定子槽开口高度比值小于0.5时，随着辅助槽深度的增大，齿槽转矩由0.371 5迅速下降至0.343 8N·m，降幅为7.46%；当比值大于0.5后，齿槽转矩基本保持不变。由图8(b)可知，电磁转矩随辅助槽深度的增大而减小。当辅助槽深度与定子槽开口高度比值小于0.5时，随着辅助槽深度的增大，电磁转矩均值由6.527 5下降至6.515N·m，降幅为0.191%，当比值大于0.5后，电磁转矩均值基本保持不变。在实际工程应用中，辅助槽太浅，齿槽转矩削弱不明显，过深则会影响磁场分布和定子机械强度，因此应合理设计辅助槽深度，在有效抑制齿槽转矩的同时保证有较好的电磁转矩特性。

定子槽开口是引起永磁电机气隙磁导变化的一个重要因素，因此定子槽开口宽度大小会对齿槽转矩和电磁转矩产生重要影响。图9为电机齿槽转矩和电磁转矩随定子槽开口宽度的变化曲线。由图9(a)可知，随着槽开口宽度增大，齿槽转矩先增大后减小，当槽开口宽度为 10°时，齿槽转矩最大为0.764 5N·m；当槽开口宽度为20°时，齿槽转矩最小为0.038 9N·m。由图9(b)可知，随着槽开口宽度的增大，电磁转矩均值由6.588 6逐渐降低至5.149N·m，降幅为21.85%。

通常情况下，电枢槽的槽口宽度都相同，根据图9定子槽开口宽度对电机齿槽转矩和电磁转矩的影响情况，提出一种不等槽开口配合的解析模型，以图削弱齿槽转矩和电磁转矩脉动，其电枢槽型示意图见图10。相距两个齿距的两槽的槽口宽度相等，而相邻两槽的槽口宽度不等，满足:

图9 定子槽开口宽度对齿槽转矩和电磁转矩的影响

图10 不等槽开口配合示意图

分别利用 3 种不等槽开口(4°与 18°，4°与 19°，4°与20°)与等槽开口的电机进行对比，研究不等槽开口宽度配合对齿槽转矩和电磁转矩的影响，结果如图11所示。由图11(a)可知，对比等槽口结构，随着不等槽开口宽度从18°增大至20°时，齿槽转矩峰值减小，分别为 0.379 8，0.328 2，0.271 1和0.223 2N·m，说明此方法可有效减小齿槽转矩峰值。由图11(b)可知，随着不等槽开口宽度的增大，电磁转矩减小。电磁转矩脉动分别为0.734 5，0.364 9，0.379 5和0.389N·m。因此采用不等槽口宽度配合还可降低电机电磁转矩脉动，但电磁转矩也相对减小。

图11 不等槽开口宽度对齿槽转矩和电磁转矩的影响

综上所述，改变电机尺寸和参数，采用不等槽开口宽度配合可有效减小齿槽转矩，但同时也会减小电磁转矩。在电机设计过程中，应该综合考虑电机电气性能、冲模制造、定子机械强度和下线工艺等因素，合理确定电机尺寸和参数。

6 结论

基于傅里叶级数法将开有辅助槽的表贴式永磁电机求解域划分为5个不同子域，利用边界条件求解各子域通解表达式，计算了电机空载和负载特性，并通过有限元计算验证了解析模型的准确性。

研究电机齿槽转矩和电磁转矩随极弧系数、辅助槽尺寸、定子槽开口宽度的变化规律，结果表明:通过合理选取设计变量可有效降低齿槽转矩，且保持较好的电磁转矩特性。此外，研究发现，不等槽开口宽配合方式可有效减小齿槽转矩峰值和电磁转矩的脉动。

本研究将定转子硅钢片假设为理想材料，即定转子铁心的磁导率为无穷大，今后将进一步研究铁磁材料特性对电机性能的影响。