增程式电动汽车最优曲线模糊控制策略研究∗

牛继高，牛丹彤，徐春华，裴冯来

前言

增程式电动汽车(extended-range electric vehicle，E-REV)具有多种工作模式，当处于增程模式时，发动机/发电机与动力电池一起驱动车辆行驶，使E-REV成为一个典型的多动力源驱动系统[1-2]。E-REV的能量管理策略是目前的研究热点之一，可分为规则型和智能型两类。前者包括恒温器控制策略[3]、多模式切换控制策略[4]、最优曲线控制策略[5]和功率跟随控制策略等[6]；后者包括模糊逻辑控制策略[7-9]、自适应控制策略[10]和基于神经网络的控制策略等[11]。其中，采用模糊控制策略可较好地实现E-REV增程模式下各动力源的能量分配，同时维持动力电池SOC的平衡。

模糊控制具有抗干扰能力强、鲁棒性好的优点。但由于增程器的日益小型化、驾驶员操作的自主性和车辆行驶工况的随机性，采用单模糊控制器的EREV能量管理策略具有一定的局限性。

本文中针对一款E-REV[12]，首先，根据能量管理的控制目标，对E-REV最优曲线模糊逻辑能量管理策略进行分析；其次，利用Simulink和Cruise软件，对基于单模糊控制器的E-REV最优曲线模糊控制策略进行离线仿真，并针对单模糊控制器的不足，设计了发动机工作区间调整模糊控制器，实现多变工况条件下发动机最大输出功率的自适应调整，以提高E-REV的燃油经济性；最后，利用dSPACE公司的软硬件设备和真实控制器(vehicle control unit，VCU)，开展E-REV最优曲线模糊控制策略的硬件在环仿真，以验证E-REV双模糊控制器在实时状态下的控制效果。

1 E-REV最优曲线模糊控制策略

根据E-REV具有全电力驱动能力的特点，为充分利用外电网充入的电能和便于下一次外接充电，要求动力电池有电时(即电池SOC为0.3～0.9)，EREV以纯电动模式行驶；当电池SOC下降到0.3以下时，E-REV进入增程模式。在增程模式下，为保证电池的性能与使用安全和便于外接充电，控制策略须将电池SOC维持在一个适当的范围内。因此，设计最优曲线模糊控制策略的主要目的是为了使车辆在行驶过程中能够根据工况、负荷、动力电池电量等因素实时调整发动机和电池的动力分配，达到整车设计指标的要求，并尽可能地提高燃油经济性。

综上所述，采用最优曲线模糊控制策略对EREV在增程模式下各动力源的能量进行分配，控制目标主要包括两个方面:第一，控制电池SOC在目标值附近，且波动尽可能小；第二，较低的燃油消耗。根据此目标，建立的E-REV最优曲线模糊控制能量管理器如图1所示。

图1中:Pcyc＿ave为车辆需求功率的平均值，包含行驶工况以及车辆本身等多方面的信息，并随着车辆行驶时间的变化而变化；Pice＿max为发动机允许的最大输出功率；ΔPdemand为车辆需求功率的增量；ΔPice为发动机输出功率增量；λ为发动机输出功率增量的修正系数；Pice＿pre为上一时刻发动机的输出功率；Pice＿req为发动机目标功率；Pice＿min为发动机允许的最小输出功率。

图1 E-REV最优曲线模糊控制能量管理器

由图1可以看出，模糊控制能量管理器包含了两个模糊控制模块，即模糊串联功率分配和模糊发动机工作区间调整。前者根据车辆需求功率增量和电池SOC，通过调整发动机的工作点达到驱动功率分配的目的；后者根据行驶工况和电池SOC的实时信息，沿发动机最优曲线自适应地调整发动机的最大输出功率。

2 模糊串联功率分配

串联功率分配控制器(series power distribution controller，SPDC)的设计主要包括以下几个方面的内容:模糊控制器输入量的确定与计算、模糊变量隶属度函数和模糊控制规则的确定以及模糊控制器输出控制变量的求取。

2.1 SPDC输入量的确定和计算

根据加速踏板信号、电机转速和电机外特性转矩，计算电机输出端的目标转矩:

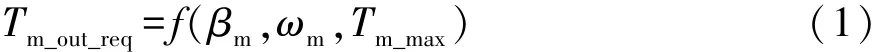
式中:βm为加速踏板信号；ωm为电机角速度，rad/s；Tm＿max为电机外特性转矩，N·m。

根据电机转速、效率和输出端的目标转矩，计算电机输入端的需求功率:

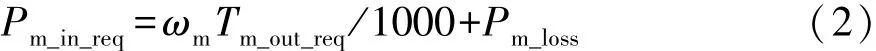
式中 Pm＿loss为电机功率损失，kW。

根据车辆电气附件消耗的功率和电机输入端的需求功率，得到整车需求功率Pdemand:

式中Paux为车辆电气附件消耗的功率，kW。

整车需求功率的增量ΔPdemand为

式中Pdemand＿pre为上一时刻的整车需求功率，kW。

根据仿真分析，确定ΔPdemand的取值范围为[-4，4]kW；增程模式下电池SOC的工作范围为[0.25，0.35]，电池SOC的控制目标值为0.3；由于参数λ的引入，可方便地实现对ΔPice的修正，因此ΔPice的取值范围可依据模糊子集个数和作图的方便进行选取，ΔPice的取值范围定为[-4，4]kW。

2.2 SPDC隶属度函数和模糊控制规则

SPDC的输入、输出语言变量均采用了三角形的隶属函数，该隶属函数运算简单且容易实现，占用的存储空间较少，有利于提高仿真速度，并能满足控制精度的要求。SPDC输入、输出变量的模糊集合规定如下。

动力电池SOC包含5个模糊子集，模糊集合为:{NB，N，ZO，P，PB}；ΔPdemand包含 5 个模糊子集，模糊集合为:{NB，N，ZO，P，PB}；ΔPice包含 7 个模糊子集，模糊集合为:{NB，NM，NS，ZO，PS，PM，PB}。其中，NB表示负大，N表示负，ZO表示零，P表示正，PB表示正大，NM表示负中，NS表示负小，PS表示正小，PM表示正中。根据上述规定，输入变量和输出变量的隶属度函数设计和模糊子集的分布如图2所示。

图2 输入变量和输出变量的隶属度函数

从图2可以看出，输入变量和输出变量的模糊子集在论域上的分布是不均匀的。不均匀分布中“零点”左右的模糊子集划分的较细，每个模糊子集占用的论域区段较小，远离“零点”的模糊子集，其划分则正好相反。因零点对应于控制系统的工作点，故采用这种不均匀分布可使控制器在零点附近的控制动作精确而细腻。

模糊控制规则是模糊控制器的核心，E-REV串联功率分配模糊控制规则的设计原则是在满足路况功率需求的前提下，使电池SOC恒维持在0.3。当整车需求功率基本保持不变，即ΔPdemand为ZO时，如果此时电池SOC为NB，因电池SOC远小于目标值，故发动机除要满足车辆的需求功率外，还须对动力电池充电，此时应对发动机发出功率增加命令，即发动机功率增量ΔPice应取PM；如果此时的电池SOC为ZO，即在目标值附近，发动机只需维持上一步的输出功率即可，即ΔPice应取ZO；而如果此时的电池SOC为PB，应对发动机发出一个负方向的较大的功率增量命令，即ΔPice应取NM。上述控制规则与人对系统的控制过程相似，以此类推，可建立输入变量在其他状态时的控制规则，见表1。

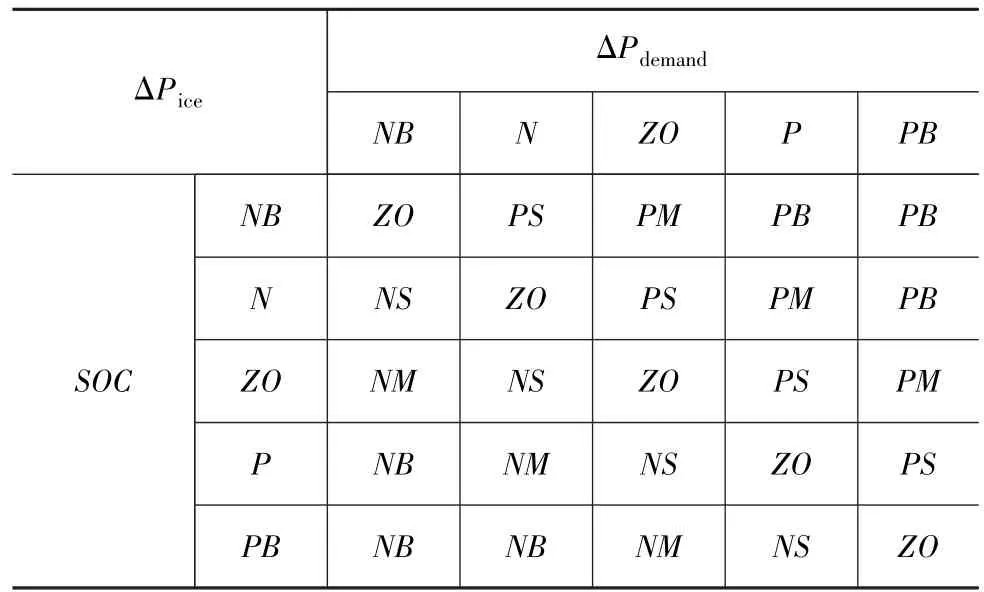
表1 串联功率分配模糊控制规则

根据表1可建立SPDC的规则库，规则库中共包含了25条规则，涵盖了整个输入空间。在模糊运算过程中，采用了Mamdani型(max-min)模糊推理，即蕴含运算采用最小值法min，合成运算采用最大值法max，and运算采用最小算子。

2.3 SPDC的输出控制变量

为在解模糊化时不丢失信息，避免控制量发生跃变，文中采用质心法进行解模糊运算以求取模糊控制器输出控制变量，并根据SPDC的输出ΔPice、修正系数λ和上一时刻发动机的输出功率Pice＿pre计算当前时刻发动机的目标功率Pice＿req:

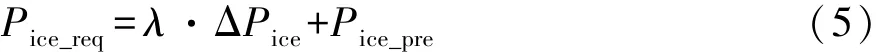
为验证所建立的串联功率分配模糊控制模型的合理性和可行性，将其嵌入到E-REV整车前向仿真模型中，利用典型工况进行仿真计算。图 3为FTP72城市循环工况下工况车速和仿真车速、电池SOC、发动机输出功率的仿真结果。其中，电池SOC初值取 30%，修正系数 λ 取 0.5，Pice＿min取 3.0kW，Pice＿max取 20kW。

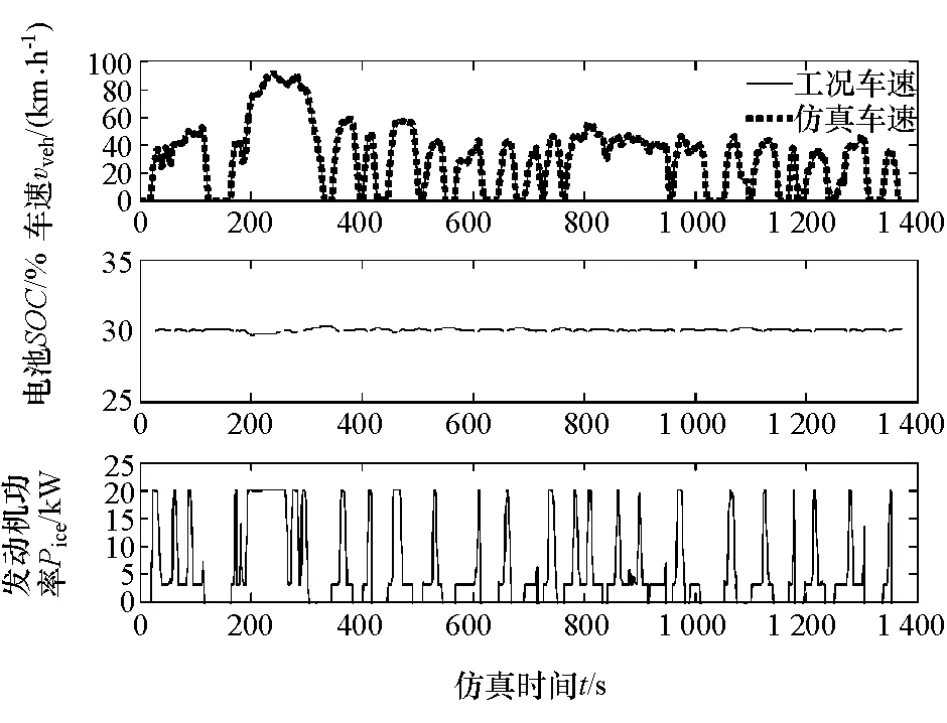
图3 FTP72工况下单模糊控制器仿真结果

从图3可以看出，电池SOC在30%附近波动，幅度变化较小且比较平滑。串联功率分配模糊控制策略在FTP72循环工况下的SOC平衡油耗为6.88L/100km。图4为25kW发动机效率MAP图和最优曲线。由图可见，发动机起动后工作在20kW(B点)附近的时间较长。因此，采用串联功率分配模糊控制策略虽然较好地实现了电池SOC的控制，但却导致了车辆燃油经济性的下降。

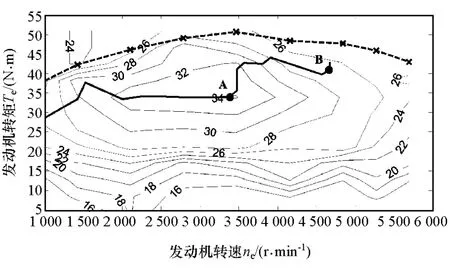
图4 25kW发动机的效率MAP图及最优曲线

在模糊串联功率分配控制策略中有λ，Pice＿min和Pice＿max3个关键参数。其中λ对SPDC输出的ΔPice进行修正，Pice＿min和 Pice＿max决定发动机最优曲线的工作区间。为分析以上参数对电池SOC终值和车辆燃油经济性的影响，仍采用整车模型进行FTP72工况下的仿真计算。表2给出了λ变化时，电池SOC终值和等效油耗的变化情况。其中，SOC初值为30%，Pice＿min和 Pice＿max分别取 3 和 20kW。

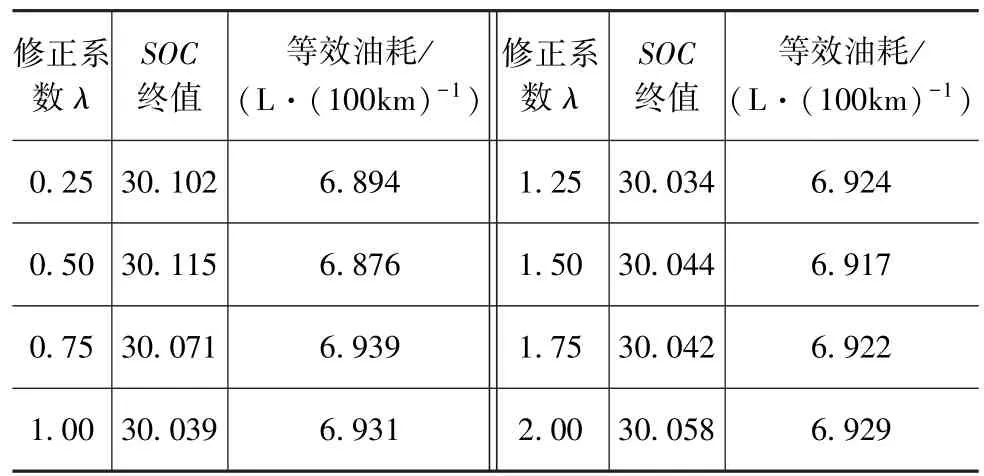
表2 修正系数λ对SOC终值和等效油耗的影响

从表 2可以看出，当修正系数 λ的取值从0.25～2.0变化时，电池SOC终值和车辆的等效燃油消耗基本保持不变。表3给出了当Pice＿max从11～20kW变化时，电池SOC终值和等效油耗的变化情况。 其中，SOC 初值为 30%，λ 取 0.5，Pice＿min取3kW。从表3可以看出，当Pice＿max从11kW开始增加时，电池 SOC终值的变化幅度很小；除 Pice＿max取11kW时的情况外，E-REV的100km油耗随着Pice＿max的增大而增大。产生这种情况的原因在于沿发动机最优曲线，发动机最高效率点所对应的输出功率为11.8kW，随着发动机输出功率的升高或降低，发动机效率皆下降。

根据仿真结果，发动机最小功率Pice＿min对电池SOC终值和等效燃油消耗的影响与λ类似。但选择较大的Pice＿min将导致SOC在目标值附近的振荡加剧，同时也易造成模糊控制策略失去对电池SOC的调节作用。因此，Pice＿min通常取定值，并将其限制在一定的范围内。

由以上分析可知，串联功率分配控制策略的3个关键参数中，Pice＿max是影响车辆燃油经济性的主要因素。根据设计指标，增程模式时要求E-REV能在FTP72，NEDC和 HWFET等工况下行驶，且能以100km/h的巡航车速持续行驶。对应不同的循环工况应适时调整Pice＿max的大小，以满足不同工况时对发动机的功率需求。Pice＿max的调整方式有以下3种:(1)设置为定值，例如将Pice＿max设置为20kW，则能满足上述各工况的功率需求，但会造成 FTP72和NEDC等低速工况下的燃油经济性下降；(2)手动方式，将Pice＿max分为低、中、高3挡，根据经验或车辆行驶情况，由驾驶员手动选择 Pice＿max，但在实际应用中，由于Pice＿max分挡的限制以及行驶工况的不确定性，由驾驶员主导的手动方式存在较大的操作误差，不能保证车辆的燃油经济性最优，且易加重驾驶员的操作负担；(3)自动方式，如图1所示，本文中拟采用模糊控制的方法沿发动机最优曲线自适应调整Pice＿max的大小。

3 模糊发动机工作区间调整

发动机工作区间调整控制器(engine operation region adjustment controller，EORAC)的设计主要包括输入量的确定与计算和模糊变量隶属度函数与模糊控制规则的确定。

3.1 EORAC输入量的确定与计算

根据整车需求功率 Pdemand和工况时间计算Pcyc＿ave，即

式中:Pdemand(t)为整车需求功率，可根据式(3)计算；t为工况时间；t0为t时刻之前车速等于零所占用的时间之和。

由式(6)可以看出，Pcyc＿ave具有以下特点:(1)Pcyc＿ave为变量，随整车需求功率和工况时间的变化而变化；(2)包含了行驶工况和车辆自身的实时信息；(3)考虑了车辆实际行驶过程中临时停车的情况，比式(6)分母中仅取t时，更能反映实际车辆的平均功率需求。

3.2 EORAC隶属度函数和模糊控制规则

EORAC的输入、输出变量采用以三角形为主的隶属函数，输入、输出变量的模糊集合规定如下:SOC包含4个模糊子集，模糊集合为{NB，N，M，P}；Pcyc＿ave包含 9 个模糊子集，模糊集合为{A，B，C，D，E，F，G，H，I}；Pice＿max包含 9 个模糊子集，模糊集合为{A，B，C，D，E，F，G，H，I}。 其中，NB 表示负大，N 表示负，M表示中，P表示正。根据上述规定，输入、输出变量的隶属度函数设计和模糊子集的分布如图5所示。

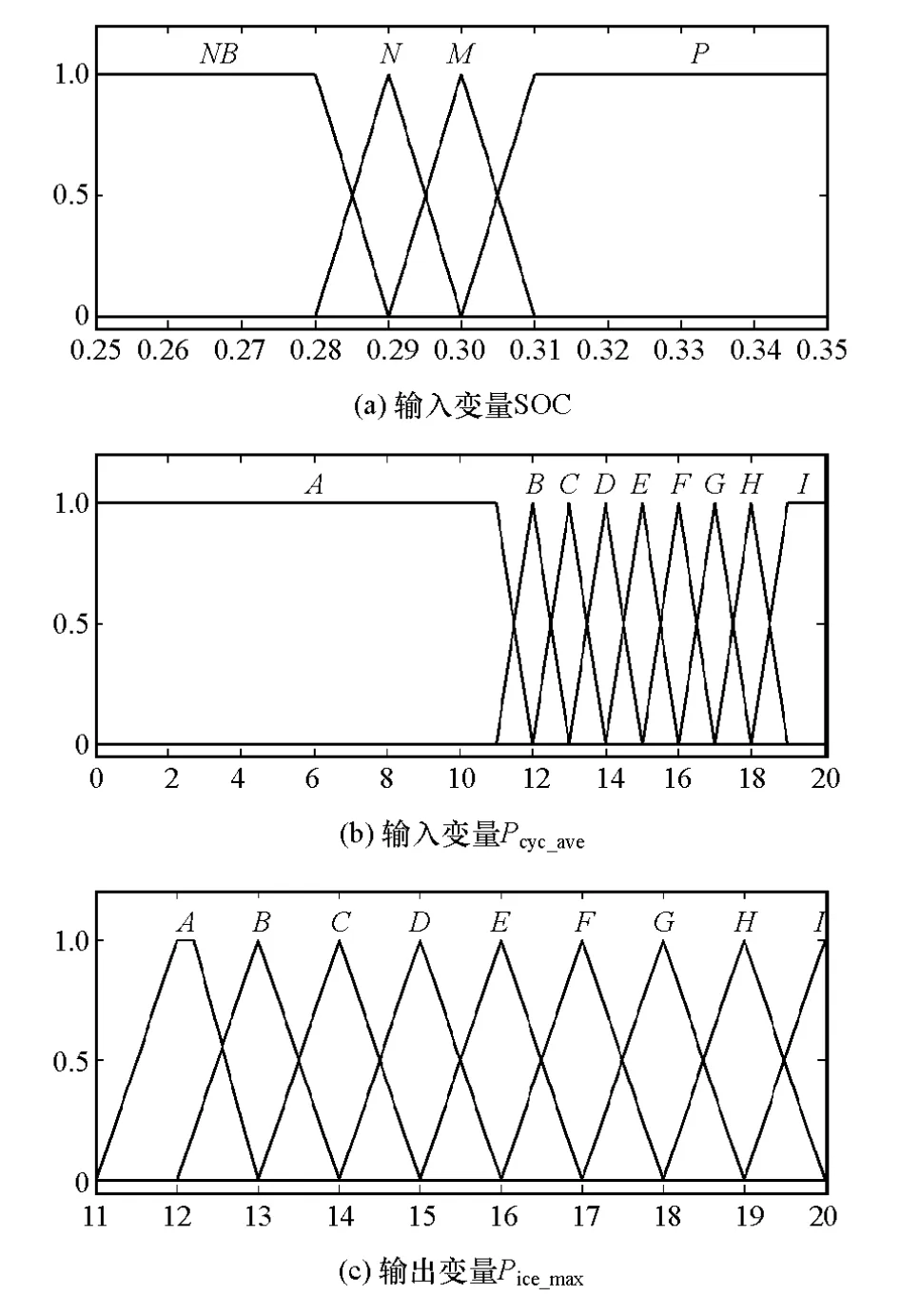
图5 发动机工作区间调整模糊逻辑隶属度函数

当车辆的平均需求功率Pcyc＿ave为B时，如果电池SOC为M，Pice＿max的取值除满足车辆需求功率外，还应有一定的功率裕量，故Pice＿max应取B；如果SOC为N或NB，发动机应有多余的功率给动力电池充电，即 Pice＿max应取 C 或 D；若 SOC 为 H，则应减小Pice＿max的取值，即 Pice＿max应取 A。 以此类推，可建立输入变量在其他状态时的控制规则。发动机工作区间调整模糊控制规则见表4。

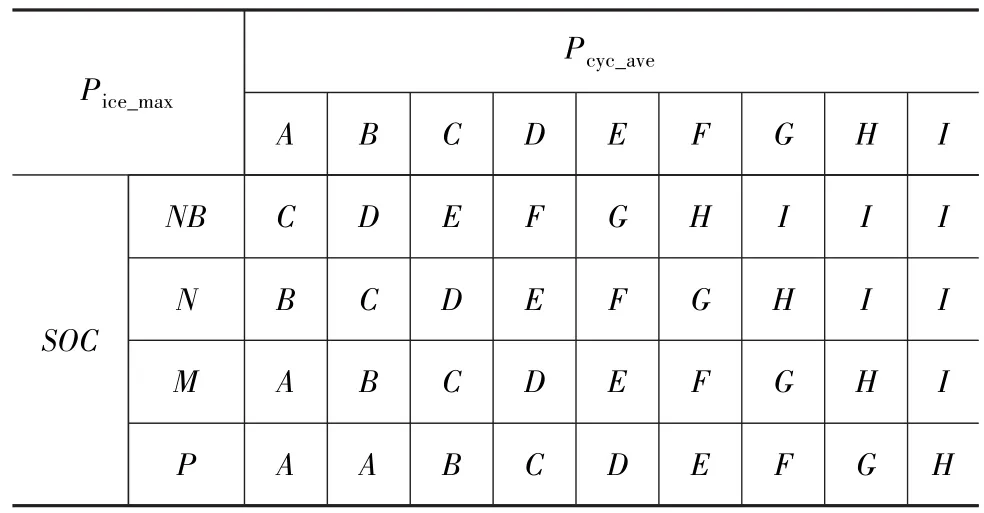
表4 发动机工作区间调整模糊控制规则

与SPDC类似，EORAC的模糊运算采用Mamda-ni型模糊推理，并采用质心法进行解模糊运算。将两个模糊控制器输出的控制变量 Pice＿max和 Pice＿req一起送入发动机/发电机控制模块。

4 硬件在环仿真验证

4.1 硬件在环仿真平台搭建

为验证E-REV模糊逻辑能量管理策略的控制效果，设计开发了整车控制器 VCU实物，使用dSPACE公司的Targetlink自动代码生成工具，完成了模糊控制策略模型转换、在环离线仿真和代码生成，并将生成的代码下载到VCU中。E-REV动力系统等被控对象则采用模型的形式，VCU与被控对象之间通过I/O接口相连。搭建的硬件在环仿真平台如图6所示。

图6 dSPACE硬件在环仿真平台的搭建

上位机PC1完成被控对象的建模、编译和下载，并实现仿真过程的综合管理等功能；模拟器Simulator的主要功能是运行E-REV动力系统仿真模型，并进行模拟器与PC1以及VCU之间的数据交互；上位机PC2完成VCU模糊控制算法的更新、编译和下载，LabVIEW应用程序对VCU运行的关键数据进行在线监控和保存。

4.2 模糊控制算法软件设计

最优曲线模糊控制策略模型主要由整车需求功率计算、再生制动策略、双模糊控制器、车辆需求功率平均值计算和发动机/发电机工作点控制等模块组成。其中，离线仿真过程中，包含了隶属度函数、模糊规则和模糊推理等环节的双模糊控制器是利用模糊逻辑工具箱来完成的，但Targetlink代码自动生成工具并不支持模糊工具箱模块，因此，须对原来的双模糊控制器模块进行转换。本文中采用二维查表的方式实现模糊控制器的功能，图7和图8分别为SPDC和EORAC查表模块所对应的输入/输出曲面图。

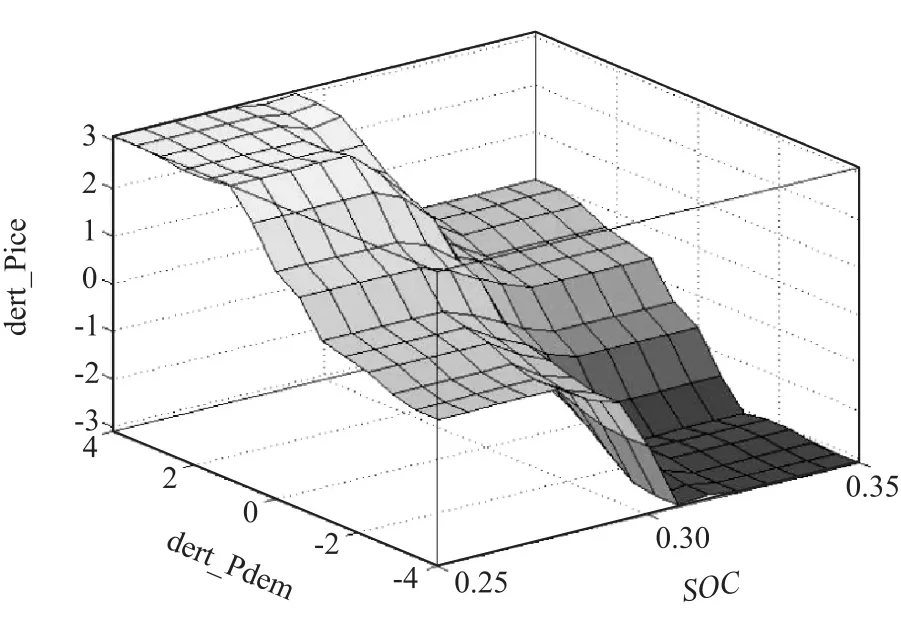
图7 SPDC的输入输出关系(二维查表)

图8 EORAC的输入输出关系(二维查表)

4.3 仿真结果分析

根据电池SOC初值的不同分以下两种情况进行仿真:一是SOC初值取30%，一个行驶工况内车辆始终处于增程模式，有利于考查双模糊控制器对电池SOC的控制效果；二是SOC初值取25%，便于同时考查策略对电池充电过程和SOC平衡过程的综合控制效果。同时为便于仿真结果的对比，所采用的整车配置参数与之前离线仿真模型参数相同。图9和图10分别给出上述两种情况下，选取FTP72循环时E-REV最优曲线模糊控制策略的硬件在环仿真结果。

由图9可知，EORAC根据车辆平均需求功率和电池SOC的大小自适应调整发动机的工作区间，较好地实现了工况始末电池SOC的平衡。与图3相比，图9中发动机起动后工作在12kW(图4中A点)附近的时间较长，与单模糊控制器相比，采用双模糊控制器后的E-REV在FTP72循环工况下的SOC平衡油耗为 5.79L/(100km)，燃油经济性提高了15.8%。

图10 硬件在环仿真结果(SOC初值取25%)

由图10可见，由于电池SOC初始值较低，EORAC的调控作用增强(即图中Pice＿max取值较大，为14kW)，允许发动机输出较大的功率，除满足车辆驱动需求外，富裕部分对动力电池充电。因此，在仿真的初始阶段，电池SOC呈逐渐上升的趋势。当电池SOC上升至目标值附近时，Pice＿max值逐渐降低到发动机高效点，以保证E-REV能够获得较优的燃油经济性。仿真结束时，电池SOC被较好地控制在目标值附近。

NEDC和HWFET循环下的硬件在环仿真结果与FTP72循环类似，不再赘述。

5 结论

针对增程式电动汽车多动力源的能量分配问题，本文中提出一种基于双模糊控制器的E-REV最优曲线模糊控制策略。根据离线硬件在环仿真的结果，可得到以下结论。

(1)对于配置了小功率增程器的E-REV，采用单模糊控制器可较好地实现E-REV增程模式下动力电池SOC的平衡问题；但由于车辆实际行驶工况的不确定性，尤其是在低速工况下，易造成E-REV燃油经济性的下降。

(2)发动机工作区间调整模糊控制器能根据动力电池SOC和车辆行驶工况的实时信息自适应调整发动机最优曲线的工作区间，有利于E-REV中低速工况下燃油经济性的提高。