某姿控发动机组安装板结构拓扑优化设计

2018-08-16冯思锐郑彦博

导弹与航天运载技术 2018年4期

冯思锐，何锋，王浩，刘忠，郑彦博

（1. 贵州大学机械工程学院，贵阳，550025；2. 贵州梅岭电源有限公司，遵义，563000；3. 贵州航天朝阳科技有限责任公司，遵义，563000）

0 引言

对于飞行器而言，结构质量系数（结构质量和飞行质量之比）的高低是体现飞行器结构强度综合技术水平的一项重要指标。在飞行器总体结构设计确定的前提下，对飞行器进行轻量化设计可以有效提高飞行器的结构质量系数。轻量化主要通过结构优化、材料优化和力学性能的提升来实现，材料优化和力学性能的提升均有化学性能的改变，因此结构优化简单、易行。

结构优化主要包括形状优化、尺寸优化和拓扑优化[1]，拓扑优化的不同是在给的设计区域内寻找力的最优传递路径。张伟、侯文彬[2]等采用拓扑优化中的遗传算法对电动汽车进行多目标的拓扑优化计算，提高了车身的设计效率；刘文章等[3]通过拓扑优化分析，改进了某型飞机翼身结合加强框模型，提高了加强框的刚度；马青等[4]通过对圆柱壳体结构进行拓扑优化，使低阶固有频率增加了8.24%，达到了优化目的。

鉴于航天飞行器姿控动力系统结构的刚度和强度要求高，结构质量系数要求低的特性，本文将通过有限元法对某在研新型液体姿控动力系统的发动机组进行拓扑计算，在计算结果的基础上针对原始模型分别进行等质量和等结构优化，为后续的结构改进给出一定的参考。

1 姿控发动机模型

姿控发动机组的数目和布局方式因不同的工作任务有所不同，但国内外一组姿控发动机的数目通常为四、六、八，安装位置有集中和分散 2种，安装角度有“横平竖直”和“倾斜”2种。布局方式一般为四姿控发动机分散倾斜布局[5]、六姿控发动机分散布局[6]、六姿控发动机集中布局[7]和八姿控发动机布局[8]，如图1所示。

图1 姿控发动机布局示意Fig.1 The Position Control Engine Layout

由图1可知，飞行器在工作过程中均可执行俯仰、偏航和滚转任务，而本姿控发动机组仅对飞行器进行俯仰和偏航控制，因此安装角度选择“横平竖直”，因受质量和空间的限制，发动机选为 4台，布局方式为四姿控发动机“十”字布置。其主要包括：发动机安装板、发动机支撑骨架、发动机、电磁阀、管路和控制系统等。

2 建模

2.1 模型的简化

由于液体姿控发动机组系统复杂，工作区间位于0～140 km的大气层内，飞行时间短，受力大，安装支撑板和支撑骨架为主要承受和传递载荷的部件，发动机为载荷的产生部位，电磁阀基本不承受发动机的外力载荷，故将系统的电磁阀、管路、测试口、小的螺钉、螺钉孔、小的倒角等忽略，简化三维模型，简化后的模型如图2所示。因此在符合真实受力情况的前提下减少了计算量。

图2 简化后模型Fig.2 Simplified Model

2.2 模型的建立

2.2.1 材料基本参数

通过ANSYS软件进行计算分析，安装板材料为铝合金6061-T6，主要参数指标如表1所示。

表1 材料基本参数Tab.1 Material Basic Parameters

2.2.2 有限元模型

根据对模型的简化，合并曲率相同的曲面、曲线，在网格划分中选用六面体和四面体网格进行自动划分，建立如图3所示的有限元模型。

图3 有限元边界示意Fig.3 Finite Boundary Indication

2.2.3 边界条件

4台姿控发动机通过螺钉与支撑骨架连接，骨架的上缘与安装板隼焊为一体，安装板通过安装支耳上的8颗螺钉固定到舱体。因此在安装板与舱体连接的螺钉孔处施加固定约束，螺钉头与安装板接触部位限定z轴自由度为0，姿控发动机组工作的最大工况为相邻两台发动机同时工作，每台发动机峰值推力为1600 N，对相邻两台发动机各施加1600 N载荷，飞行器工作中最大加速过载为7.5 g，按照20%的安全余量进行计算，施加加速度为9.0 g，再加上1.0g的自身重力。

2.3 有限元计算

在以上约束加载的基础上对模型进行计算分析。发动机组的应力变化如图4所示，应变变化如图5所示。

图4 应力云图Fig.4 Stress Cloud Map

图5 位移云图Fig.5 Displacement Cloud Map

由图4、图5可以看出，最大应力位于安装板的加强筋和安装板筒体边缘，为91 MPa，最大位移为0.884 mm。当x方向和y方向两台发动机同时工作时，推进剂燃烧产生推力传递给骨架，骨架传递到安装板，安装板产生一个与x轴负方向成45°角的翻转力矩，使安装板形成挤压力，在加强筋和筒体处产生压应力集中，在靠近发动机一侧的筒体处产生沿 z轴负方向的位移，使发动机产生偏斜。

发动机偏斜严重影响飞行器姿态控制的准确性，图5中发动机尾部的位移达到0.884 mm，偏斜过大，考虑到飞行器结构质量系数因素，首先通过拓扑优化计算找到结构中力的传递路径，然后参照拓扑计算结果修改模型，最后将修改后的模型进行有限元计算。

3 优化

ANSYS中的拓扑优化模块采用的是均匀化方法[9]。此算法中，以结构的柔顺性最小（刚度最大）为拓扑优化目标，考虑结构的质量，以材料体积减少和全局最大应力为约束，进行优化计算，则拓扑优化的数学模型为

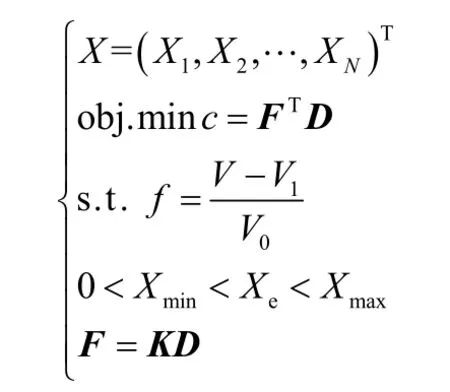
式中 c为结构的柔顺度；F为载荷矢量；K为刚度矩阵；D为位移矢量；V为结构充满材料的体积；V0为结构设计域的体积；V1为单元密度小于 Xmin的材料的体积；f为剩余材料百分比；Xmin为单元相对密度的下限；Xmax为单元密度的上限。

3.1 模型拓扑优化

优化区域为发动机安装支撑板，优化方向为z轴，建立以最大刚度为优化目标，以体积和全局应力为优化的约束条件，定义最大应力为 160 MPa，文献[10]的研究结果表明：在拓扑优化时，体积减少设置为40%～60%可以获得理想的结果，在此设置体积约束为体积减少40%～60%，收敛公差为0.5%。拓扑计算时目标函数-柔顺性的迭代历程如图6所示。

图6 迭代历程曲线Fig.6 Iterative History Curve

从图6中可以看出，迭代5次后结构柔顺性明显降低，迭代次数在50次时结构柔顺性趋于平缓，迭代71次时结果收敛。经过拓扑优化后，得到如图7所示的形状。

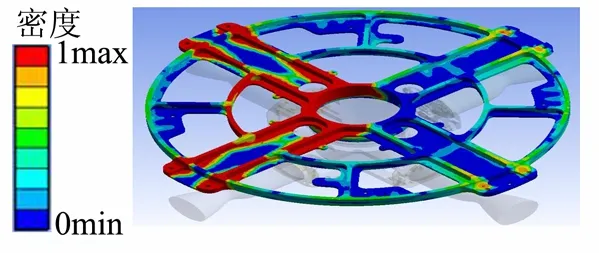
图7 拓扑优化结果云图Fig.7 Topology Optimization Result Cloud Map

图7的左上方为拓扑优化设计伪密度值的对比尺度，密度为 1的位置对应深色区域，即为力的传递路

径，阈值为0.5时的力的传递路径形状如图8所示。

图8 阈值0.5形状Fig.8 Valve 0.5 Shape

由图8可知，安装板结构的主要受力位置为主加强筋和筒体，由于发动机的布置为“十”字布置，此拓扑计算的载荷为相邻两台发动机工作时的状态，因此模型优化的主要部位为图 8中整个安装板主支撑架上深色位置，需增加安装板主加强筋和中间筒体的厚度。

根据拓扑优化结果，在三维建模软件中对模型进行等质量和等刚度修改。

3.2 优化前后对比分析

对修改后模型进行有限元计算时，约束条件、网格划分和载荷施加均同优化前模型一样，再将优化前后模型的有限元计算结果进行对比分析。

3.2.1 有限元静力学计算对比分析

对模型优化更改后，进行有限元计算，将优化前后结构的参数做比较，其结果如表2所示。

表2 结构参数对比Tab.2 Comparison of Structural Parameters

将模型优化前后的质量、刚度和强度进行对比，其结果如表3所示。

表3 优化前后质量、刚度和强度对比Tab.3 Comparison of Quality and Strength before and after Optimization

续表3

由表3可知，等质量和等刚度模型与优化前模型应力集中的位置和位移变化最大的位置基本没变，等质量优化时最大应力减少 44%，刚度提高 21.4%；等刚度设计时安装板质量减少15.3%，应力增加18.7%为108 MPa小于材料的屈服强度276 MPa，结构的安全系数为2.56。

等质量改进时质量没有减少，等刚度改进时刚度没有提高，各有弊端，但这样对比改进得出增加筋的厚度可以改变结构的刚强度。结合等质量和等刚度位移云图发现，在筒体附近加强筋的厚度对刚度影响较大，故将主加强筋从筒体附近向边缘由厚变薄渐变，这种结构和优化前模型比较应力减小 28.1%，刚度提高19.0%，质量减少10.2%。

3.2.2 有限元模态计算对比分析

模态分析主要用于确定结构或机器部件的振动特性，同时也是其他动力学分析的基础[11]。由于计算模型为对称结构，而分块兰索斯法可以很好地求解对称特征问题，因此本文采用分块兰索斯法提取前6阶模态。模型优化前后前6阶固有频率如表4所示。

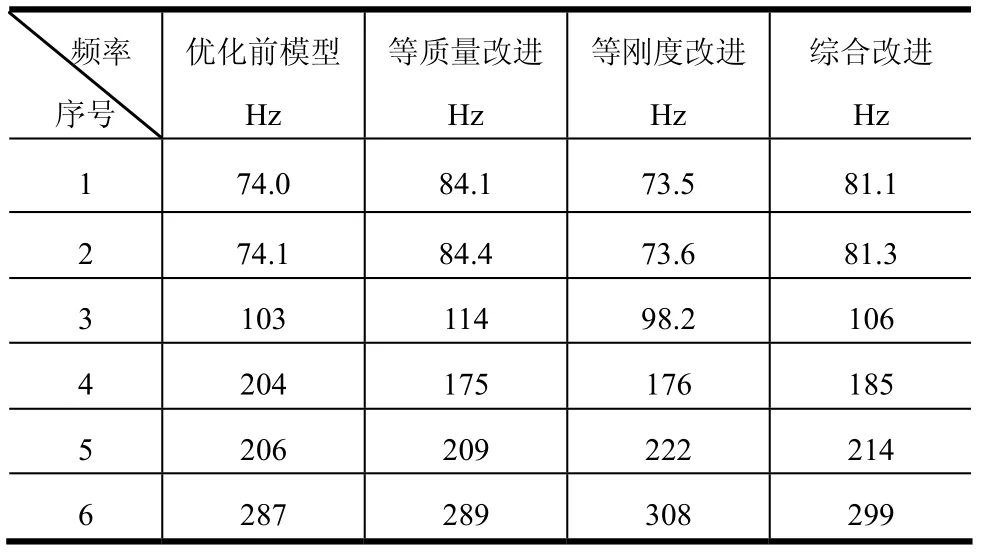
表4 优化前后的前6阶固有频率Tab.4 First 6 Order Natural Frequencies before and after Optimization

从表4中可知，每种模型前两阶固有频率均相差不大，原因为所分析结构是对称结构，将结构每旋转90°后，与原结构位置重合，频率基本一致，阵型相差90°；等质量模型的一阶固有频率为84.4 Hz，比优化前模型一阶固有频率增加 14.1%；等刚度模型一阶固有频率为73.5 Hz，比优化前模型一阶固有频率降低0.6%，综合优化模型一阶固有频率为81.1 Hz，比优化前模型一阶固有频率增加10.3%。

每台发动机的脉冲频率为0～34 Hz，结构易产生共振的频率范围为0～41 Hz，结构低阶固有频率均不在发动机工作的主频范围内。