基于终端速度约束的助推-滑翔飞行器滑翔弹道设计方法

2018-08-16卜奎晨赵长见许泽宇

导弹与航天运载技术 2018年4期

卜奎晨，赵长见，赵洪，高峰，许泽宇

（中国运载火箭技术研究院，北京，100076）

0 引言

助推-滑翔飞行器采用火箭助推，利用滑翔体良好的气动外形，在大气层内超高速飞行，可实现全球快速打击。由于其滑翔飞行弹道位于临近空间，具有较强的机动能力和突防能力，是近年来世界主要军事大国的研究热点。但其助推-滑翔飞行器飞行弹道低、速度快，飞行环境恶劣，导致弹道、控制设计难度较大。

中国在助推-滑翔飞行器领域研究取得了较多的研究成果。在弹道设计方面，雍恩米等[1]针对助推-滑翔式导弹自由飞行段、稠密大气和稀薄大气之间弹道、滑翔弹道的射程近似解开展研究，为射程和峰值热流等特征参数估算提供了依据；杨铮等[2]采用序列二次规划法（Sequential Quadratic Programming，SQP）完成助推-滑翔导弹助推段弹道优化，为获得滑翔段起始点最大动能和实现弹道顺利衔接提供了解决方案；徐申达等[3]针对再入大气层后带动力的跳跃式飞行弹道进行了研究，针对发动机点火次数、点火高度及推力大小的影响开展了分析，得到有益的结果；李瑜等[4]针对SANGER再入-跳跃式弹道[5]、助推-滑翔-弹跳式弹道进行了对比分析，表明再入-跳跃式弹道对提高射程能力更为有利，但会极大提高驻点热流峰值，对热防护不利，而助推-滑翔-弹跳式弹道射程较优，且驻点热流峰值满足约束要求。

目前，中国学者针对助推-滑翔式导弹弹道模式及弹道优化设计方面进行了广泛而深入的研究，但在弹道设计上多是采用优化方法（如SQP等）给出寻优结果，缺乏对鲁棒性较好的滑翔段弹道设计方法进行研究。在实际工程应用中，由于飞行器本身质量特性、发动机性能及气动参数等存在偏差，以及飞行过程中大气干扰的存在，在一定程度上造成滑翔起始点存在位置、速度偏差。此外，实际飞行弹道偏离理想弹道将会导致落地速度存在偏差，需要开展落地速度控制方法研究，从而满足对目标的打击需要。

目前对于无动力滑翔式飞行器的终端位置控制具有较为成熟的方法，而对于速度控制的方法较少。滑翔弹道一般有平衡滑翔和跳跃滑翔两种方式，为研究问题方便，本文针对平衡滑翔弹道，即钱学森式[6]助推滑翔弹道（见图 1）进行研究，给出基于终端速度约束的滑翔弹道设计方法，该方法具有一定鲁棒性，为实现偏差情况下的滑翔弹道和终端速度控制联合设计提供了工具。

图1 “钱学森式”助推滑翔弹道Fig.1 TSIEN H.S.-trajectory for Boost-glide Vehicle

1 滑翔射程及滑翔终端速度计算

对于在大气层内飞行的滑翔式飞行器而言，滑翔飞行弹道影响滑翔终端速度，由于不同滑翔高度的气动阻力不同，在滑翔距离一定的情况下不同滑翔高度对应的滑翔终端速度也不同，二者是紧密耦合的关系。为了实现满足滑翔终端速度约束的滑翔弹道设计，需要解决滑翔射程和滑翔终端速度的快速工程计算问题。

1.1 平衡滑翔射程计算

为了开展平衡滑翔射程快速计算，进行如下简化假设[2]：

a）不考虑地球旋转，即eω=0；

c）滑翔式飞行器无侧滑，即β=0。

在滑翔式飞行器的滑翔轨迹平面内建立发射坐标系 O-xyz和速度坐标系见图2。

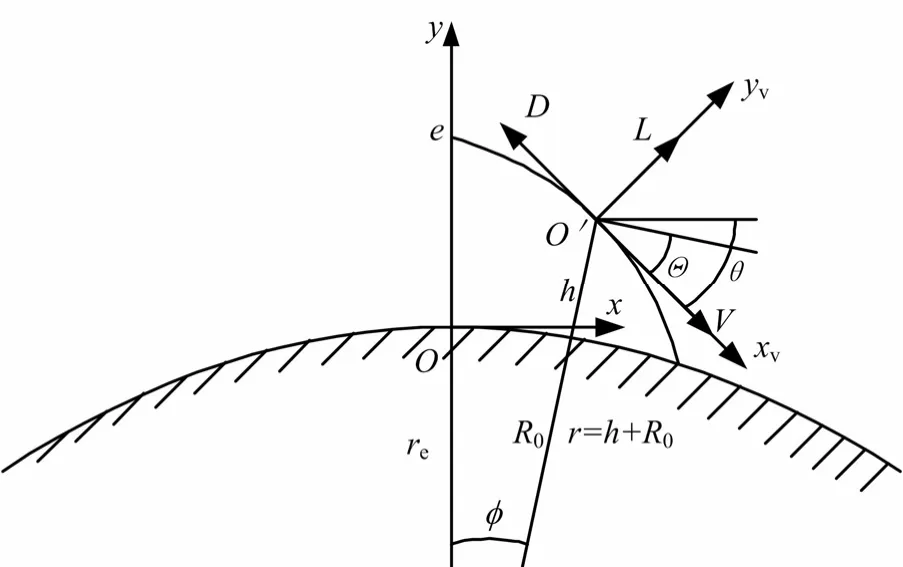
图2 滑翔飞行角度关系示意Fig.2 Angles Relationship of Gliding Flight

在发射坐标系-Oxyz建立运动方程：

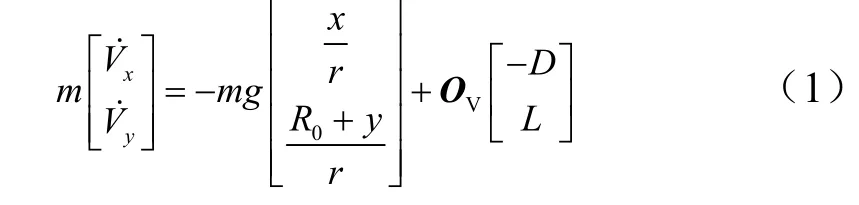
由图2，有：

式中φ为er与r之间的夹角，称为射程角，其中，er为滑翔起点距地心的矢径。

将式（2）、式（3）代入式（1）可得：

进一步转换到速度坐标系，将式（4）两边同乘以矩阵VO的转置矩阵OV，整理得：

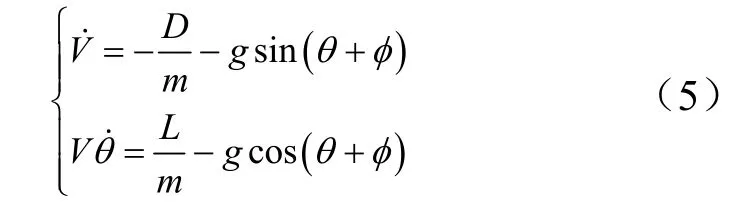
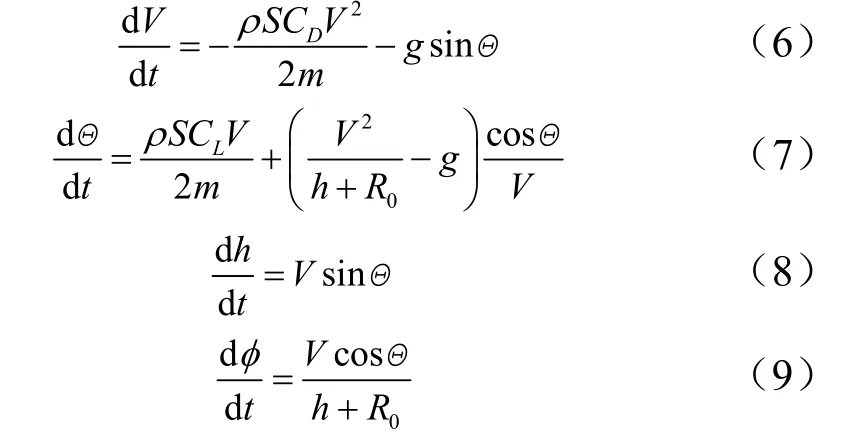
高超声速滑翔式飞行器滑翔距离一般在 1000 km以上，而滑翔段弹道高度变化范围基本在30 km以内，对于钱学森式弹道模式而言，当地弹道倾角及其变化率均很小，可认为0=Θ，0=˙Θ，则由式（9）除以式（6），可得射程角对速度的偏导数：

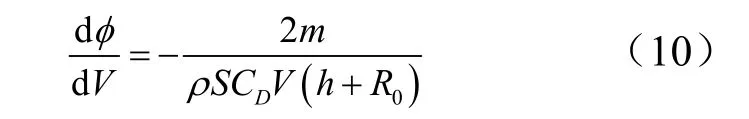
代入式（10），整理可得：

近似认为滑翔弹头在飞行时升阻比K和滑翔高度h保持不变，设0V和0h分别为滑翔起始点的速度和高度，由0=˙Θ知0hh= ，经积分，得到平衡滑翔状态下射程角φ的解析计算公式：

从而可以得到平衡滑翔距离公式为

以 HTV-2[7]为例进行平衡滑翔距离公式验证，弹道仿真结果与采用式（15）进行工程计算结果的对比情况如表1所示。

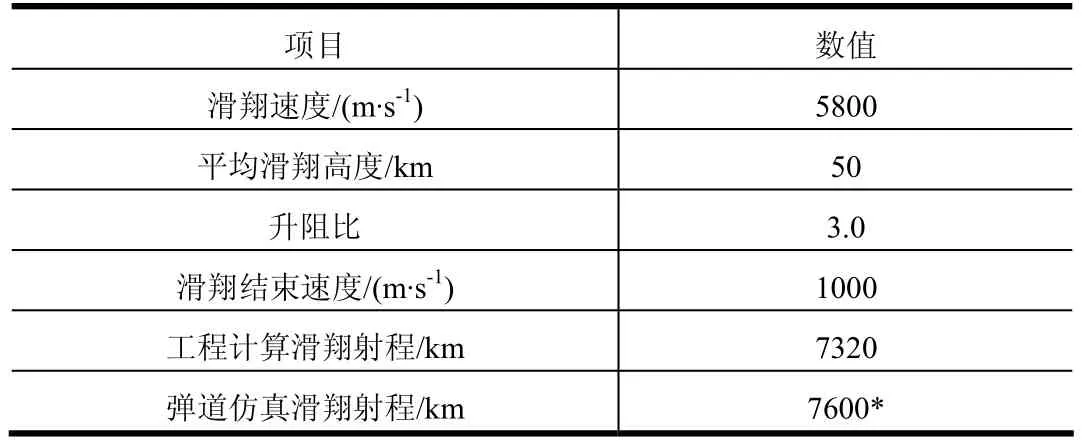
表1 平衡滑翔距离公式验证Tab.1 Validation of Equilibrium Glide’s Range Formula

从表1可以看出，平衡滑翔距离公式具有较好的计算精度，对于射程1000 km以上导弹的滑翔距离计算误差小于5%。

1.2 终端速度计算公式

将式（15）进一步转化，则有：

式（16）建立了滑翔终端速度与滑翔距离、滑翔高度的计算关系，已知滑翔飞行器当前高度、速度，即可计算出滑翔SL后的滑翔终端速度。

2 平衡滑翔弹道设计

由于大气密度ρ、重力加速度g是高度h的函数，速度V是马赫数Ma和高度h的函数，升力系数CL是马赫数Ma和攻角的函数，则由当前马赫数Ma和攻角即可解算出平衡机动高度指令，从而实现机动弹道设计。

平衡机动高度指令与马赫数和攻角的变化示意如图3所示。

图3 平衡机动高度指令示意Fig.3 Sketch Map of Equilibrium Glide’s Height Instruction

由图3可知，平衡滑翔弹道每一时刻升力和重力保持平衡，但由于不同飞行攻角对应的平衡滑翔弹道高度不同，滑翔同样射程后的速度损失也不同，利用这一特点可以开展终端速度控制与滑翔弹道联合设计。

3 基于终端速度约束的滑翔弹道设计

3.1 设计思路

利用不同滑翔高度气动阻力不同，滑翔距离一定情况下其滑翔终端速度也不同的特点，开展滑翔弹道和滑翔终端速度控制联合设计。利用弹上导航装置测量得到当前飞行速度，采用工程计算方法可以估计出一定滑翔距离后的滑翔终端速度，根据滑翔终端速度与标称速度之间的差异，进行当前弹道飞行高度的调节，通过增加或者降低气动阻力，实现对滑翔终端速度的调节。

3.2 设计方法

动态规划原理表明，过程中每一个节点达到最优即可实现全程的最优。借鉴该原理，在整个滑翔过程中实时进行滑翔终端速度控制。如图4所示，根据滑翔过程中当前速度、高度和飞行攻角，利用式（16）估算出滑翔终点速度，通过实时调节滑翔高度，实现对滑翔终端速度的控制。

图4 滑翔速度调节示意Fig.4 Sketch Map of Equilibrium Glide’s Velocity Adjustment

滑翔式飞行器在滑翔段根据高度指令形成过载指令进行导引飞行，其制导律为

式中cyN为过载指令；pK，dK为制导参数；h为导弹实时高度；ch为高度指令；h˙，ch˙为导弹实时高度和高度指令的时间导数。

速度调节最终需要落实到飞行高度的调节上，高度调节策略如下：

a）根据当前高度h0计算出平衡攻角αp和升阻比结合当前速度 V0和剩余滑翔射程 SL，根据式（16）计算出滑翔终端速度V，并与理想速度 VC对比，如果速度偏差满足要求（比如ΔV≤10 m/s），则不进行速度调节，反之则需要进行速度调节。

b）当速度偏差为正时需要进行减速调节。当平衡攻角pα小于最大升阻比攻角optα时，需要压低弹道；当平衡攻角pα大于最大升阻比攻角optα时，需要抬高弹道。给出高度变化量hΔ，使得在新的平衡高度和升阻比K1条件下的滑翔终端速度偏差ΔV满足要求，从而得到用于减速调节的平衡滑翔高度指令

c）当速度偏差为负时需要进行增速调节。当平衡攻角pα小于最大升阻比攻角optα时，需要抬高弹道；当平衡攻角pα大于最大升阻比攻角optα时，需要压低弹道。给出高度变化量hΔ，使得在新的平衡高度和升阻比K1条件下的滑翔终端速度偏差ΔV满足要求，从而得到用于增速调节的平衡滑翔高度指令

4 仿真算例

以滑翔射程2700 km、滑翔终端速度1500 m/s为约束，分别针对滑翔初始高度±1 km、滑翔初始速度±100 m/s、气动升力+20%、气动阻力-20%等拉偏情况，取终端速度控制偏差VΔ≤10 m/s，进行滑翔弹道和滑翔终端速度控制联合设计方法仿真验证，仿真结果如图5所示。

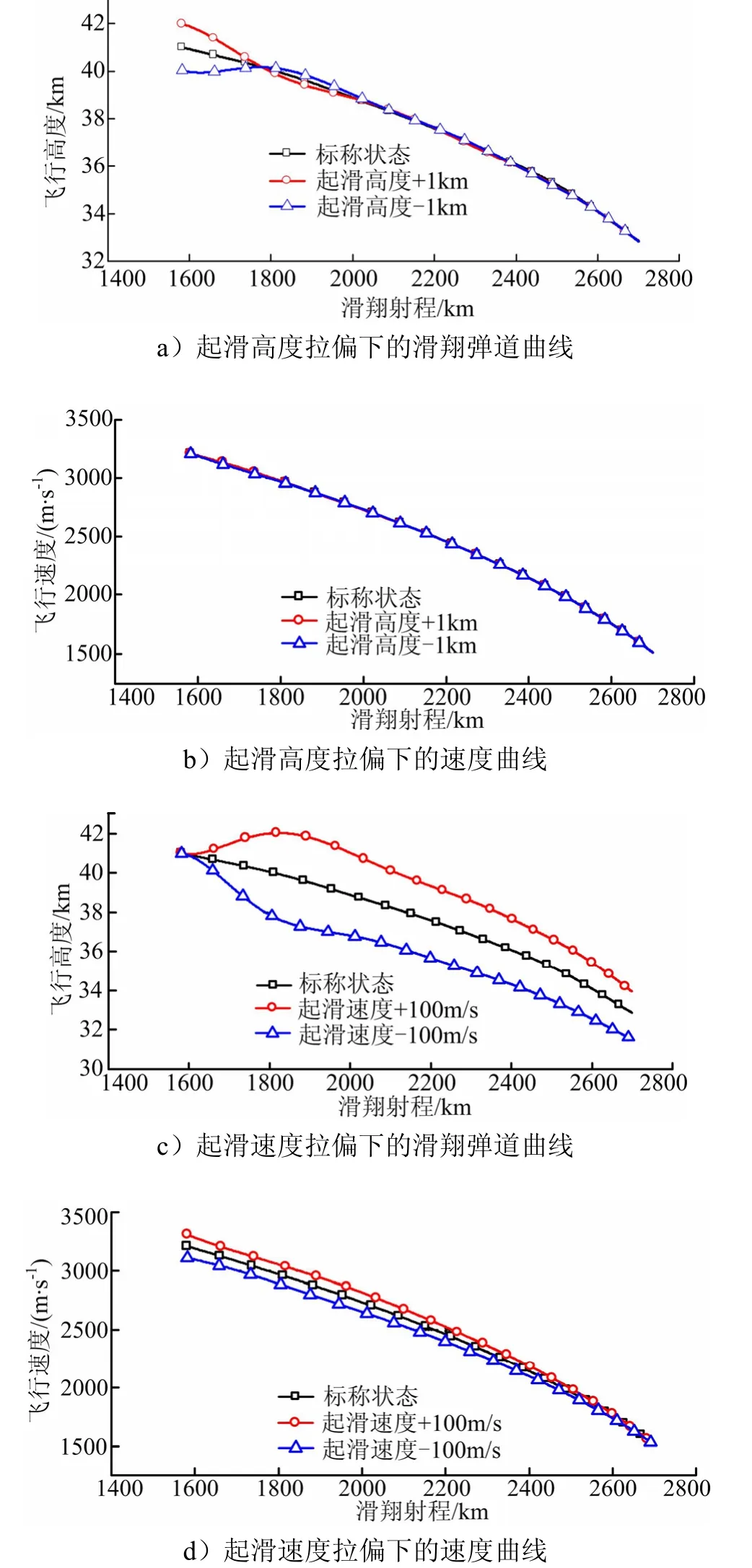
图5 偏差情况下滑翔弹道设计及终端速度控制曲线Fig.5 Gliding Trajectory Design and Terminal Velocity Control Effect when Errors Exist

续图5

从图5可看出，采用本文的联合设计方法，各种拉偏情况下终端速度控制情况良好，速度偏差在1 m/s范围之内。对于不同初始偏差，实时规划弹道存在不同的规律。起滑高度拉偏情况下，实时规划弹道初期采用小幅波动实现对终端速度的控制，最终基本与标称弹道吻合；起滑速度和气动系数拉偏情况下，为了抵消初始速度偏差及全程气动系数偏差带来的额外能量影响，需要全程抬高或压低弹道实现对终端速度的控制，拉偏弹道相比标称弹道存在小量的偏离（不大于4 km）。

可见，本文终端速度控制与滑翔弹道联合设计方法具有较好的应用效果，所设计的滑翔弹道平稳且具有良好的终端速度控制能力，对初始位置、速度偏差及气动偏差等具有较好的适应性，鲁棒性较强，具有较强的工程应用价值。