基于免疫克隆选择算法的爬升飞行方案优化设计

高 峰，李亚辉，师 娇，赵 洪，马奥家

（中国运载火箭技术研究院，北京，100076）

0 引 言

平飞俯冲击顶弹道是目前先进无人飞行器的典型攻击方式之一，可使飞行器从目标上方对较为薄弱的顶装甲进行攻击，增加毁伤效率。采用平飞俯冲击顶弹道时，首先需要使飞行器爬升至一定高度，然后转入定值高度平飞，满足转比条件时，按末制导律对目标进行俯冲攻击。爬升段弹道即飞行器起控开始爬升直至进入平飞前的一段弹道，其任务是使飞行器能够快速、稳定地爬升至平飞高度，并迅速地转入平飞段飞行，是保证飞行器完成对目标攻击的重要前提。由于飞行器在爬升段弹道的飞行过程中会受到爬升时间、爬升高度、可用攻角、导引头框架角等诸多因素制约，既要求飞行器在短时间内快速爬升至一定高度，又不能在爬升过程中丢失目标，因此需要对其进行优化设计，以提高飞行器的爬升效率，缩短爬升段的飞行时间，尽快进入理想战斗高度。为此，本文首先应用非均匀B样条（Non-uniform B-spline，NUBS）对无人飞行器爬升段的飞行控制方案进行了参数化处理，然后基于免疫克隆选择算法（Immune Clonal Selection Algorithm，ICSA）设计了爬升飞行方案优化流程，以爬升时间为主要优化目标进行了优化设计。

1 数学模型

1.1 问题描述

飞行器的爬升段弹道通常采用方案飞行，即按预定的飞行方案进行飞行，其中飞行方案是指设计弹道时所选定的某个运动参数随时间的变化规律[1]。通过初步分析易知，爬升时飞行器的弹道倾角与速度越大，飞行器到达平飞高度所需要的时间越小。但在实际的飞行过程当中，爬升时的弹道倾角与速度将受到失速攻角、导引头可用框架角等诸多因素的限制，且爬升时的弹道倾角越大，转入平飞的过渡时间越长。因此，爬升段弹道设计是一类复杂的非线性问题。

飞行器爬升段弹道优化设计的实质就是对所采用的飞行方案进行优化，即寻求一组最优的运动参数变化规律，使飞行器在满足各种约束条件的限制下，以最短时间爬升到指定高度转入平飞。

1.2 飞行运动模型

平飞俯冲击顶弹道的爬升段、平飞段以及末制导段是基于纵向平面内的弹道特征划分的，因此本文爬升飞行方案的优化设计也基于纵向平面。飞行器纵向平面内的运动方程[1]为

式中 m为质量；V为速度；t为时间；P为推力；α为攻角；X为阻力；g为重力加速度；θ为弹道倾角；Y为升力；为转动惯量；zω为俯仰角速度；zM为俯仰力矩；ϑ为俯仰角；x，y为飞行器质心位置坐标；为燃料质量秒流量；ε1，ε2为理想控制关系方程。

2 飞行方案参数化

爬升段飞行方案常用的运动参数控制规律包括俯仰角ϑ变化规律、攻角α变化规律以及弹道倾角θ变化规律等。目前弹上的攻角传感器与速度倾角传感器的精度并不是很理想，且成本较高。因此出于采用成熟技术、控制成本的角度考虑，无人飞行器的飞行方案采用俯仰角ϑ变化规律较为合适。式（1）中的理想控制关系式表示为

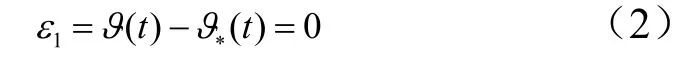
式中 ()tϑ为俯仰角ϑ随时间变化规律；()tϑ∗为给定的俯仰角ϑ变化规律。为保证在优化过程中对其进行准确描述以使效果达到最优，本文并未采用传统设计中常用的指数形式的变化规律，而是采用了计算机辅助几何设计中常用的非均匀B样条曲线[2,3]，其曲线方程可写为

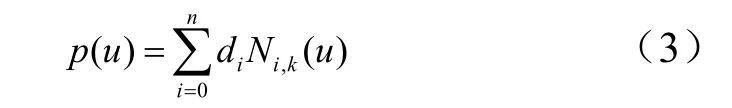
式中 lj为控制多边形的各边长，1,2,…,n)；L为总边长，

这样，通过NUBS将控制规律参数化，从而将对飞行方案优化转化为对NUBS优化，优化设计变量为NUBS的控制顶点

3 飞行方案优化设计

3.1 约束条件

在飞行器爬升过程中，如果在飞行过程中超出了可用框架角的范围，将导致导引头碰框并丢失目标；如果超出了临界攻角，将会导致飞行器升力急剧下降。因此，为保证飞行器在爬升段的正常飞行，应该对飞行过程中的框架角和攻角进行限定，约束条件为导引头框架角为导引头可用框架角）以及攻角为临界攻角）。一般在弹道优化中多采用罚函数法将约束问题转化为无约束优化问题进行考虑，但需要对惩罚因子进行设计。本文中根据罚函数法的基本原理，将约束条件转化为多目标优化问题中的两个目标1()gx和2()g x进行处理[4]，即：

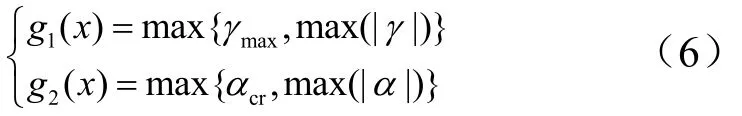
3.2 目标函数

飞行器爬升段的主要目的为爬升至指定高度，以及迅速完成爬升至平飞的过渡过程。因此，在爬升段结束时，飞行器应达到平飞高度，并满足平飞初始状态，一般主要指弹道倾角θ，在平飞时有lf0θ=。考虑到以上要求，本文目标函数取为飞行器爬升到平飞高度lfh后弹道倾角θ减小至0的所需时间T，综合式（6），目标函数 ()fx为

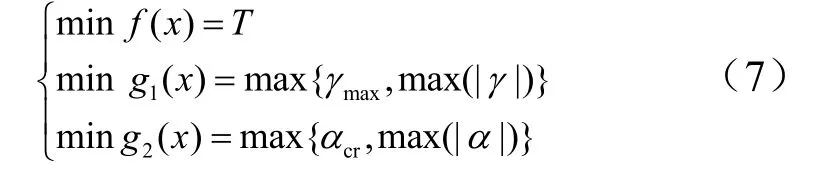
但应注意的是，虽然本文中将约束问题转化为多目标优化问题来处理，但与一般多目标优化问题的区别是，转化过来的目标函数在可行域内又退化成一个单目标优化问题 f(x)，此时有这样最终得到的是最优解而不是向着最优 Pareto-前端逼近的最优解集。

3.3 优化算法设计

ICSA是基于人工免疫系统（Artificial Immune Systems，AIS）的基本原理而提出的一种进化算法[4]。ICSA在收敛速度和多样性保持方面都有较好的效果，其核心步骤包括免疫克隆操作、免疫基因操作以及抗体更新操作等，其中免疫基因操作又包括克隆重组操作和克隆变异操作。

为提高优化效率，在本文的实际应用中，忽略了克隆重组操作。在克隆变异操作中，为防止算法出现类似于遗传算法早熟的现象，同时也能根据自身适应度值调整搜索范围，在本文中采用了将非一致性变异与自适应变异[5]相结合的方法。

在开始优化前，首先根据飞行力学模型进行初步弹道仿真，可有效缩小抗体向量的搜索空间，提高优化收敛速度。结合NUBS生成算法，将控制点作为抗体向量，得到基于ICSA的无人飞行器爬升飞行方案优化设计的步骤如图1所示，具体如下：

a）初始化飞行力学模型，进行初步弹道仿真，确定抗体向量的搜索空间；

b）给定抗体群规模N、平均克隆规模R、最大迭代次数maxg 、随机产生初代抗体群A；

c）用抗体向量所代表的控制顶点生成NUBS作为控制量，代入飞行器飞行力学模型进行解算，得到各抗体目标函数值；

d）根据抗体间亲和力确定克隆规模，对抗体群A进行克隆操作，得到抗体群1A；

e）运用非一致性变异与自适应变异组合方式对抗体群1A进行免疫克隆变异操作，得到抗体群2A；

f）根据步骤c计算抗体群2A各抗体目标函数值，

进行克隆选择操作，将抗体群2A划分为支配抗体群和非支配抗体群 Anon；

g）根据nonA 的目标函数值求解各抗体适应度值，进行抗体群更新操作，将非支配抗体群nonA 扩充（）或缩小（nonNN＜）为抗体群3A（），其中nonN 与3N分别为nonA 与3A的抗体群规模；

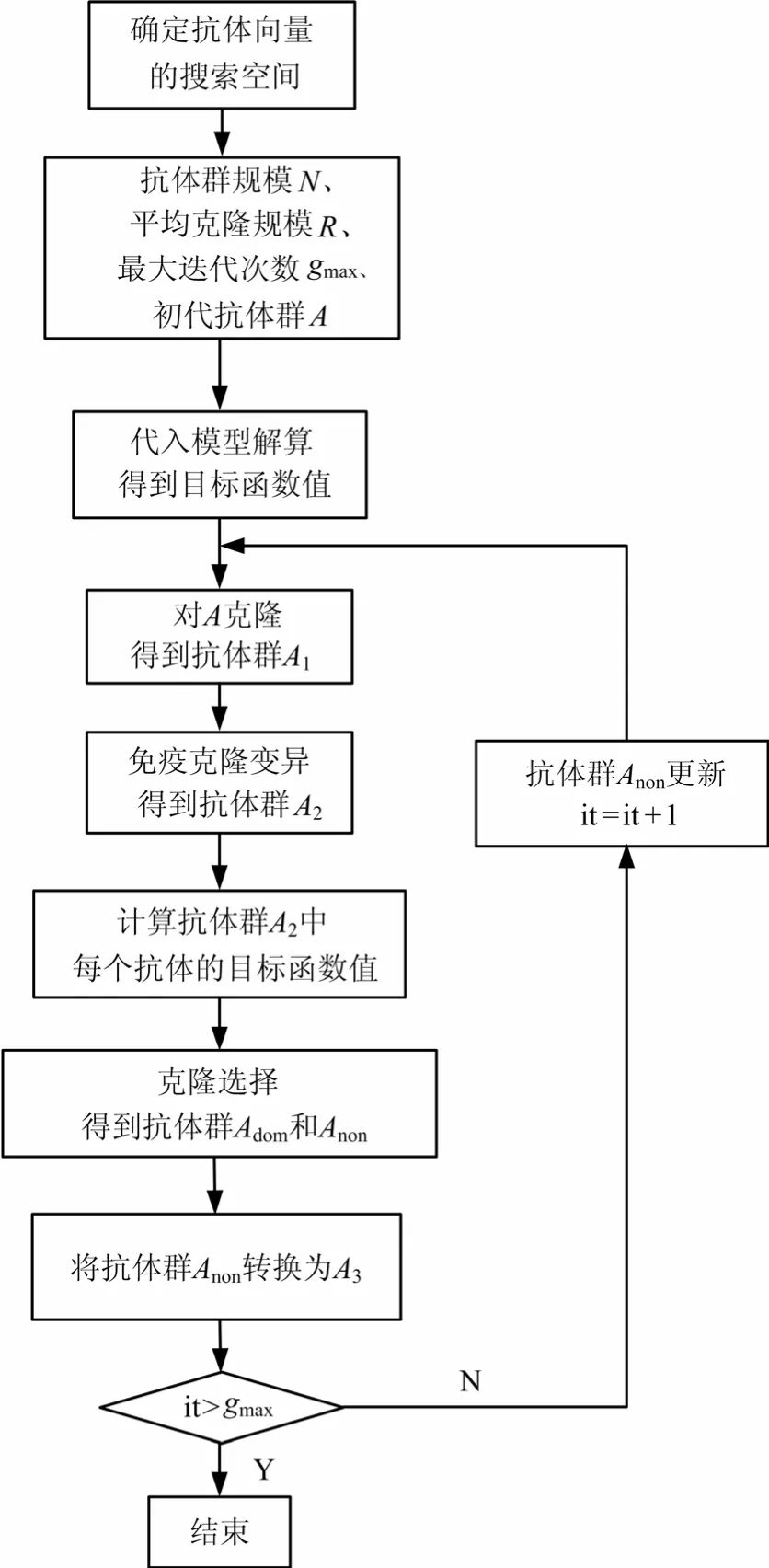
图1 基于ICSA的爬升飞行方案优化设计步骤Fig.1 Procedure of Climbing Flight Scheme Optimal Design Based on ICSA

4 仿真分析

根据图 1所示的优化设计步骤对无人飞行器的爬升飞行方案进行优化设计。在仿真过程中，将舵机简化为比例环节，稳定回路由姿态自动驾驶仪和弹体组成；设定理想平飞高度为150 m；飞行器的初始状态设定为：初始速度 16 m/s，初始射角 18°，启控时间0.3 s，导引头可用框架角限定为±25°，攻角限定条件设置为±15°；选用二次 NUBS，控制顶点id中，n=16；免疫克隆算法种群规模N=10，最大迭代次数爬升时间优化目标为不大于7 s；综合目标函数：

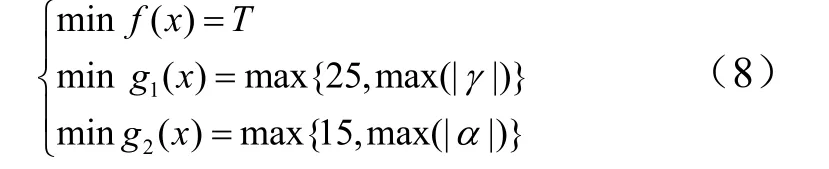
仿真结果如图2～8所示。

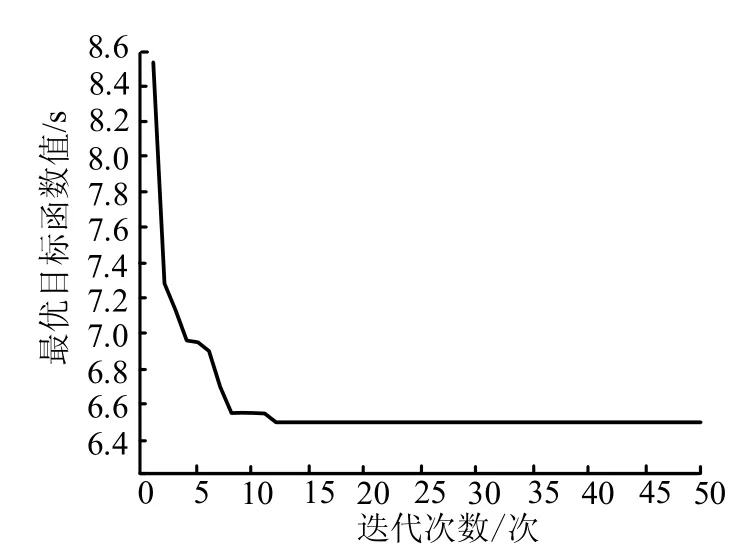
图2 最优目标函数值f（x）变化曲线Fig.2 Curve of Optimal Objective Function Value

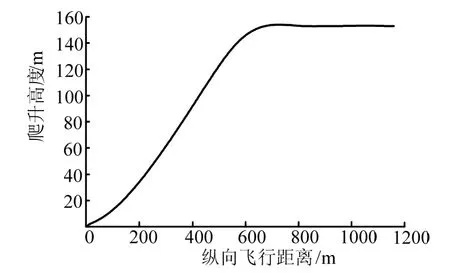
图3 优化后的爬升段弹道曲线Fig.3 Curve of Ascent Trajectory

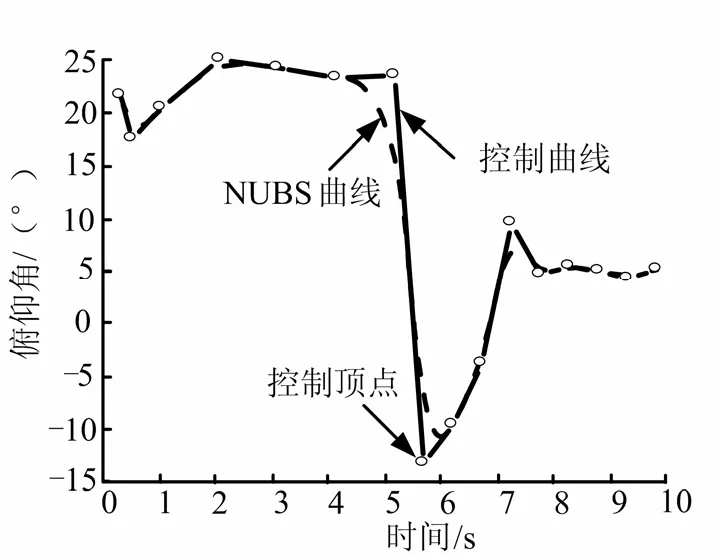
图4 控制顶点、控制曲线以及NUBS曲线Fig.4 Control Points of NUBS and NUBS Curve

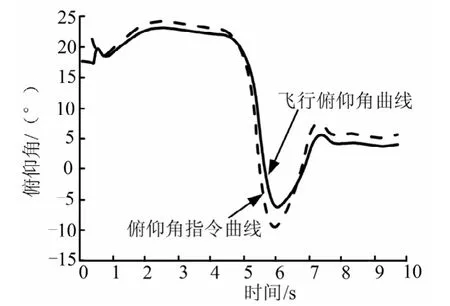
图5 俯仰角及控制指令曲线Fig.5 Curves of Pitch Angle and Control Law

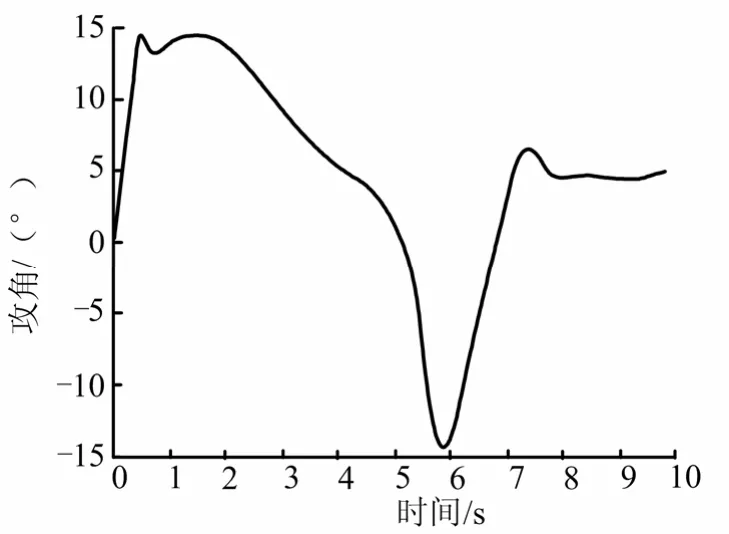
图6 攻角曲线Fig.6 Curve of Attack Angle

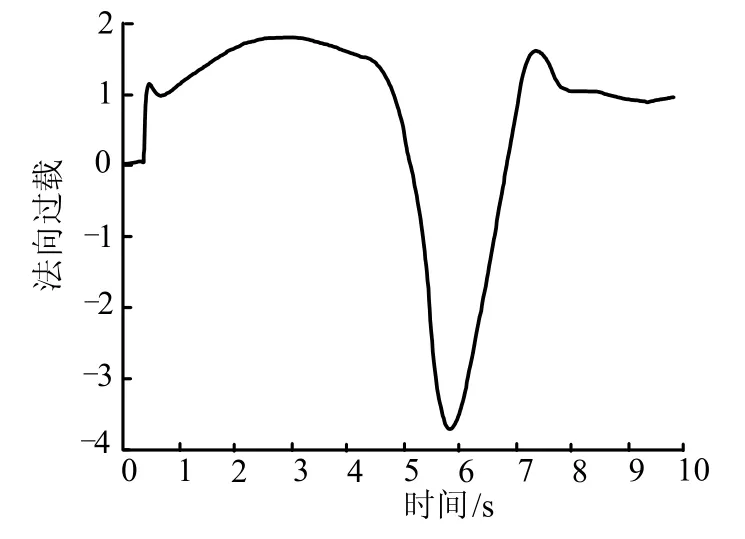
图7 法向过载曲线Fig.7 Curve of Normal Overload

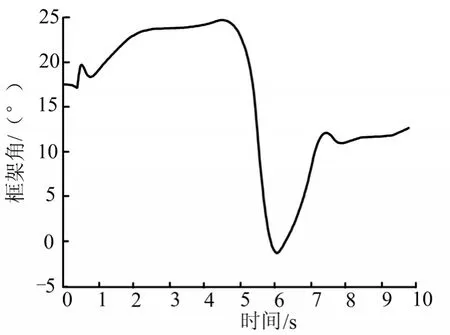
图8 框架角曲线Fig.8 Curve of Gimbal Angle

如图2所示，结合了非一致性变异及自适应变异的免疫克隆算法收敛速度较快，迭代开始后可迅速逼近最优值，且在第12次迭代就已经非常接近最优值。图3为优化后的爬升段弹道曲线，根据优化后的控制指令，飞行器不仅可以在6.5 s内爬升到指定高度，而且满足了导引头框架角的约束条件，在不丢失目标的情况下顺利地转入平飞。

图4为由控制顶点生成的NUBS曲线，由控制顶点联接成的多边形可以近似看作NUBS曲线的外接多边形。通过图5中俯仰角以及控制指令的对比可以看出俯仰角较好地跟踪了指令的变化，说明控制系统在设计指令下始终处于平稳可控的工作状态。

如图6及图7所示，在爬升初始阶段以及转平初始阶段，即在t=0.5～2 s以及t=5.7 s时，攻角非常接近临界攻角，法向过载绝对值也较大，说明飞行器在爬升段充分发挥了临界攻角所允许的机动性能。根据图8所示，框架角在爬升段全程均处于可用范围。

分析表明优化后的飞行方案较好地满足了飞行器对爬升段飞行方案的需求。同时优化方案简单清晰，具有较高的效率，对免疫克隆选择算法在其他飞行器设计领域的应用也具有一定的参考价值。

5 结 论

爬升段弹道的设计是弹道设计中的重要课题。本文结合无人飞行器爬升段采用的按俯仰角规律飞行方案，应用NUBS对飞行方案进行了参数化描述，采用ICSA进行了弹道优化设计，并根据实际应用设计了基于ICSA的无人飞行器爬升飞行方案优化流程。仿真结果表明优化后的飞行方案较好地满足了飞行器对爬升段弹道的需求。同时优化方案简单清晰，具有较高的效率，对免疫克隆算法应用在飞行器设计领域的其他方面也具有一定的参考价值。