高中空间向量学习解题技巧分析

马晓红

(江苏省苏州市田家炳实验高级中学 215000)

一、向量应用于空间几何解题

例1 在一个正三棱柱ABC-A1B1C1中，该三棱柱的棱长均为2，D为CC1的中点，求证：(Ⅰ)AB1⊥平面A1BD；(Ⅱ)求二面角A-A1D-B的大小.

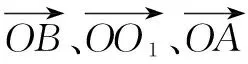
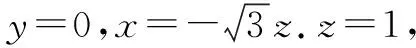
通过本次题目解答中，借助空间向量法知识点，能够有效地将空间几何解答，转换解题思维变换至代数问题，并且能够充分解决学生在解题过程中，所存在的想象力不足的问题.但是在此过程中教师必须重视在向量解题教学中，不能对学生灌输，向量知识对所有空间几何问题都能够解决的思想，以避免学生认为向量知识是万能的，走进解题思想误区.

二、向量应用于平面几何解题

例2 △ABC的顶点A(0，-4)，B(4,0)，C(-6,2)，BC、AB、AC的中点分别为D、E、F，求直线DE、EF、FD的方程.

由上解题案例可以发现，通过借助向量学习对高中数学平面几何问题解答过程中，能够借助更加科学合理的评价，从而对学生的良好学习习惯加以培养.并且能够借助学生本身的学习差异，在开展向量解题技巧教学过程中，创设公正的评析体系，由此有效确保学生的解题结果评价客观.

三、向量应用于不等式问题

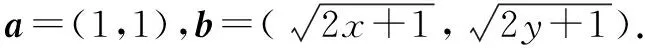
通过解答如上问题可以发现，通过针对此种不等式问题加以解决过程中，传统的解题方法已经无法适用.而通过向量解题技巧能够省略更多繁杂的计算步骤，减小计算量，有效节省传统计算所应当消耗的时间，同时还会提升整体计算正确率.

四、向量应用于三角函数问题

例4 求证cos(α-β)=sinαsinβ+cosαcosβ.

解设两个单位向量m=(cosα,sinα),n=(cosβ,sinβ),可见〈m,n〉=|α-β|.|m|=|n|=1.

基于坐标向量乘积公式可以得出：

m·n=sinαsinβ+cosαcosβ；

由于向量数量积公式可以得出：

m·n=cos(α-β).

通过联立可以发现cos(α-β)=sinαsinβ+cosαcosβ.

通过该题可以发现借助向量知识，在对三角函数有关问题加以解答，能够更好地将有关三角问题，借助较为简单的向量知识加以简化，从而有效提升学生本身的解题效率.

向量知识点作为高中数学知识的重要组成，同时向量知识点也可以被广泛运用于高中数学解题中，能够实现对数学解题的复杂问题简化，从而有效提高学生数学解题效率的同时，提高学生对向量知识点的应用能力.