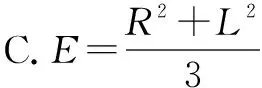灵活选择物理方法 巧解电场叠加问题
2018-08-15付同森
付同森
(广西南宁市第二中学 530029)
电场叠加是高考中的重点、难点、热点.电场叠加问题有多种题型和多种解法,最常见的有以下几种,本文对电场叠加问题解法进行归纳总结,便于学生掌握.
一、叠加法
叠加法就是把复杂的问题化为几种简单特殊典型情况,然后根据叠加原理进行叠加,求出复杂问题的结果.场的叠加遵循平行四边形定则.
例1 下列选项中的各1/4圆环大小相同如图1所示,所带电荷量已在图中标出,且电荷均匀分布,各1/4圆环间彼此绝缘.坐标原点O处电场强度最大的是( ).
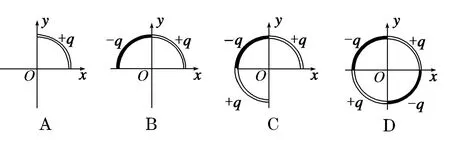
图1

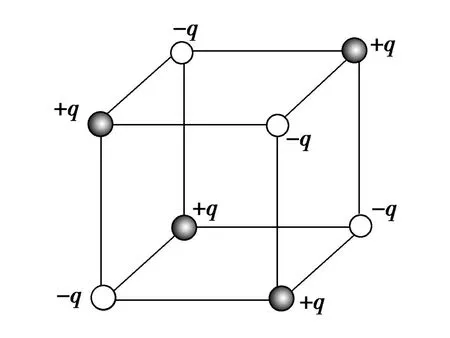
图2
例2 如图2所示,电量为+q和-q的点电荷分别位于正方体的顶点,正方体范围内电场强度为零的点有( ).
A.体中心、各面中心和各边中点
B.体中心和各边中点
C.各面中心和各边中点
D.体中心和各面中心
解析选D.由点电荷的场强公式和叠加法可知,各面顶点上的4个点电荷在所在面的中心的合场强为零.在正方体的上面的4个电荷在体中心产生的场强是零,下面的4个电荷在体中心产生的场强也是零,所以正方体的体中心合场强一定为零.由点电荷的场强公式和叠加法可知,各边中心的合场强不为零.选项D正确.

图3



图4

二、对称法
所谓对称法,就是从对称性的角度去分析物理过程,利用对称性解决物理问题的方法.利用对称性解题,往往无需冗长的数学推导过程,就能迅速准确地解决物理问题.
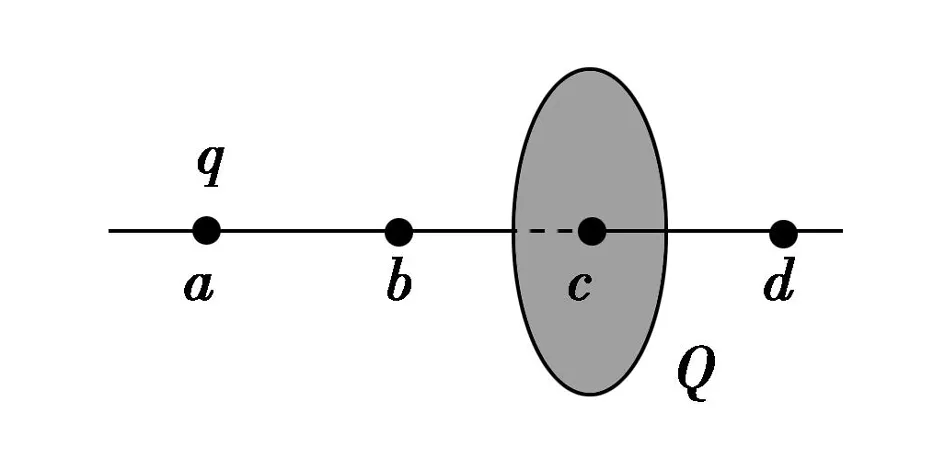
图5
例4 如图5所示,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则d点处场强的大小为(k为静电力常量)( ).

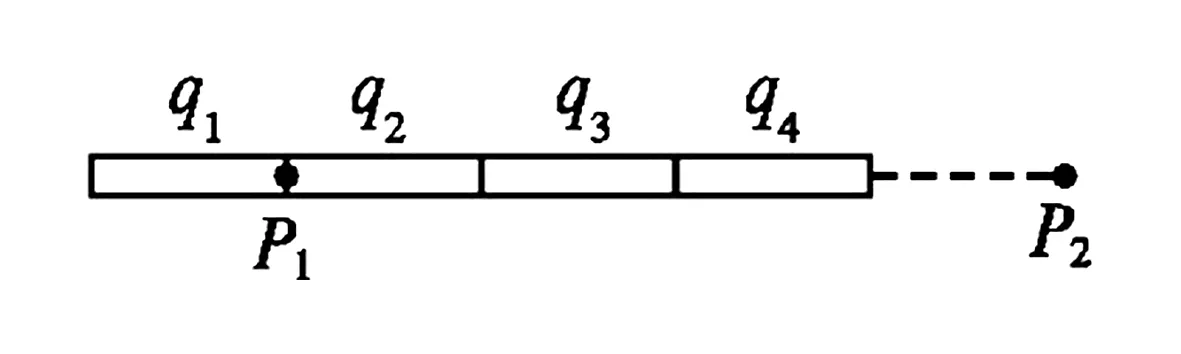
例5ab是长为l的均匀带电细杆如图6所示,P1、P2是位于ab所在直线上的两点,P1、P2的位置如图6所示.ab上电荷产生的静电场在P1处的场强大小为E1,在P2处的场强大小为E2,则以下说法正确的是( ).
A.两处的电场方向相同,E1>E2
B.两处的电场方向相反,E1>E2
C.两处的电场方向相同,E1 图6 解析选D.如图6所示由对称性可知,P1左端杆内l/4内的电荷与P1右端l/4内的电荷在P1处的场强为零,即P1处的场强E1是由杆的右端l/2内电荷在离P1的l/4处产生的.而P2处的场强E2可看做是整个杆l在杆的右端l/4的场强,故有E2>E1,由此分析可知,两处场强方向相反,故选项D正确. 在讨论物理问题时,往往因某些物理量分布的不对称使问题复杂化,在应用某些定理和公式直接求解时较为困难,补偿法就是使一些不对称分布问题假设在一定条件下变为对称分布,使一些定理或公式得以直接应用,使原来很复杂的问题简单化了,并很方便的求解,这种方法就是补偿法. 例6N(N>1)个电荷量均为q(q>0)的小球,均匀分布在半径为R的圆周上,示意如图7所示.若移去位于圆周上P点的一个小球,则圆心O点处的电场强度大小为____,方向____.(已知静电力常量为k) 图7 图7 例7 一个半径为R的绝缘球壳上均匀带有+Q的电荷,另一个电荷量为+q的电荷放在球心O上如图7所示,由于对称性,点电荷受力为0.现在球壳上挖去半径为r(r≪R)的一个小圆孔,则此时置于球心的点电荷所受的力的大小为____(已知静电力恒量为k),方向____. 图8 例8 如图8所示,A、B、C、D、E是半径为R的圆周上等间距的五个点,在这些点上除A点处外各固定一个点电荷,其电量均为+q,求圆心O处场强. 极限法是把某个物理量推向极端,从而作出科学的推理分析,给出判断或导出一般结论.该方法一般适用于题干中所涉及的物理量随条件单调变化的情况.极限法在进行某些物理过程分析时,具有独特作用,使问题化难为易,化繁为简,达到事半功倍的效果. 图9 例9 一半径为R的绝缘圆环上,均匀地带有电荷量为Q的电荷,在垂直于圆环平面的对称轴上有一点P,它与环心O的距离OP=L如图9所示.静电力常量为k,关于P点的场强E,下列四个表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( ). 图10 例10 如图所示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E的合理表达式应为( ). 解析选B.当x→∞时,应该有E→0.对于A项而言E=4πkσ(R1-R2)≠0,故A项错误;对D项而言E→4πkσ故D项错误;当x=0时,此时要求的场强为O点的场强,由对称性可知EO=0,对于C项而言,x=0时E为一定值,故C项错误.所以正确选项只能为B.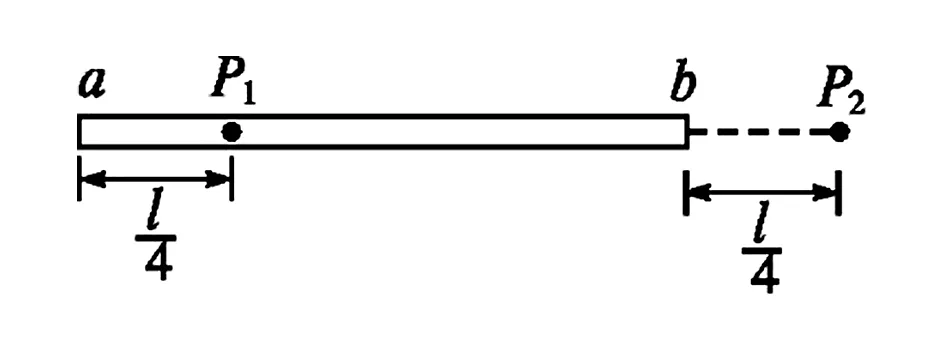
三、补偿法
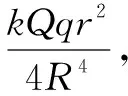

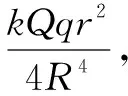



四、极限法