对一道竞赛题的拓展研究

陈 诚

(华中师范大学龙岗附属中学 518172)

著名数学教育家弗赖登塔尔认为：将数学作为一种活动来解释和分析，学习数学唯一正确的方法是让学生进行“再创造”，即数学知识应由学习者本人去发现和创造，教师的任务是帮助和引导学生进行“再创造”工作.基于以上认识，本文结合一道涉及椭圆的竞赛题，大胆尝试，多角度类比拓展研究，让学生的创造性与主动性得以充分展现.

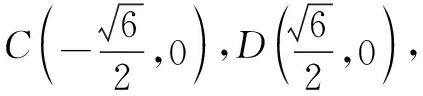
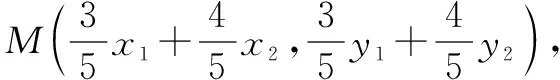
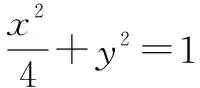
即为x1x2+4y1y2=0. ②

设AB:y=kx+m(k存在时)

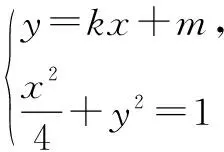
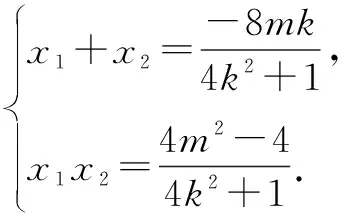
化简得:2m2=4k2+1. ③

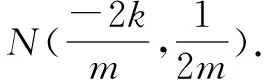
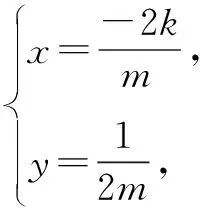
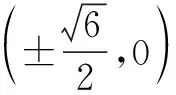
问题解决了，但对解法过程中进行拓展研究，发现留给我们的思考空间还很多.

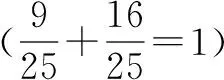
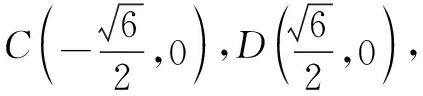
证明方法同上.

推广到更一般的情况:

解析几何是高考的重点、难点，学生感觉难的原因在于问题的转换以及运算的繁杂，要想提高学生的数学运算与数据处理的素养，必须充分发挥学生的主动性，激发学生的研究热情，让学生体会解析几何之美，让我们的运算变得快乐起来.同时,我们尽可能让一道题目变得更加丰满,知识容量更大,让学生的解题有研究的味道,让他们拥有”小科学家”的感觉,这样无论多么繁杂的问题学生有兴趣做下去.